2018年高考理数考前20天终极冲刺攻略+集合与常用逻辑用语
文档属性
| 名称 | 2018年高考理数考前20天终极冲刺攻略+集合与常用逻辑用语 |  | |
| 格式 | zip | ||
| 文件大小 | 324.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-26 07:25:49 | ||
图片预览


文档简介
核心考点解读——集合与常用逻辑用语
考纲解读里的I,II的含义如下:
I:对所列知识要知道其内容及含义,并能在有关问题中识别和直接使用,即了解和认识.
II:对所列知识要理解其确切含义及与其他知识的联系,能够进行叙述和解释,并能在实际问题的分析、综合、推理和判断等过程中运用,即理解和应用.(以下同)2·1·c·n·j·y
集合间的基本关系(II)
集合的交、并、补集的混合运算(II)
四种命题及其关系(I)
充分条件、必要条件(II)
简单的逻辑联结词(I)
全称量词与存在量词(II)
1.涉及本单元的题目一般考查集合间的基本关系及运算,四种命题及其关系,结合概念考查充分条件、必要条件及全称命题、特称命题的否定及真假的判断等.
2.从考查形式来看,涉及本单元知识的考题通常以选择题、填空题的形式出现,考查集合之间的关系以及概念、定理、公式的逻辑推理等.
3.从考查难度来看,考查集合的内容相对比较单一,试题难度相对容易,以通过解不等式,考查集合的运算为主,而常用逻辑用语则重点考查概念的理解及推理能力.
4.从考查热点来看,不等式的解法和概念、定理、公式之间的相互推理是本单元主要考查的内容,其要求不高,重在理解.
1.集合间的基本关系及运算
(1)理解子集、真子集的概念,知道由“若,有”得是的子集,记作;上述条件下,若“,”得是的真子集,记作.注意子集表示符号“”与元素和集合关系符号“”的区别.
(2)给定一个集合,能够写出其子集、真子集、非空子集的个数,如给定集合的元素个数为,则其子集、真子集、非空子集的个数分别为.
(3)交集:,取两个集合的公共元素组成集合;
并集:,取两个集合所有元素组成集合;
补集:,取全集中不属于集合A的元素组成集合.
注意集合的运算顺序,如表示先计算A的补集,再进行并集计算;则表示先进行A与B的并集计算,再进行补集计算.
2.四种命题及其关系
(1)能够根据给定命题写出其逆命题、否命题和逆否命题;
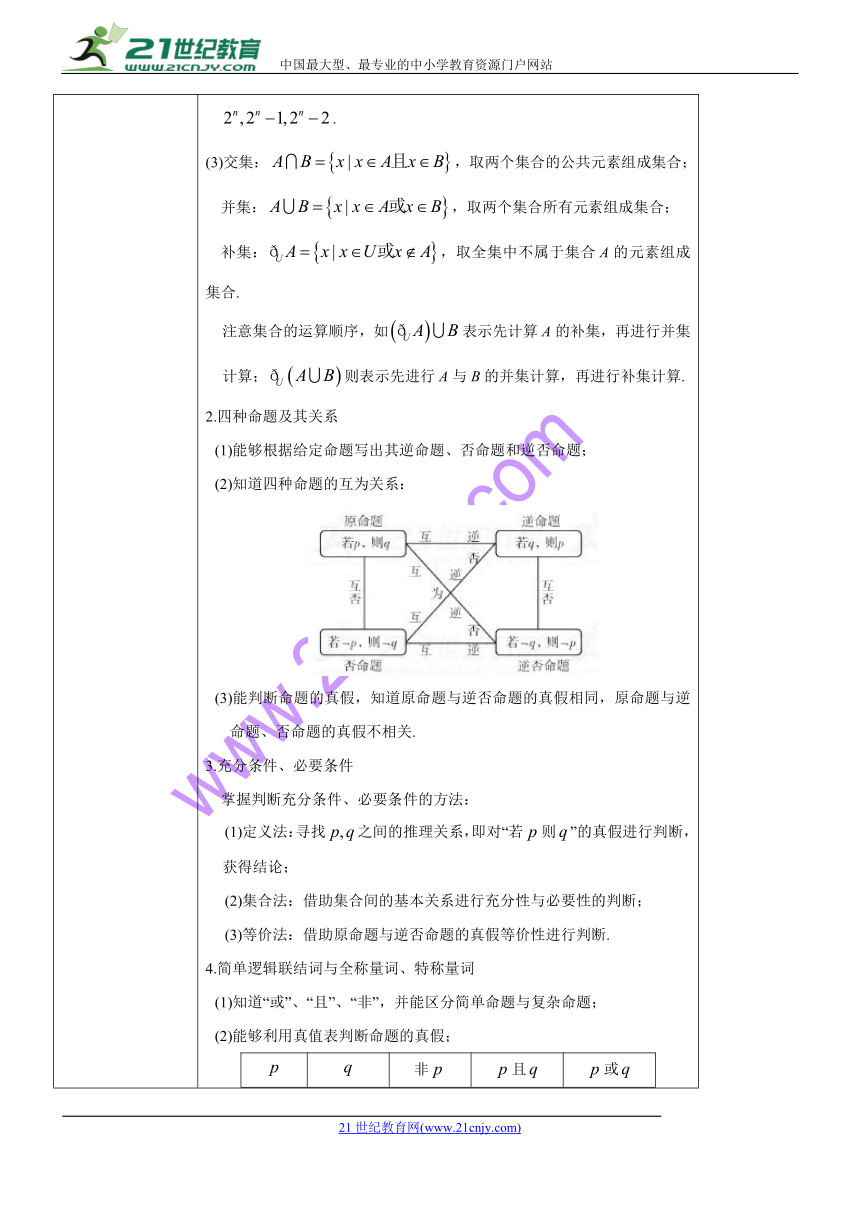
(2)知道四种命题的互为关系:
(3)能判断命题的真假,知道原命题与逆否命题的真假相同,原命题与逆命题、否命题的真假不相关.
3.充分条件、必要条件
掌握判断充分条件、必要条件的方法:
(1)定义法:寻找之间的推理关系,即对“若则”的真假进行判断,获得结论;
(2)集合法:借助集合间的基本关系进行充分性与必要性的判断;
(3)等价法:借助原命题与逆否命题的真假等价性进行判断.
4.简单逻辑联结词与全称量词、特称量词
(1)知道“或”、“且”、“非”,并能区分简单命题与复杂命题;
(2)能够利用真值表判断命题的真假;
非
且
或
真
真
假
真
真
真
假
假
假
真
假
真
真
假
真
假
假
真
假
假
(3)知道全称命题的否定是特称命题,特称命题的否定是全称命题;
(4)能够对全称命题、特称命题进行否定.
1.(2017高考新课标Ⅰ,理1)已知集合A={x|x<1},B={x|},则
A. B.
C. D.
2.(2017高考新课标II,理2)设集合,.若,则
A. B.
C. D.
3.(2017高考新课标III,理1)已知集合A=,B=,则AB中元素的个数为
A.3 B.2
C.1 D.0
4.(2016高考新课标Ⅱ,理2)已知集合,,则
A. B.
C. D.
5.(2016高考新课标I,理1)设集合 ,,则
A. B.
C. D.
6.(2017年高考浙江卷)已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4 + S6>2S5”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.(2016高考浙江,理4)命题“,使得”的否定形式是
A.,使得
B.,使得
C.,使得
D.,使得
8.(2015高考新课标I,理3)设命题:,则为
A. B.
C. D.
9.(2015高考新课标Ⅱ,理1)已知集合, ,则
A. B.
C. D.
1.已知集合,,则
A. B.
C. D.
2.已知全集,若集合, ,则
A. B.
C. D.
3.已知命题: ,;命题:,,则下列命题中为真命题的是
A. B.
C. D.
4.已知,集合,集合,若,则
A. B.
C. D.
5.下列命题中正确命题的个数是
①命题“若,则”的逆否命题为“若,则”;
②“”是“”的必要不充分条件;
③若为假命题,则,均为假命题;
④若命题:,,则:,.
A. B.
C. D.
1.设集合S={x|x>2},T={x|x2+3x4≤0},则=
A.(2,1] B.(∞,4]
C.(∞,1] D.[1,+∞)
2.设集合,,则
A. B.
C. D.
3.设命题p:>0,均有则为
A.>0,均有 B.使得
C.<0,均有 D.使得
4.已知直线l,m,其中只有m在平面α内,则“l∥α”是“l∥m”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件5.已知命题p1:y=2x2在R上为增函数;p2:y=2x+2在R上为减函数,则在命题q1:p1 p2,q2:p1 p2, q3:(p1) p2和q4:p1 (p2)中,真命题是21世纪教育网
A. q1,q3 B. q2,q3
C. q1,q4 D. q2,q4
真题回顾:1.A 2.C 3.B 4.C 5.D
6.C【解析】由,可知当时,有,即,反之,若,则,所以“d>0”是“S4 + S6>2S5”的充要条件,选C.21教育网
7.D 8.C 9A
名校预测
1.【答案】C 2.【答案】B 3.【答案】A
4.【答案】B【解析】因为,,且,所以或,
当时,,,不符合题意,舍去;当时,,,符合题意,
所以.故选B.
5.【答案】C【解析】①正确;对于②,由得且,则“”是“”的必要不充分条件,故②正确;对于③,若为假命题,则至少有一个为假命题,故③错误;④正确,故正确的是①②④.选C.21cnjy.com
专家押题
1. 【答案】C 2.【答案】B 3.【答案】D
4. 【答案】B【解析】当l∥α时,直线l与平面α内的直线m平行、异面都有可能,所以l∥m不成立;当l∥m时,又只有m在平面α内,根据直线与平面平行的判定定理知直线l∥α,即“l∥α”是“l∥m”的必要不充分条件,故选B.21·cn·jy·com
5. 【答案】C【解析】因为y=2x在R上为增函数,y=2在R上为减函数,所以y=2x2在R上为增函
数,y=2x+2在(∞,0]上为减函数,在(0,+∞)上为增函数,所以p1为真命题,p2为假命题,故q1: p1 p2为真命题;q2:p1 p2为假命题;q3:(p1) p2为假命题;q4:p1 (p2)为真命题.故真命题为q1和q4.故选C.www.21-cn-jy.com
考纲解读里的I,II的含义如下:
I:对所列知识要知道其内容及含义,并能在有关问题中识别和直接使用,即了解和认识.
II:对所列知识要理解其确切含义及与其他知识的联系,能够进行叙述和解释,并能在实际问题的分析、综合、推理和判断等过程中运用,即理解和应用.(以下同)2·1·c·n·j·y
集合间的基本关系(II)
集合的交、并、补集的混合运算(II)
四种命题及其关系(I)
充分条件、必要条件(II)
简单的逻辑联结词(I)
全称量词与存在量词(II)
1.涉及本单元的题目一般考查集合间的基本关系及运算,四种命题及其关系,结合概念考查充分条件、必要条件及全称命题、特称命题的否定及真假的判断等.
2.从考查形式来看,涉及本单元知识的考题通常以选择题、填空题的形式出现,考查集合之间的关系以及概念、定理、公式的逻辑推理等.
3.从考查难度来看,考查集合的内容相对比较单一,试题难度相对容易,以通过解不等式,考查集合的运算为主,而常用逻辑用语则重点考查概念的理解及推理能力.
4.从考查热点来看,不等式的解法和概念、定理、公式之间的相互推理是本单元主要考查的内容,其要求不高,重在理解.
1.集合间的基本关系及运算
(1)理解子集、真子集的概念,知道由“若,有”得是的子集,记作;上述条件下,若“,”得是的真子集,记作.注意子集表示符号“”与元素和集合关系符号“”的区别.
(2)给定一个集合,能够写出其子集、真子集、非空子集的个数,如给定集合的元素个数为,则其子集、真子集、非空子集的个数分别为.
(3)交集:,取两个集合的公共元素组成集合;
并集:,取两个集合所有元素组成集合;
补集:,取全集中不属于集合A的元素组成集合.
注意集合的运算顺序,如表示先计算A的补集,再进行并集计算;则表示先进行A与B的并集计算,再进行补集计算.
2.四种命题及其关系
(1)能够根据给定命题写出其逆命题、否命题和逆否命题;
(2)知道四种命题的互为关系:
(3)能判断命题的真假,知道原命题与逆否命题的真假相同,原命题与逆命题、否命题的真假不相关.
3.充分条件、必要条件
掌握判断充分条件、必要条件的方法:
(1)定义法:寻找之间的推理关系,即对“若则”的真假进行判断,获得结论;
(2)集合法:借助集合间的基本关系进行充分性与必要性的判断;
(3)等价法:借助原命题与逆否命题的真假等价性进行判断.
4.简单逻辑联结词与全称量词、特称量词
(1)知道“或”、“且”、“非”,并能区分简单命题与复杂命题;
(2)能够利用真值表判断命题的真假;
非
且
或
真
真
假
真
真
真
假
假
假
真
假
真
真
假
真
假
假
真
假
假
(3)知道全称命题的否定是特称命题,特称命题的否定是全称命题;
(4)能够对全称命题、特称命题进行否定.
1.(2017高考新课标Ⅰ,理1)已知集合A={x|x<1},B={x|},则
A. B.
C. D.
2.(2017高考新课标II,理2)设集合,.若,则
A. B.
C. D.
3.(2017高考新课标III,理1)已知集合A=,B=,则AB中元素的个数为
A.3 B.2
C.1 D.0
4.(2016高考新课标Ⅱ,理2)已知集合,,则
A. B.
C. D.
5.(2016高考新课标I,理1)设集合 ,,则
A. B.
C. D.
6.(2017年高考浙江卷)已知等差数列{an}的公差为d,前n项和为Sn,则“d>0”是“S4 + S6>2S5”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.(2016高考浙江,理4)命题“,使得”的否定形式是
A.,使得
B.,使得
C.,使得
D.,使得
8.(2015高考新课标I,理3)设命题:,则为
A. B.
C. D.
9.(2015高考新课标Ⅱ,理1)已知集合, ,则
A. B.
C. D.
1.已知集合,,则
A. B.
C. D.
2.已知全集,若集合, ,则
A. B.
C. D.
3.已知命题: ,;命题:,,则下列命题中为真命题的是
A. B.
C. D.
4.已知,集合,集合,若,则
A. B.
C. D.
5.下列命题中正确命题的个数是
①命题“若,则”的逆否命题为“若,则”;
②“”是“”的必要不充分条件;
③若为假命题,则,均为假命题;
④若命题:,,则:,.
A. B.
C. D.
1.设集合S={x|x>2},T={x|x2+3x4≤0},则=
A.(2,1] B.(∞,4]
C.(∞,1] D.[1,+∞)
2.设集合,,则
A. B.
C. D.
3.设命题p:>0,均有则为
A.>0,均有 B.使得
C.<0,均有 D.使得
4.已知直线l,m,其中只有m在平面α内,则“l∥α”是“l∥m”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件5.已知命题p1:y=2x2在R上为增函数;p2:y=2x+2在R上为减函数,则在命题q1:p1 p2,q2:p1 p2, q3:(p1) p2和q4:p1 (p2)中,真命题是21世纪教育网
A. q1,q3 B. q2,q3
C. q1,q4 D. q2,q4
真题回顾:1.A 2.C 3.B 4.C 5.D
6.C【解析】由,可知当时,有,即,反之,若,则,所以“d>0”是“S4 + S6>2S5”的充要条件,选C.21教育网
7.D 8.C 9A
名校预测
1.【答案】C 2.【答案】B 3.【答案】A
4.【答案】B【解析】因为,,且,所以或,
当时,,,不符合题意,舍去;当时,,,符合题意,
所以.故选B.
5.【答案】C【解析】①正确;对于②,由得且,则“”是“”的必要不充分条件,故②正确;对于③,若为假命题,则至少有一个为假命题,故③错误;④正确,故正确的是①②④.选C.21cnjy.com
专家押题
1. 【答案】C 2.【答案】B 3.【答案】D
4. 【答案】B【解析】当l∥α时,直线l与平面α内的直线m平行、异面都有可能,所以l∥m不成立;当l∥m时,又只有m在平面α内,根据直线与平面平行的判定定理知直线l∥α,即“l∥α”是“l∥m”的必要不充分条件,故选B.21·cn·jy·com
5. 【答案】C【解析】因为y=2x在R上为增函数,y=2在R上为减函数,所以y=2x2在R上为增函
数,y=2x+2在(∞,0]上为减函数,在(0,+∞)上为增函数,所以p1为真命题,p2为假命题,故q1: p1 p2为真命题;q2:p1 p2为假命题;q3:(p1) p2为假命题;q4:p1 (p2)为真命题.故真命题为q1和q4.故选C.www.21-cn-jy.com
同课章节目录
