2018年高考理数考前20天终极冲刺攻略+空间几何体
文档属性
| 名称 | 2018年高考理数考前20天终极冲刺攻略+空间几何体 |

|
|
| 格式 | zip | ||
| 文件大小 | 666.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-26 00:00:00 | ||
图片预览



文档简介
核心考点解读——空间几何体
空间几何体的三视图与直观图(II)
空间几何体的表面积、体积(I)
球的表面积、体积(I)
根据三视图求空间几何体的表面积、体积(II)
1.从考查题型来看,涉及本知识点的题目一般以选择题、填空题的形式出现,
考查空间几何体的三视图的识别,空间几何体的表面积、体积的计算.
2.从考查内容来看,主要考查由空间几何体的三视图确定其直观图,并求其表面积、体积.重点在于空间几何体的表面积、体积计算公式的正确使用,难点是如何根据三视图确定空间几何体的结构特征.
3.从考查热点来看,空间几何体的表面积、体积问题是高考命题的热点,以空间几何体的三视图为基准,识别该几何体,并计算其表面积、体积,通常情况下以计算体积为主,这是高考主要的考查方式.
1.空间几何体的三视图、直观图
(1)空间几何体的三视图:正视图、侧视图、俯视图,其特点是从空间几何体的正面、左面、上面用平行投影的方法来得到相应的视图,其处理原则是 “长对正、宽相等,高平齐”.
(2)由三视图画空间几何体的直观图时,可以先根据俯视图确定几何体的底面,然后根据正视图和侧视图确定空间几何体的的形状,并根据斜二测画法画出空间几何体.注意可见的轮廓线画成实线,存在但不可见的轮廓线画成虚线.
2.空间几何体的表面积、体积问题
(1)空间几何体的表面积的计算方式是:
i)若是多面体,则分别计算每个面的面积,然后相加即得表面积;
ii)若是旋转体,则将侧面的曲面进行展开,计算其面积,再加上底面面积,即得表面积.
(2)柱体、锥体、台体的体积计算公式(为底面面积,为高):
,,.
3.球的表面积、体积(为球的半径):
(1)球的表面积:.
(2)球的体积:.
(3)球的表面积与体积由球的半径唯一确定,若球的半径扩大或缩小倍,则其相应的表面积、体积也扩大或缩小倍和倍.
(4)球的表面积、体积问题常与其他空间几何体相结合出题,比如求给定空间几何体的外接球或内切球的表面积、体积时,要根据该几何体的特点确定外接球或内切球的半径,以此求得相应的值.
4.根据三视图求简单几何体或组合体的表面积、体积
解决与三视图有关的简单几何体或组合体的表面积、体积问题时,首先要根据三视图确定简单几何体或组合体的形状,若是简单几何体,则只需根据相应的表面积、体积计算公式计算即可;若是组合体,常将组合体割补为几个简单的几何体进行求解.求解时注意还原的准确性和数据的准确性.
长方体或正方体是研究三视图的最好的母体,通常可以借助长方体或正方体,通过切割、挖空等手段确定几何体的结构特征.
1.(2017高考新课标Ⅰ,理7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为21·世纪*教育网
A.10 B.12
C.14 D.16
2.(2017高考新课标Ⅱ,理4)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为2-1-c-n-j-y
A. B.
C. D.
3.(2017高考新课标Ⅲ,理8)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为21*cnjy*com
A. B.
C. D.
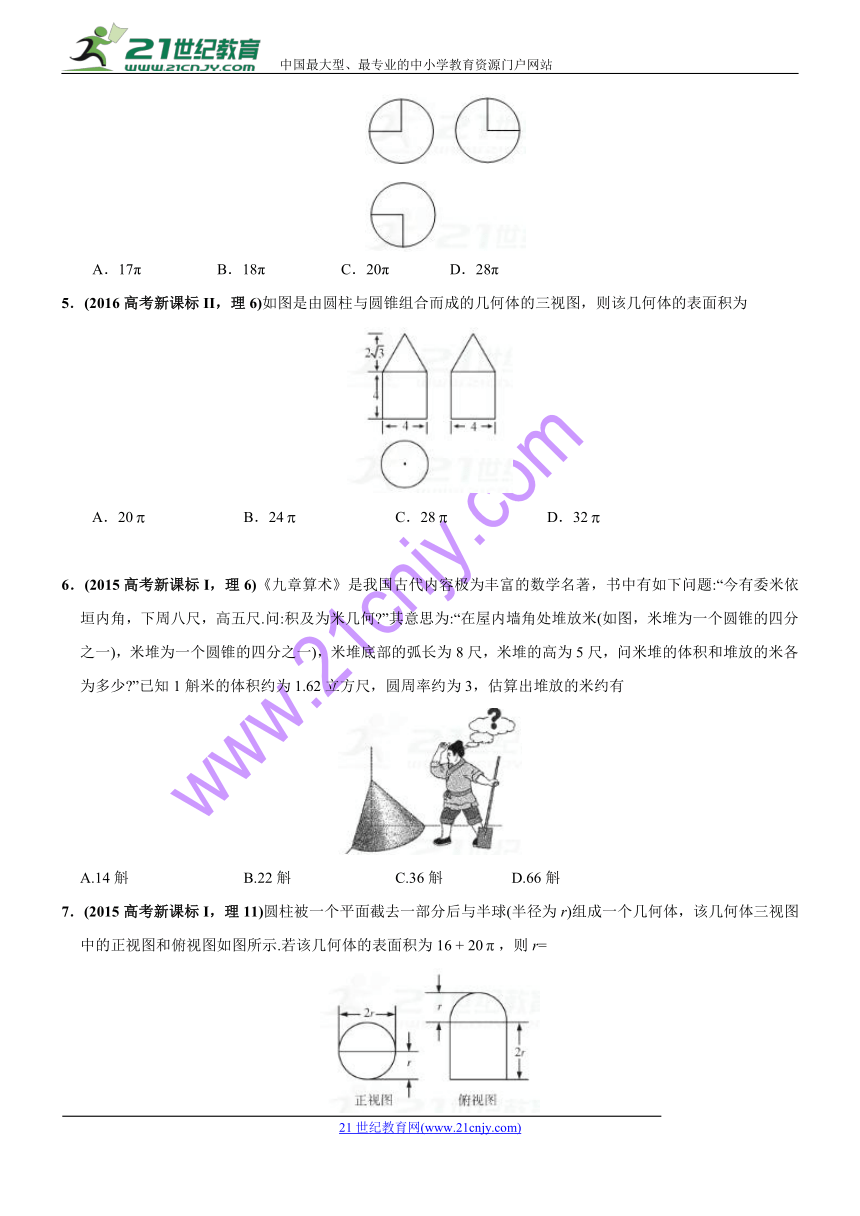
4.(2016高考新课标I,理6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是【21cnj*y.co*m】
A.17π B.18π C.20π D.28π 【21教育名师】
5.(2016高考新课标II,理6)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为
A.20 B.24 C.28 D.32
6.(2015高考新课标I,理6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有21·cn·jy·com
A.14斛 B.22斛 C.36斛 D.66斛
7.(2015高考新课标I,理11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20,则r=
A.1 B.2 C.4 D.8
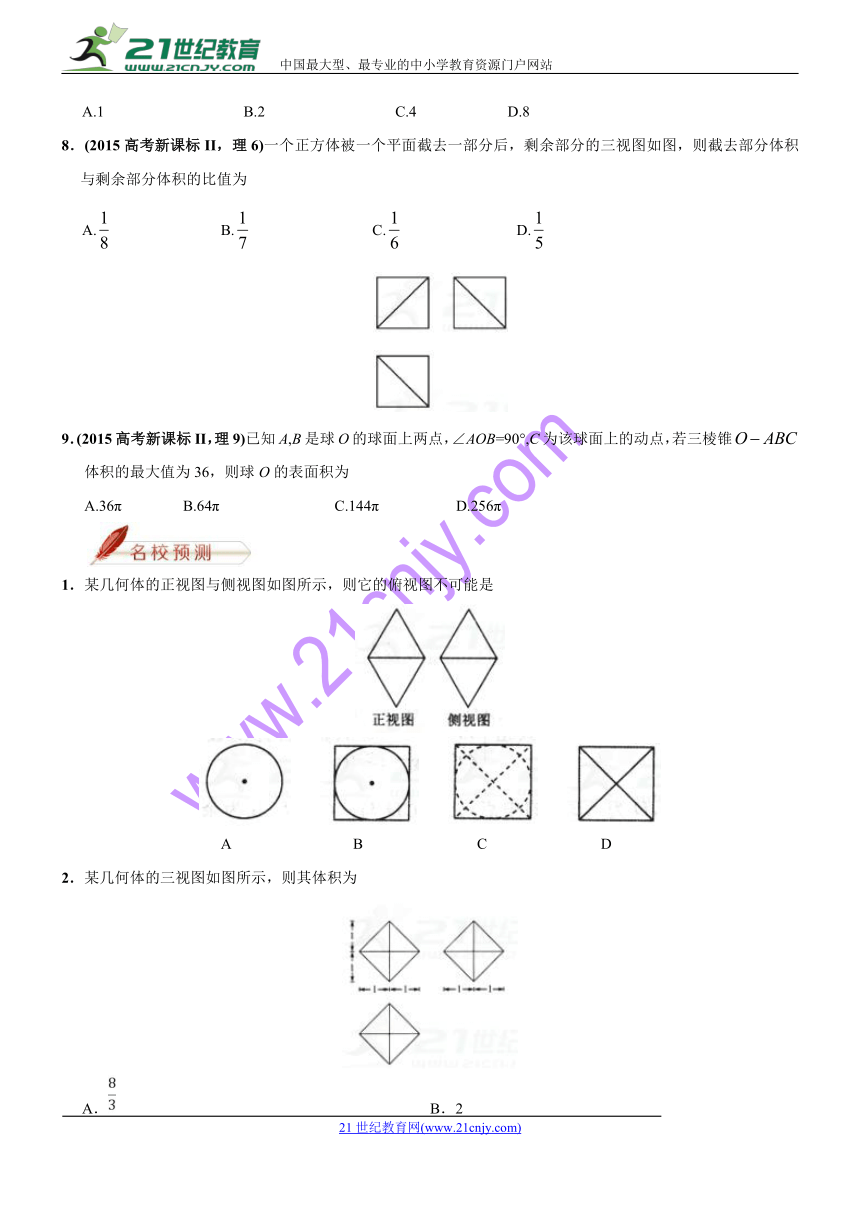
8.(2015高考新课标II,理6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为
A. B. C. D.
9.(2015高考新课标II,理9)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥体积的最大值为36,则球O的表面积为2·1·c·n·j·y
A.36π B.64π C.144π D.256π
1.某几何体的正视图与侧视图如图所示,则它的俯视图不可能是
A B C D www-2-1-cnjy-com
2.某几何体的三视图如图所示,则其体积为
A. B.2
C. D.
3.《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马,其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上,则该球的体积为【21教育】
A. B.
C. D.
4.已知三棱锥的外接球的球心恰好是线段的中点,且,则三棱锥的体积为
A. B.
C. D.
5.如图,在底面为矩形的四棱锥中,平面,,分别为棱,上一点,已知,,,且平面,四面体的每个顶点都在球的表面上,则球的表面积为
A. B.
C. D.
1.《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽丈,长丈;上棱长丈,无宽,高丈(如图).问它的体积是多少? ”这个问题的答案是21教育网
A. 立方丈 B. 立方丈
C. 立方丈 D. 立方丈
2.如图是一个空间几何体的三视图,其中正视图上半部分是一个底面边长为4、高为1的等腰三角形,正视图下半部分是一个边长为2的正方形,则该空间几何体的体积是21cnjy.com
A. B.
C. D.
3.点A,B,C,D均在同一球面上,且AB,AC,AD两两垂直,且, ,则该球的表面积为
A. B. C. D.
真题回顾:
1.B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为,故选B.【21·世纪·教育·网】
2.B【解析】由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积,上半部分是一个底面半径为3,高为6的圆柱的一半,其体积,故该组合体的体积.故选B.
3.B【解析】绘制圆柱的轴截面如图所示:由题意可得:,
结合勾股定理,底面半径,由圆柱的体积公式,可得圆柱的体积是,故选B.
4.A 【解析】由三视图知,该几何体的直观图如图所示:
是一个球被切掉左上角的,即该几何体是个球,设球的半径为,则,解得,所以它的表面积是的球面面积和三个扇形面积之和,即,故选A.
5.C【解析】由题意可知,圆柱的侧面积为,圆锥的侧面积为,圆柱的底面面积为,故该几何体的表面积为,故选C.
【名师点睛】由三视图还原几何体的方法:
6.B【解析】设圆锥底面半径为r,则 ,所以米堆的体积为 故堆放的米约为 故选B.
7.B【解析】由正视图和俯视图知,截圆柱的平面过圆柱的轴线,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r,圆柱的高为2r,其表面积为==16 + 20,解得r=2,故选B.21世纪教育网
8.D【解析】由三视图得,在正方体中,截去四面体,如图所示,设正方体棱长为,则,故剩余几何体的体积为,所以截去部分体积与剩余部分体积的比值为,故选D.21*教*育*名*师
9.C【解析】如图,当点C位于垂直于面的直径端点时,三棱锥的体积最大,设球的半径为,此时,故,则球的表面积为,故选C.
名校预测
1.【答案】C【解析】若几何体为两个圆锥体的组合体,则俯视图为A;若几何体为四棱锥与圆锥的组合体,则俯视图为B;若几何体为两个四棱锥的组合体,则俯视图为D;不可能为C,故选C.
2.【答案】C【解析】由三视图可知,该几何体为正八面体,即两个全等的正四棱锥,棱长为,高为,
所以其体积为,故选C.
3.【答案】C【解析】如图所示,该几何体为四棱锥.底面为矩形,其中底面,
.则该阳马的外接球的直径为∴该阳马的外接球的体积=故选C.
4.【答案】A【解析】因为三棱锥的外接球的球心恰好是线段的中点,所以为直角三角形,又,则为等腰直角三角形,21-cnjy*com
则,且,则平面,
所以.故选A.
5.【答案】C【解析】如图,在棱CD上取一点H,使得HD=1,平面BCE,
又平面BCE,平面平面BCE,又平面平面ABCD=GH,平面平面ABCD=BC,= HD=1,故四面体可以补成一个长方体,且长,宽,高分别为4,1,1,故球的表面积为 www.21-cn-jy.com
专家押题
1.【答案】A【解析】过点分别作平面和平面 垂直于底面,所以几何体的体积分为三部分中间是直三棱柱,两边是两个一样的四棱锥,所以立方丈,故选A.
2.【答案】B【解析】由三视图可知,几何体的上半部分为圆锥,下半部分为圆柱,故体积为.故选B.
3.【答案】B【解析】三棱锥的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,,它的外接球半径是,外接球的表面积是4π()2=14π.
空间几何体的三视图与直观图(II)
空间几何体的表面积、体积(I)
球的表面积、体积(I)
根据三视图求空间几何体的表面积、体积(II)
1.从考查题型来看,涉及本知识点的题目一般以选择题、填空题的形式出现,
考查空间几何体的三视图的识别,空间几何体的表面积、体积的计算.
2.从考查内容来看,主要考查由空间几何体的三视图确定其直观图,并求其表面积、体积.重点在于空间几何体的表面积、体积计算公式的正确使用,难点是如何根据三视图确定空间几何体的结构特征.
3.从考查热点来看,空间几何体的表面积、体积问题是高考命题的热点,以空间几何体的三视图为基准,识别该几何体,并计算其表面积、体积,通常情况下以计算体积为主,这是高考主要的考查方式.
1.空间几何体的三视图、直观图
(1)空间几何体的三视图:正视图、侧视图、俯视图,其特点是从空间几何体的正面、左面、上面用平行投影的方法来得到相应的视图,其处理原则是 “长对正、宽相等,高平齐”.
(2)由三视图画空间几何体的直观图时,可以先根据俯视图确定几何体的底面,然后根据正视图和侧视图确定空间几何体的的形状,并根据斜二测画法画出空间几何体.注意可见的轮廓线画成实线,存在但不可见的轮廓线画成虚线.
2.空间几何体的表面积、体积问题
(1)空间几何体的表面积的计算方式是:
i)若是多面体,则分别计算每个面的面积,然后相加即得表面积;
ii)若是旋转体,则将侧面的曲面进行展开,计算其面积,再加上底面面积,即得表面积.
(2)柱体、锥体、台体的体积计算公式(为底面面积,为高):
,,.
3.球的表面积、体积(为球的半径):
(1)球的表面积:.
(2)球的体积:.
(3)球的表面积与体积由球的半径唯一确定,若球的半径扩大或缩小倍,则其相应的表面积、体积也扩大或缩小倍和倍.
(4)球的表面积、体积问题常与其他空间几何体相结合出题,比如求给定空间几何体的外接球或内切球的表面积、体积时,要根据该几何体的特点确定外接球或内切球的半径,以此求得相应的值.
4.根据三视图求简单几何体或组合体的表面积、体积
解决与三视图有关的简单几何体或组合体的表面积、体积问题时,首先要根据三视图确定简单几何体或组合体的形状,若是简单几何体,则只需根据相应的表面积、体积计算公式计算即可;若是组合体,常将组合体割补为几个简单的几何体进行求解.求解时注意还原的准确性和数据的准确性.
长方体或正方体是研究三视图的最好的母体,通常可以借助长方体或正方体,通过切割、挖空等手段确定几何体的结构特征.
1.(2017高考新课标Ⅰ,理7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形,这些梯形的面积之和为21·世纪*教育网
A.10 B.12
C.14 D.16
2.(2017高考新课标Ⅱ,理4)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为2-1-c-n-j-y
A. B.
C. D.
3.(2017高考新课标Ⅲ,理8)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为21*cnjy*com
A. B.
C. D.
4.(2016高考新课标I,理6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是【21cnj*y.co*m】
A.17π B.18π C.20π D.28π 【21教育名师】
5.(2016高考新课标II,理6)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为
A.20 B.24 C.28 D.32
6.(2015高考新课标I,理6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有21·cn·jy·com
A.14斛 B.22斛 C.36斛 D.66斛
7.(2015高考新课标I,理11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16 + 20,则r=
A.1 B.2 C.4 D.8
8.(2015高考新课标II,理6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为
A. B. C. D.
9.(2015高考新课标II,理9)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥体积的最大值为36,则球O的表面积为2·1·c·n·j·y
A.36π B.64π C.144π D.256π
1.某几何体的正视图与侧视图如图所示,则它的俯视图不可能是
A B C D www-2-1-cnjy-com
2.某几何体的三视图如图所示,则其体积为
A. B.2
C. D.
3.《九章算术》中将底面为长方形,且有一条侧棱与底面垂直的四棱锥称之为“阳马”.现有一阳马,其正视图和侧视图是如图所示的直角三角形.若该阳马的顶点都在同一个球面上,则该球的体积为【21教育】
A. B.
C. D.
4.已知三棱锥的外接球的球心恰好是线段的中点,且,则三棱锥的体积为
A. B.
C. D.
5.如图,在底面为矩形的四棱锥中,平面,,分别为棱,上一点,已知,,,且平面,四面体的每个顶点都在球的表面上,则球的表面积为
A. B.
C. D.
1.《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽丈,长丈;上棱长丈,无宽,高丈(如图).问它的体积是多少? ”这个问题的答案是21教育网
A. 立方丈 B. 立方丈
C. 立方丈 D. 立方丈
2.如图是一个空间几何体的三视图,其中正视图上半部分是一个底面边长为4、高为1的等腰三角形,正视图下半部分是一个边长为2的正方形,则该空间几何体的体积是21cnjy.com
A. B.
C. D.
3.点A,B,C,D均在同一球面上,且AB,AC,AD两两垂直,且, ,则该球的表面积为
A. B. C. D.
真题回顾:
1.B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成,如下图,则该几何体各面内只有两个相同的梯形,则这些梯形的面积之和为,故选B.【21·世纪·教育·网】
2.B【解析】由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积,上半部分是一个底面半径为3,高为6的圆柱的一半,其体积,故该组合体的体积.故选B.
3.B【解析】绘制圆柱的轴截面如图所示:由题意可得:,
结合勾股定理,底面半径,由圆柱的体积公式,可得圆柱的体积是,故选B.
4.A 【解析】由三视图知,该几何体的直观图如图所示:
是一个球被切掉左上角的,即该几何体是个球,设球的半径为,则,解得,所以它的表面积是的球面面积和三个扇形面积之和,即,故选A.
5.C【解析】由题意可知,圆柱的侧面积为,圆锥的侧面积为,圆柱的底面面积为,故该几何体的表面积为,故选C.
【名师点睛】由三视图还原几何体的方法:
6.B【解析】设圆锥底面半径为r,则 ,所以米堆的体积为 故堆放的米约为 故选B.
7.B【解析】由正视图和俯视图知,截圆柱的平面过圆柱的轴线,该几何体是半球与半个圆柱的组合体,圆柱的半径与球的半径都为r,圆柱的高为2r,其表面积为==16 + 20,解得r=2,故选B.21世纪教育网
8.D【解析】由三视图得,在正方体中,截去四面体,如图所示,设正方体棱长为,则,故剩余几何体的体积为,所以截去部分体积与剩余部分体积的比值为,故选D.21*教*育*名*师
9.C【解析】如图,当点C位于垂直于面的直径端点时,三棱锥的体积最大,设球的半径为,此时,故,则球的表面积为,故选C.
名校预测
1.【答案】C【解析】若几何体为两个圆锥体的组合体,则俯视图为A;若几何体为四棱锥与圆锥的组合体,则俯视图为B;若几何体为两个四棱锥的组合体,则俯视图为D;不可能为C,故选C.
2.【答案】C【解析】由三视图可知,该几何体为正八面体,即两个全等的正四棱锥,棱长为,高为,
所以其体积为,故选C.
3.【答案】C【解析】如图所示,该几何体为四棱锥.底面为矩形,其中底面,
.则该阳马的外接球的直径为∴该阳马的外接球的体积=故选C.
4.【答案】A【解析】因为三棱锥的外接球的球心恰好是线段的中点,所以为直角三角形,又,则为等腰直角三角形,21-cnjy*com
则,且,则平面,
所以.故选A.
5.【答案】C【解析】如图,在棱CD上取一点H,使得HD=1,平面BCE,
又平面BCE,平面平面BCE,又平面平面ABCD=GH,平面平面ABCD=BC,= HD=1,故四面体可以补成一个长方体,且长,宽,高分别为4,1,1,故球的表面积为 www.21-cn-jy.com
专家押题
1.【答案】A【解析】过点分别作平面和平面 垂直于底面,所以几何体的体积分为三部分中间是直三棱柱,两边是两个一样的四棱锥,所以立方丈,故选A.
2.【答案】B【解析】由三视图可知,几何体的上半部分为圆锥,下半部分为圆柱,故体积为.故选B.
3.【答案】B【解析】三棱锥的三条侧棱两两互相垂直,所以把它扩展为长方体,它也外接于球,对角线的长为球的直径,,它的外接球半径是,外接球的表面积是4π()2=14π.
同课章节目录
