向心加速度(山东省潍坊市安丘市)
文档属性
| 名称 | 向心加速度(山东省潍坊市安丘市) |  | |
| 格式 | rar | ||
| 文件大小 | 710.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2008-05-10 23:14:00 | ||
图片预览




文档简介
课件22张PPT。 我们已经知道,如果物体不受力,它将做匀速直线运动.
我们还知道,做曲线运动的物体速度一定是变化的.即使是我们上次课讨论的匀速圆周运动,其方向仍在不断变化着.
换句话说,做曲线运动的物体,一定有加速度.圆周运动是曲线运动,那么做圆周运动的物体,加速度的大小和方向如何确定呢?——这就是我们今天要研究的课题.
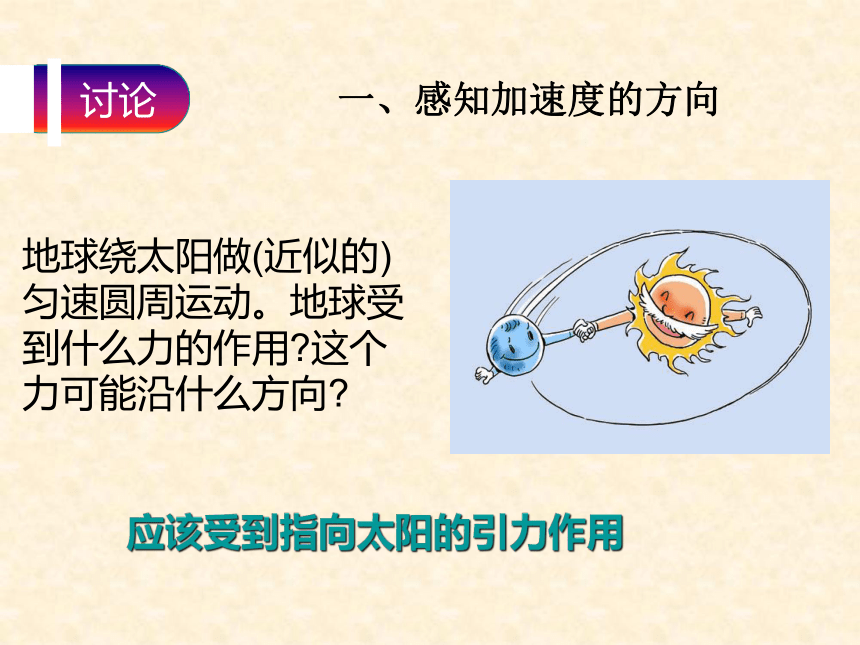
地球绕太阳做(近似的)匀速圆周运动。地球受到什么力的作用?这个
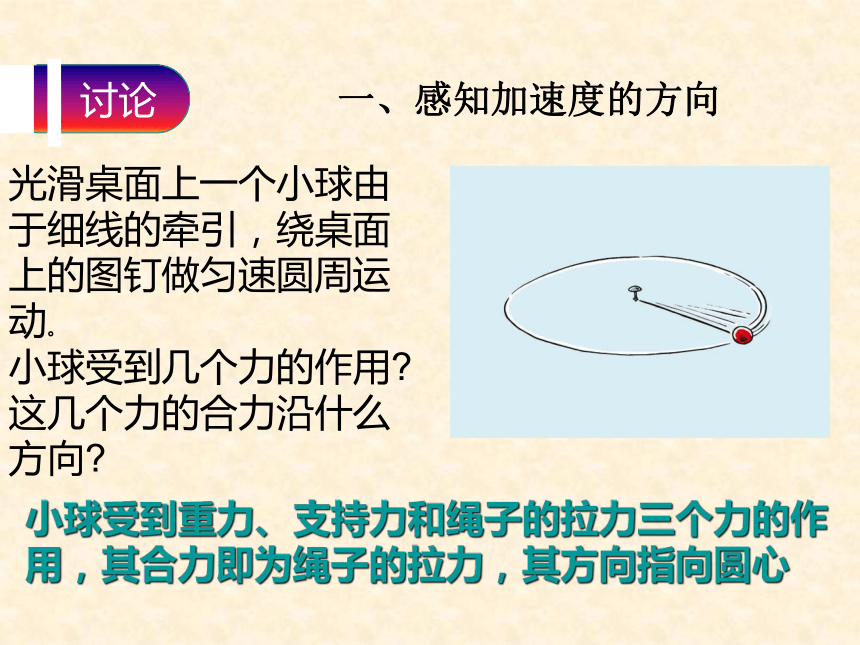
力可能沿什么方向? 一、感知加速度的方向 应该受到指向太阳的引力作用 光滑桌面上一个小球由于细线的牵引,绕桌面上的图钉做匀速圆周运动。
小球受到几个力的作用?
这几个力的合力沿什么方向? 小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心 一、感知加速度的方向 由于我们之前没有研究过曲线运动的加速度问题,特别是加速度的方向较难理解,而牛顿第二定律告诉我们,物体的加速度方向总是和它的受力方向一致,这个关系不仅对直线运动正确,对曲线运动也同样正确.所以先通过研究力来感知加速度,特别是加速度的方向.但我们具体研究时仍要根据加速度的定义来进行,为了进一步增加感性认识,请同学们再举出几个类似的做圆周运动的实例,并就刚才讨论的类似问题进行说明. 我们这节课要研究的是匀速圆周运动的加速度,可是以上两个例题却在研究物体所受的力,这不是“南辕北辙”了吗? 一、感知加速度的方向 在刚才的研究中,同学们已充分感知了做匀速圆周运动的物体所受的力或合外力指向圆心,所以物体的加速度也指向圆心.是不是由此可以得出结论:“任何物体做匀速圆周运动的加速度都指向圆心”?暂时不能,因为上面只研究了有限的实例.
还难以得出一般性的结论.然而,这样的研究十分有益,因为它强烈地向我们提示了问题的答案,给我们指出了方向.一、感知加速度的方向 二、速度变化量 重、难点:
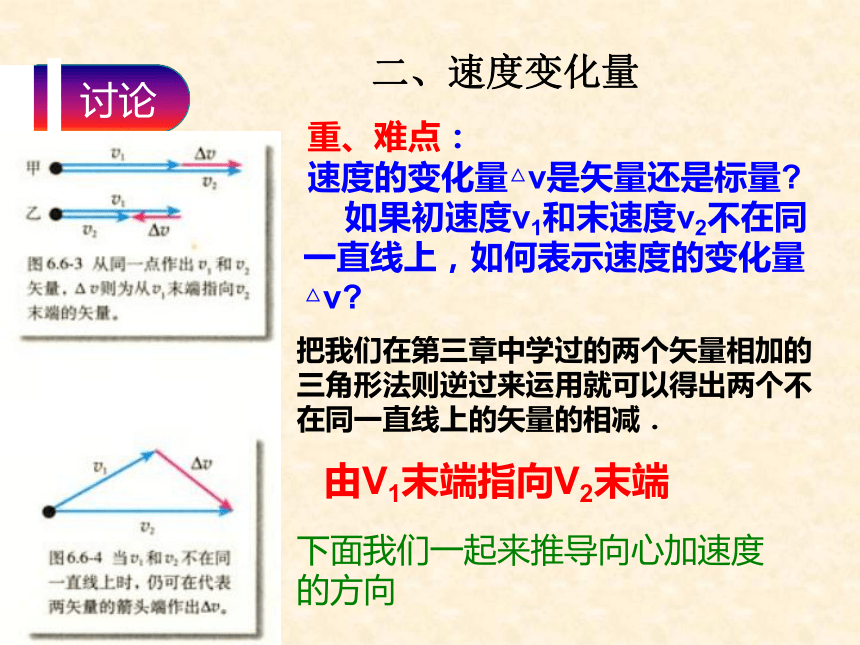
速度的变化量△v是矢量还是标量?
如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v?把我们在第三章中学过的两个矢量相加的三角形法则逆过来运用就可以得出两个不在同一直线上的矢量的相减.下面我们一起来推导向心加速度
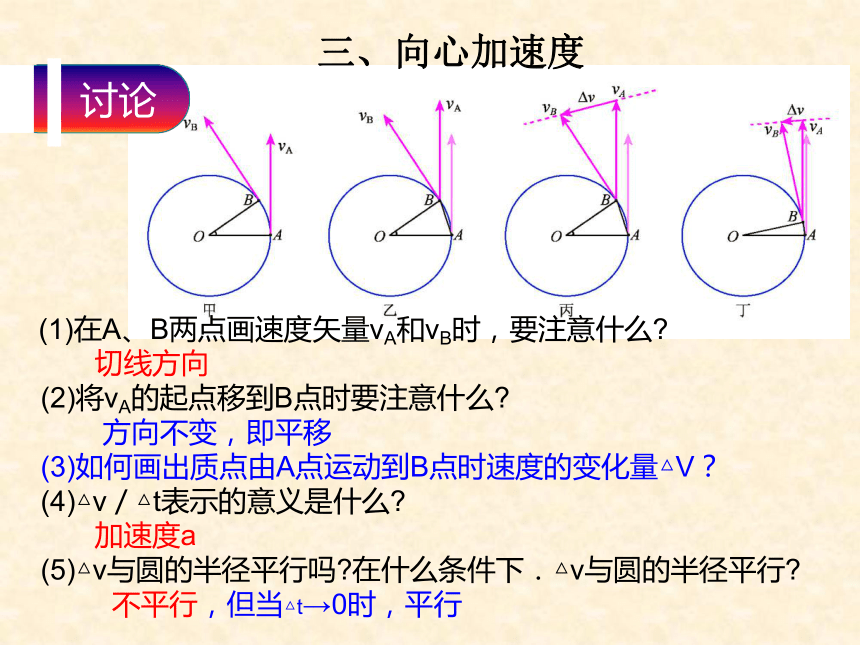
的方向由V1末端指向V2末端三、向心加速度 (1)在A、B两点画速度矢量vA和vB时,要注意什么?
切线方向
(2)将vA的起点移到B点时要注意什么?
方向不变,即平移
(3)如何画出质点由A点运动到B点时速度的变化量△V?
(4)△v/△t表示的意义是什么?
加速度a
(5)△v与圆的半径平行吗?在什么条件下.△v与圆的半径平行?
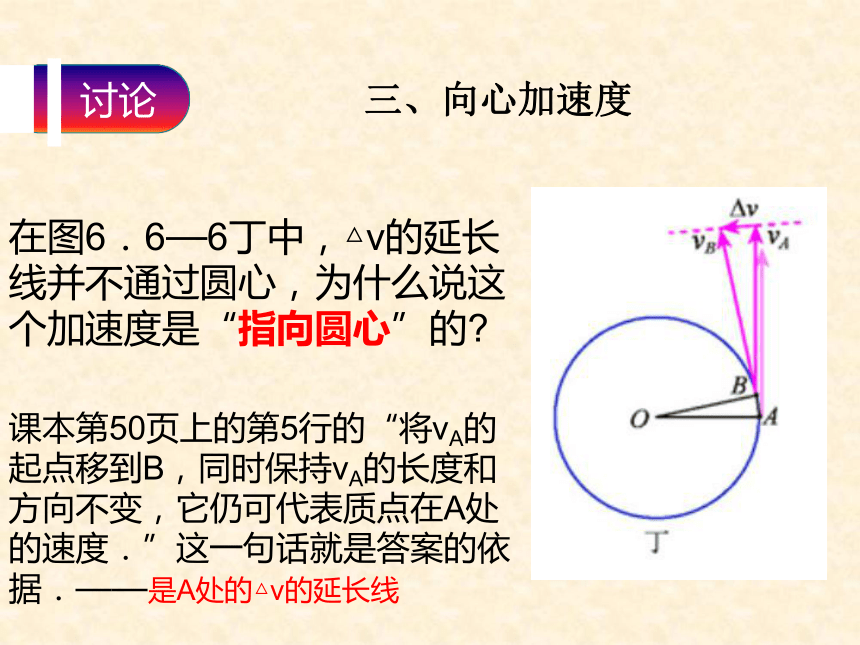
不平行,但当△t→0时,平行在图6.6—6丁中,△v的延长线并不通过圆心,为什么说这个加速度是“指向圆心”的?三、向心加速度课本第50页上的第5行的“将vA的起点移到B,同时保持vA的长度和方向不变,它仍可代表质点在A处的速度.”这一句话就是答案的依据.——是A处的△v的延长线上面的推导不涉及“地球公转”、“小球绕图钉转动”等具体的运动,结论具有一般性:做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.三、向心加速度的方向an=v2/r , an=rω2 三、向心加速度的大小按照课本第5l页“做一做”栏目中的提示,在练习本上推导出向心加速度的表达式 进一步的分析表明,由a= △v/△t可以导出向心加速度大小的表达式还有: an=vω 第5l页“做一做”栏目三、向心加速度表达式的推导过程正确认识向心加速度的两种表达式正确认识向心加速度的两种表达式 A、B两点的线速度V相同,适用于向心加速度与半径“成反比” B、C两点的角速度ω相同,适用于向心加速度与半径“成正比”下列关于向心加速度的说法中,正确的是 ( )
A.向心加速度的方向始终与速度的方向垂直 B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化A 如图6.6—10所示,长度为L=0.5m的轻杆,一端固定质量为M=1.0kg的小球A(小球的半径不计),另一端固定在一转动轴O上。小球绕轴在水平面上匀速转动的过程中,每隔0.1s杆转过的角度为30°。
试求:小球运动的向心加速度。 14 m/S2 一、感知做匀速圆周运动的物体加速度的方向
二、速度变化量的求法:
由V1末端指向V2末端
三、向心加速度:
(1)方向:总是指向圆心
(2)表达式:an=v2/r , an=rω2,
还有: an=vω
(3)对两种表达式的比较、分析 通过本节课的学习我们知道课堂练习
P52 1.2.3.4.
作业
P52 1.2.3
4待定
6.6 问题与练习参考解答:
1.答:
A.甲、乙线速度相等时,利用an=v2/r,半径小的向心加速度
大。所以乙的向心加速度大;
B. 甲、乙周期相等时,利用 an=4π2r/T2,半径小的向心加速
度大。所以乙的向心加速度大;
C. 甲、乙角速度相等时,利用an=vω,线速度大的向心加速度
大。所以乙的向心加速度小;
D. 甲、乙线速度相等时,利用an= vω,角速度大的向心加速
度大。由于在相等时间内甲与圆心的连线扫过的角度比乙
大,所以甲的角速度大,甲的向心加速度大。2.解:月球公转周期 T=27.3×24×3600s=2.36×106s
月球公转的向心加速度为 an=4π2r/T2=2.7×10-3m/s23.解:
A、B两个快艇做匀速圆周运动,由于在相等时间内,它们通过的路程之比是4:3,所以它们的线速度之比为4:3;由于在相等时间内,它们运动方向改变的角度之比是3:2,所以它们的角速度之比为3:2。由于向心加速度 an= vω,所以它们的向心加速度之比为2:1。
4.解:
(1)由于皮带与两轮之间不发生滑动,所以两轮边缘上各点的线速度大小相等,设电动机皮带轮与机器皮带轮边缘上质点的线速度大小分别为V1、V2,角速度大小分别为ω1、ω2,边缘上质点运动的半径分别为r1、r2,则
V1=V2 V1=ω1r1 V2=ω2r2 又ω=2πn
所以 n1:n2=ω1:ω2=r2:r1=3:1
(2)A点的向心加速度为 anA=ω22r2/2=0.05m/s2
(3)电动机皮带轮边缘上质点的向心加速度为 an=V12/r1=0.30m/s2
我们还知道,做曲线运动的物体速度一定是变化的.即使是我们上次课讨论的匀速圆周运动,其方向仍在不断变化着.
换句话说,做曲线运动的物体,一定有加速度.圆周运动是曲线运动,那么做圆周运动的物体,加速度的大小和方向如何确定呢?——这就是我们今天要研究的课题.
地球绕太阳做(近似的)匀速圆周运动。地球受到什么力的作用?这个
力可能沿什么方向? 一、感知加速度的方向 应该受到指向太阳的引力作用 光滑桌面上一个小球由于细线的牵引,绕桌面上的图钉做匀速圆周运动。
小球受到几个力的作用?
这几个力的合力沿什么方向? 小球受到重力、支持力和绳子的拉力三个力的作用,其合力即为绳子的拉力,其方向指向圆心 一、感知加速度的方向 由于我们之前没有研究过曲线运动的加速度问题,特别是加速度的方向较难理解,而牛顿第二定律告诉我们,物体的加速度方向总是和它的受力方向一致,这个关系不仅对直线运动正确,对曲线运动也同样正确.所以先通过研究力来感知加速度,特别是加速度的方向.但我们具体研究时仍要根据加速度的定义来进行,为了进一步增加感性认识,请同学们再举出几个类似的做圆周运动的实例,并就刚才讨论的类似问题进行说明. 我们这节课要研究的是匀速圆周运动的加速度,可是以上两个例题却在研究物体所受的力,这不是“南辕北辙”了吗? 一、感知加速度的方向 在刚才的研究中,同学们已充分感知了做匀速圆周运动的物体所受的力或合外力指向圆心,所以物体的加速度也指向圆心.是不是由此可以得出结论:“任何物体做匀速圆周运动的加速度都指向圆心”?暂时不能,因为上面只研究了有限的实例.
还难以得出一般性的结论.然而,这样的研究十分有益,因为它强烈地向我们提示了问题的答案,给我们指出了方向.一、感知加速度的方向 二、速度变化量 重、难点:
速度的变化量△v是矢量还是标量?
如果初速度v1和末速度v2不在同一直线上,如何表示速度的变化量△v?把我们在第三章中学过的两个矢量相加的三角形法则逆过来运用就可以得出两个不在同一直线上的矢量的相减.下面我们一起来推导向心加速度
的方向由V1末端指向V2末端三、向心加速度 (1)在A、B两点画速度矢量vA和vB时,要注意什么?
切线方向
(2)将vA的起点移到B点时要注意什么?
方向不变,即平移
(3)如何画出质点由A点运动到B点时速度的变化量△V?
(4)△v/△t表示的意义是什么?
加速度a
(5)△v与圆的半径平行吗?在什么条件下.△v与圆的半径平行?
不平行,但当△t→0时,平行在图6.6—6丁中,△v的延长线并不通过圆心,为什么说这个加速度是“指向圆心”的?三、向心加速度课本第50页上的第5行的“将vA的起点移到B,同时保持vA的长度和方向不变,它仍可代表质点在A处的速度.”这一句话就是答案的依据.——是A处的△v的延长线上面的推导不涉及“地球公转”、“小球绕图钉转动”等具体的运动,结论具有一般性:做匀速圆周运动的物体加速度指向圆心.这个加速度称为向心加速度.三、向心加速度的方向an=v2/r , an=rω2 三、向心加速度的大小按照课本第5l页“做一做”栏目中的提示,在练习本上推导出向心加速度的表达式 进一步的分析表明,由a= △v/△t可以导出向心加速度大小的表达式还有: an=vω 第5l页“做一做”栏目三、向心加速度表达式的推导过程正确认识向心加速度的两种表达式正确认识向心加速度的两种表达式 A、B两点的线速度V相同,适用于向心加速度与半径“成反比” B、C两点的角速度ω相同,适用于向心加速度与半径“成正比”下列关于向心加速度的说法中,正确的是 ( )
A.向心加速度的方向始终与速度的方向垂直 B.向心加速度的方向保持不变
C.在匀速圆周运动中,向心加速度是恒定的
D.在匀速圆周运动中,向心加速度的大小不断变化A 如图6.6—10所示,长度为L=0.5m的轻杆,一端固定质量为M=1.0kg的小球A(小球的半径不计),另一端固定在一转动轴O上。小球绕轴在水平面上匀速转动的过程中,每隔0.1s杆转过的角度为30°。
试求:小球运动的向心加速度。 14 m/S2 一、感知做匀速圆周运动的物体加速度的方向
二、速度变化量的求法:
由V1末端指向V2末端
三、向心加速度:
(1)方向:总是指向圆心
(2)表达式:an=v2/r , an=rω2,
还有: an=vω
(3)对两种表达式的比较、分析 通过本节课的学习我们知道课堂练习
P52 1.2.3.4.
作业
P52 1.2.3
4待定
6.6 问题与练习参考解答:
1.答:
A.甲、乙线速度相等时,利用an=v2/r,半径小的向心加速度
大。所以乙的向心加速度大;
B. 甲、乙周期相等时,利用 an=4π2r/T2,半径小的向心加速
度大。所以乙的向心加速度大;
C. 甲、乙角速度相等时,利用an=vω,线速度大的向心加速度
大。所以乙的向心加速度小;
D. 甲、乙线速度相等时,利用an= vω,角速度大的向心加速
度大。由于在相等时间内甲与圆心的连线扫过的角度比乙
大,所以甲的角速度大,甲的向心加速度大。2.解:月球公转周期 T=27.3×24×3600s=2.36×106s
月球公转的向心加速度为 an=4π2r/T2=2.7×10-3m/s23.解:
A、B两个快艇做匀速圆周运动,由于在相等时间内,它们通过的路程之比是4:3,所以它们的线速度之比为4:3;由于在相等时间内,它们运动方向改变的角度之比是3:2,所以它们的角速度之比为3:2。由于向心加速度 an= vω,所以它们的向心加速度之比为2:1。
4.解:
(1)由于皮带与两轮之间不发生滑动,所以两轮边缘上各点的线速度大小相等,设电动机皮带轮与机器皮带轮边缘上质点的线速度大小分别为V1、V2,角速度大小分别为ω1、ω2,边缘上质点运动的半径分别为r1、r2,则
V1=V2 V1=ω1r1 V2=ω2r2 又ω=2πn
所以 n1:n2=ω1:ω2=r2:r1=3:1
(2)A点的向心加速度为 anA=ω22r2/2=0.05m/s2
(3)电动机皮带轮边缘上质点的向心加速度为 an=V12/r1=0.30m/s2
