人教版2018年中考数学复习24数学说题课件 (共21张PPT)
文档属性
| 名称 | 人教版2018年中考数学复习24数学说题课件 (共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 10.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-27 00:00:00 | ||
图片预览






文档简介
(共21张PPT)
中考 24数学说题
解题
方法
解题
思路
说 题
说题流程
变式
推广
阐述
题意
课后
反思
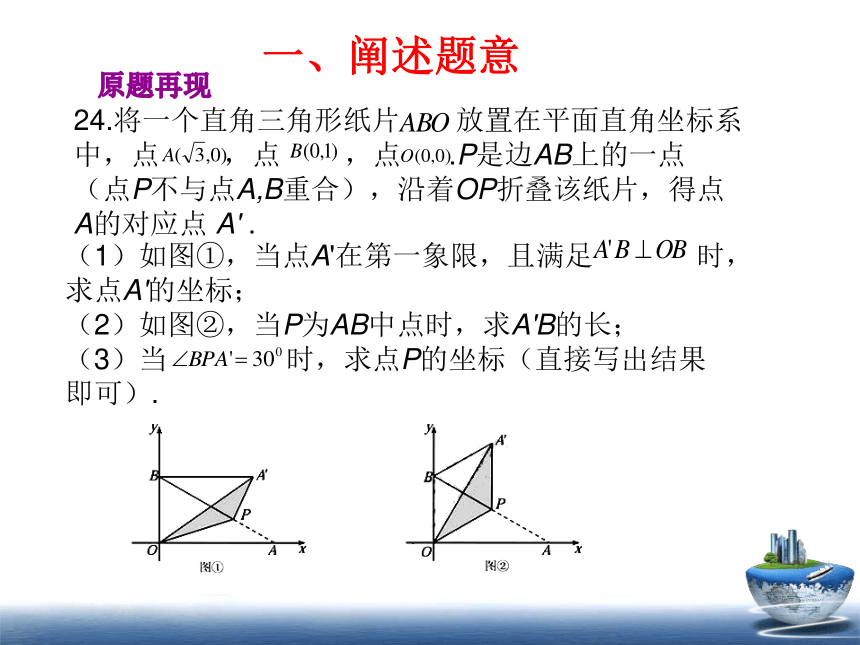
24.将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点 .P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点 A' .
原题再现
(1)如图①,当点A'在第一象限,且满足 时, 求点A'的坐标;
(2)如图②,当P为AB中点时,求A'B的长;
(3)当 时,求点P的坐标(直接写出结果即可).
一、阐述题意
设计意图
本题以能力立意,考察学生综合运用
轴对称变换,动点问题的基础知识与基本方法解决问题的能力。
知识考查
主要考查了平面直角坐标系,勾股定理
全等三角形,体现在第一问。
直角三角形,等腰(边)三角形,
平行四边形,特殊的平行四边形以及解直角三角形体现在第二问。
等知识的综合应用。
侧重考察学生分析问题,转化问题,解决问题能力和计算的能力。
数学思想
方程思想
数形结合思想
分类思想
转化思想
知识背景
本题是图形变换中的轴对称变换一类试题。
将几何图形置于平面直角坐标系中,使"数"与"形"有机地结合在一起,很好地体现了数形结合的数学思想;而通过对几何图形运动变化,使学生经历由观察、想象、推理等发现、探索的过程,是中考数学试题中,充分体现考查同学们综合素质教育和思想的题目。
二、思路与解题
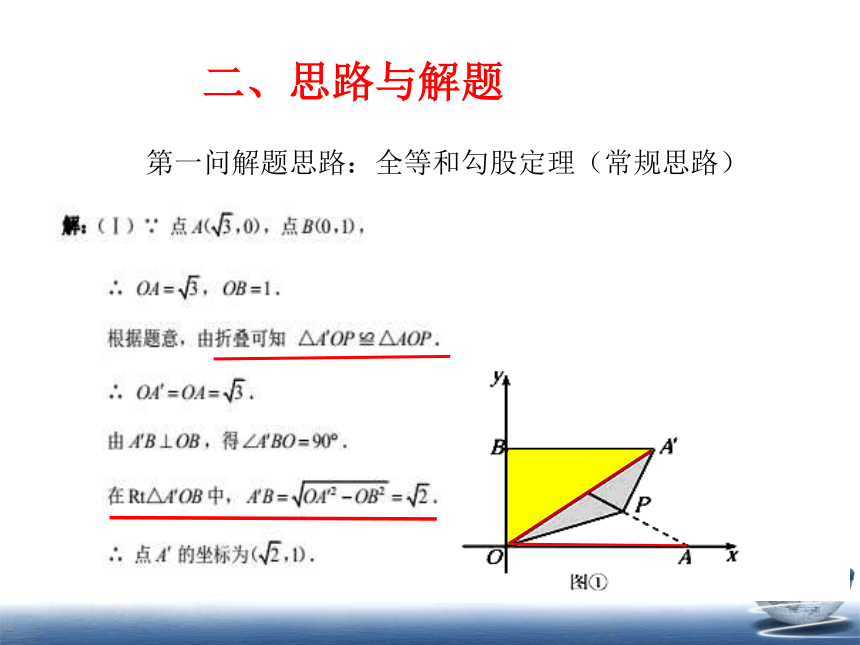
第一问解题思路:全等和勾股定理(常规思路)
第二问的思路与解法:
本题是求线段,基本思路证全等,证平行四边形,利用中垂线等方法
1. 利用直角三角形斜边中点 全等等知识证明平行四边形(标准答案)
2.利用特殊直角三角形解(证明菱形或证全等或者中垂线知识等)
3.做辅助线延长A'P(一条或两条)
观察图形,拆分图形
几何直观
猜想---推理---证明
解法一:利用平行四边形的性质
平行四边形的判定和性质
边
角
对角线
解法二:利用特殊直角三角形
中点性质
由题意得 300
600
AP=OP=BP=OB=A'P,
OA'=OA
M为BP,OA'中点,且BP OA'
OB=A'B
M
中垂线
M
解法三:构造直角三角形
过点P,A'分别做PM┴x
轴于点M,A'N┴y轴于点N
由前知 600
OM=
BN=
根据勾股定理求A'B=1
N
根据直角
构造直角三角形或者矩形
(3)当 时,求点P的坐标(直接写出结果即可).
答案:
A'
A'
变式1 :是否存在一点P,使四边形OBA'P为菱形,若存在请求出P点坐标。若不存在说明理由?
变式2:是否存在一点P,使三角形OBA'为
等腰三角形,若存在请求出P点坐标。
若不存在说明理由?
变式3:三角形OPA旋转600时,点P的坐标?
(2)如图②,当P为AB中点时,求A'B的长;
三、变式推广
四、课后反思
学生得分情况
本题考察的知识点比较多,综合性强,源于教材但又高于教材,对学生的能力和应用能力有较高的要求,所以得分率不乐观
学生难点
1.对求坐标的一般方法思路不清
2.求线段长的一般思路不清晰
3.构造直角三角形的方法掌握不好。
4.挖掘隐含条件是对学生很高的要求。
5.动点问题中数形结合的思想学生掌握难度很大。
学生易错点
1.相关的定义,性质不清晰。
2.忽略了利用特殊直角三角形证题、解题。
3.计算能力不足。
4.分析问题能力不足。
教学反思
1.从知识上,教师要立足于落实双基,使学生全面掌握知识方法。
比如:课本例题,课后练习,复习巩固等落实
2.从方法上,注重学生知识的迁移能力。
比如:证明题的逆向思维,证明线段相等的常规思路。
3.从效果上,达到“一题多解、一题多变、多题同解、错例众评”的教学效果。
五、总结提炼
本题是将几何图形放到直角坐标系中通过翻折研究图形中的点,线问题。
解这类问题的关键要抓住图形的变换的实质。注意挖掘隐含条件,用数形结合的思想,分类讨论的思想解决问题。
结束语
通过研究这道中考题使我深刻体会,在我们数学教学的过程中 应该怎么做?
1.不能盲目的追求数量不顾质量,采用题海战术。
2.思考,善于思考,进行一题多解法的训练和变式训练
通过对一道题目多思路解法,多变式训练,既能促使学生沟通知识点间的联系,又培养了学生的思维能力 。
3. 引导学生多方法,多视角思考问题和发现问题,形成良好的思维品质,而且使自己感受到成功的喜悦和增强自信心,也极大地激发学生学习数学的积极性和浓厚的兴趣,从而在很大程度上培养了学生思维的广阔性。使学生从中学到“转化策略、数形结合、函数与方程”等基本的数学思想。
学生的思维迁移、发散、开拓和活跃,提高学生思维的敏捷性和灵活性,从而提高分析与解答数学题的能力。
4.注重小结,养成学生通过对比、小结,得出自己的体会,充分发掘自身的潜能,从而提高自己的解题能力。
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么!
——毕达哥拉斯
谢谢,请多提宝贵意见!
中考 24数学说题
解题
方法
解题
思路
说 题
说题流程
变式
推广
阐述
题意
课后
反思
24.将一个直角三角形纸片 放置在平面直角坐标系中,点 ,点 ,点 .P是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点 A' .
原题再现
(1)如图①,当点A'在第一象限,且满足 时, 求点A'的坐标;
(2)如图②,当P为AB中点时,求A'B的长;
(3)当 时,求点P的坐标(直接写出结果即可).
一、阐述题意
设计意图
本题以能力立意,考察学生综合运用
轴对称变换,动点问题的基础知识与基本方法解决问题的能力。
知识考查
主要考查了平面直角坐标系,勾股定理
全等三角形,体现在第一问。
直角三角形,等腰(边)三角形,
平行四边形,特殊的平行四边形以及解直角三角形体现在第二问。
等知识的综合应用。
侧重考察学生分析问题,转化问题,解决问题能力和计算的能力。
数学思想
方程思想
数形结合思想
分类思想
转化思想
知识背景
本题是图形变换中的轴对称变换一类试题。
将几何图形置于平面直角坐标系中,使"数"与"形"有机地结合在一起,很好地体现了数形结合的数学思想;而通过对几何图形运动变化,使学生经历由观察、想象、推理等发现、探索的过程,是中考数学试题中,充分体现考查同学们综合素质教育和思想的题目。
二、思路与解题
第一问解题思路:全等和勾股定理(常规思路)
第二问的思路与解法:
本题是求线段,基本思路证全等,证平行四边形,利用中垂线等方法
1. 利用直角三角形斜边中点 全等等知识证明平行四边形(标准答案)
2.利用特殊直角三角形解(证明菱形或证全等或者中垂线知识等)
3.做辅助线延长A'P(一条或两条)
观察图形,拆分图形
几何直观
猜想---推理---证明
解法一:利用平行四边形的性质
平行四边形的判定和性质
边
角
对角线
解法二:利用特殊直角三角形
中点性质
由题意得 300
600
AP=OP=BP=OB=A'P,
OA'=OA
M为BP,OA'中点,且BP OA'
OB=A'B
M
中垂线
M
解法三:构造直角三角形
过点P,A'分别做PM┴x
轴于点M,A'N┴y轴于点N
由前知 600
OM=
BN=
根据勾股定理求A'B=1
N
根据直角
构造直角三角形或者矩形
(3)当 时,求点P的坐标(直接写出结果即可).
答案:
A'
A'
变式1 :是否存在一点P,使四边形OBA'P为菱形,若存在请求出P点坐标。若不存在说明理由?
变式2:是否存在一点P,使三角形OBA'为
等腰三角形,若存在请求出P点坐标。
若不存在说明理由?
变式3:三角形OPA旋转600时,点P的坐标?
(2)如图②,当P为AB中点时,求A'B的长;
三、变式推广
四、课后反思
学生得分情况
本题考察的知识点比较多,综合性强,源于教材但又高于教材,对学生的能力和应用能力有较高的要求,所以得分率不乐观
学生难点
1.对求坐标的一般方法思路不清
2.求线段长的一般思路不清晰
3.构造直角三角形的方法掌握不好。
4.挖掘隐含条件是对学生很高的要求。
5.动点问题中数形结合的思想学生掌握难度很大。
学生易错点
1.相关的定义,性质不清晰。
2.忽略了利用特殊直角三角形证题、解题。
3.计算能力不足。
4.分析问题能力不足。
教学反思
1.从知识上,教师要立足于落实双基,使学生全面掌握知识方法。
比如:课本例题,课后练习,复习巩固等落实
2.从方法上,注重学生知识的迁移能力。
比如:证明题的逆向思维,证明线段相等的常规思路。
3.从效果上,达到“一题多解、一题多变、多题同解、错例众评”的教学效果。
五、总结提炼
本题是将几何图形放到直角坐标系中通过翻折研究图形中的点,线问题。
解这类问题的关键要抓住图形的变换的实质。注意挖掘隐含条件,用数形结合的思想,分类讨论的思想解决问题。
结束语
通过研究这道中考题使我深刻体会,在我们数学教学的过程中 应该怎么做?
1.不能盲目的追求数量不顾质量,采用题海战术。
2.思考,善于思考,进行一题多解法的训练和变式训练
通过对一道题目多思路解法,多变式训练,既能促使学生沟通知识点间的联系,又培养了学生的思维能力 。
3. 引导学生多方法,多视角思考问题和发现问题,形成良好的思维品质,而且使自己感受到成功的喜悦和增强自信心,也极大地激发学生学习数学的积极性和浓厚的兴趣,从而在很大程度上培养了学生思维的广阔性。使学生从中学到“转化策略、数形结合、函数与方程”等基本的数学思想。
学生的思维迁移、发散、开拓和活跃,提高学生思维的敏捷性和灵活性,从而提高分析与解答数学题的能力。
4.注重小结,养成学生通过对比、小结,得出自己的体会,充分发掘自身的潜能,从而提高自己的解题能力。
在数学的天地里,重要的不是我们知道什么,而是我们怎么知道什么!
——毕达哥拉斯
谢谢,请多提宝贵意见!
同课章节目录
