26.1.2 反比例函数的图象和性质课件(第一课时)
文档属性
| 名称 | 26.1.2 反比例函数的图象和性质课件(第一课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-27 00:00:00 | ||
图片预览



文档简介
课件24张PPT。讲课内容:课本4-6页
§26.1.2 反比例函数的图象和性质(第1课时)数学九年级下
一、新课引入 1、过点(2,5)的反比例函数的解析式是: .
2、一次函数y=2x-1的图象是 ,y随x的增大而 .
3、用描点法作函数图象的步骤:
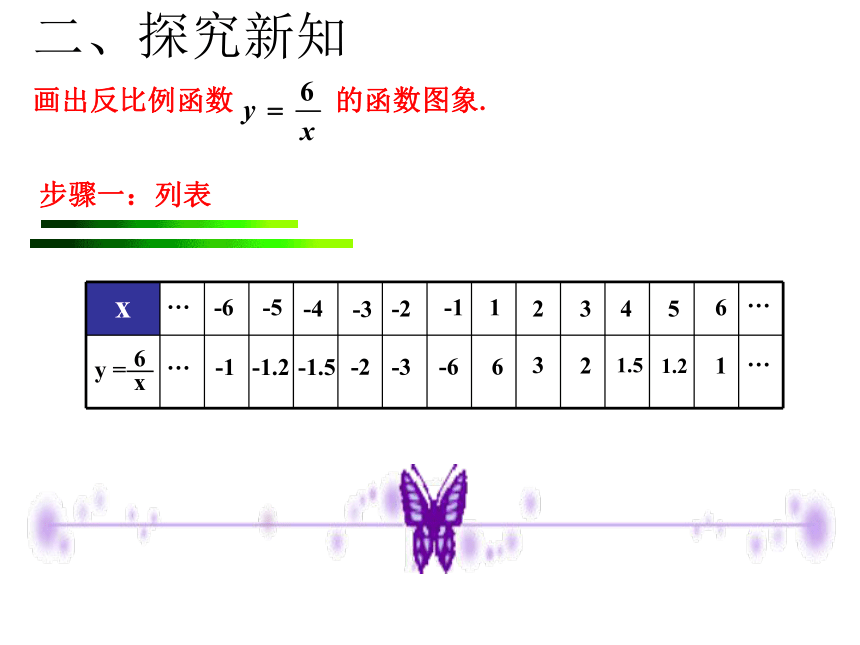
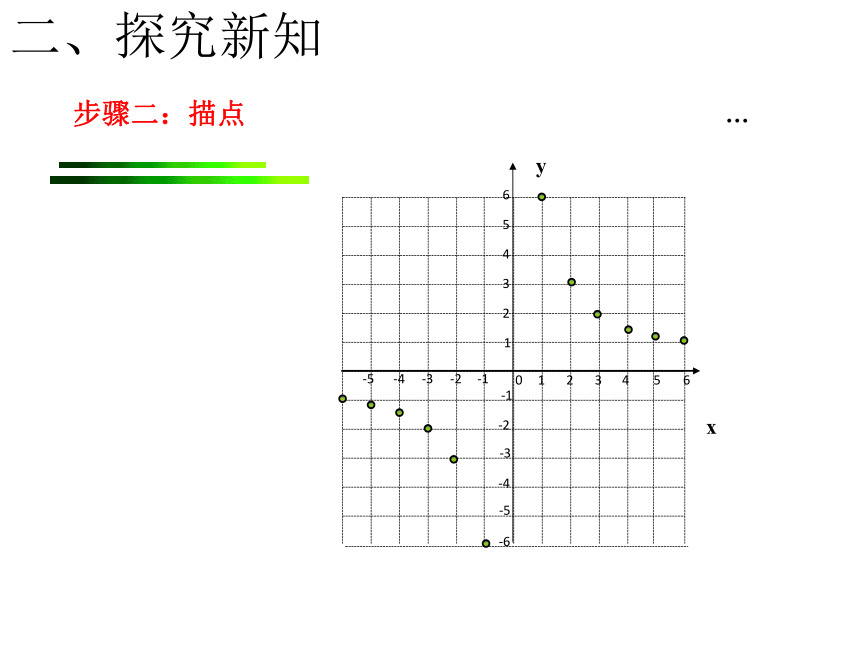
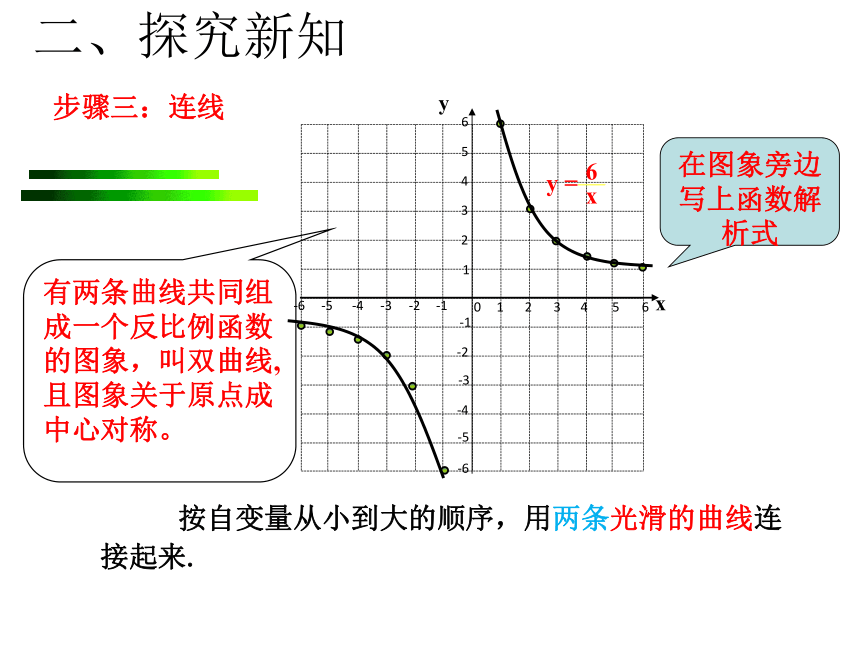
_______________________________________ 一条直线增大列表,描点,连线学习目标 1 .会用描点法画反比例函数的图象 .2.结合图象分析并掌握反比例函数的性质 3.体会函数的三种表示方法,领会数形结合的思想方法.步骤一:列表画出反比例函数 的函数图象.16233241.551.261-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………二、探究新知 步骤二:描点123456-1-3-2-4-51234-1-2-3-40-6-556x…y二、探究新知 步骤三:连线 按自变量从小到大的顺序,用两条光滑的曲线连接起来.123456-1-3-2-4-5-61234-1-2-3-40-6-556x有两条曲线共同组
成一个反比例函数
的图象,叫双曲线, 且图象关于原点成
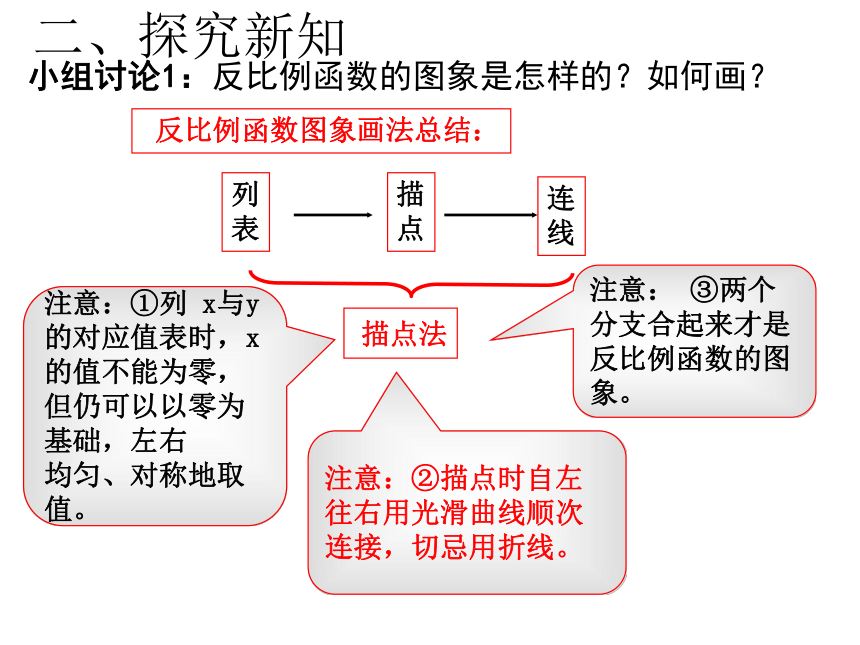
中心对称。y在图象旁边写上函数解析式二、探究新知 注意:①列 x与y的对应值表时,x的值不能为零,但仍可以以零为基础,左右
均匀、对称地取值。注意:②描点时自左往右用光滑曲线顺次连接,切忌用折线。注意: ③两个分支合起来才是反比例函数的图象。小组讨论1:反比例函数的图象是怎样的?如何画?二、探究新知 【课时小结】在平面直角坐标系中画出反比例函数y= 的
图象.观察图象,分析:
(1)它们有什么共同特征和不同点?
(2)图象分别位于哪几个象限? 解:画图略.
(1)由两条曲线组成,并且随着x的不断增大(或减小),曲线越来越接近x轴(或y轴).
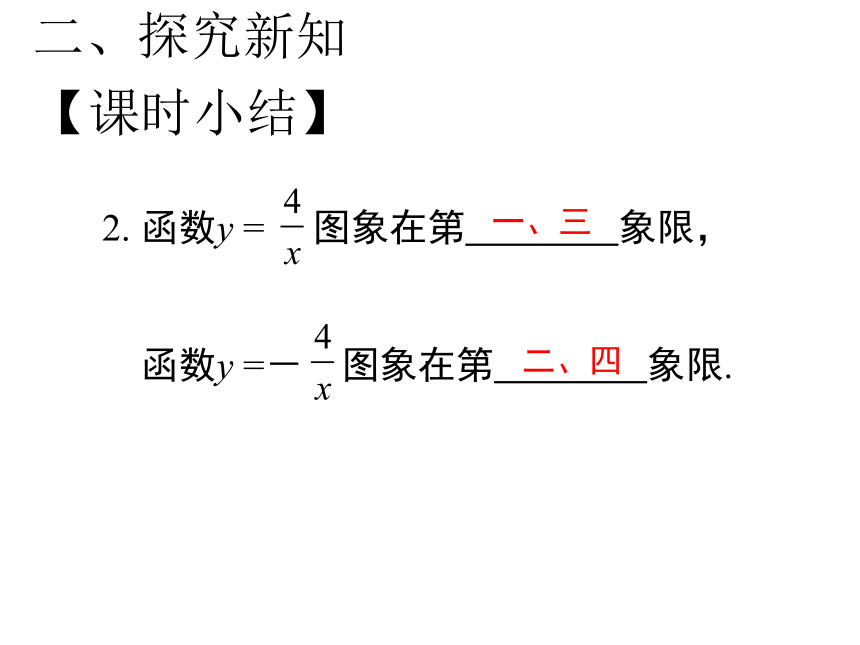
(2)它的图象分别位于第一、三两个象限, 二、探究新知 2. 函数y = 图象在第____象限,
函数y =- 图象在第____象限. 一、三二、四二、探究新知 【课时小结】1、在平面直角坐标系中画出反比例
函数y= 和y= - 的图象.(1)每个函数的图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数y=k/x(k>0),考虑问题(1)(2),你能得出同样的结论吗?二、探究新知 一般地,反比例函数y=k/x的图像是双曲线,它具有以下性质:
(1)当k>0时,双曲线的两支分别位于第一、三象限,在每一个象限内,y随x的增大而减小;
(2)当k<0时,双曲线的两支分别位于第二、四象限,在每一个象限内,y随x的增大而增大.三、归纳小结1、反比例函数y= (k为常数,k≠0)的图象是 ( )
2、当k>0时,双曲线的两支分别位于第__________象限,在每个象限内,y值随x值的增大而____________
3、当k<0时,双曲线的两支分别位于第__________象限,在每个象限内,y值随x值的增大_____.一、三减小二、四增大三、归纳小结双曲线四、强化训练 1、如图,这是下列四个函数中哪一个函数的图象?( )
y = 5x
(B) y = 2x+3
y =
(D) y = - C2、请指出下面的图象
中哪一个是反比例函
数的图象( )D四、强化训练 3、如果点(1,-2)在某双曲线上,那么该双
曲线的解析式为 .
4、下列函数中,当x>0时,y随x的增大而减小的是( ).
(A) y=x (B)
(C) (D) y=2xB四、强化训练 5、下列反比例函数图象一定在第一、三象限的是( ).
(B)
(D)
6、已知反比例函数y= 的图象在第一、三象限内,则k的值可是________(写出满足条件的一个k值即可).C3四、强化训练 6.下列图象分别是什么函数的图象四、强化训练 7.如图所示的图象对应的函数解析式为( )四、强化训练 反比例函数y= (k为常数,k≠0)的图象是双曲线,它具有以下性质:五、课堂小结回顾本节课的学习历程,你有哪些收获? (1)当k>0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小; (2)当k<0时,双曲线的两支分别位于第二、第四
象限,在每一个象限内,y随x的增大而增大. 四、课堂作业
课本108页:3、5题。谢谢拓展提高 1.指出当k>0时,下列图象中哪些可能是y=kx
与y= (k≠0)在同一坐标系中的图象
( )B拓展提高2.抛物线y=ax2+bx+c图像如图所示,则一次函数
y= -bx-4ac+ b2与反比例函数 在同一
坐标系内的图像大致为( ) D拓展提高 3. 已知正比例函数y=﹣4x与反比例函数y=
的图象交于A、B两点,若点A的坐标为(x,
4),则点B的坐标为________. (1,-4) 4. 在平面直角坐标系内,过反比例函数y=
(k>0)的图象上的一点分别作x轴、y轴的垂
线段,与x轴、y轴所围成的矩形面积是6,则
函数解析式为 .
一、新课引入 1、过点(2,5)的反比例函数的解析式是: .
2、一次函数y=2x-1的图象是 ,y随x的增大而 .
3、用描点法作函数图象的步骤:
_______________________________________ 一条直线增大列表,描点,连线学习目标 1 .会用描点法画反比例函数的图象 .2.结合图象分析并掌握反比例函数的性质 3.体会函数的三种表示方法,领会数形结合的思想方法.步骤一:列表画出反比例函数 的函数图象.16233241.551.261-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………二、探究新知 步骤二:描点123456-1-3-2-4-51234-1-2-3-40-6-556x…y二、探究新知 步骤三:连线 按自变量从小到大的顺序,用两条光滑的曲线连接起来.123456-1-3-2-4-5-61234-1-2-3-40-6-556x有两条曲线共同组
成一个反比例函数
的图象,叫双曲线, 且图象关于原点成
中心对称。y在图象旁边写上函数解析式二、探究新知 注意:①列 x与y的对应值表时,x的值不能为零,但仍可以以零为基础,左右
均匀、对称地取值。注意:②描点时自左往右用光滑曲线顺次连接,切忌用折线。注意: ③两个分支合起来才是反比例函数的图象。小组讨论1:反比例函数的图象是怎样的?如何画?二、探究新知 【课时小结】在平面直角坐标系中画出反比例函数y= 的
图象.观察图象,分析:
(1)它们有什么共同特征和不同点?
(2)图象分别位于哪几个象限? 解:画图略.
(1)由两条曲线组成,并且随着x的不断增大(或减小),曲线越来越接近x轴(或y轴).
(2)它的图象分别位于第一、三两个象限, 二、探究新知 2. 函数y = 图象在第____象限,
函数y =- 图象在第____象限. 一、三二、四二、探究新知 【课时小结】1、在平面直角坐标系中画出反比例
函数y= 和y= - 的图象.(1)每个函数的图象分别位于哪些象限?
(2)在每一个象限内,随着x的增大,y如何变化?你能由它们的解析式说明理由吗?
(3)对于反比例函数y=k/x(k>0),考虑问题(1)(2),你能得出同样的结论吗?二、探究新知 一般地,反比例函数y=k/x的图像是双曲线,它具有以下性质:
(1)当k>0时,双曲线的两支分别位于第一、三象限,在每一个象限内,y随x的增大而减小;
(2)当k<0时,双曲线的两支分别位于第二、四象限,在每一个象限内,y随x的增大而增大.三、归纳小结1、反比例函数y= (k为常数,k≠0)的图象是 ( )
2、当k>0时,双曲线的两支分别位于第__________象限,在每个象限内,y值随x值的增大而____________
3、当k<0时,双曲线的两支分别位于第__________象限,在每个象限内,y值随x值的增大_____.一、三减小二、四增大三、归纳小结双曲线四、强化训练 1、如图,这是下列四个函数中哪一个函数的图象?( )
y = 5x
(B) y = 2x+3
y =
(D) y = - C2、请指出下面的图象
中哪一个是反比例函
数的图象( )D四、强化训练 3、如果点(1,-2)在某双曲线上,那么该双
曲线的解析式为 .
4、下列函数中,当x>0时,y随x的增大而减小的是( ).
(A) y=x (B)
(C) (D) y=2xB四、强化训练 5、下列反比例函数图象一定在第一、三象限的是( ).
(B)
(D)
6、已知反比例函数y= 的图象在第一、三象限内,则k的值可是________(写出满足条件的一个k值即可).C3四、强化训练 6.下列图象分别是什么函数的图象四、强化训练 7.如图所示的图象对应的函数解析式为( )四、强化训练 反比例函数y= (k为常数,k≠0)的图象是双曲线,它具有以下性质:五、课堂小结回顾本节课的学习历程,你有哪些收获? (1)当k>0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小; (2)当k<0时,双曲线的两支分别位于第二、第四
象限,在每一个象限内,y随x的增大而增大. 四、课堂作业
课本108页:3、5题。谢谢拓展提高 1.指出当k>0时,下列图象中哪些可能是y=kx
与y= (k≠0)在同一坐标系中的图象
( )B拓展提高2.抛物线y=ax2+bx+c图像如图所示,则一次函数
y= -bx-4ac+ b2与反比例函数 在同一
坐标系内的图像大致为( ) D拓展提高 3. 已知正比例函数y=﹣4x与反比例函数y=
的图象交于A、B两点,若点A的坐标为(x,
4),则点B的坐标为________. (1,-4) 4. 在平面直角坐标系内,过反比例函数y=
(k>0)的图象上的一点分别作x轴、y轴的垂
线段,与x轴、y轴所围成的矩形面积是6,则
函数解析式为 .
