人教版九年级下册数学同步练习:27.2.2相似三角形的性质(附答案)
文档属性
| 名称 | 人教版九年级下册数学同步练习:27.2.2相似三角形的性质(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 441.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-29 00:00:00 | ||
图片预览


文档简介
《27.2.2相似三角形的性质》分层练习
一.基础题
1.已知△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,且=,B′D′=4,则BD的长为 。21世纪教育网版权所有
2.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,且AD=8 cm, A′D′=3 cm.,则△ABC与△A′B′C′对应高的比为 。
3.两个相似三角形的相似比为2∶3,它们周长的差是25,那么较大三角形的周长是________,这两个三角形的面积比为 。21教育网
4.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的倍,那么边长应缩小到原来的________倍。 21·cn·jy·com
5.已知与相似且面积比为4∶25,则与的相似比为 。
6.已知且,则= 。
7.在和中,,如果的周长是16,面积是12,那么的周长、面积依次为( )
A.8,3 B.8,6 C.4,3 D.4,6
8.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于( ) A. B. C. D.www.21-cn-jy.com
9.已知△ABC∽△DEF,且AB:DE=1:2,则△ABC的面积与△DEF的面积之比为( )2·1·c·n·j·y
A.1:2 B.1:4 C.2:1 D.4:1
10.两相似三角形的对应边的比为4:5,周长和为360cm,这两个三角形的周长分别是多少?
二.能力题
11.若△ABC∽△A′B′C′,AB=4,BC=5,AC=6,△A′B′C′的最大边长为15,那么它们的相似比是________,△A′B′C′的周长是________。
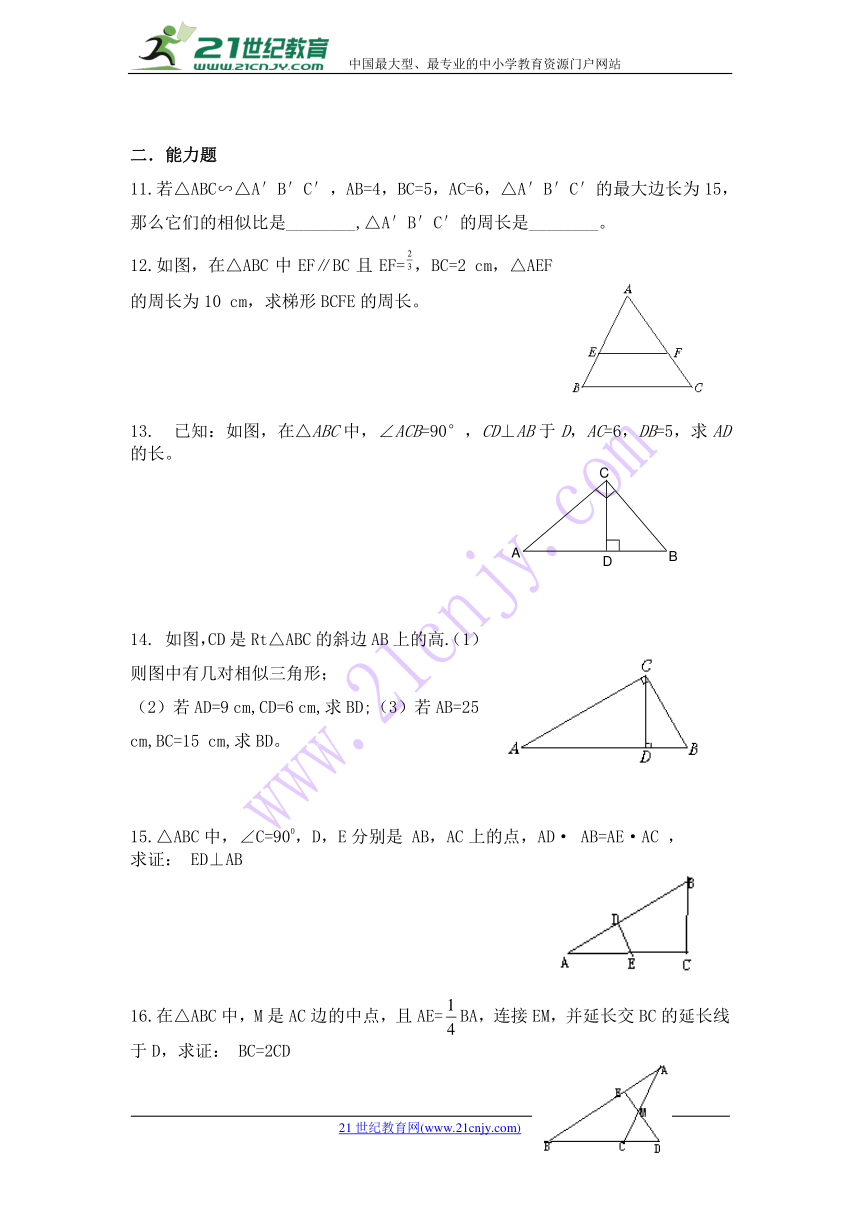
12.如图,在△ABC中EF∥BC且EF=,BC=2 cm,△AEF的周长为10 cm,求梯形BCFE的周长。【来源:21·世纪·教育·网】
13. 已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AC=6,DB=5,求AD的长。www-2-1-cnjy-com
14. 如图,CD是Rt△ABC的斜边AB上的高.(1)则图中有几对相似三角形;
(2)若AD=9 cm,CD=6 cm,求BD;(3)若AB=25 cm,BC=15 cm,求BD。2-1-c-n-j-y
15.△ABC中,∠C=900,D,E分别是 AB,AC上的点,AD· AB=AE·AC ,
求证: ED⊥AB
16.在△ABC中,M是AC边的中点,且AE=BA,连接EM,并延长交BC的延长线于D,求证: BC=2CD21*cnjy*com
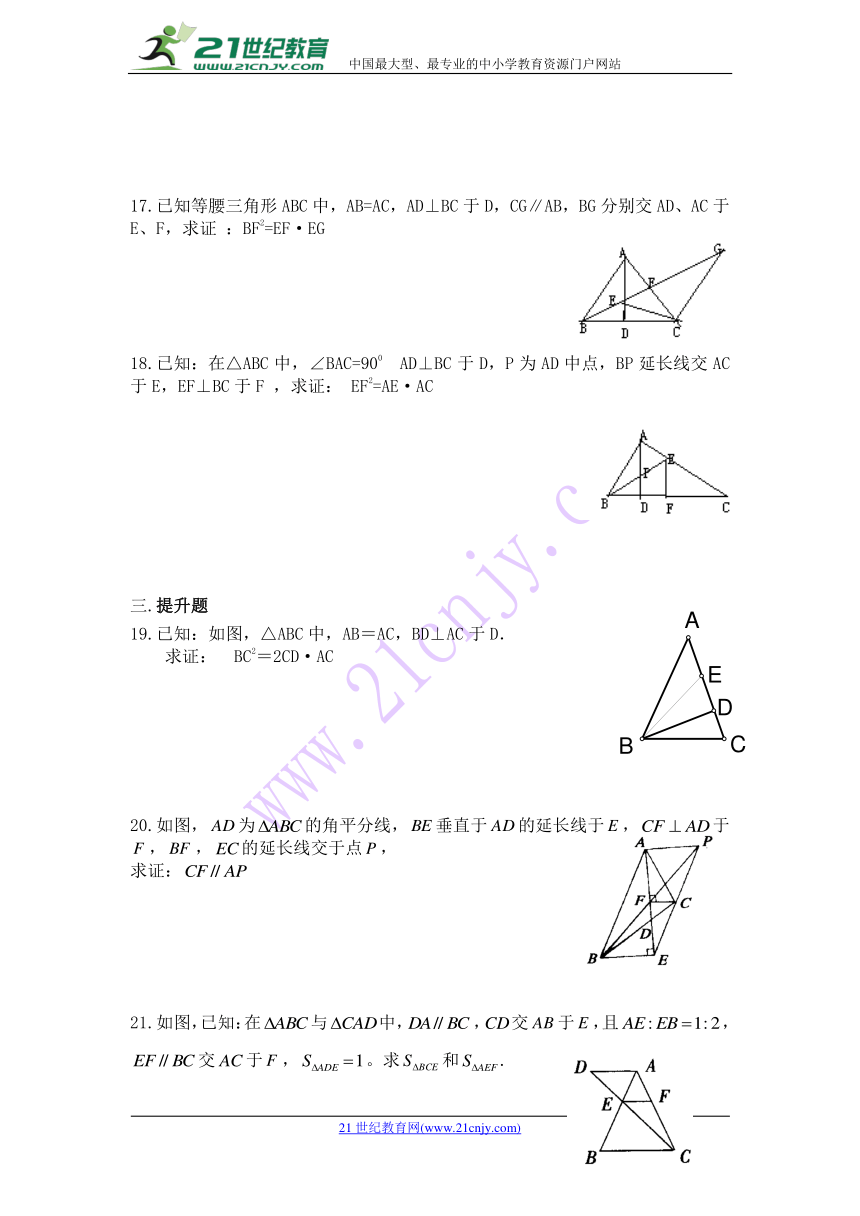
17.已知等腰三角形ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F,求证 :BF2=EF·EG【来源:21cnj*y.co*m】
18.已知:在△ABC中,∠BAC=900 AD⊥BC于D,P为AD中点,BP延长线交AC于E,EF⊥BC于F ,求证: EF2=AE·AC【出处:21教育名师】
三.提升题
19.已知:如图,△ABC中,AB=AC,BD⊥AC于D.
求证: BC2=2CD·AC
20.如图,为的角平分线,垂直于的延长线于,于,,的延长线交于点,
求证:
21.如图,已知:在与中,,交于,且,交于,。求和.
22.如图,△ABC中,AB=8,AC=6,BC=9.如果动点D以每秒2个单位长度的速度从点B出发沿边BA向点A运动,此时直线DE∥BC,交AC于点E。记x秒时DE的长度为y,请用含x的式子表示y.21·世纪*教育网
23.已知等腰直角三角形的面积为,它的内接矩形的一边在斜边上,且矩形的两边之比为5:2,求矩形的面积。21cnjy.com
答案解析:
1.因为△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,根据对应中线的比等于相似比,
2.根据对应角平分线的比、对应高的比等于相似比,可得对应高的比为 。
3.设大三角形的周长是x,根据周长比等于相似比可得,根据面积比等于相似比的平方可得两个三角形面积比为4∶9 。
4.根据面积比等于相似比的平方可得相似比为,所以边长应缩小到原来的倍。
5.根据相似三角形面积的比等于相似比的平方可求相似比为2:5。
6.根据相似三角形面积的比等于相似比的平方可求=。
7.根据相似三角形周长比等于相似比,面积比等于相似比的平方可得周长为8,面积为3,所以选A.
8.所以选D.
9.根据相似三角形面积的比等于相似比的平方可求,所以选B.
10.解: 因为相似三角形的周长比等于对应比,所以相似三角形的对应边是4比5,则周长比也是4比5。
设小三角形周长为A,大三角形周长为B
A:B=4:5
A=360÷(4+5)×4=160 cm
B=360÷(4+5)×5=200 cm
答:这两个三角形的周长分别是160 cm和200 cm.
11.2∶5 37.5
12.解∵EF=BC,∴,
∵EF∥BC ∴△AEF∽△ABC,,
∴,∴△ABC周长=15 (cm),
∴梯形BCF的周长=△ABC的周长-△AEF的周长+2EF=15-10+4=9 (cm)。
13.解:在△ACD和△ABC中,
∵∠A=∠A,∠ADC=∠ACB=90°,
∴△ACD∽△ABC.
∴.∴.
设AD=x,则AB=x+5,又AC=6,
∴.
解得:x=4(舍去负值)
∴AD=4.
14.(1)∵CD⊥AB,∴∠ADC=∠BDC=∠ACB=90°.
在△ADC和 △ACB中,∠ADC=∠ACB=90°,∠A=∠A,∴△ADC∽△ACB
同理可知,△CDB∽△ACB.∴△ADC∽△CDB.所以图中有三对相似三角形。
(2)∵△ACD∽△CBD,∴,即,∴BD=4 (cm).
(3)∵△CBD∽△ABC,∴.∴,∴BD==9 (cm).
15.证 △ADE∽△ACB ∠ADE=∠C=900 所以ED⊥AB
16.过点C作CF∥ED,交AB于F,易得F是AB中点,∴BF=2EF,又CF∥ED,∴,即 BC=2CD
17.先证BE=EC,∠EBC=∠ECB,可得∠ABF=∠ACF,又 AB∥CG,∴∠ABF=∠G,
∴△ECF∽△EGC,∴EC2=EF·EG ,即 BF2=EF·EG
18.延长BA、FE交于点G,由条件得AD∥FG,∴,,又AP=PD
∴EF=EG,再证△AEG∽△FEG,故 EF2=AE·EC
19.证明:如图,在AC截取DE=DC,
∵BD⊥AC于D,
∴BD是线段CE的垂直平分线,
∴BC=BE,∴∠C=∠BEC,
又∵ AB=AC,
∴∠C=∠ABC.
∴ △BCE∽△ACB.
∴, ∴
∴BC2=2CD·AC.
20.证明 ,,
,.
又,
∽
,
即.
21.解:,∽
又,
,
,∽
,
又∽,,
,与等高
22.解:经过x秒后,BD=2x,AD=8-2x.
∵DE∥BC,
∴△ADE∽△ABC.
∴,
即
∴
23.解:第一种情况:如图,中,,,内接矩形
由等腰直角三角形和矩形的性质,得
,
设为,则
由勾股定理得
矩形面积
第二种情况:如图所示的情况时,,同理可得
一.基础题
1.已知△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,且=,B′D′=4,则BD的长为 。21世纪教育网版权所有
2.已知△ABC∽△A′B′C′,AD和A′D′是它们的对应角平分线,且AD=8 cm, A′D′=3 cm.,则△ABC与△A′B′C′对应高的比为 。
3.两个相似三角形的相似比为2∶3,它们周长的差是25,那么较大三角形的周长是________,这两个三角形的面积比为 。21教育网
4.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的倍,那么边长应缩小到原来的________倍。 21·cn·jy·com
5.已知与相似且面积比为4∶25,则与的相似比为 。
6.已知且,则= 。
7.在和中,,如果的周长是16,面积是12,那么的周长、面积依次为( )
A.8,3 B.8,6 C.4,3 D.4,6
8.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O, 则等于( ) A. B. C. D.www.21-cn-jy.com
9.已知△ABC∽△DEF,且AB:DE=1:2,则△ABC的面积与△DEF的面积之比为( )2·1·c·n·j·y
A.1:2 B.1:4 C.2:1 D.4:1
10.两相似三角形的对应边的比为4:5,周长和为360cm,这两个三角形的周长分别是多少?
二.能力题
11.若△ABC∽△A′B′C′,AB=4,BC=5,AC=6,△A′B′C′的最大边长为15,那么它们的相似比是________,△A′B′C′的周长是________。
12.如图,在△ABC中EF∥BC且EF=,BC=2 cm,△AEF的周长为10 cm,求梯形BCFE的周长。【来源:21·世纪·教育·网】
13. 已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,AC=6,DB=5,求AD的长。www-2-1-cnjy-com
14. 如图,CD是Rt△ABC的斜边AB上的高.(1)则图中有几对相似三角形;
(2)若AD=9 cm,CD=6 cm,求BD;(3)若AB=25 cm,BC=15 cm,求BD。2-1-c-n-j-y
15.△ABC中,∠C=900,D,E分别是 AB,AC上的点,AD· AB=AE·AC ,
求证: ED⊥AB
16.在△ABC中,M是AC边的中点,且AE=BA,连接EM,并延长交BC的延长线于D,求证: BC=2CD21*cnjy*com
17.已知等腰三角形ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F,求证 :BF2=EF·EG【来源:21cnj*y.co*m】
18.已知:在△ABC中,∠BAC=900 AD⊥BC于D,P为AD中点,BP延长线交AC于E,EF⊥BC于F ,求证: EF2=AE·AC【出处:21教育名师】
三.提升题
19.已知:如图,△ABC中,AB=AC,BD⊥AC于D.
求证: BC2=2CD·AC
20.如图,为的角平分线,垂直于的延长线于,于,,的延长线交于点,
求证:
21.如图,已知:在与中,,交于,且,交于,。求和.
22.如图,△ABC中,AB=8,AC=6,BC=9.如果动点D以每秒2个单位长度的速度从点B出发沿边BA向点A运动,此时直线DE∥BC,交AC于点E。记x秒时DE的长度为y,请用含x的式子表示y.21·世纪*教育网
23.已知等腰直角三角形的面积为,它的内接矩形的一边在斜边上,且矩形的两边之比为5:2,求矩形的面积。21cnjy.com
答案解析:
1.因为△ABC∽△A′B′C′,BD和B′D′是它们的对应中线,根据对应中线的比等于相似比,
2.根据对应角平分线的比、对应高的比等于相似比,可得对应高的比为 。
3.设大三角形的周长是x,根据周长比等于相似比可得,根据面积比等于相似比的平方可得两个三角形面积比为4∶9 。
4.根据面积比等于相似比的平方可得相似比为,所以边长应缩小到原来的倍。
5.根据相似三角形面积的比等于相似比的平方可求相似比为2:5。
6.根据相似三角形面积的比等于相似比的平方可求=。
7.根据相似三角形周长比等于相似比,面积比等于相似比的平方可得周长为8,面积为3,所以选A.
8.所以选D.
9.根据相似三角形面积的比等于相似比的平方可求,所以选B.
10.解: 因为相似三角形的周长比等于对应比,所以相似三角形的对应边是4比5,则周长比也是4比5。
设小三角形周长为A,大三角形周长为B
A:B=4:5
A=360÷(4+5)×4=160 cm
B=360÷(4+5)×5=200 cm
答:这两个三角形的周长分别是160 cm和200 cm.
11.2∶5 37.5
12.解∵EF=BC,∴,
∵EF∥BC ∴△AEF∽△ABC,,
∴,∴△ABC周长=15 (cm),
∴梯形BCF的周长=△ABC的周长-△AEF的周长+2EF=15-10+4=9 (cm)。
13.解:在△ACD和△ABC中,
∵∠A=∠A,∠ADC=∠ACB=90°,
∴△ACD∽△ABC.
∴.∴.
设AD=x,则AB=x+5,又AC=6,
∴.
解得:x=4(舍去负值)
∴AD=4.
14.(1)∵CD⊥AB,∴∠ADC=∠BDC=∠ACB=90°.
在△ADC和 △ACB中,∠ADC=∠ACB=90°,∠A=∠A,∴△ADC∽△ACB
同理可知,△CDB∽△ACB.∴△ADC∽△CDB.所以图中有三对相似三角形。
(2)∵△ACD∽△CBD,∴,即,∴BD=4 (cm).
(3)∵△CBD∽△ABC,∴.∴,∴BD==9 (cm).
15.证 △ADE∽△ACB ∠ADE=∠C=900 所以ED⊥AB
16.过点C作CF∥ED,交AB于F,易得F是AB中点,∴BF=2EF,又CF∥ED,∴,即 BC=2CD
17.先证BE=EC,∠EBC=∠ECB,可得∠ABF=∠ACF,又 AB∥CG,∴∠ABF=∠G,
∴△ECF∽△EGC,∴EC2=EF·EG ,即 BF2=EF·EG
18.延长BA、FE交于点G,由条件得AD∥FG,∴,,又AP=PD
∴EF=EG,再证△AEG∽△FEG,故 EF2=AE·EC
19.证明:如图,在AC截取DE=DC,
∵BD⊥AC于D,
∴BD是线段CE的垂直平分线,
∴BC=BE,∴∠C=∠BEC,
又∵ AB=AC,
∴∠C=∠ABC.
∴ △BCE∽△ACB.
∴, ∴
∴BC2=2CD·AC.
20.证明 ,,
,.
又,
∽
,
即.
21.解:,∽
又,
,
,∽
,
又∽,,
,与等高
22.解:经过x秒后,BD=2x,AD=8-2x.
∵DE∥BC,
∴△ADE∽△ABC.
∴,
即
∴
23.解:第一种情况:如图,中,,,内接矩形
由等腰直角三角形和矩形的性质,得
,
设为,则
由勾股定理得
矩形面积
第二种情况:如图所示的情况时,,同理可得
