27.2.3相似的应用举例同步练(含答案)
文档属性
| 名称 | 27.2.3相似的应用举例同步练(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 599.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-29 16:51:44 | ||
图片预览



文档简介
《27.2.3相似的应用举例(1)》
【基础点拨】
1.在同一时刻同一个地点物体的高度与自身的影长的关系是( )
A.成反比例 B.成正比例 C.相等 D.不成比例
2.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( )21世纪教育网版权所有
A.15m B.60m C.20m D.
3.一斜坡长70m,它的高为5m,将某物从斜坡起点推到坡上20m处停止下,停下地点的高度为( )21教育网
A. B. C. D.
4.如图2,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为( )21·cn·jy·com
A. B. C. D.
图1 图2 图3
5.如图2所示阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐距地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5m B.1.6m C.1.86m D.2.16m
6.如图3所示,AB是斜靠在墙壁上的长梯,梯脚B距离墙角1.6m,梯上点D距离墙1.4m,BD长0.55m,则梯子长为( )www.21-cn-jy.com
A.3.85m B.4.00m C.4.40m D.4.50m
7.已知A,B两地相距300 km,在地图上量得两地相距15 cm,则图上距离与实际距离之比为___________。2·1·c·n·j·y
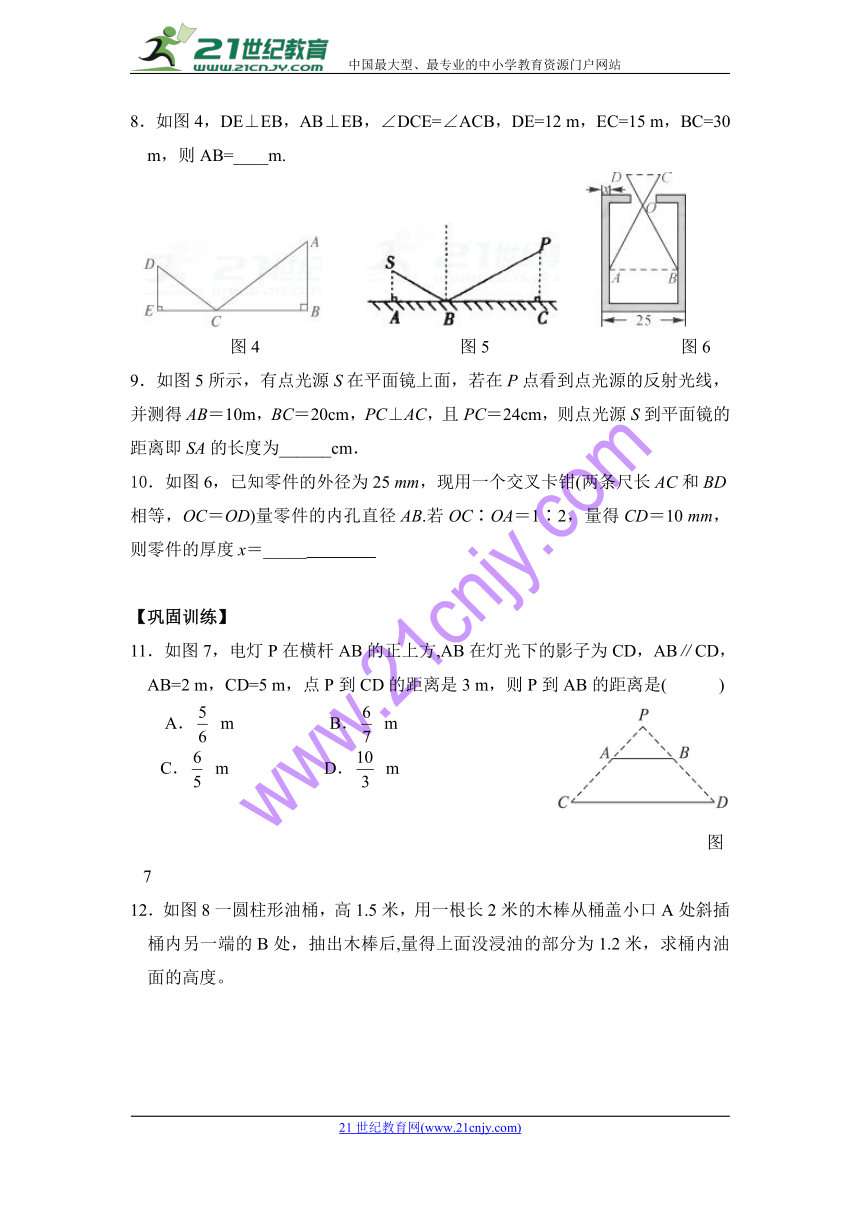
8.如图4,DE⊥EB,AB⊥EB,∠DCE=∠ACB,DE=12 m,EC=15 m,BC=30 m,则AB=____m.【来源:21·世纪·教育·网】
图4 图5 图6
9.如图5所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10m,BC=20cm,PC⊥AC,且PC=24cm,则点光源S到平面镜的距离即SA的长度为______cm.21·世纪*教育网
10.如图6,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x=_____ 2-1-c-n-j-y
【巩固训练】
11.如图7,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,点P到CD的距离是3 m,则P到AB的距离是( )
A. m B. m
C. m D. m
图7
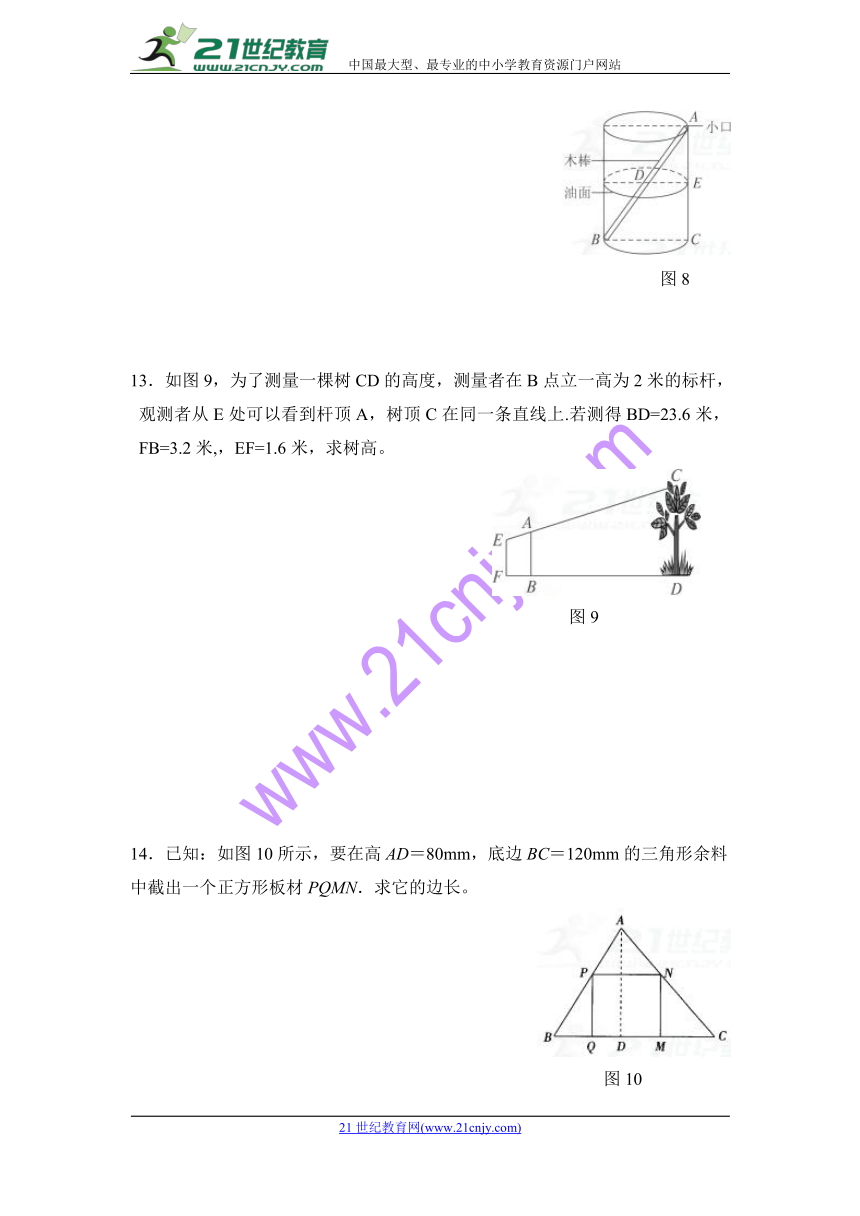
12.如图8一圆柱形油桶,高1.5米,用一根长2米的木棒从桶盖小口A处斜插桶内另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2米,求桶内油面的高度。【来源:21cnj*y.co*m】
图8
13.如图9,为了测量一棵树CD的高度,测量者在B点立一高为2米的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上.若测得BD=23.6米,FB=3.2米,,EF=1.6米,求树高。【出处:21教育名师】
图9
14.已知:如图10所示,要在高AD=80mm,底边BC=120mm的三角形余料中截出一个正方形板材PQMN.求它的边长。【版权所有:21教育】
图10
【能力提升】
15.如图11,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B. 减小1.5米
C. 增大3.5米 D. 减小3.5米
图11
16.晨晓想用镜子测量一棵古松树的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图12,第一次他把镜子放在C点,人在F点正好看到树尖A;第二次他把镜子放在C′处,人在F′处正好看到树尖A,已知晨晓眼睛距地面1.70 m,量得CC′为12 m,CF长1.8 m,C′F′为3.84 m,求这棵古松树的高。21cnjy.com
图12
【参考答案】
B; 2.A; 3.B; 4.A; 5.A; 6.C; 7.1:2000000; 8.24; 9.12; 10.2.5mm; 11.C;www-2-1-cnjy-com
12. 解:根据题意建立数学模型,如右图,AD=1.2米,AB=2米,,AC=1.5米,DE∥BC.21*cnjy*com
∵DE∥BC,∴∠ADE=∠B,
∠AED=∠C.
∴△ADE∽△ABC.
∴.∴
∴AE=0.9(米).
∴EC=AC-AE=1.5-0.9=0.6(米).
13. 解:由题意得△AEM∽△CEN,
∴.而AM=0.4,EM=3.2,
EN=26.8,
∴CN=3.35.
∴CD=4.95(米).
答:树高4.95米。
14.解:设正方形的边长为x,
∵四边形PQMN是正方形,∴PN∥BC,
∴△APN∽△ABC,
∴,即
解得x=48,
所以,加工后正方形的边长为48mm.
15.D.提示:小明在不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化。
16.解:设BC=y m,AB=x m,作CM⊥BF,C′M′⊥BF′.
由物理学中光的反射定理,得∠ACM=∠ECM,∠AC′M′=∠E′C′M′,
所以∠ACB=∠ECF,∠AC′B=∠E′C′F′。
因为 ∠ABC=∠EFC=90°,∠ABC=∠E′F′C′=90°,
所以△ABC∽△EFC,△ABC′∽△E′F′C′.所以。
所以,①
.②
解①②组成的方程组,得
所以这棵古松树的高为10米。
《27.2.3相似的应用举例(2)》
【基础点拨】
1.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为( )
A. B.1 C. D..
第1题图 第2题图 第3题图
2.如图,某一时刻,测得旗杆的影长为8 m,李明测得小芳的影长为1 m,已知小芳的身高为1.5 m,则旗杆的高度是 m.
3.如图,已知有两堵墙AB、CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外。将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为 。
4.如图是小玲设计的用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米。那么该古城墙CD的高_______米。
第4题图
5.在一次数学活动课上,李老师带领学生去测教学楼的高度,在阳光下,测得身高为1.65m的黄丽同学BC的影长BA为1.1m,与此同时,测得教学楼DE的影长DF为12.1m,如图所示,请你根据已测得的数据,测出教学楼DE的高度。(精确到0.1m)
第5题图
【巩固训练】
6.如图,一油桶高0.8 m,桶内有油,一根木棒长1 m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8 m,
则桶内油的高度为______。
第6题图
7.一人拿着一个刻有厘米分度的小尺,站在距离电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上的12个分度恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高。
8.一条河的两岸有一段是平行的,在河的这岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这一岸离开岸边25米处看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽。
9.一位同学想利用树影测量树高AB,他在某一时刻测得小树高为1米,树影长0.9米,但当他马上测量树影时,因树靠近建筑物,影子不全落在地上,有一部分落在墙上,如图,他先测得地面部分的影子长2.7米,又测得墙上的影高CD为1.2米,试问树有多高?
【能力提升】
10.如图,小华在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小华的身高是1.60m,两个路灯的高度都是9.6m,设AP =x(m)。 (1)求两路灯之间的距离; (2)当小华走到路灯B时,他在路灯下的影子是多少?
11.某高中学校为高一新生设计的学生板凳如图所示.其中BA=CD,BC=20 cm,BC、EF平行于地面AD且到地面AD的距离分别为40 cm、8 cm,为使板凳两腿底端A,D之间的距离为50 cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计)
【参考答案】
1.C 2.12 3.7.5m 4.8m
5. 解∵EF∥AC,∴∠CAB=∠EFD.
又∠CBA=∠EDF=90°,∴△ABC∽△FDE.
故教学楼的高度约为18.2m.
6.0.64m
7.解:设电线杆高x m,因为两三角形相似,
则有,解得x=6,
经检验x=6为原分式方程的根,所以电线杆高6 m。
8.解:根据题意,画出图形,其中AB=50米,CD=5×4=20米,GE⊥CD,GF⊥AB,点G、E、F共线,GE=25米。
∵AB∥CD,∴∠DCG=∠BAG,∠CDG=∠ABG.
∴△GCD∽△GAB.
又∵GE⊥CD,GF⊥AB,
∴(相似三角形对应高的比等于相似比)。
∴GF==62.5(米).
∴河宽EF=GF-GE=62.5-25=37.5(米).
9.解:延长AD、BE相交于点C,则CE就是树影长的一部分,
,即.∴CE=1.08 (m).
∴BC=BE+EC=2.7+1.08=3.78 (m).
∴,即.∴AB=4.2 (m).
10.解:由题意知: PQ=12米,AC=BD=9.6米,MP=NQ=1.6米,AP=QB,
在△APM和△ABD中,∵∠DAB是公共角,∠APM=∠ABD=90°,
∴△AMP∽△ADB,∴,即,解得AB=18.
答:两个路灯之间的距离是18米。
11.解:过点C作CM∥AB,分别交EF,AD于N,M,作CP⊥AD,分别交EF,AD于Q,P.
由题意,得四边形ABCM,EBCN是平行四边形,
∴EN=AM=BC=20 cm.
∴MD=AD-AM=50-20=30(cm).
由题意知CP=40 cm,PQ=8 cm,
∴CQ=32 cm.
∵EF∥AD,∴△CNF∽△CMD.
∴=,即=.
∴NF=24 cm.
∴EF=EN+NF=20+24=44(cm).
答:横梁EF应为44 cm.
【基础点拨】
1.在同一时刻同一个地点物体的高度与自身的影长的关系是( )
A.成反比例 B.成正比例 C.相等 D.不成比例
2.已知一棵树的影长是30m,同一时刻一根长1.5m的标杆的影长为3m,则这棵树的高度是( )21世纪教育网版权所有
A.15m B.60m C.20m D.
3.一斜坡长70m,它的高为5m,将某物从斜坡起点推到坡上20m处停止下,停下地点的高度为( )21教育网
A. B. C. D.
4.如图2,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D、E,若AD=4,DB=2,则DE∶BC的值为( )21·cn·jy·com
A. B. C. D.
图1 图2 图3
5.如图2所示阳光从教室的窗户射入室内,窗户框AB在地面上的影长DE=1.8m,窗户下檐距地面的距离BC=1m,EC=1.2m,那么窗户的高AB为( )
A.1.5m B.1.6m C.1.86m D.2.16m
6.如图3所示,AB是斜靠在墙壁上的长梯,梯脚B距离墙角1.6m,梯上点D距离墙1.4m,BD长0.55m,则梯子长为( )www.21-cn-jy.com
A.3.85m B.4.00m C.4.40m D.4.50m
7.已知A,B两地相距300 km,在地图上量得两地相距15 cm,则图上距离与实际距离之比为___________。2·1·c·n·j·y
8.如图4,DE⊥EB,AB⊥EB,∠DCE=∠ACB,DE=12 m,EC=15 m,BC=30 m,则AB=____m.【来源:21·世纪·教育·网】
图4 图5 图6
9.如图5所示,有点光源S在平面镜上面,若在P点看到点光源的反射光线,并测得AB=10m,BC=20cm,PC⊥AC,且PC=24cm,则点光源S到平面镜的距离即SA的长度为______cm.21·世纪*教育网
10.如图6,已知零件的外径为25 mm,现用一个交叉卡钳(两条尺长AC和BD相等,OC=OD)量零件的内孔直径AB.若OC∶OA=1∶2,量得CD=10 mm,则零件的厚度x=_____ 2-1-c-n-j-y
【巩固训练】
11.如图7,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB∥CD,AB=2 m,CD=5 m,点P到CD的距离是3 m,则P到AB的距离是( )
A. m B. m
C. m D. m
图7
12.如图8一圆柱形油桶,高1.5米,用一根长2米的木棒从桶盖小口A处斜插桶内另一端的B处,抽出木棒后,量得上面没浸油的部分为1.2米,求桶内油面的高度。【来源:21cnj*y.co*m】
图8
13.如图9,为了测量一棵树CD的高度,测量者在B点立一高为2米的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上.若测得BD=23.6米,FB=3.2米,,EF=1.6米,求树高。【出处:21教育名师】
图9
14.已知:如图10所示,要在高AD=80mm,底边BC=120mm的三角形余料中截出一个正方形板材PQMN.求它的边长。【版权所有:21教育】
图10
【能力提升】
15.如图11,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度( )
A.增大1.5米 B. 减小1.5米
C. 增大3.5米 D. 减小3.5米
图11
16.晨晓想用镜子测量一棵古松树的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,如图12,第一次他把镜子放在C点,人在F点正好看到树尖A;第二次他把镜子放在C′处,人在F′处正好看到树尖A,已知晨晓眼睛距地面1.70 m,量得CC′为12 m,CF长1.8 m,C′F′为3.84 m,求这棵古松树的高。21cnjy.com
图12
【参考答案】
B; 2.A; 3.B; 4.A; 5.A; 6.C; 7.1:2000000; 8.24; 9.12; 10.2.5mm; 11.C;www-2-1-cnjy-com
12. 解:根据题意建立数学模型,如右图,AD=1.2米,AB=2米,,AC=1.5米,DE∥BC.21*cnjy*com
∵DE∥BC,∴∠ADE=∠B,
∠AED=∠C.
∴△ADE∽△ABC.
∴.∴
∴AE=0.9(米).
∴EC=AC-AE=1.5-0.9=0.6(米).
13. 解:由题意得△AEM∽△CEN,
∴.而AM=0.4,EM=3.2,
EN=26.8,
∴CN=3.35.
∴CD=4.95(米).
答:树高4.95米。
14.解:设正方形的边长为x,
∵四边形PQMN是正方形,∴PN∥BC,
∴△APN∽△ABC,
∴,即
解得x=48,
所以,加工后正方形的边长为48mm.
15.D.提示:小明在不同的位置时,均可构成两个相似三角形,可利用相似比求人影长度的变化。
16.解:设BC=y m,AB=x m,作CM⊥BF,C′M′⊥BF′.
由物理学中光的反射定理,得∠ACM=∠ECM,∠AC′M′=∠E′C′M′,
所以∠ACB=∠ECF,∠AC′B=∠E′C′F′。
因为 ∠ABC=∠EFC=90°,∠ABC=∠E′F′C′=90°,
所以△ABC∽△EFC,△ABC′∽△E′F′C′.所以。
所以,①
.②
解①②组成的方程组,得
所以这棵古松树的高为10米。
《27.2.3相似的应用举例(2)》
【基础点拨】
1.如图,小明在打网球时,使球恰好能打过网,而且落点恰好在离网6米的位置上,则球拍击球的高度h为( )
A. B.1 C. D..
第1题图 第2题图 第3题图
2.如图,某一时刻,测得旗杆的影长为8 m,李明测得小芳的影长为1 m,已知小芳的身高为1.5 m,则旗杆的高度是 m.
3.如图,已知有两堵墙AB、CD,AB墙高2米,两墙之间的距离BC为8米,小明将一架木梯放在距B点3米的E处靠向墙AB时,木梯有很多露出墙外。将木梯绕点E旋转90°靠向墙CD时,木梯刚好达到墙的顶端,则墙CD的高为 。
4.如图是小玲设计的用手电来测量某古城墙高度的示意图.在点P处放一水平的平面镜,光线从点A出发经平面镜反射后,刚好射到古城墙CD的顶端C处.已知AB⊥BD,CD⊥BD,且测得AB=1.4米,BP=2.1米,PD=12米。那么该古城墙CD的高_______米。
第4题图
5.在一次数学活动课上,李老师带领学生去测教学楼的高度,在阳光下,测得身高为1.65m的黄丽同学BC的影长BA为1.1m,与此同时,测得教学楼DE的影长DF为12.1m,如图所示,请你根据已测得的数据,测出教学楼DE的高度。(精确到0.1m)
第5题图
【巩固训练】
6.如图,一油桶高0.8 m,桶内有油,一根木棒长1 m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8 m,
则桶内油的高度为______。
第6题图
7.一人拿着一个刻有厘米分度的小尺,站在距离电线杆约30米的地方,把手臂向前伸直,小尺竖直,看到尺上的12个分度恰好遮住电线杆,已知手臂长约60厘米,求电线杆的高。
8.一条河的两岸有一段是平行的,在河的这岸每隔5米有一棵树,在河的对岸每隔50米有一根电线杆,在这一岸离开岸边25米处看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽。
9.一位同学想利用树影测量树高AB,他在某一时刻测得小树高为1米,树影长0.9米,但当他马上测量树影时,因树靠近建筑物,影子不全落在地上,有一部分落在墙上,如图,他先测得地面部分的影子长2.7米,又测得墙上的影高CD为1.2米,试问树有多高?
【能力提升】
10.如图,小华在晚上由路灯A走向路灯B,当他走到点P时,发现他身后影子的顶部刚好接触到路灯A的底部,当他向前再步行12m到达点Q时,发现他身前影子的顶部刚好接触到路灯B的底部,已知小华的身高是1.60m,两个路灯的高度都是9.6m,设AP =x(m)。 (1)求两路灯之间的距离; (2)当小华走到路灯B时,他在路灯下的影子是多少?
11.某高中学校为高一新生设计的学生板凳如图所示.其中BA=CD,BC=20 cm,BC、EF平行于地面AD且到地面AD的距离分别为40 cm、8 cm,为使板凳两腿底端A,D之间的距离为50 cm,那么横梁EF应为多长?(材质及其厚度等暂忽略不计)
【参考答案】
1.C 2.12 3.7.5m 4.8m
5. 解∵EF∥AC,∴∠CAB=∠EFD.
又∠CBA=∠EDF=90°,∴△ABC∽△FDE.
故教学楼的高度约为18.2m.
6.0.64m
7.解:设电线杆高x m,因为两三角形相似,
则有,解得x=6,
经检验x=6为原分式方程的根,所以电线杆高6 m。
8.解:根据题意,画出图形,其中AB=50米,CD=5×4=20米,GE⊥CD,GF⊥AB,点G、E、F共线,GE=25米。
∵AB∥CD,∴∠DCG=∠BAG,∠CDG=∠ABG.
∴△GCD∽△GAB.
又∵GE⊥CD,GF⊥AB,
∴(相似三角形对应高的比等于相似比)。
∴GF==62.5(米).
∴河宽EF=GF-GE=62.5-25=37.5(米).
9.解:延长AD、BE相交于点C,则CE就是树影长的一部分,
,即.∴CE=1.08 (m).
∴BC=BE+EC=2.7+1.08=3.78 (m).
∴,即.∴AB=4.2 (m).
10.解:由题意知: PQ=12米,AC=BD=9.6米,MP=NQ=1.6米,AP=QB,
在△APM和△ABD中,∵∠DAB是公共角,∠APM=∠ABD=90°,
∴△AMP∽△ADB,∴,即,解得AB=18.
答:两个路灯之间的距离是18米。
11.解:过点C作CM∥AB,分别交EF,AD于N,M,作CP⊥AD,分别交EF,AD于Q,P.
由题意,得四边形ABCM,EBCN是平行四边形,
∴EN=AM=BC=20 cm.
∴MD=AD-AM=50-20=30(cm).
由题意知CP=40 cm,PQ=8 cm,
∴CQ=32 cm.
∵EF∥AD,∴△CNF∽△CMD.
∴=,即=.
∴NF=24 cm.
∴EF=EN+NF=20+24=44(cm).
答:横梁EF应为44 cm.
