4.5.1垂线-同步练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.5.1 垂线
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一、选择题:(本大题5个小题,每小题6分,共30分)
1.同学们,你一定练过跳远吧!在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线( )
A.平行 B.垂直 C.成45° D.以上都不对
2.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
A.互相垂直 B.互相平行
C.既不垂直也不平行 D.不能确定
3.如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是( )
A.20o B.30o C.40o D.50o
4.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有( )
A.① B.①②③ C.①④ D.②③④
二、填空题(本大题5个小题,每小题6分,共30分)
5.已知α=80°,β的两边与α的两边分别垂直,则β等于 .
6.在同一平面内,若a⊥b,a⊥c,则b与c的位置关系是 .
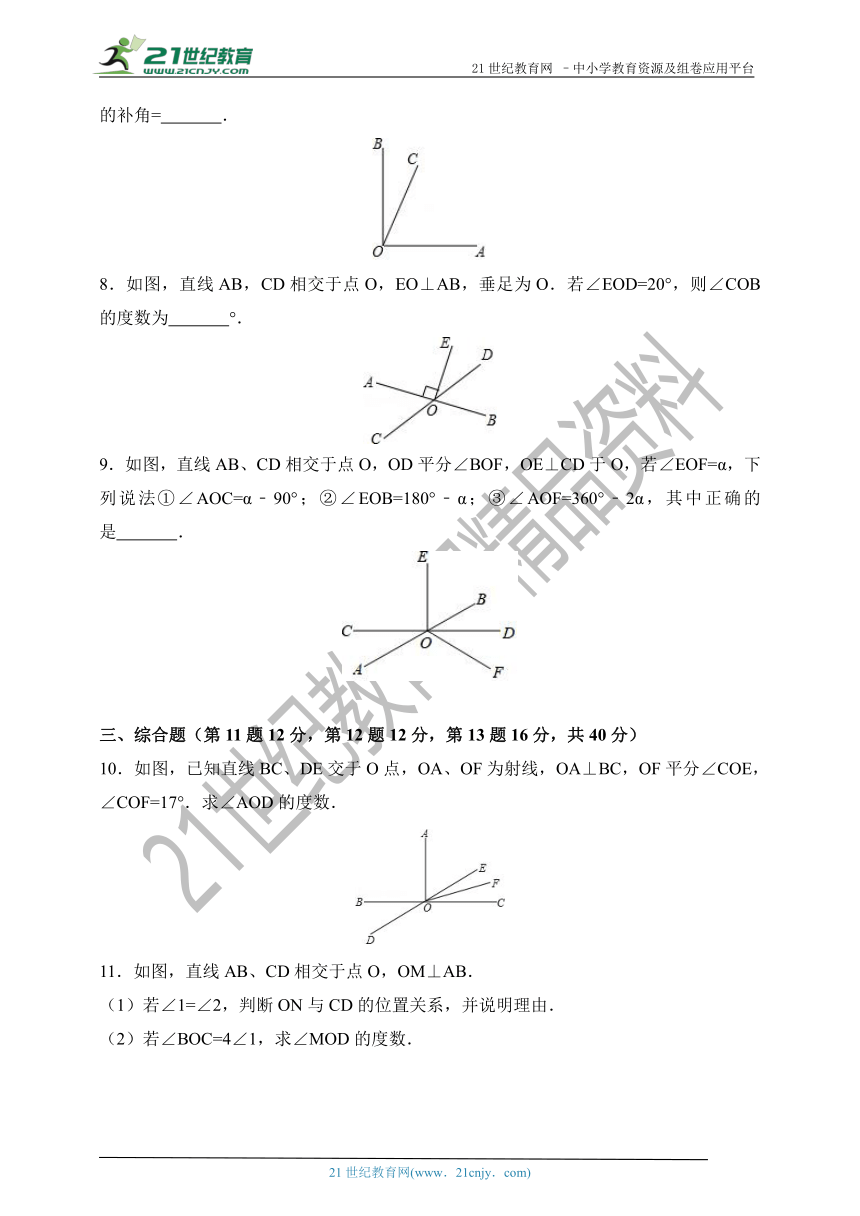
7.如图,BO⊥AO,∠BOC与∠BOA的度数之比为1:5,那么∠COA= ,∠BOC的补角= .21世纪教育网
8.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=20°,则∠COB的度数为 °.21·cn·jy·com
9.如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是 .www.21-cn-jy.com
三、综合题(第11题12分,第12题12分,第13题16分,共40分)
10.如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.【21·世纪·教育·网】
11.如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由.
(2)若∠BOC=4∠1,求∠MOD的度数.
12.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°.
①那么根据 ,可得∠BOC= 度.
②因为OP是∠BOC的平分线,所以∠COP=∠ = 度.
③求∠BOF的度数.
试题解析
一.选择题
1.B
【分析】根据点到直线的距离的定义解答即可.
【解答】解:∵点到直线的垂线段的长叫点到直线的距离,
∴在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线垂直.
故选:B.
【点评】此题比较简单,解答此题的关键是熟知点到直线距离的定义.
2.A
【分析】∠A与∠B是对顶角且互补,根据对顶角的性质,判断这两个对顶角相等,且都为90°,因此它们两边所在的直线互相垂直.21教育网
【解答】解:∵∠A与∠B是对顶角,
∴∠A=∠B,
又∵∠A与∠B互补,
∴∠A+∠B=180°,
可求∠A=90°.
故选:A.
【点评】本题考查垂线的定义和对顶角的性质,是简单的基础题.
3.A
【分析】根据垂线的定义,可得∠AOB,根据角的和差,可得∠AOC,根据角平分线的定义,可得∠COD,根据角的和差,可得答案.21cnjy.com
【解答】解:∵OA⊥OB,
∴∠AOB=90°,
∵∠AOC=∠AOB+∠BOC,∠BOC=50°,
∴∠AOC=50°+90°=140°.
∵OD平分∠AOC,
∴∠COD=∠AOC=×140°=70°.
∵∠BOD=∠COD﹣∠BOC=70°﹣50°=20°,
故选:A.
【点评】本题考查了垂线,利用角的和差是解题关键.
4.C
【分析】根据垂直定义可得∠BCA=90°,∠ADC=∠BDC=∠ACF=90°,然后再根据余角定义和补角定义进行分析即可.2·1·c·n·j·y
【解答】解:∵AC⊥BF,
∴∠BCA=90°,
∴∠ACD+∠1=90°,
∴∠1是∠ACD的余角,故①正确;
∵CD⊥BE,
∴∠ADC=∠CDB=90°,
∴∠B+∠BCD=90°,∠ACD+∠DAC=90°,
∵∠BCA=90°,
∴∠B+∠BAC=90°,∠1+∠ACD=90°,
∴图中互余的角共有4对,故②错误;
∵∠1+∠DCF=180°,
∴∠1的补角是∠DCF,
∵∠1+∠DCA=90°,∠DAC+∠DCA=90°,
∴∠1=∠DAC,
∵∠DAC+∠CAE=180°,
∴∠1+∠CAE=180°,
∴∠1的补角有∠CAE,故③说法错误;
∵∠ACB=90°,∠ACF=90°,∠ADC=∠BDC=90°,
∴∠BDC,∠ACB,∠ACF和∠ADC互补,故④说法正确.
正确的是①④;
故选:C.
【点评】此题主要考查了余角和补角,关键是掌握两角之和为90°时,这两个角互余,两角之和为180°时,这两个角互补.21·世纪*教育网
二.填空题
5. 80°或100° .
【分析】若两个角的边互相垂直,那么这两个角必相等或互补,可据此解答.
【解答】解:∵β的两边与α的两边分别垂直,
∴α+β=180°,
故β=100°,
在上述情况下,若反向延长∠β的一边,那么∠β的补角的两边也与∠α的两边互相垂直,故此时∠β=180°﹣100°=80°;2-1-c-n-j-y
综上可知:∠β=80°或100°,
故答案为80°或100°.
【点评】本题主要考查角的概念的知识点,要注意从不同的角度来分析∠β的存在情况,以免漏解.
6. 平行 .
【分析】根据垂直定义得出∠CMB=∠ENB=90°,根据平行线的判定求出即可.
【解答】解:∵CD⊥AB,EF⊥AB,
∴∠CMB=∠ENB=90°,
∴CD∥EF.
故答案为:平行.
【点评】本题主要考查对垂线,平行线的判定等知识点的理解和掌握,能求出∠CMB=∠ENB=90°是解此题的关键.21*cnjy*com
7. 162° .
【分析】直接利用垂直的定义结合,∠BOC与∠BOA的度数之比得出答案.
【解答】解:∵BO⊥AO,∠BOC与∠BOA的度数之比为1:5,
∴∠COA=×90°=72°,
则∠BOC=18°,
故∠BOC的补角=180°﹣18°=162°.
故答案为:72°,162°.
【点评】此题主要考查了垂直的定义以及互补的定义,正确得出∠COA的度数是解题关键.
8. 110 °.
【分析】先根据垂直的定义求出∠BOE=90°,然后求出∠BOD的度数,再根据对顶角相等求出∠AOC的度数,再根据邻补角的定义求出∠COB的度数.【21cnj*y.co*m】
【解答】解:∵OE⊥AB,
∴∠BOE=90°,
∵∠EOD=20°,
∴∠BOD=∠BOE﹣∠EOD=90°﹣20°=70°,
∴∠COB=180°﹣∠BOD=180°﹣70°=110°.
故答案为:110.
【点评】本题考查了垂线的定义,对顶角相等,邻补角的和等于180°,要注意领会由垂直得直角这一要点.
9. ①②③ .
【分析】根据垂线、角之间的和与差,即可解答.
【解答】解:∵OE⊥CD于O,∠EOF=α,
∴∠DOF=α﹣90°,
∵OD平分∠BOF,
∴∠BOD=∠FOD,
∵∠AOC=∠BOD,
∴∠AOC=∠FOD,
∴∠AOC=α﹣90°,①正确;
∴∠BOE=180°﹣∠COE﹣∠AOC=180°﹣90°﹣(α﹣90°)=180°﹣α,②正确;
∴∠AOF=180°﹣∠AOC﹣∠DOF=180°﹣(α﹣90°)﹣(α﹣90°)=360°﹣2α,③正确;
故答案为:①②③
【点评】本题考查了垂线,解决本题的关键是利用角之间的关系解答.
三.综合题
10.【分析】直接利用角平分线的定义得出∠EOC=34°,再利用对顶角的定义得出∠BOD的度数,进而得出答案.www-2-1-cnjy-com
【解答】解:∵OF平分∠COE,
∴∠EOF=∠FOC=17°,
∴∠EOC=34°,
∴∠BOD=34°,
∵OA⊥BC,
∴∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+34°=124°.
【点评】此题主要考查了垂线的定义以及角平分线的定义,正确得出∠BOD的度数是解题关键.
11.【分析】(1)根据垂直定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,再利用等量代换可得到∠2+∠AOC=90°,从而可得ON⊥CD;【21教育名师】
(2)根据垂直定义和条件可得∠1=30°,∠BOC=120°,再根据邻补角定义可得∠MOD的度数.
【解答】解:(1)ON⊥CD.
理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
又∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
(2)∵OM⊥AB,∠BOC=4∠1,
∴∠1=30°,∠BOC=120°,
又∵∠1+∠MOD=180°,
∴∠MOD=180°﹣∠1=150°.
【点评】此题主要垂直定义,关键是掌握垂线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.5.1 垂线
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一、选择题:(本大题5个小题,每小题6分,共30分)
1.同学们,你一定练过跳远吧!在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线( )
A.平行 B.垂直 C.成45° D.以上都不对
2.若∠A与∠B是对顶角且互补,则它们两边所在的直线( )
A.互相垂直 B.互相平行
C.既不垂直也不平行 D.不能确定
3.如图,OA⊥OB,∠BOC=50°,OD平分∠AOC,则∠BOD的度数是( )
A.20o B.30o C.40o D.50o
4.如图,已知点A是射线BE上一点,过A作AC⊥BF,垂足为C,CD⊥BE,垂足为D.给出下列结论:①∠1是∠ACD的余角;②图中互余的角共有3对;③∠1的补角只有∠DCF;④与∠ADC互补的角共有3个.其中正确结论有( )
A.① B.①②③ C.①④ D.②③④
二、填空题(本大题5个小题,每小题6分,共30分)
5.已知α=80°,β的两边与α的两边分别垂直,则β等于 .
6.在同一平面内,若a⊥b,a⊥c,则b与c的位置关系是 .
7.如图,BO⊥AO,∠BOC与∠BOA的度数之比为1:5,那么∠COA= ,∠BOC的补角= .21世纪教育网
8.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.若∠EOD=20°,则∠COB的度数为 °.21·cn·jy·com
9.如图,直线AB、CD相交于点O,OD平分∠BOF,OE⊥CD于O,若∠EOF=α,下列说法①∠AOC=α﹣90°;②∠EOB=180°﹣α;③∠AOF=360°﹣2α,其中正确的是 .www.21-cn-jy.com
三、综合题(第11题12分,第12题12分,第13题16分,共40分)
10.如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.【21·世纪·教育·网】
11.如图,直线AB、CD相交于点O,OM⊥AB.
(1)若∠1=∠2,判断ON与CD的位置关系,并说明理由.
(2)若∠BOC=4∠1,求∠MOD的度数.
12.如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.
(1)图中除直角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°.
①那么根据 ,可得∠BOC= 度.
②因为OP是∠BOC的平分线,所以∠COP=∠ = 度.
③求∠BOF的度数.
试题解析
一.选择题
1.B
【分析】根据点到直线的距离的定义解答即可.
【解答】解:∵点到直线的垂线段的长叫点到直线的距离,
∴在测量跳远成绩时,从落地点拉向起跳线的皮尺,应当与起跳线垂直.
故选:B.
【点评】此题比较简单,解答此题的关键是熟知点到直线距离的定义.
2.A
【分析】∠A与∠B是对顶角且互补,根据对顶角的性质,判断这两个对顶角相等,且都为90°,因此它们两边所在的直线互相垂直.21教育网
【解答】解:∵∠A与∠B是对顶角,
∴∠A=∠B,
又∵∠A与∠B互补,
∴∠A+∠B=180°,
可求∠A=90°.
故选:A.
【点评】本题考查垂线的定义和对顶角的性质,是简单的基础题.
3.A
【分析】根据垂线的定义,可得∠AOB,根据角的和差,可得∠AOC,根据角平分线的定义,可得∠COD,根据角的和差,可得答案.21cnjy.com
【解答】解:∵OA⊥OB,
∴∠AOB=90°,
∵∠AOC=∠AOB+∠BOC,∠BOC=50°,
∴∠AOC=50°+90°=140°.
∵OD平分∠AOC,
∴∠COD=∠AOC=×140°=70°.
∵∠BOD=∠COD﹣∠BOC=70°﹣50°=20°,
故选:A.
【点评】本题考查了垂线,利用角的和差是解题关键.
4.C
【分析】根据垂直定义可得∠BCA=90°,∠ADC=∠BDC=∠ACF=90°,然后再根据余角定义和补角定义进行分析即可.2·1·c·n·j·y
【解答】解:∵AC⊥BF,
∴∠BCA=90°,
∴∠ACD+∠1=90°,
∴∠1是∠ACD的余角,故①正确;
∵CD⊥BE,
∴∠ADC=∠CDB=90°,
∴∠B+∠BCD=90°,∠ACD+∠DAC=90°,
∵∠BCA=90°,
∴∠B+∠BAC=90°,∠1+∠ACD=90°,
∴图中互余的角共有4对,故②错误;
∵∠1+∠DCF=180°,
∴∠1的补角是∠DCF,
∵∠1+∠DCA=90°,∠DAC+∠DCA=90°,
∴∠1=∠DAC,
∵∠DAC+∠CAE=180°,
∴∠1+∠CAE=180°,
∴∠1的补角有∠CAE,故③说法错误;
∵∠ACB=90°,∠ACF=90°,∠ADC=∠BDC=90°,
∴∠BDC,∠ACB,∠ACF和∠ADC互补,故④说法正确.
正确的是①④;
故选:C.
【点评】此题主要考查了余角和补角,关键是掌握两角之和为90°时,这两个角互余,两角之和为180°时,这两个角互补.21·世纪*教育网
二.填空题
5. 80°或100° .
【分析】若两个角的边互相垂直,那么这两个角必相等或互补,可据此解答.
【解答】解:∵β的两边与α的两边分别垂直,
∴α+β=180°,
故β=100°,
在上述情况下,若反向延长∠β的一边,那么∠β的补角的两边也与∠α的两边互相垂直,故此时∠β=180°﹣100°=80°;2-1-c-n-j-y
综上可知:∠β=80°或100°,
故答案为80°或100°.
【点评】本题主要考查角的概念的知识点,要注意从不同的角度来分析∠β的存在情况,以免漏解.
6. 平行 .
【分析】根据垂直定义得出∠CMB=∠ENB=90°,根据平行线的判定求出即可.
【解答】解:∵CD⊥AB,EF⊥AB,
∴∠CMB=∠ENB=90°,
∴CD∥EF.
故答案为:平行.
【点评】本题主要考查对垂线,平行线的判定等知识点的理解和掌握,能求出∠CMB=∠ENB=90°是解此题的关键.21*cnjy*com
7. 162° .
【分析】直接利用垂直的定义结合,∠BOC与∠BOA的度数之比得出答案.
【解答】解:∵BO⊥AO,∠BOC与∠BOA的度数之比为1:5,
∴∠COA=×90°=72°,
则∠BOC=18°,
故∠BOC的补角=180°﹣18°=162°.
故答案为:72°,162°.
【点评】此题主要考查了垂直的定义以及互补的定义,正确得出∠COA的度数是解题关键.
8. 110 °.
【分析】先根据垂直的定义求出∠BOE=90°,然后求出∠BOD的度数,再根据对顶角相等求出∠AOC的度数,再根据邻补角的定义求出∠COB的度数.【21cnj*y.co*m】
【解答】解:∵OE⊥AB,
∴∠BOE=90°,
∵∠EOD=20°,
∴∠BOD=∠BOE﹣∠EOD=90°﹣20°=70°,
∴∠COB=180°﹣∠BOD=180°﹣70°=110°.
故答案为:110.
【点评】本题考查了垂线的定义,对顶角相等,邻补角的和等于180°,要注意领会由垂直得直角这一要点.
9. ①②③ .
【分析】根据垂线、角之间的和与差,即可解答.
【解答】解:∵OE⊥CD于O,∠EOF=α,
∴∠DOF=α﹣90°,
∵OD平分∠BOF,
∴∠BOD=∠FOD,
∵∠AOC=∠BOD,
∴∠AOC=∠FOD,
∴∠AOC=α﹣90°,①正确;
∴∠BOE=180°﹣∠COE﹣∠AOC=180°﹣90°﹣(α﹣90°)=180°﹣α,②正确;
∴∠AOF=180°﹣∠AOC﹣∠DOF=180°﹣(α﹣90°)﹣(α﹣90°)=360°﹣2α,③正确;
故答案为:①②③
【点评】本题考查了垂线,解决本题的关键是利用角之间的关系解答.
三.综合题
10.【分析】直接利用角平分线的定义得出∠EOC=34°,再利用对顶角的定义得出∠BOD的度数,进而得出答案.www-2-1-cnjy-com
【解答】解:∵OF平分∠COE,
∴∠EOF=∠FOC=17°,
∴∠EOC=34°,
∴∠BOD=34°,
∵OA⊥BC,
∴∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+34°=124°.
【点评】此题主要考查了垂线的定义以及角平分线的定义,正确得出∠BOD的度数是解题关键.
11.【分析】(1)根据垂直定义可得∠AOM=90°,进而可得∠1+∠AOC=90°,再利用等量代换可得到∠2+∠AOC=90°,从而可得ON⊥CD;【21教育名师】
(2)根据垂直定义和条件可得∠1=30°,∠BOC=120°,再根据邻补角定义可得∠MOD的度数.
【解答】解:(1)ON⊥CD.
理由如下:
∵OM⊥AB,
∴∠AOM=90°,
∴∠1+∠AOC=90°,
又∵∠1=∠2,
∴∠2+∠AOC=90°,
即∠CON=90°,
∴ON⊥CD.
(2)∵OM⊥AB,∠BOC=4∠1,
∴∠1=30°,∠BOC=120°,
又∵∠1+∠MOD=180°,
∴∠MOD=180°﹣∠1=150°.
【点评】此题主要垂直定义,关键是掌握垂线的定义当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
