数学五年级下人教版9《总复习》统 计 课件(30张)
文档属性
| 名称 | 数学五年级下人教版9《总复习》统 计 课件(30张) |  | |
| 格式 | zip | ||
| 文件大小 | 291.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-31 08:33:27 | ||
图片预览










文档简介
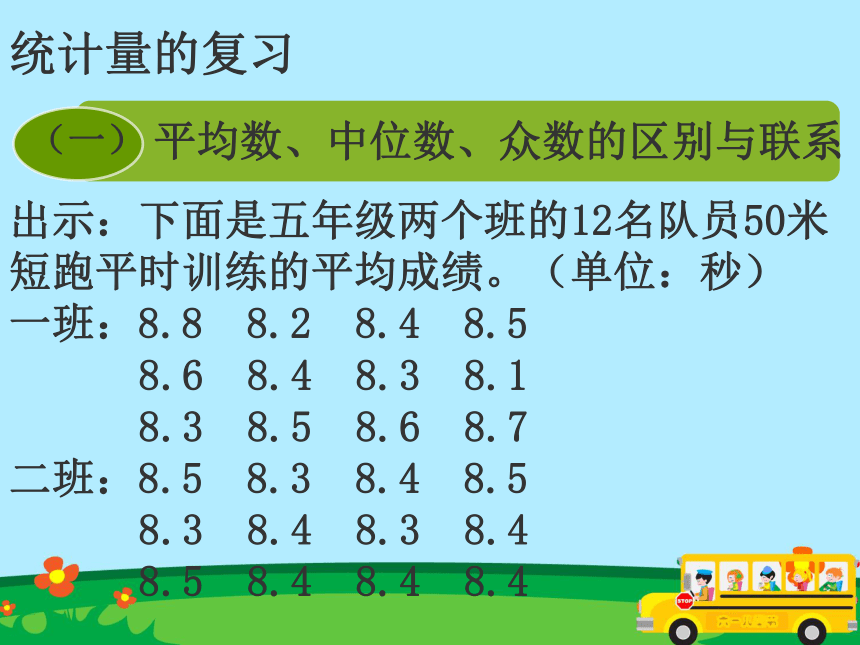
课件30张PPT。统 计第六单元本单元知识点:统计量的复习出示:下面是五年级两个班的12名队员50米短跑平时训练的平均成绩。(单位:秒)
一班:8.8 8.2 8.4 8.5
8.6 8.4 8.3 8.1
8.3 8.5 8.6 8.7
二班:8.5 8.3 8.4 8.5
8.3 8.4 8.3 8.4
8.5 8.4 8.4 8.4 (1)这两组数据的平均数、中位数和众数各是多少?(2)你认为分别用哪个数据代表一班和
二班的成绩比较合适?(3)如果这两个班进行50米往返接力比赛,你认为哪个班获胜的可能性大?
为什么? 平均数=数据之和÷个数
一组数据的平均数只有一个(1)这两组数据的平均数、中位数和众数各是多少?中位数:
奇数个数据,按大小排序最中间的
一个数据;
偶数个数据,按大小排序最中间的
两个数据的平均数。
一组数据的中位数只有一个 (1)这两组数据的平均数、中位数和众数各是多少? 众数:出现次数最多的数据。
一组数据的众数可能有1个或多个(也可能没有) (1)这两组数据的平均数、中位数和众数各是多少?(2)你认为分别用哪个数据代表一班和
二班的成绩比较合适?相同点:
1.都是来描述数据集中趋势的统计量;
2.都可用来反映数据的一般水平;
3.都可用来作为一组数据的代表。不同点:
(1)平均数是“虚拟数”,
中位数不完全是“虚拟数”;
众数是一组数据中的原数据 ,
它是真实存在的。 不同点:(2)平均数的大小与一组数据里的每个数
据都有关系。
中位数则仅与一组数据的排列位置有
关。
众数的大小只与这组数据中的部分数
据有关,不受极端值的影响。
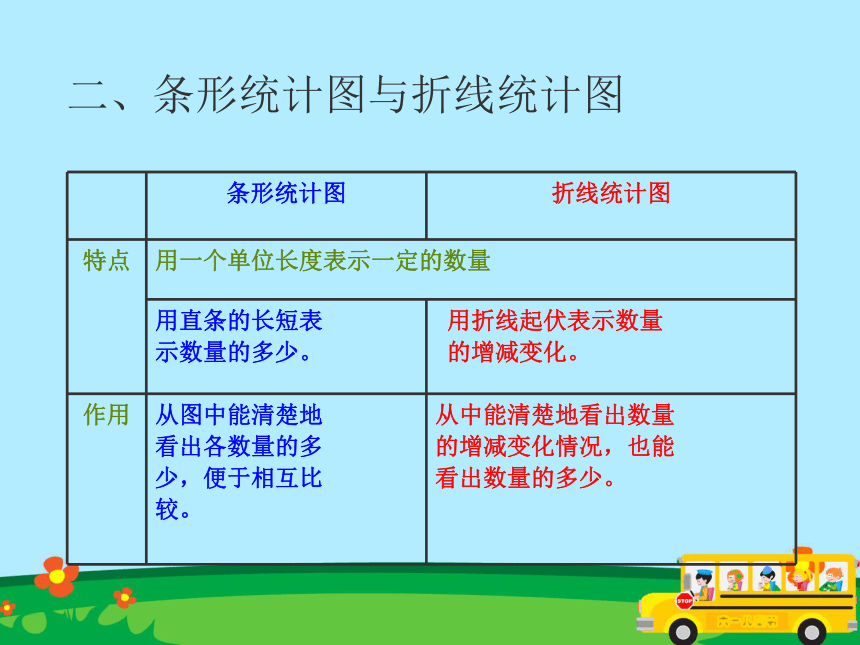
二、条形统计图与折线统计图1.计算错误易错的地方第一小组有5名学生,数学第六单元测验成绩分别是:93、96、88、76、99,求这一小组的平均分? 2.求中位数没有把数据排序 如:有6人比赛立定跳远,成绩如下:
2.25米、1.66米、1.86米、
1.78米、1.69米、1.74米
这组数据的中位数是( ) 易错的地方 3.不能正确选取代表一组数据一
般水平的数值。
易错的地方易错的地方:
不能正确确定基本事件(总可能事件)。 根据下面三组数据,在平均数、中位数、众数这三个统计量中选用哪个统计量能更好地反映各组数据的一般水平?
表一:五(1)班第一小组同学一分钟内口算成绩统计表表二:五(1)班第一小组同学语文考试成绩统计表表三:五(1)班第一小组同学一分钟内投篮成绩统计表操作方法:
1. 让学生先分别计算出每张表中数据的
平均数。 2. 提问:选用哪个统计量能更好地反映各
组数的一般水平?
(97+96+95+94+90+88+28)÷7=84(分)表一:五(1)班第一小组同学一分钟内口算成绩统计表28应该采用中位数“94”来反映这组同学的
口算成绩的一般水平比较合理表二:五(1)班第一小组同学语文考试成绩统计表没有极端数据,所以采用平均数是可以的。表三:五(1)班第一小组同学一分钟内投篮成绩统计表例如:关于甲、乙两地月平均气温的
情况用复式折线统计图表示。
复式折线统计图的特点:
便于比较两种数据的变化趋势和差异性。例如:关于国庆60周年与50周年
阅兵式方阵数量统计图。
复式条形统计图的特点:
便于比较不同组之间的同类数据。1.选择
(1)心脏科要把病人的血压变化情况绘制成统计图,最佳选择是( )
A 条形统计图 B折线统计图
(2)要表示某校各班向灾区捐款情况,选用( )比较合适。
A 条形统计图 B折线统计图概率部分的复习2010年北京市对五年级数学质量监控的框架中对可能性的要求是:
(1)初步体验有些事件的发生是确定的,有些则是不确定的。可能性是有大小的。
(2)能够列出简单试验所有可能发生的结果。
(3)知道事件发生的可能。1.用分数表示事件发生可能性的大小
(1)明确事件可能发生的所有情况(列表或排列组合)
(2)用所有可能出现情况的数量作分母,某一种情况出现的数量作分子。
2.会判断游戏规则的公平性
看每种情况出现的可能性是否相等。
相等,则游戏规则公平。
不相等,则游戏规则不公平。 达到:
(1)会求一些简单事件发生的可能性。
(2)能设计一个方案,符合指定的要求。
(3)对简单事件发生的可能性做出预
测,并阐述自己的理由。1.判断
(1)我扔硬币4次,正面朝上的一定有2次。()
(2)浙江的夏天温度可能超过30摄氏度。()
(3)明天我遇到的第一个人一定是同学。()
(4)不遵守交通规则,发生事故的可能性很大。
()2.填空
盒子里有4个大小和形状都一样的球,
分别是1个白球、1个红球、1个黄球和1
个黑球 。
(1)从中任意摸出两个球,有( )种
可能。
(2)摸出1红1黄的可能性是( )。3.设计转盘
利用下边的空白转盘设计一个实验,转盘上设计红色、黄色、绿色三块区域,使指针停在红色区域的可能性分别是停在绿色区域和黄色区域的2倍。
一班:8.8 8.2 8.4 8.5
8.6 8.4 8.3 8.1
8.3 8.5 8.6 8.7
二班:8.5 8.3 8.4 8.5
8.3 8.4 8.3 8.4
8.5 8.4 8.4 8.4 (1)这两组数据的平均数、中位数和众数各是多少?(2)你认为分别用哪个数据代表一班和
二班的成绩比较合适?(3)如果这两个班进行50米往返接力比赛,你认为哪个班获胜的可能性大?
为什么? 平均数=数据之和÷个数
一组数据的平均数只有一个(1)这两组数据的平均数、中位数和众数各是多少?中位数:
奇数个数据,按大小排序最中间的
一个数据;
偶数个数据,按大小排序最中间的
两个数据的平均数。
一组数据的中位数只有一个 (1)这两组数据的平均数、中位数和众数各是多少? 众数:出现次数最多的数据。
一组数据的众数可能有1个或多个(也可能没有) (1)这两组数据的平均数、中位数和众数各是多少?(2)你认为分别用哪个数据代表一班和
二班的成绩比较合适?相同点:
1.都是来描述数据集中趋势的统计量;
2.都可用来反映数据的一般水平;
3.都可用来作为一组数据的代表。不同点:
(1)平均数是“虚拟数”,
中位数不完全是“虚拟数”;
众数是一组数据中的原数据 ,
它是真实存在的。 不同点:(2)平均数的大小与一组数据里的每个数
据都有关系。
中位数则仅与一组数据的排列位置有
关。
众数的大小只与这组数据中的部分数
据有关,不受极端值的影响。
二、条形统计图与折线统计图1.计算错误易错的地方第一小组有5名学生,数学第六单元测验成绩分别是:93、96、88、76、99,求这一小组的平均分? 2.求中位数没有把数据排序 如:有6人比赛立定跳远,成绩如下:
2.25米、1.66米、1.86米、
1.78米、1.69米、1.74米
这组数据的中位数是( ) 易错的地方 3.不能正确选取代表一组数据一
般水平的数值。
易错的地方易错的地方:
不能正确确定基本事件(总可能事件)。 根据下面三组数据,在平均数、中位数、众数这三个统计量中选用哪个统计量能更好地反映各组数据的一般水平?
表一:五(1)班第一小组同学一分钟内口算成绩统计表表二:五(1)班第一小组同学语文考试成绩统计表表三:五(1)班第一小组同学一分钟内投篮成绩统计表操作方法:
1. 让学生先分别计算出每张表中数据的
平均数。 2. 提问:选用哪个统计量能更好地反映各
组数的一般水平?
(97+96+95+94+90+88+28)÷7=84(分)表一:五(1)班第一小组同学一分钟内口算成绩统计表28应该采用中位数“94”来反映这组同学的
口算成绩的一般水平比较合理表二:五(1)班第一小组同学语文考试成绩统计表没有极端数据,所以采用平均数是可以的。表三:五(1)班第一小组同学一分钟内投篮成绩统计表例如:关于甲、乙两地月平均气温的
情况用复式折线统计图表示。
复式折线统计图的特点:
便于比较两种数据的变化趋势和差异性。例如:关于国庆60周年与50周年
阅兵式方阵数量统计图。
复式条形统计图的特点:
便于比较不同组之间的同类数据。1.选择
(1)心脏科要把病人的血压变化情况绘制成统计图,最佳选择是( )
A 条形统计图 B折线统计图
(2)要表示某校各班向灾区捐款情况,选用( )比较合适。
A 条形统计图 B折线统计图概率部分的复习2010年北京市对五年级数学质量监控的框架中对可能性的要求是:
(1)初步体验有些事件的发生是确定的,有些则是不确定的。可能性是有大小的。
(2)能够列出简单试验所有可能发生的结果。
(3)知道事件发生的可能。1.用分数表示事件发生可能性的大小
(1)明确事件可能发生的所有情况(列表或排列组合)
(2)用所有可能出现情况的数量作分母,某一种情况出现的数量作分子。
2.会判断游戏规则的公平性
看每种情况出现的可能性是否相等。
相等,则游戏规则公平。
不相等,则游戏规则不公平。 达到:
(1)会求一些简单事件发生的可能性。
(2)能设计一个方案,符合指定的要求。
(3)对简单事件发生的可能性做出预
测,并阐述自己的理由。1.判断
(1)我扔硬币4次,正面朝上的一定有2次。()
(2)浙江的夏天温度可能超过30摄氏度。()
(3)明天我遇到的第一个人一定是同学。()
(4)不遵守交通规则,发生事故的可能性很大。
()2.填空
盒子里有4个大小和形状都一样的球,
分别是1个白球、1个红球、1个黄球和1
个黑球 。
(1)从中任意摸出两个球,有( )种
可能。
(2)摸出1红1黄的可能性是( )。3.设计转盘
利用下边的空白转盘设计一个实验,转盘上设计红色、黄色、绿色三块区域,使指针停在红色区域的可能性分别是停在绿色区域和黄色区域的2倍。
