17.1 与三角形有关的线段 课件(第1课时)
文档属性
| 名称 | 17.1 与三角形有关的线段 课件(第1课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-01 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
17.1 与三角形有关的线段
第1课时 三角形的边
生活常识
生活常识
生活常识
在我们的生活中几乎随处可见三角形。它简单,有趣,也十分有用。三角形可以帮助我们更好认识周围世界,解决很多的实际问题。那什么样的图形是三角形呢?
想一想
由不在同一条直线上的三条线段
首尾顺次相接组成的图形,称为三角形.
不在同一条直线上
首尾顺次相接
一、三角形的定义
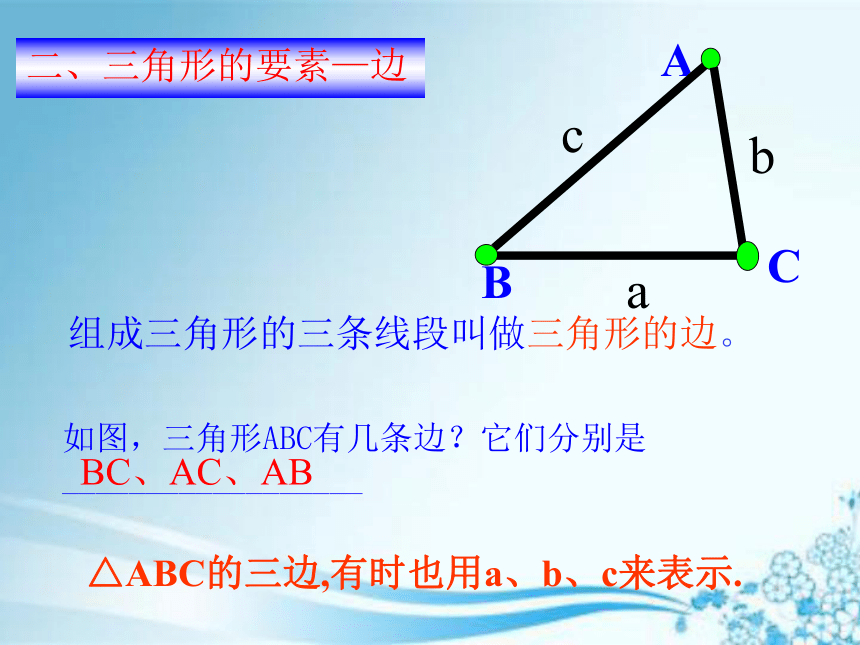
组成三角形的三条线段叫做三角形的边。
如图,三角形ABC有几条边?它们分别是__________________
A
B
C
△ABC的三边,有时也用a、b、c来表示.
a
b
c
二、三角形的要素—边
BC、AC、AB
三角形相邻两边的公共端点叫做三角形的顶点。
如图,三角形ABC有几个顶点?
它们分别是_________________
A
B
C
三角形的形状、大小和位置由它的三个顶点确定。
三、三角形的要素—顶点
点A、B、C
B
C
A
三角形相邻两边所组成的角叫做三角形的内角。简称三角形的角。
如图,三角形ABC有几个内角?它们分是什么
四、三角形的要素—内角
∠A、∠B、∠C
B
C
A
在 ABC中,AB边所对的角是:
∠A所对的边是:
∠C
BC
再说几个对边与对角的关系试试。
五、三角形的对边与对角
A
B
C
记法:
我的姓是“△”
我的名字是:
三个顶点字母“ABC”
注意:表示三角形时,字母没有先后顺序,但通常按逆时针来排列.
六、三角形的表示法
△ABC (或△BCA△CBA 等)
A
D
B
E
C
1.图中共有 个三角形,它们分别是 :__________________________
5
△ABE, △ABC,△BCE, △BCD ,△CDE
小结:数三角形的个数时,抓住不在同一条直线上的三个点能组成一个三角形;再按字母的顺序去数.
练习一
两点之间的所有连线中,线段最短
在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
谈谈你的想法!
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
AB - CB <AC
AC - AB <CB
CB - AC <AB
三角形任何两边之和大于第三边
两点之间的所有连线中,线段最短
七、三角形三边的关系
A
B
C
a
c
b
三角形三边的关系
三角形任意两边
的和大于第三边
三角形任意两边
的差小于第三边
a-bb-cc-ab+c>a
a+c>b
a+b>c
下列长度的各组线段能否组成一个三角形?为什么?
(1)3、4、8 (2)5、6、11
(3)5、6、10
(2) 因为5+6=11,所以这三条线段不能组成一个三角形.
(3) 因为5+6>10,所以这三条线段能组成一个三角形.
(1) 因为3+4<8,所以这三条线段不能组成一个三角形.
解:
练习二
较小两边之和大于第三边,才能构成三角形
结论:
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
构成三角形的条件
张老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,第三根的长度X的取值范围是多少?
10㎝<x<28㎝
练习三
如果告诉你:三角形两边的长度,
第三边长度的范围你能确定吗?
已知三角形两边的长度,第三边长度范围是:
大于这两边的差,小于这两边的和。
人行横道
你能用数学知识解释吗
为什么经常有些行人斜穿马路而不走人行横道
或两点之间的所有连线中,线段最短
三角形任意两边之和大于第三边。
A
B
理由:
C
.
学以致用
用 一条长为18cm的细绳围成一个等腰三角形。
(1)如果腰长是底边长的2倍,那么各边 的长是多少?
分析:等腰三角形有什么特点
提示:设底边长为x cm,则腰长为2x cm
例题:
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
分析:长为4cm的边可能是腰,也可能是底边,所以要分情况来讨论。
情况一:底边长为4cm,设腰长为x cm
情况二:腰长为4cm,设底边长为x cm
注:最后还要判断这三边长能否构成三角形
三角形的基本要素:
边
基本要素
角
顶点
A
B
C
(AB、BC、CA)
(∠A、∠B、∠C)
(A、B、C)
如上面的三角形ABC记作:
三角形的表示:
(用符号“△”表示)
△ABC
b
c
a
三角形:由不在同一直线上的三条线段首尾顺次相接 所组成的图形.
小结
1、三角形的三边关系的性质:
(1)判断三条已知线段能否组成三角形时,采用一种较为简便的判法:若最短边与较长边的和大于最长边,则可构成三角形,否则不能.
2、
(2)确定三角形第三边的取值范围:
三角形的任何两边的和大于第三边。
小结
两边之差<第三边<两边之和
作业及要求
必做:P51 练习 第1、2题
选做:P55 习题 第1、2题
作业要求:
1.抄题目,画图要用铅笔和尺子
2.字体要工整、干净
17.1 与三角形有关的线段
第1课时 三角形的边
生活常识
生活常识
生活常识
在我们的生活中几乎随处可见三角形。它简单,有趣,也十分有用。三角形可以帮助我们更好认识周围世界,解决很多的实际问题。那什么样的图形是三角形呢?
想一想
由不在同一条直线上的三条线段
首尾顺次相接组成的图形,称为三角形.
不在同一条直线上
首尾顺次相接
一、三角形的定义
组成三角形的三条线段叫做三角形的边。
如图,三角形ABC有几条边?它们分别是__________________
A
B
C
△ABC的三边,有时也用a、b、c来表示.
a
b
c
二、三角形的要素—边
BC、AC、AB
三角形相邻两边的公共端点叫做三角形的顶点。
如图,三角形ABC有几个顶点?
它们分别是_________________
A
B
C
三角形的形状、大小和位置由它的三个顶点确定。
三、三角形的要素—顶点
点A、B、C
B
C
A
三角形相邻两边所组成的角叫做三角形的内角。简称三角形的角。
如图,三角形ABC有几个内角?它们分是什么
四、三角形的要素—内角
∠A、∠B、∠C
B
C
A
在 ABC中,AB边所对的角是:
∠A所对的边是:
∠C
BC
再说几个对边与对角的关系试试。
五、三角形的对边与对角
A
B
C
记法:
我的姓是“△”
我的名字是:
三个顶点字母“ABC”
注意:表示三角形时,字母没有先后顺序,但通常按逆时针来排列.
六、三角形的表示法
△ABC (或△BCA△CBA 等)
A
D
B
E
C
1.图中共有 个三角形,它们分别是 :__________________________
5
△ABE, △ABC,△BCE, △BCD ,△CDE
小结:数三角形的个数时,抓住不在同一条直线上的三个点能组成一个三角形;再按字母的顺序去数.
练习一
两点之间的所有连线中,线段最短
在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
谈谈你的想法!
●
●
●
A
B
C
AC + CB >AB
CB + AB >AC
AB + AC >CB
AB - CB <AC
AC - AB <CB
CB - AC <AB
三角形任何两边之和大于第三边
两点之间的所有连线中,线段最短
七、三角形三边的关系
A
B
C
a
c
b
三角形三边的关系
三角形任意两边
的和大于第三边
三角形任意两边
的差小于第三边
a-b
a+c>b
a+b>c
下列长度的各组线段能否组成一个三角形?为什么?
(1)3、4、8 (2)5、6、11
(3)5、6、10
(2) 因为5+6=11,所以这三条线段不能组成一个三角形.
(3) 因为5+6>10,所以这三条线段能组成一个三角形.
(1) 因为3+4<8,所以这三条线段不能组成一个三角形.
解:
练习二
较小两边之和大于第三边,才能构成三角形
结论:
只要满足较小的两条线段之和大于第三条线段,便可构成三角形;若不满足,则不能构成三角形.
构成三角形的条件
张老师想制作一个三角形木架,现有两根长度为19cm和9cm的木棒,第三根的长度X的取值范围是多少?
10㎝<x<28㎝
练习三
如果告诉你:三角形两边的长度,
第三边长度的范围你能确定吗?
已知三角形两边的长度,第三边长度范围是:
大于这两边的差,小于这两边的和。
人行横道
你能用数学知识解释吗
为什么经常有些行人斜穿马路而不走人行横道
或两点之间的所有连线中,线段最短
三角形任意两边之和大于第三边。
A
B
理由:
C
.
学以致用
用 一条长为18cm的细绳围成一个等腰三角形。
(1)如果腰长是底边长的2倍,那么各边 的长是多少?
分析:等腰三角形有什么特点
提示:设底边长为x cm,则腰长为2x cm
例题:
(2)能围成有一边的长是4cm的等腰三角形吗?为什么?
分析:长为4cm的边可能是腰,也可能是底边,所以要分情况来讨论。
情况一:底边长为4cm,设腰长为x cm
情况二:腰长为4cm,设底边长为x cm
注:最后还要判断这三边长能否构成三角形
三角形的基本要素:
边
基本要素
角
顶点
A
B
C
(AB、BC、CA)
(∠A、∠B、∠C)
(A、B、C)
如上面的三角形ABC记作:
三角形的表示:
(用符号“△”表示)
△ABC
b
c
a
三角形:由不在同一直线上的三条线段首尾顺次相接 所组成的图形.
小结
1、三角形的三边关系的性质:
(1)判断三条已知线段能否组成三角形时,采用一种较为简便的判法:若最短边与较长边的和大于最长边,则可构成三角形,否则不能.
2、
(2)确定三角形第三边的取值范围:
三角形的任何两边的和大于第三边。
小结
两边之差<第三边<两边之和
作业及要求
必做:P51 练习 第1、2题
选做:P55 习题 第1、2题
作业要求:
1.抄题目,画图要用铅笔和尺子
2.字体要工整、干净
