人教版小学五年级数学上 5 实际问题与方程(一)课件 (共19张PPT)
文档属性
| 名称 | 人教版小学五年级数学上 5 实际问题与方程(一)课件 (共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 951.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-02 00:00:00 | ||
图片预览






文档简介
课件19张PPT。第五单元 简易方程第5课时
实际问题与方程(一) 1.能根据题中的数量关系正确列出方程并解答。
2.进一步掌握列方程解应用题的步骤,学会寻找已知条件和所求问题之间的相等关系。知识要点:列方程解应用题的一般方法。
(1)理解题意,设未知数为x;
(2)找出等量关系列方程;
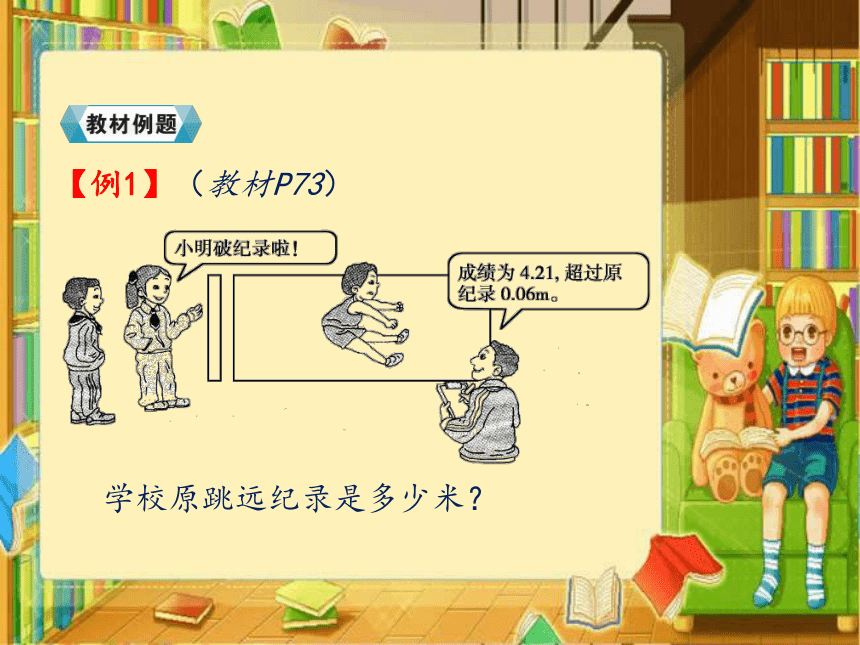
(3)解方程并检验作答。【例1】(教材P73) 学校原跳远纪录是多少米?【解题点拨】方法一:根据题意可知,学校原跳远记录=小明的成绩-超出纪录的部分,由此可计算出其结果。
方法二:由于原记录是未知数,可以把它设为xm,再根据“原记录+超出部分=小明的成绩”列方程解答。【规范解答】方法一:算术方法。
4.21-0.06=4.15(m)
方法二:列方程法。
设学校原跳远纪录是xm。
x+0.06=4.21
x+0.06-0.06=4.21-0.06
x=4.15
答:学校原跳远记录是4.15m。☆动脑练一练1
一个数的3倍与31的和是43,求这个数。【例2】(教材P74)【解题点拨】通过对题目的分析,知其白色皮的块数与黑色皮的块数之间的关系可用下面的线段图来表示: 依题意,黑色皮的块数与白色皮的块数有如下的关系:【解题点拨】
黑色皮的块数×2-白色皮的块数=4
黑色皮的块数×2-4=白色皮的块数
黑色皮的块数×2=白色皮的块数+4
若设黑色皮的块数为x,则以上三种关系可表示为:
2x-20=4 2x-4=20 2x=20+4
解方程时,要先把2x看作一个整体,求出解后再代入验算。【规范解答】设共有x块黑色皮。
2x-20=4
2x-20+20=4+20←先把2x看成一个整体。
2x=24
2x÷2=24÷2
x=12←黑色皮有12块。
答:共有12块黑色皮。【技巧归纳】(1)把黑色皮、白色皮的块数关系看成一个数的几倍与另一个数比大小的关系,就是求比一个数的几倍多(或少)几的数是多少。
(2)形如ax±b=c的方程,是由ax=y与y±b=c综合而成的。求解时,先把ax看作一个整体,求出ax等于多少,再求x等于多少。☆动脑练一练2
校服厂有250米布,若做160套校服还差70米,则平均每套校服需要用布多少米?【例3】李大妈家有150个鸡蛋,每8个装一盒,装完后还剩6个,这些鸡蛋已装了多少盒?【解题点拨】本题的等量关系是:已装的鸡蛋数+剩下的鸡蛋数=总蛋数。若设已装的盒数为x,则已装的鸡蛋数为8x,数量关系式即可表示成8x+6=150。
别忘了写出用字母x表示未知数的设句哟!【规范解答】设这些鸡蛋已装了x盒。依题意,有
8x+6=150
8x+6-6=150-6
8x=144
8x÷8=144÷8
x=18
答:这些鸡蛋已装了18盒。☆动脑练一练3
2008年北京奥运会中国队一共获得金牌51枚,比2004年雅典奥运会的2倍少13枚。2004年中国队获得多少块金牌?
2.进一步掌握列方程解应用题的步骤,学会寻找已知条件和所求问题之间的相等关系。知识要点:列方程解应用题的一般方法。
(1)理解题意,设未知数为x;
(2)找出等量关系列方程;
(3)解方程并检验作答。【例1】(教材P73) 学校原跳远纪录是多少米?【解题点拨】方法一:根据题意可知,学校原跳远记录=小明的成绩-超出纪录的部分,由此可计算出其结果。
方法二:由于原记录是未知数,可以把它设为xm,再根据“原记录+超出部分=小明的成绩”列方程解答。【规范解答】方法一:算术方法。
4.21-0.06=4.15(m)
方法二:列方程法。
设学校原跳远纪录是xm。
x+0.06=4.21
x+0.06-0.06=4.21-0.06
x=4.15
答:学校原跳远记录是4.15m。☆动脑练一练1
一个数的3倍与31的和是43,求这个数。【例2】(教材P74)【解题点拨】通过对题目的分析,知其白色皮的块数与黑色皮的块数之间的关系可用下面的线段图来表示: 依题意,黑色皮的块数与白色皮的块数有如下的关系:【解题点拨】
黑色皮的块数×2-白色皮的块数=4
黑色皮的块数×2-4=白色皮的块数
黑色皮的块数×2=白色皮的块数+4
若设黑色皮的块数为x,则以上三种关系可表示为:
2x-20=4 2x-4=20 2x=20+4
解方程时,要先把2x看作一个整体,求出解后再代入验算。【规范解答】设共有x块黑色皮。
2x-20=4
2x-20+20=4+20←先把2x看成一个整体。
2x=24
2x÷2=24÷2
x=12←黑色皮有12块。
答:共有12块黑色皮。【技巧归纳】(1)把黑色皮、白色皮的块数关系看成一个数的几倍与另一个数比大小的关系,就是求比一个数的几倍多(或少)几的数是多少。
(2)形如ax±b=c的方程,是由ax=y与y±b=c综合而成的。求解时,先把ax看作一个整体,求出ax等于多少,再求x等于多少。☆动脑练一练2
校服厂有250米布,若做160套校服还差70米,则平均每套校服需要用布多少米?【例3】李大妈家有150个鸡蛋,每8个装一盒,装完后还剩6个,这些鸡蛋已装了多少盒?【解题点拨】本题的等量关系是:已装的鸡蛋数+剩下的鸡蛋数=总蛋数。若设已装的盒数为x,则已装的鸡蛋数为8x,数量关系式即可表示成8x+6=150。
别忘了写出用字母x表示未知数的设句哟!【规范解答】设这些鸡蛋已装了x盒。依题意,有
8x+6=150
8x+6-6=150-6
8x=144
8x÷8=144÷8
x=18
答:这些鸡蛋已装了18盒。☆动脑练一练3
2008年北京奥运会中国队一共获得金牌51枚,比2004年雅典奥运会的2倍少13枚。2004年中国队获得多少块金牌?
