匀变速直线运动位移与时间的关系
文档属性
| 名称 | 匀变速直线运动位移与时间的关系 | 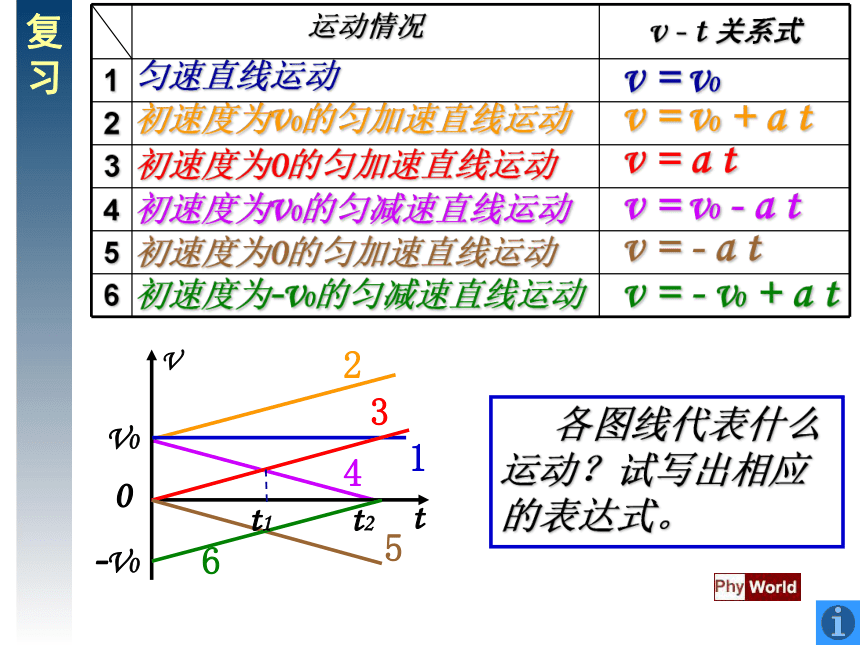 | |
| 格式 | rar | ||
| 文件大小 | 847.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2008-11-29 21:57:00 | ||
图片预览




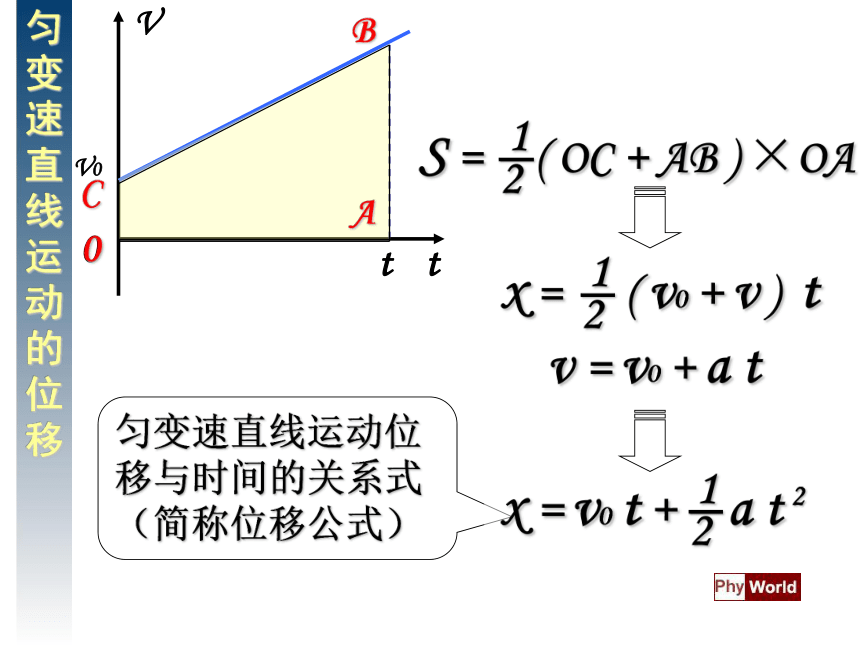

文档简介
课件24张PPT。复习 各图线代表什么运动?试写出相应的表达式。匀速直线运动初速度为v0的匀加速直线运动初速度为0的匀加速直线运动初速度为v0的匀减速直线运动v = v0v = v0 + a tv = a tv = v0 - a t初速度为0的匀加速直线运动初速度为-v0的匀减速直线运动v = - a tv = - v0 + a t第二章 匀变速直线运动的研究3、匀变速直线运动的位移与时间的关系 匀速直线运动的位移x = v t1、规定运动开始时刻为计时起点(即0时刻)
则从运动开始时刻到时刻t ,
时间的变化量为:
2、规定运动的起始时刻物体的位置为坐标原点,
物体在时刻t 的位置坐标为x ,
则在t 时间内的位移:
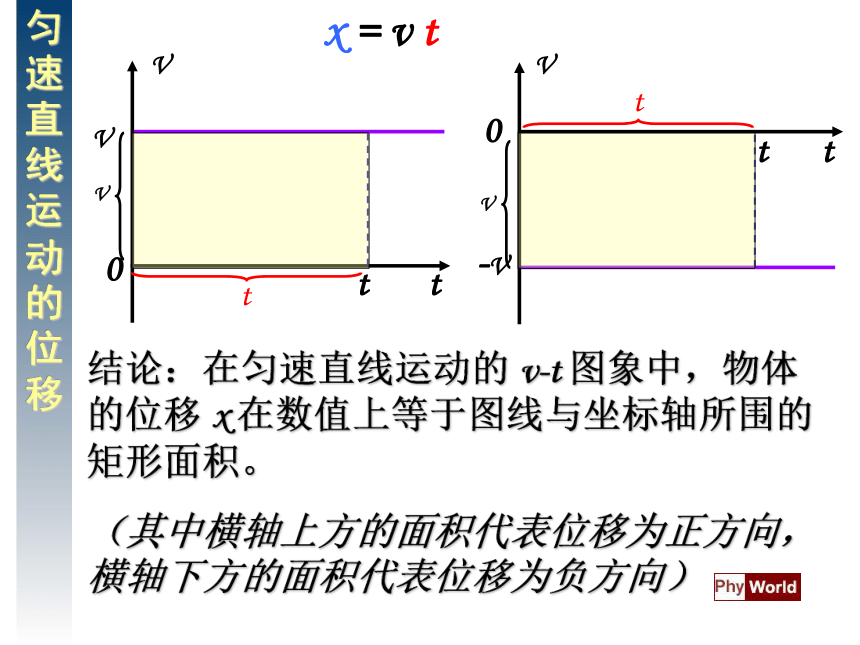
△t = t – 0 = t△x = x – 0 = x匀速直线运动的位移结论:在匀速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的矩形面积。
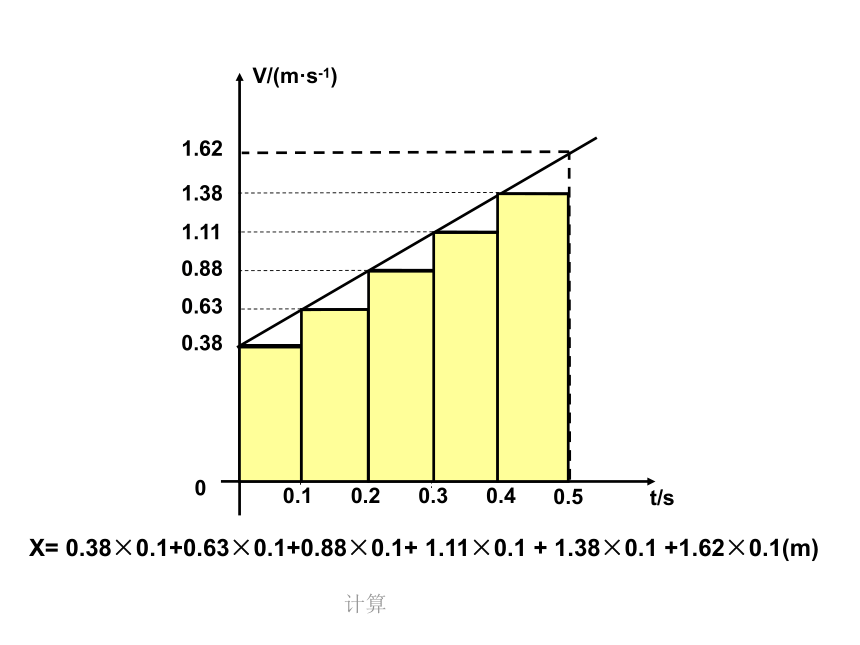
(其中横轴上方的面积代表位移为正方向,横轴下方的面积代表位移为负方向)x = v tV/(m·s-1) 00.50.38 1.62 t/s0.63 0.88 1.11 1.38 0.10.20.30.4计算X= 0.38×0.1+0.63×0.1+0.88×0.1+ 1.11×0.1 + 1.38×0.1 +1.62×0.1(m)匀变速直线运动位移与时间的关系式(简称位移公式)匀变速直线运动的位移ABCv = v0 + a t0匀变速直线运动位移与时间的关系 x-t图像 ——抛物线讨论:(1) 当a= 0时, (2) 当v0= 0时, X= at2X=V0t X/cmt/s 2 134 5 6 7 8 思考:物体作直线运动,为何x-t图象是曲线?X/cmt/s 2 134 5 6 7 8 思考:物体作直线运动,为何x-t图象是曲线?X=V0t + at2讨论:(3)若物体作匀加速运动,则a与 v0 (4)若物体作匀减速运动,则a与 v0------同向------反向at 2V0tX=V0t + at2X=V0t + (-a)t2V0t说明 1.公式 中的 x 、v0 、a 均为矢量,应用时必须选取统一方向为正方向。
2.利用 和
综合应用,可以解决所有的匀变速直线运动。v = v0 + a t应用一:一辆汽车8m/s的初速度作匀加速直线运动行驶了10s,驶过了180m(如图),则汽车运动的加速度是多少?a=把已知数值代入得a= m/s2 =2m/s2汽车行驶的加速度是2m/s2t=10s 应用二: 该同学根据汽车速度计上指针的偏转情况,画出了它的速度时间图象如图中的a,V/(m·s-1)t0t/sova设想在这段时间内另一辆汽车b以相同的初速度作匀变速直线运动,相等的时间内达到相同的末速度,试比较它们在这段时间内位移的大小。v0 内容导航:X=V0t + at2 (1)匀变速直线运动位移与时间的关系:(2) x-t图像 ——抛物线(3) v-t图像中图线与t轴所围的面积对应该时间内物体所发生的位移 已知一物体做直线运动,其位移满足以下公式x=2t+4t2 , x与t的单位分别是m和s,可知物体做___________运动,初速度为____m/s,加速度为_______m/s2。匀加速直线28练习1练习2图示两个物体甲和乙在同一直线上沿同一方向从同以地点同时作匀加速的v-t图线,则在第3s末,它们的位置的关系是( )
A. 甲在乙前6m处
B. 甲在乙前3m处
C. 乙在甲前3m处
D. 乙在甲前6m处B注意刹车问题的陷阱练习3 汽车以l0m/s的速度在平直公路上匀速行驶,刹车后经2s速度为6m/s。求:
(1)刹车过程中的加速度;
(2)刹车后2s内前进的距离;
(3)刹车后前进9m所用的时间;
(4)刹车后8s内前进的距离。练习4 正以30m/s速率前进的列车,接到前方小站的请求:在该站停靠1分钟,接一个垂危病人上车。列车决定先以加速度大小是0.6m/s2匀减速运动到小站恰停止,停车1分钟后再以1.0m/s2的加速度匀加速直线启动,直到恢复原来的速度行驶。求该列车由于临时停车,共耽误多少时间?思考一物体做匀变速直线运动,其相邻相等时间间隔的位移有何特点?v0tt x1 x2思考一物体做匀变速直线运动,其相邻相等时间间隔的位移有何特点?at匀变速直线运动的位移结论:在匀变速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的面积。
(横轴上方的面积与横轴下方的面积有什么分别?)分割、逼近法 分割和逼近的方法在物理学研究中有着广泛的应用。早在公元263年,魏晋时的数学家刘徽首创了“割圆术”——圆内正多边形的边数越多,其周长和面积就越接近圆的周长和面积。割圆术
则从运动开始时刻到时刻t ,
时间的变化量为:
2、规定运动的起始时刻物体的位置为坐标原点,
物体在时刻t 的位置坐标为x ,
则在t 时间内的位移:
△t = t – 0 = t△x = x – 0 = x匀速直线运动的位移结论:在匀速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的矩形面积。
(其中横轴上方的面积代表位移为正方向,横轴下方的面积代表位移为负方向)x = v tV/(m·s-1) 00.50.38 1.62 t/s0.63 0.88 1.11 1.38 0.10.20.30.4计算X= 0.38×0.1+0.63×0.1+0.88×0.1+ 1.11×0.1 + 1.38×0.1 +1.62×0.1(m)匀变速直线运动位移与时间的关系式(简称位移公式)匀变速直线运动的位移ABCv = v0 + a t0匀变速直线运动位移与时间的关系 x-t图像 ——抛物线讨论:(1) 当a= 0时, (2) 当v0= 0时, X= at2X=V0t X/cmt/s 2 134 5 6 7 8 思考:物体作直线运动,为何x-t图象是曲线?X/cmt/s 2 134 5 6 7 8 思考:物体作直线运动,为何x-t图象是曲线?X=V0t + at2讨论:(3)若物体作匀加速运动,则a与 v0 (4)若物体作匀减速运动,则a与 v0------同向------反向at 2V0tX=V0t + at2X=V0t + (-a)t2V0t说明 1.公式 中的 x 、v0 、a 均为矢量,应用时必须选取统一方向为正方向。
2.利用 和
综合应用,可以解决所有的匀变速直线运动。v = v0 + a t应用一:一辆汽车8m/s的初速度作匀加速直线运动行驶了10s,驶过了180m(如图),则汽车运动的加速度是多少?a=把已知数值代入得a= m/s2 =2m/s2汽车行驶的加速度是2m/s2t=10s 应用二: 该同学根据汽车速度计上指针的偏转情况,画出了它的速度时间图象如图中的a,V/(m·s-1)t0t/sova设想在这段时间内另一辆汽车b以相同的初速度作匀变速直线运动,相等的时间内达到相同的末速度,试比较它们在这段时间内位移的大小。v0 内容导航:X=V0t + at2 (1)匀变速直线运动位移与时间的关系:(2) x-t图像 ——抛物线(3) v-t图像中图线与t轴所围的面积对应该时间内物体所发生的位移 已知一物体做直线运动,其位移满足以下公式x=2t+4t2 , x与t的单位分别是m和s,可知物体做___________运动,初速度为____m/s,加速度为_______m/s2。匀加速直线28练习1练习2图示两个物体甲和乙在同一直线上沿同一方向从同以地点同时作匀加速的v-t图线,则在第3s末,它们的位置的关系是( )
A. 甲在乙前6m处
B. 甲在乙前3m处
C. 乙在甲前3m处
D. 乙在甲前6m处B注意刹车问题的陷阱练习3 汽车以l0m/s的速度在平直公路上匀速行驶,刹车后经2s速度为6m/s。求:
(1)刹车过程中的加速度;
(2)刹车后2s内前进的距离;
(3)刹车后前进9m所用的时间;
(4)刹车后8s内前进的距离。练习4 正以30m/s速率前进的列车,接到前方小站的请求:在该站停靠1分钟,接一个垂危病人上车。列车决定先以加速度大小是0.6m/s2匀减速运动到小站恰停止,停车1分钟后再以1.0m/s2的加速度匀加速直线启动,直到恢复原来的速度行驶。求该列车由于临时停车,共耽误多少时间?思考一物体做匀变速直线运动,其相邻相等时间间隔的位移有何特点?v0tt x1 x2思考一物体做匀变速直线运动,其相邻相等时间间隔的位移有何特点?at匀变速直线运动的位移结论:在匀变速直线运动的 v-t 图象中,物体的位移 x 在数值上等于图线与坐标轴所围的面积。
(横轴上方的面积与横轴下方的面积有什么分别?)分割、逼近法 分割和逼近的方法在物理学研究中有着广泛的应用。早在公元263年,魏晋时的数学家刘徽首创了“割圆术”——圆内正多边形的边数越多,其周长和面积就越接近圆的周长和面积。割圆术
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
