人教新版八下19.3课题学习训练卷
图片预览



文档简介
人教新版八下19.3课题学习训练卷
一.选择题(共10小题)(每小题3分,共30分)
1.已知等腰三角形的周长为20cm,底边 ( http: / / www.21cnjy.com )长为y(cm),腰长为x(cm),y与x的函数关系式为y=20﹣2x,那么自变量x的取值范围是( )
A.x>0 B.0<x<10 C.0<x<5 D.5<x<10
2.已知汽车油箱内有油40L,每行驶100 ( http: / / www.21cnjy.com )km耗油10L,则汽车行驶过程中油箱内剩余的油量Q (L)与行驶路程s(km)之间的函数表达式是( )
A.Q=40﹣ ( http: / / www.21cnjy.com ) B.Q=40+ ( http: / / www.21cnjy.com ) C.Q=40﹣ ( http: / / www.21cnjy.com ) D.Q=40+ ( http: / / www.21cnjy.com )
3.平行四边形的周长为50,设它的长为x,宽为y,则y与x的函数关系为( )
A.y=25﹣x B.y=25+x C.y=50﹣x D.y=50+x
4.某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了 ( http: / / www.21cnjy.com ),如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60﹣0.12x,x>0
C.y=0.12x,0≤x≤500 D.y=60﹣0.12x,0≤x≤500
5.一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
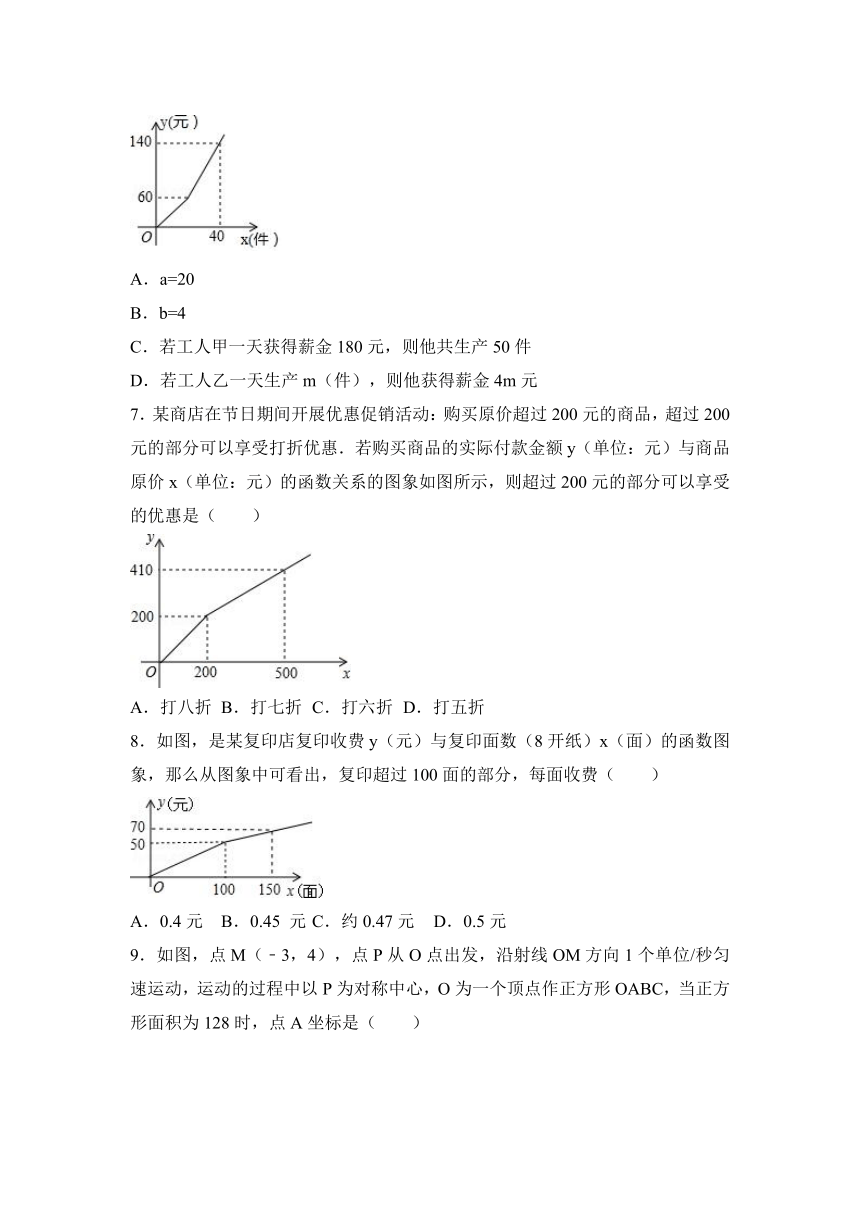
6.某工厂加工一批零件,为了提高工人工作积 ( http: / / www.21cnjy.com )极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
( http: / / www.21cnjy.com )
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产50件
D.若工人乙一天生产m(件),则他获得薪金4m元
7.某商店在节日期间开展优 ( http: / / www.21cnjy.com )惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
( http: / / www.21cnjy.com )
A.打八折 B.打七折 C.打六折 D.打五折
8.如图,是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费( )
( http: / / www.21cnjy.com )
A.0.4元 B.0.45 元 C.约0.47元 D.0.5元
9.如图,点M(﹣3,4),点P从O点 ( http: / / www.21cnjy.com )出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
( http: / / www.21cnjy.com )
A.( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )) B.( ( http: / / www.21cnjy.com ),11) C.(2,2 ( http: / / www.21cnjy.com )) D.( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ))
10.如图,⊙O是以原点为圆心, ( http: / / www.21cnjy.com )为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
( http: / / www.21cnjy.com )
A.3 B.4 C.6﹣ ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )﹣1
二.填空题(共10小题)(每小题3分,共30分)
11.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是Q= .
12.小雨拿5元钱去邮局买面值为80分的邮票,小雨买邮票后所剩钱数y(元)与买邮票的枚数x(枚)之间的关系式为 .
13.平行四边形相邻的两边长为x、y,周长是30,则y与x的函数关系式是 .
14.从A地到B地的距离为60千米 ( http: / / www.21cnjy.com ),一辆摩托车以平均每小时30千米的速度从A地出发到B地,则摩托车距B地的距离s(千米)与行驶时间t(时)的函数表达式为 .
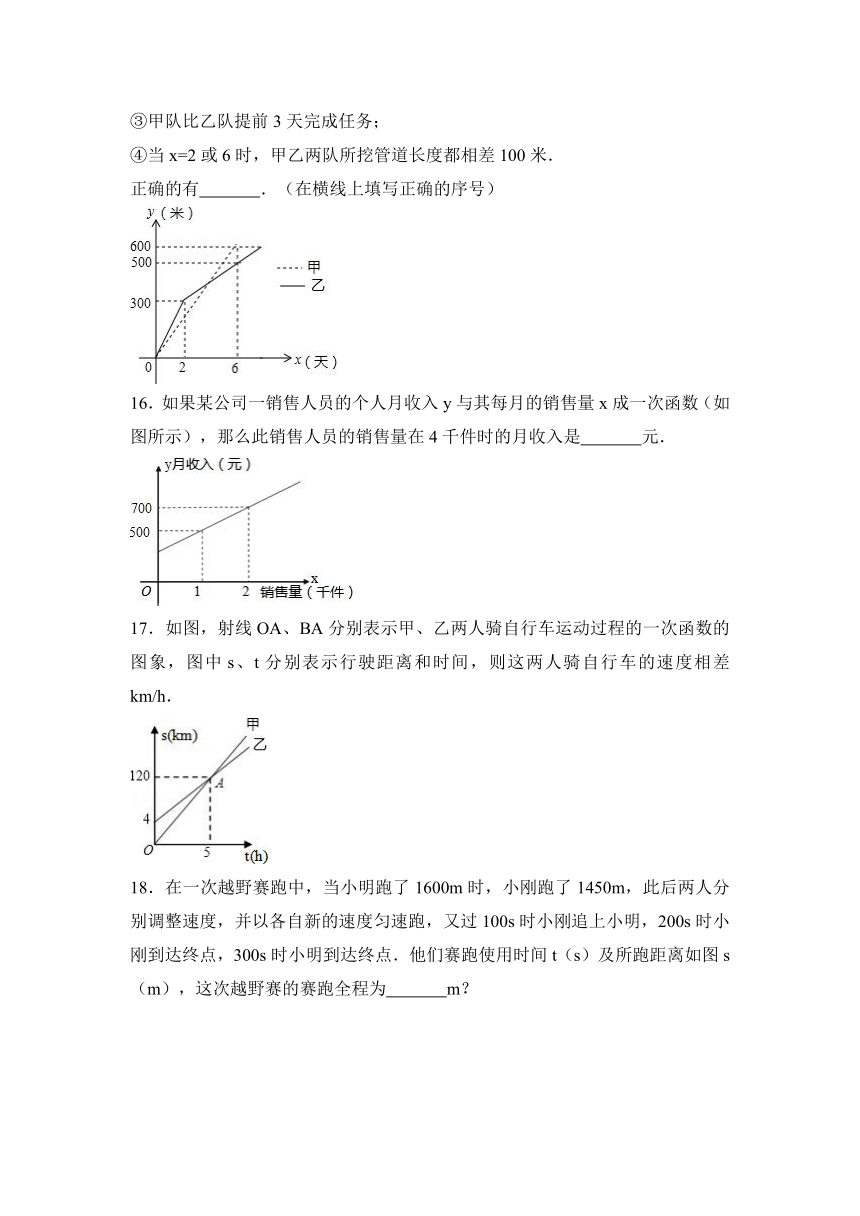
15.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③甲队比乙队提前3天完成任务;
④当x=2或6时,甲乙两队所挖管道长度都相差100米.
正确的有 .(在横线上填写正确的序号)
( http: / / www.21cnjy.com )
16.如果某公司一销售人员的个人月收入y与其每月的销售量x成一次函数(如图所示),那么此销售人员的销售量在4千件时的月收入是 元.
( http: / / www.21cnjy.com )
17.如图,射线OA、BA分别表示 ( http: / / www.21cnjy.com )甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
( http: / / www.21cnjy.com )
18.在一次越野赛跑中,当小明跑了1600m ( http: / / www.21cnjy.com )时,小刚跑了1450m,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.他们赛跑使用时间t(s)及所跑距离如图s(m),这次越野赛的赛跑全程为 m?
( http: / / www.21cnjy.com )
19.如图,矩形ABCD的 ( http: / / www.21cnjy.com )边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点E的坐标为(0,2).点F(x,0)在边AB上运动,若过点E、F的直线将矩形ABCD的周长分成2:1两部分,则x的值为 .
( http: / / www.21cnjy.com )
20.如图,直线 ( http: / / www.21cnjy.com ),点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为 ,点An .
( http: / / www.21cnjy.com )
三.解答题(共8小题)(每小题5分,共40分)
21.已知等腰三角形的周长是20cm,设底边长为y,腰长为x,求y与x的函数关系式,并求出自变量x的取值范围.
22.某汽车客运公司规定 ( http: / / www.21cnjy.com )旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.
(1)求y与x之间的函数关系.
(2)旅客最多可以免费携带多少千克的行李?
( http: / / www.21cnjy.com )
23.已知等腰三角形的周长为24cm,腰长为xcm,底边为ycm,请你用x的式子表示y,并求x的取值范围.
24.某市为鼓励居民节约用水,对每户用 ( http: / / www.21cnjy.com )水按如下标准收费:若每户每月用水不超过8m3,则每m3按1元收费;若每户每月用水超过8m3,则超过部分每m3按2元收费.某用户7月份用水比8m3要多xm3,交纳水费y元.
(1)求y关于x的函数解析式,并写出x的取值范围.
(2)此用户要想每月水费控制在20元以内,那么每月的用水量最多不超过多少m3?
25.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:
x/元 … 15 20 25 …
y/件 … 25 20 15 …
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是多少元?
26.某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌 国内品牌
进价(元/部) 4400 2000
售价(元/部) 5000 2500
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划 ( http: / / www.21cnjy.com )的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
27.如图,直线AB:y=﹣x﹣b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x﹣k(k≠ ( http: / / www.21cnjy.com )0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
( http: / / www.21cnjy.com )
28.如图①,已知直线y=﹣2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
人教新版八下19.3课题学习训练卷答案
一.选择题(共10小题)
1.D.2.C.3.A.4.D.5.D.6.D.7.B.8.A.9.D.10.B.
二.填空题(共10小题)
11.50﹣8x. 12.y=5﹣0.8x. 13.y=﹣x+15(0<x<15).
14.s=60﹣30t(0≤t≤2). 15.①②④. 16.1100. 17. ( http: / / www.21cnjy.com ).
18.2050. 19.± ( http: / / www.21cnjy.com ). 20.( ( http: / / www.21cnjy.com ),0),(( ( http: / / www.21cnjy.com ))n﹣1,0).
三.解答题(共8小题)
21.解:∵2x+y=20,
∴y=20﹣2x,即x<10,
∵两边之和大于第三边,
∴x>5,
综上可得5<x<10.
22.解:(1)设一次函数y=kx+b,
∵当x=60时,y=6,当x=90时,y=10,
∴ ( http: / / www.21cnjy.com ) 解之,得 ( http: / / www.21cnjy.com ),
∴所求函数关系式为y= ( http: / / www.21cnjy.com )x﹣2(x≥15);
(2)当y=0时, ( http: / / www.21cnjy.com )x﹣2=0,所以x=15,
故旅客最多可免费携带15kg行李.
23.解:依题意得2x+y=24,
即y=﹣2x+24;
根据三角形的三边关系得: ( http: / / www.21cnjy.com ),
解得:6<x<12.
24.解:(1)由题意,得
y=2x+8(x>0)
(2)由题意,得
2x+8≤20,
解得:x≤6,
∴x最多=6
∴每月的用水量最多为14m3.
25.解:(1)设日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=kx+b,
( http: / / www.21cnjy.com ),
解得, ( http: / / www.21cnjy.com ),
即日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=﹣x+40;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是:(35﹣10)(﹣35+40)=25×5=125(元),
即当每件产品的销售价定为35元时,此时每日的销售利润是125元.
26.解:(1)设商场计划购进国外品牌手机x部,国内品牌手机y部,由题意,得:
( http: / / www.21cnjy.com ),
解得 ( http: / / www.21cnjy.com ),
答:商场计划购进国外品牌手机20部,国内品牌手机30部;
(2)设国外品牌手机减少a部,则国内手机品牌增加3a部,由题意,得:
0.44(20﹣a)+0.2(30+3a)≤15.6,
解得:a≤5,
设全部销售后获得的毛利润为w万元,由题意,得:
w=0.06(20﹣a)+0.05(30+3a)=0.09a+2.7,
∵k=0.09>0,
∴w随a的增大而增大,
∴当a=5时,w最大=3.15,
答:当该商场购进国外品牌手机15部,国内品牌手机45部时,全部销售后获利最大,最大毛利润为3.15万元.
27.解:(1)将点A(6,0)代入直线AB解析式可得:0=﹣6﹣b,
解得:b=﹣6,
∴直线AB 解析式为y=﹣x+6,
∴B点坐标为:(0,6).
(2)∵OB:OC=3:1,
∴OC=2,
∴点C的坐标为(﹣2,0),
设BC的解析式是y=ax+c,代入得; ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
∴直线BC的解析式是:y=3x+6.
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°.
∵S△EBD=S△FBD,
∴DE=DF.
又∵∠NDF=∠EDM,
∴△NFD≌△EDM,
∴FN=ME,
联立得 ( http: / / www.21cnjy.com ),
解得:yE=﹣ ( http: / / www.21cnjy.com )k+4,
联立 ( http: / / www.21cnjy.com ),
解得:yF=﹣3k﹣12,
∵FN=﹣yF,ME=yE,
∴3k+12=﹣ ( http: / / www.21cnjy.com )k+4,
∴k=﹣2.4;
当k=﹣2.4时,存在直线EF:y=2x+2.4,使得S△EBD=S△FBD.
( http: / / www.21cnjy.com )
28.解:(1)A(2,0);C(0,4)(2分)
(2)由折叠知:CD=AD.设AD=x,则CD=x,BD=4﹣x,
根据题意得:(4﹣x)2+22=x2解得: ( http: / / www.21cnjy.com )
此时,AD= ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )(2分)
设直线CD为y=kx+4,把 ( http: / / www.21cnjy.com )代入得 ( http: / / www.21cnjy.com )(1分)
解得: ( http: / / www.21cnjy.com )
∴直线CD解析式为 ( http: / / www.21cnjy.com )(1分)
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图,
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD= ( http: / / www.21cnjy.com ),PD=BD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),AP=BC=2
由AD×PQ=DP×AP得: ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com ),把 ( http: / / www.21cnjy.com )代入 ( http: / / www.21cnjy.com )得 ( http: / / www.21cnjy.com )
此时 ( http: / / www.21cnjy.com )
(也可通过Rt△APQ勾股定理求AQ长得到点P的纵坐标)
③当点P在第二象限时,如图
同理可求得: ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com )
此时 ( http: / / www.21cnjy.com )
综合得,满足条件的点P有三个,
分别为:P1(0,0); ( http: / / www.21cnjy.com ); ( http: / / www.21cnjy.com ).
(写对第一个(2分),二个(3分),3个且不多写(4分),写对4个且多写得(3分).)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
一.选择题(共10小题)(每小题3分,共30分)
1.已知等腰三角形的周长为20cm,底边 ( http: / / www.21cnjy.com )长为y(cm),腰长为x(cm),y与x的函数关系式为y=20﹣2x,那么自变量x的取值范围是( )
A.x>0 B.0<x<10 C.0<x<5 D.5<x<10
2.已知汽车油箱内有油40L,每行驶100 ( http: / / www.21cnjy.com )km耗油10L,则汽车行驶过程中油箱内剩余的油量Q (L)与行驶路程s(km)之间的函数表达式是( )
A.Q=40﹣ ( http: / / www.21cnjy.com ) B.Q=40+ ( http: / / www.21cnjy.com ) C.Q=40﹣ ( http: / / www.21cnjy.com ) D.Q=40+ ( http: / / www.21cnjy.com )
3.平行四边形的周长为50,设它的长为x,宽为y,则y与x的函数关系为( )
A.y=25﹣x B.y=25+x C.y=50﹣x D.y=50+x
4.某油箱容量为60 L的汽车,加满汽油后行驶了100 km时,油箱中的汽油大约消耗了 ( http: / / www.21cnjy.com ),如果加满汽油后汽车行驶的路程为x km,油箱中剩油量为y L,则y与x之间的函数解析式和自变量取值范围分别是( )
A.y=0.12x,x>0 B.y=60﹣0.12x,x>0
C.y=0.12x,0≤x≤500 D.y=60﹣0.12x,0≤x≤500
5.一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
6.某工厂加工一批零件,为了提高工人工作积 ( http: / / www.21cnjy.com )极性,工厂规定每名工人每次薪金如下:生产的零件不超过a件,则每件3元,超过a件,超过部分每件b元,如图是一名工人一天获得薪金y(元)与其生产的件数x(件)之间的函数关系式,则下列结论错误的是( )
( http: / / www.21cnjy.com )
A.a=20
B.b=4
C.若工人甲一天获得薪金180元,则他共生产50件
D.若工人乙一天生产m(件),则他获得薪金4m元
7.某商店在节日期间开展优 ( http: / / www.21cnjy.com )惠促销活动:购买原价超过200元的商品,超过200元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过200元的部分可以享受的优惠是( )
( http: / / www.21cnjy.com )
A.打八折 B.打七折 C.打六折 D.打五折
8.如图,是某复印店复印收费y(元)与复印面数(8开纸)x(面)的函数图象,那么从图象中可看出,复印超过100面的部分,每面收费( )
( http: / / www.21cnjy.com )
A.0.4元 B.0.45 元 C.约0.47元 D.0.5元
9.如图,点M(﹣3,4),点P从O点 ( http: / / www.21cnjy.com )出发,沿射线OM方向1个单位/秒匀速运动,运动的过程中以P为对称中心,O为一个顶点作正方形OABC,当正方形面积为128时,点A坐标是( )
( http: / / www.21cnjy.com )
A.( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )) B.( ( http: / / www.21cnjy.com ),11) C.(2,2 ( http: / / www.21cnjy.com )) D.( ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ))
10.如图,⊙O是以原点为圆心, ( http: / / www.21cnjy.com )为半径的圆,点P是直线y=﹣x+6上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
( http: / / www.21cnjy.com )
A.3 B.4 C.6﹣ ( http: / / www.21cnjy.com ) D.3 ( http: / / www.21cnjy.com )﹣1
二.填空题(共10小题)(每小题3分,共30分)
11.小军用50元钱去买单价是8元的笔记本,则他剩余的钱Q(元)与他买这种笔记本的本数x之间的关系是Q= .
12.小雨拿5元钱去邮局买面值为80分的邮票,小雨买邮票后所剩钱数y(元)与买邮票的枚数x(枚)之间的关系式为 .
13.平行四边形相邻的两边长为x、y,周长是30,则y与x的函数关系式是 .
14.从A地到B地的距离为60千米 ( http: / / www.21cnjy.com ),一辆摩托车以平均每小时30千米的速度从A地出发到B地,则摩托车距B地的距离s(千米)与行驶时间t(时)的函数表达式为 .
15.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中:
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③甲队比乙队提前3天完成任务;
④当x=2或6时,甲乙两队所挖管道长度都相差100米.
正确的有 .(在横线上填写正确的序号)
( http: / / www.21cnjy.com )
16.如果某公司一销售人员的个人月收入y与其每月的销售量x成一次函数(如图所示),那么此销售人员的销售量在4千件时的月收入是 元.
( http: / / www.21cnjy.com )
17.如图,射线OA、BA分别表示 ( http: / / www.21cnjy.com )甲、乙两人骑自行车运动过程的一次函数的图象,图中s、t分别表示行驶距离和时间,则这两人骑自行车的速度相差 km/h.
( http: / / www.21cnjy.com )
18.在一次越野赛跑中,当小明跑了1600m ( http: / / www.21cnjy.com )时,小刚跑了1450m,此后两人分别调整速度,并以各自新的速度匀速跑,又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.他们赛跑使用时间t(s)及所跑距离如图s(m),这次越野赛的赛跑全程为 m?
( http: / / www.21cnjy.com )
19.如图,矩形ABCD的 ( http: / / www.21cnjy.com )边AB在x轴上,AB的中点与原点O重合,AB=2,AD=1,点E的坐标为(0,2).点F(x,0)在边AB上运动,若过点E、F的直线将矩形ABCD的周长分成2:1两部分,则x的值为 .
( http: / / www.21cnjy.com )
20.如图,直线 ( http: / / www.21cnjy.com ),点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为 ,点An .
( http: / / www.21cnjy.com )
三.解答题(共8小题)(每小题5分,共40分)
21.已知等腰三角形的周长是20cm,设底边长为y,腰长为x,求y与x的函数关系式,并求出自变量x的取值范围.
22.某汽车客运公司规定 ( http: / / www.21cnjy.com )旅客可以随身携带一定重量的行李,如果超过规定的重量,则需要购买行李票,行李票费用y(元)与行李重量x(千克)之间函数关系的图象如图所示.
(1)求y与x之间的函数关系.
(2)旅客最多可以免费携带多少千克的行李?
( http: / / www.21cnjy.com )
23.已知等腰三角形的周长为24cm,腰长为xcm,底边为ycm,请你用x的式子表示y,并求x的取值范围.
24.某市为鼓励居民节约用水,对每户用 ( http: / / www.21cnjy.com )水按如下标准收费:若每户每月用水不超过8m3,则每m3按1元收费;若每户每月用水超过8m3,则超过部分每m3按2元收费.某用户7月份用水比8m3要多xm3,交纳水费y元.
(1)求y关于x的函数解析式,并写出x的取值范围.
(2)此用户要想每月水费控制在20元以内,那么每月的用水量最多不超过多少m3?
25.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如表:
x/元 … 15 20 25 …
y/件 … 25 20 15 …
已知日销售量y是销售价x的一次函数.
(1)求日销售量y(件)与每件产品的销售价x(元)之间的函数表达式;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是多少元?
26.某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌 国内品牌
进价(元/部) 4400 2000
售价(元/部) 5000 2500
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可获毛利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划 ( http: / / www.21cnjy.com )的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润.
27.如图,直线AB:y=﹣x﹣b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
(1)求点B的坐标;
(2)求直线BC的解析式;
(3)直线EF:y=2x﹣k(k≠ ( http: / / www.21cnjy.com )0)交AB于E,交BC于点F,交x轴于点D,是否存在这样的直线EF,使得S△EBD=S△FBD?若存在,求出k的值;若不存在,请说明理由.
( http: / / www.21cnjy.com )
28.如图①,已知直线y=﹣2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.
(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
( http: / / www.21cnjy.com )
人教新版八下19.3课题学习训练卷答案
一.选择题(共10小题)
1.D.2.C.3.A.4.D.5.D.6.D.7.B.8.A.9.D.10.B.
二.填空题(共10小题)
11.50﹣8x. 12.y=5﹣0.8x. 13.y=﹣x+15(0<x<15).
14.s=60﹣30t(0≤t≤2). 15.①②④. 16.1100. 17. ( http: / / www.21cnjy.com ).
18.2050. 19.± ( http: / / www.21cnjy.com ). 20.( ( http: / / www.21cnjy.com ),0),(( ( http: / / www.21cnjy.com ))n﹣1,0).
三.解答题(共8小题)
21.解:∵2x+y=20,
∴y=20﹣2x,即x<10,
∵两边之和大于第三边,
∴x>5,
综上可得5<x<10.
22.解:(1)设一次函数y=kx+b,
∵当x=60时,y=6,当x=90时,y=10,
∴ ( http: / / www.21cnjy.com ) 解之,得 ( http: / / www.21cnjy.com ),
∴所求函数关系式为y= ( http: / / www.21cnjy.com )x﹣2(x≥15);
(2)当y=0时, ( http: / / www.21cnjy.com )x﹣2=0,所以x=15,
故旅客最多可免费携带15kg行李.
23.解:依题意得2x+y=24,
即y=﹣2x+24;
根据三角形的三边关系得: ( http: / / www.21cnjy.com ),
解得:6<x<12.
24.解:(1)由题意,得
y=2x+8(x>0)
(2)由题意,得
2x+8≤20,
解得:x≤6,
∴x最多=6
∴每月的用水量最多为14m3.
25.解:(1)设日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=kx+b,
( http: / / www.21cnjy.com ),
解得, ( http: / / www.21cnjy.com ),
即日销售量y(件)与每件产品的销售价x(元)之间的函数表达式是y=﹣x+40;
(2)当每件产品的销售价定为35元时,此时每日的销售利润是:(35﹣10)(﹣35+40)=25×5=125(元),
即当每件产品的销售价定为35元时,此时每日的销售利润是125元.
26.解:(1)设商场计划购进国外品牌手机x部,国内品牌手机y部,由题意,得:
( http: / / www.21cnjy.com ),
解得 ( http: / / www.21cnjy.com ),
答:商场计划购进国外品牌手机20部,国内品牌手机30部;
(2)设国外品牌手机减少a部,则国内手机品牌增加3a部,由题意,得:
0.44(20﹣a)+0.2(30+3a)≤15.6,
解得:a≤5,
设全部销售后获得的毛利润为w万元,由题意,得:
w=0.06(20﹣a)+0.05(30+3a)=0.09a+2.7,
∵k=0.09>0,
∴w随a的增大而增大,
∴当a=5时,w最大=3.15,
答:当该商场购进国外品牌手机15部,国内品牌手机45部时,全部销售后获利最大,最大毛利润为3.15万元.
27.解:(1)将点A(6,0)代入直线AB解析式可得:0=﹣6﹣b,
解得:b=﹣6,
∴直线AB 解析式为y=﹣x+6,
∴B点坐标为:(0,6).
(2)∵OB:OC=3:1,
∴OC=2,
∴点C的坐标为(﹣2,0),
设BC的解析式是y=ax+c,代入得; ( http: / / www.21cnjy.com ),
解得: ( http: / / www.21cnjy.com ),
∴直线BC的解析式是:y=3x+6.
(3)过E、F分别作EM⊥x轴,FN⊥x轴,则∠EMD=∠FND=90°.
∵S△EBD=S△FBD,
∴DE=DF.
又∵∠NDF=∠EDM,
∴△NFD≌△EDM,
∴FN=ME,
联立得 ( http: / / www.21cnjy.com ),
解得:yE=﹣ ( http: / / www.21cnjy.com )k+4,
联立 ( http: / / www.21cnjy.com ),
解得:yF=﹣3k﹣12,
∵FN=﹣yF,ME=yE,
∴3k+12=﹣ ( http: / / www.21cnjy.com )k+4,
∴k=﹣2.4;
当k=﹣2.4时,存在直线EF:y=2x+2.4,使得S△EBD=S△FBD.
( http: / / www.21cnjy.com )
28.解:(1)A(2,0);C(0,4)(2分)
(2)由折叠知:CD=AD.设AD=x,则CD=x,BD=4﹣x,
根据题意得:(4﹣x)2+22=x2解得: ( http: / / www.21cnjy.com )
此时,AD= ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )(2分)
设直线CD为y=kx+4,把 ( http: / / www.21cnjy.com )代入得 ( http: / / www.21cnjy.com )(1分)
解得: ( http: / / www.21cnjy.com )
∴直线CD解析式为 ( http: / / www.21cnjy.com )(1分)
(3)①当点P与点O重合时,△APC≌△CBA,此时P(0,0)
②当点P在第一象限时,如图,
由△APC≌△CBA得∠ACP=∠CAB,
则点P在直线CD上.过P作PQ⊥AD于点Q,
在Rt△ADP中,
AD= ( http: / / www.21cnjy.com ),PD=BD= ( http: / / www.21cnjy.com )= ( http: / / www.21cnjy.com ),AP=BC=2
由AD×PQ=DP×AP得: ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com ),把 ( http: / / www.21cnjy.com )代入 ( http: / / www.21cnjy.com )得 ( http: / / www.21cnjy.com )
此时 ( http: / / www.21cnjy.com )
(也可通过Rt△APQ勾股定理求AQ长得到点P的纵坐标)
③当点P在第二象限时,如图
同理可求得: ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com )
此时 ( http: / / www.21cnjy.com )
综合得,满足条件的点P有三个,
分别为:P1(0,0); ( http: / / www.21cnjy.com ); ( http: / / www.21cnjy.com ).
(写对第一个(2分),二个(3分),3个且不多写(4分),写对4个且多写得(3分).)
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
