2016-2017学年黑龙江省大庆市杜尔伯特县八年级(下)期末数学试卷(五四学制)(解析版)
文档属性
| 名称 | 2016-2017学年黑龙江省大庆市杜尔伯特县八年级(下)期末数学试卷(五四学制)(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 285.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-04 00:00:00 | ||
图片预览

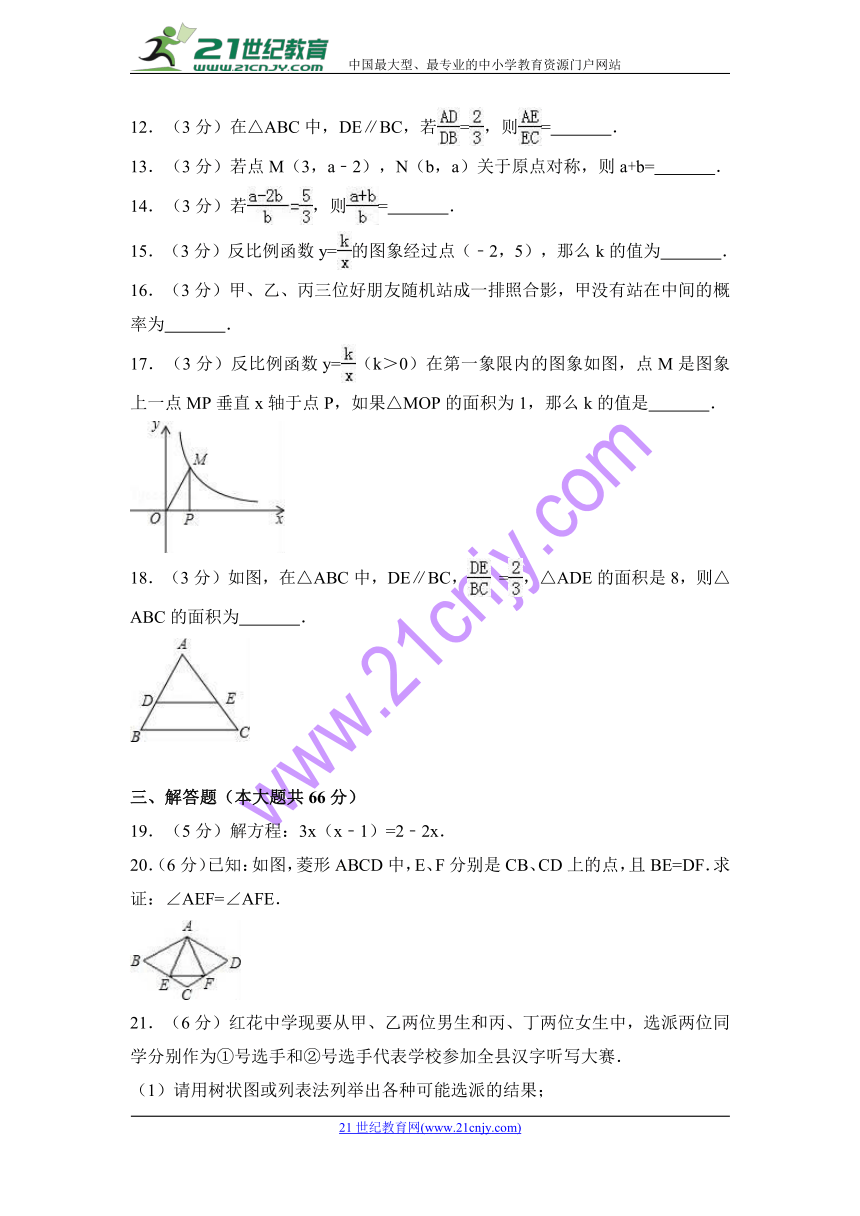


文档简介
2016-2017学年黑龙江省大庆市杜尔伯特县八年级(下)期末数学试卷(五四学制)
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)关于x的一元二次方程3x2=2x﹣1的二次项系数、一次项系数、常数项分别是( )
A.3,﹣2,﹣1 B.3,2,﹣1 C.﹣3,﹣2,1 D.3,﹣2,1
2.(3分)如图是一个水管的三叉接头,它的左视图是( )
A. B. C. D.
3.(3分)从编号为1~10的10个完全相同的球中,任取一球,其号码能被3整除的概率是( )
A. B. C. D.
4.(3分)方程(x﹣2)2=9的解是( )
A.x1=5,x2=﹣1 B.x1=﹣5,x2=1 C.x1=11,x2=﹣7 D.x1=﹣11,x2=7
5.(3分)如图所示,四边形ABCD中,点E、F、G、H分别是其边AB、BC、CD、DA的中点,若四边形EFGH是矩形,则下列说法正确的是( )
A.四边形ABCD是矩形
B.四边形ABCD一定是平行四边形
C.AC⊥BD
D.AC=BD
6.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )
A.正六边形 B.平行四边形 C.正三角形 D.等腰梯形
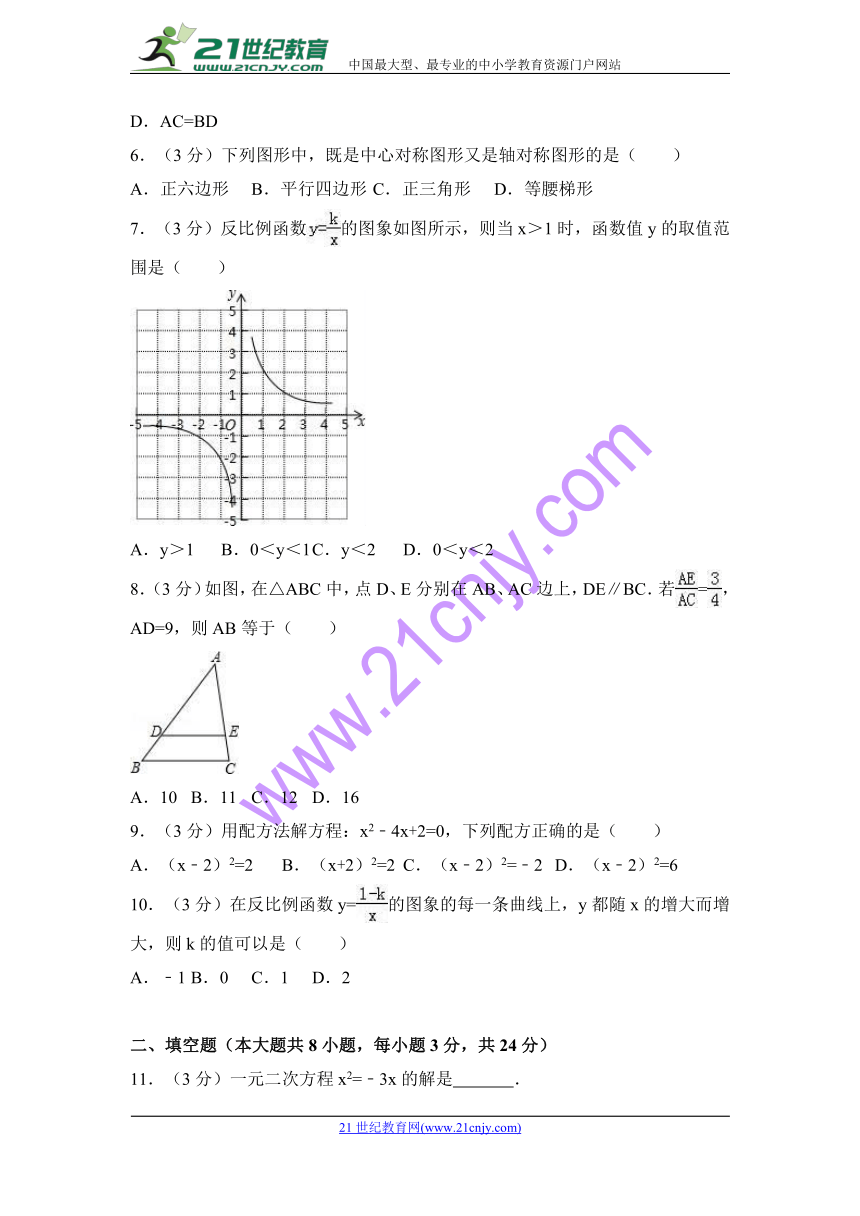
7.(3分)反比例函数的图象如图所示,则当x>1时,函数值y的取值范围是( )
A.y>1 B.0<y<1 C.y<2 D.0<y<2
8.(3分)如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若=,AD=9,则AB等于( )21教育网
A.10 B.11 C.12 D.16
9.(3分)用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )
A.(x﹣2)2=2 B.(x+2)2=2 C.(x﹣2)2=﹣2 D.(x﹣2)2=6
10.(3分)在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
二、填空题(本大题共8小题,每小题3分,共24分)
11.(3分)一元二次方程x2=﹣3x的解是 .
12.(3分)在△ABC中,DE∥BC,若=,则= .
13.(3分)若点M(3,a﹣2),N(b,a)关于原点对称,则a+b= .
14.(3分)若,则= .
15.(3分)反比例函数y=的图象经过点(﹣2,5),那么k的值为 .
16.(3分)甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .
17.(3分)反比例函数y=(k>0)在第一象限内的图象如图,点M是图象上一点MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是 .
18.(3分)如图,在△ABC中,DE∥BC, =,△ADE的面积是8,则△ABC的面积为 .2·1·c·n·j·y
三、解答题(本大题共66分)
19.(5分)解方程:3x(x﹣1)=2﹣2x.
20.(6分)已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.【21教育名师】
21.(6分)红花中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛.
(1)请用树状图或列表法列举出各种可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
22.(6分)如图,△ABC中,∠B=90°,AB=BC,AD是△ABC的角平分线,若BD=1,求DC的长.www.21-cn-jy.com
23.(6分)如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.【21教育】
24.(7分)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
25.(7分)如图,某学校要修建一个矩形ABCD的花圃,花圃的一边AD靠教学楼,其它三边用总长为24米的篱笆围成,设AB边的长为x(单位:米),矩形花圃ABCD的面积为S(单位:平方米).
(1)求S与x之间的函数关系式(不必写出自变量x的取值范围);
(2)当x取多少时,矩形花圃ABCD的面积最大,最大的面积为多少?
26.(7分)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣<0的x的取值范围.
27.(7分)如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
28.(9分)(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.
2016-2017学年黑龙江省大庆市杜尔伯特县八年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)关于x的一元二次方程3x2=2x﹣1的二次项系数、一次项系数、常数项分别是( )
A.3,﹣2,﹣1 B.3,2,﹣1 C.﹣3,﹣2,1 D.3,﹣2,1
【解答】解:一元二次方程3x2=2x﹣1变为一般形式为:一元二次方程3x2﹣2x+1=0,
二次项系数是3、一次项系数是﹣2、常数项1,
故选:D.
2.(3分)如图是一个水管的三叉接头,它的左视图是( )
A. B. C. D.
【解答】解:它的左视图是下面一个圆,上面一个矩形,矩形的下面一边接到下面的圆柱了.
故选:A.
3.(3分)从编号为1~10的10个完全相同的球中,任取一球,其号码能被3整除的概率是( )
A. B. C. D.
【解答】解:∵10张已编号的球(编号为连续的自然数)有三个能整除3,
∴号码能被3整除的概率为.
故选:C.
4.(3分)方程(x﹣2)2=9的解是( )
A.x1=5,x2=﹣1 B.x1=﹣5,x2=1 C.x1=11,x2=﹣7 D.x1=﹣11,x2=7
【解答】解:开方得,x﹣2=±3
解得x1=5,x2=﹣1.
故选:A.
5.(3分)如图所示,四边形ABCD中,点E、F、G、H分别是其边AB、BC、CD、DA的中点,若四边形EFGH是矩形,则下列说法正确的是( )
A.四边形ABCD是矩形
B.四边形ABCD一定是平行四边形
C.AC⊥BD
D.AC=BD
【解答】解:∵点E、F、G、H分别是其边AB、BC、CD、DA的中点,
∴四边形EFGH一定是平行四边形,
∵AC⊥BD,∴∠HEF=90°,
∴四边形EFGH是矩形;
故选:C.
6.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )
A.正六边形 B.平行四边形 C.正三角形 D.等腰梯形
【解答】解:A、是轴对称图形,也是中心对称图形.故正确;
B、不一定是轴对称图形,是中心对称图形.故错误;
C、是轴对称图形,不是中心对称图形.故错误;
D、是轴对称图形,不是中心对称图形.故错误.
故选:A.
7.(3分)反比例函数的图象如图所示,则当x>1时,函数值y的取值范围是( )
A.y>1 B.0<y<1 C.y<2 D.0<y<2
【解答】解:∵反比例函数的图象位于一三象限,
∴在每一象限内,y随着x的增大而减小,
∵当x=1时y=2,
∴当x>1时,0<y<2,
故选:D.
8.(3分)如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若=,AD=9,则AB等于( )21·cn·jy·com
A.10 B.11 C.12 D.16
【解答】解:∵DE∥BC,
∴==,又AD=9,
∴AB=12,
故选:C.
9.(3分)用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )
A.(x﹣2)2=2 B.(x+2)2=2 C.(x﹣2)2=﹣2 D.(x﹣2)2=6
【解答】解:把方程x2﹣4x+2=0的常数项移到等号的右边,得到x2﹣4x=﹣2,
方程两边同时加上一次项系数一半的平方,得到x2﹣4x+4=﹣2+4,
配方得(x﹣2)2=2.
故选:A.
10.(3分)在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
【解答】解:反比例函数的图象上的每一条曲线上,y随x的增大而增大,
∴1﹣k<0,
∴k>1.
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.(3分)一元二次方程x2=﹣3x的解是 x1=0,x2=﹣3 .
【解答】解:x2+3x=0,
x(x+3)=0,
x=0或x+3=0,
所以x1=0,x2=﹣3.
故答案为x1=0,x2=﹣3.
12.(3分)在△ABC中,DE∥BC,若=,则= .
【解答】解:∵DE∥BC,
∴==,
故答案为:.
13.(3分)若点M(3,a﹣2),N(b,a)关于原点对称,则a+b= ﹣2 .
【解答】解:由题意,得
b=﹣3,a﹣2+a=0,
解得a=1,
a+b=﹣3+1=﹣2,
故答案为:﹣2.
14.(3分)若,则= .
【解答】解:∵,
∴﹣2=,
=2+=,
∴+1=+1,
即=.
故答案为:.
15.(3分)反比例函数y=的图象经过点(﹣2,5),那么k的值为 ﹣10 .
【解答】解:由题意,得
5=,
解得k=﹣10,
故答案为:﹣10.
16.(3分)甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .
【解答】解:甲、乙、丙三个同学排成一排拍照有以下可能:
甲乙丙,甲丙乙,乙甲丙,乙丙甲,丙甲乙,丙乙甲,全部6种情况,
有4种甲没在中间,
所以甲没排在中间的概率是=.
故答案为.
17.(3分)反比例函数y=(k>0)在第一象限内的图象如图,点M是图象上一点MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是 2 .
【解答】解:由题意得:S△MOP=|k|=1,k=±2,
又因为函数图象在一象限,所以k=2.
18.(3分)如图,在△ABC中,DE∥BC, =,△ADE的面积是8,则△ABC的面积为 18 .21世纪教育网
【解答】解;∵在△ABC中,DE∥BC,
∴△ADE∽△ABC.
∵=,
∴=()2=,
,
∴S△ABC=18,
故答案为:18.
三、解答题(本大题共66分)
19.(5分)解方程:3x(x﹣1)=2﹣2x.
【解答】解:3x(x﹣1)+2(x﹣1)=0,
(x﹣1)(3x+2)=0,
∴x﹣1=0,3x+2=0,
解得x1=1,x2=﹣.
20.(6分)已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.【21·世纪·教育·网】
【解答】证明:∵ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵EB=DF,
∴△ABE≌△ADF,
∴AE=AF,
∴∠AEF=∠AFE.
21.(6分)红花中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛.
(1)请用树状图或列表法列举出各种可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
【解答】解:(1)画树状图得:
则共有12种等可能的结果;
(2)∵恰好选派一男一女两位同学参赛的有8种情况,
∴恰好选派一男一女两位同学参赛的概率为: =.
22.(6分)如图,△ABC中,∠B=90°,AB=BC,AD是△ABC的角平分线,若BD=1,求DC的长.21·世纪*教育网
【解答】解:
过D作DE⊥AC于E,
∵△ABC中,∠B=90°,AD是△ABC的角平分线,BD=1,
∴DE=BD=1,
∵∠B=90°,AB=BC,
∴∠C=∠BAC=45°,
在Rt△DEC中,sin45°=,
∴DC==.
23.(6分)如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.www-2-1-cnjy-com
【解答】证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,
∴平行四边形OBEC是矩形.
24.(7分)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.2-1-c-n-j-y
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?21*cnjy*com
【解答】解:(1)设该种商品每次降价的百分率为x%,
依题意得:400×(1﹣x%)2=324,
解得:x=10,或x=190(舍去).
答:该种商品每次降价的百分率为10%.
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100﹣m)件,
第一次降价后的单件利润为:400×(1﹣10%)﹣300=60(元/件);
第二次降价后的单件利润为:324﹣300=24(元/件).
依题意得:60m+24×(100﹣m)=36m+2400≥3210,
解得:m≥22.5.
∴m≥23.
答:为使两次降价销售的总利润不少于3210元.第一次降价后至少要售出该种商品23件.
25.(7分)如图,某学校要修建一个矩形ABCD的花圃,花圃的一边AD靠教学楼,其它三边用总长为24米的篱笆围成,设AB边的长为x(单位:米),矩形花圃ABCD的面积为S(单位:平方米).【21cnj*y.co*m】
(1)求S与x之间的函数关系式(不必写出自变量x的取值范围);
(2)当x取多少时,矩形花圃ABCD的面积最大,最大的面积为多少?
【解答】解:(1)∵AB=x,AB+BC+CD=24,
∴BC=24﹣2x,
则S=(24﹣2x)×x=﹣2x2+24x;
(2)S=﹣2x2+24x=﹣2(x﹣6)2+72,
∵a=﹣2<0,
∴函数有最大值,
故当x=6时,y有最大值72,
答:当x=6时,矩形花圃面积最大,最大面积为72平方米.
26.(7分)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,6),B(3,n)两点.21*教*育*名*师
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣<0的x的取值范围.
【解答】解:(1)将A(m,6),B(3,n)两点分别代入y=,
得:m=1,n=2,
则点A(1,6)、B(3,2),
将点A、B坐标代入y=kx+b得:,
解得:,
∴一次函数的解析式为y=﹣2x+8;
(2)由图象可知是0<x<1或x>3,
即kx+b﹣<0的解集为0<x<1或x>3.
27.(7分)如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.21-cnjy*com
【解答】解:过C作CE⊥AB于E,
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,
∴四边形CDBE为矩形,
∴BD=CE=21,CD=BE=2,
设AE=x,则1:1.5=x:21,
解得x=14,
∴旗杆的高AB=AE+BE=14+2=16米.
28.(9分)(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;21cnjy.com
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.
【解答】(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠CDF=90°,
∵∠ADC=90°,
∴∠FDC=90°.
∴∠B=∠FDC,
∵BE=DF,
∴△CBE≌△CDF(SAS).
∴CE=CF.
(2)证明:如图2,延长AD至F,使DF=BE,连接CF.
由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠ECF=∠BCD=90°,
又∠GCE=45°,
∴∠GCF=∠GCE=45°.
∵CE=CF,GC=GC,
∴△ECG≌△FCG.
∴GE=GF,
∴GE=GF=DF+GD=BE+GD.
(3)解:如图3,过C作CG⊥AD,交AD延长线于G.
在直角梯形ABCD中,
∵AD∥BC,
∴∠A=∠B=90°,
又∵∠CGA=90°,AB=BC,
∴四边形ABCG为正方形.
∴AG=BC.…(7分)
∵∠DCE=45°,
根据(1)(2)可知,ED=BE+DG.…(8分)
∴10=4+DG,
即DG=6.
设AB=x,则AE=x﹣4,AD=x﹣6,
在Rt△AED中,
∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.
解这个方程,得:x=12或x=﹣2(舍去).…(9分)
∴AB=12.
∴S梯形ABCD=(AD+BC)?AB=×(6+12)×12=108.
即梯形ABCD的面积为108.…(10分)
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)关于x的一元二次方程3x2=2x﹣1的二次项系数、一次项系数、常数项分别是( )
A.3,﹣2,﹣1 B.3,2,﹣1 C.﹣3,﹣2,1 D.3,﹣2,1
2.(3分)如图是一个水管的三叉接头,它的左视图是( )
A. B. C. D.
3.(3分)从编号为1~10的10个完全相同的球中,任取一球,其号码能被3整除的概率是( )
A. B. C. D.
4.(3分)方程(x﹣2)2=9的解是( )
A.x1=5,x2=﹣1 B.x1=﹣5,x2=1 C.x1=11,x2=﹣7 D.x1=﹣11,x2=7
5.(3分)如图所示,四边形ABCD中,点E、F、G、H分别是其边AB、BC、CD、DA的中点,若四边形EFGH是矩形,则下列说法正确的是( )
A.四边形ABCD是矩形
B.四边形ABCD一定是平行四边形
C.AC⊥BD
D.AC=BD
6.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )
A.正六边形 B.平行四边形 C.正三角形 D.等腰梯形
7.(3分)反比例函数的图象如图所示,则当x>1时,函数值y的取值范围是( )
A.y>1 B.0<y<1 C.y<2 D.0<y<2
8.(3分)如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若=,AD=9,则AB等于( )21教育网
A.10 B.11 C.12 D.16
9.(3分)用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )
A.(x﹣2)2=2 B.(x+2)2=2 C.(x﹣2)2=﹣2 D.(x﹣2)2=6
10.(3分)在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
二、填空题(本大题共8小题,每小题3分,共24分)
11.(3分)一元二次方程x2=﹣3x的解是 .
12.(3分)在△ABC中,DE∥BC,若=,则= .
13.(3分)若点M(3,a﹣2),N(b,a)关于原点对称,则a+b= .
14.(3分)若,则= .
15.(3分)反比例函数y=的图象经过点(﹣2,5),那么k的值为 .
16.(3分)甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .
17.(3分)反比例函数y=(k>0)在第一象限内的图象如图,点M是图象上一点MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是 .
18.(3分)如图,在△ABC中,DE∥BC, =,△ADE的面积是8,则△ABC的面积为 .2·1·c·n·j·y
三、解答题(本大题共66分)
19.(5分)解方程:3x(x﹣1)=2﹣2x.
20.(6分)已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.【21教育名师】
21.(6分)红花中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛.
(1)请用树状图或列表法列举出各种可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
22.(6分)如图,△ABC中,∠B=90°,AB=BC,AD是△ABC的角平分线,若BD=1,求DC的长.www.21-cn-jy.com
23.(6分)如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.【21教育】
24.(7分)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?
25.(7分)如图,某学校要修建一个矩形ABCD的花圃,花圃的一边AD靠教学楼,其它三边用总长为24米的篱笆围成,设AB边的长为x(单位:米),矩形花圃ABCD的面积为S(单位:平方米).
(1)求S与x之间的函数关系式(不必写出自变量x的取值范围);
(2)当x取多少时,矩形花圃ABCD的面积最大,最大的面积为多少?
26.(7分)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣<0的x的取值范围.
27.(7分)如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.
28.(9分)(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.
2016-2017学年黑龙江省大庆市杜尔伯特县八年级(下)期末数学试卷(五四学制)
参考答案与试题解析
一、选择题(本大题共10小题,每小题3分,共30分)
1.(3分)关于x的一元二次方程3x2=2x﹣1的二次项系数、一次项系数、常数项分别是( )
A.3,﹣2,﹣1 B.3,2,﹣1 C.﹣3,﹣2,1 D.3,﹣2,1
【解答】解:一元二次方程3x2=2x﹣1变为一般形式为:一元二次方程3x2﹣2x+1=0,
二次项系数是3、一次项系数是﹣2、常数项1,
故选:D.
2.(3分)如图是一个水管的三叉接头,它的左视图是( )
A. B. C. D.
【解答】解:它的左视图是下面一个圆,上面一个矩形,矩形的下面一边接到下面的圆柱了.
故选:A.
3.(3分)从编号为1~10的10个完全相同的球中,任取一球,其号码能被3整除的概率是( )
A. B. C. D.
【解答】解:∵10张已编号的球(编号为连续的自然数)有三个能整除3,
∴号码能被3整除的概率为.
故选:C.
4.(3分)方程(x﹣2)2=9的解是( )
A.x1=5,x2=﹣1 B.x1=﹣5,x2=1 C.x1=11,x2=﹣7 D.x1=﹣11,x2=7
【解答】解:开方得,x﹣2=±3
解得x1=5,x2=﹣1.
故选:A.
5.(3分)如图所示,四边形ABCD中,点E、F、G、H分别是其边AB、BC、CD、DA的中点,若四边形EFGH是矩形,则下列说法正确的是( )
A.四边形ABCD是矩形
B.四边形ABCD一定是平行四边形
C.AC⊥BD
D.AC=BD
【解答】解:∵点E、F、G、H分别是其边AB、BC、CD、DA的中点,
∴四边形EFGH一定是平行四边形,
∵AC⊥BD,∴∠HEF=90°,
∴四边形EFGH是矩形;
故选:C.
6.(3分)下列图形中,既是中心对称图形又是轴对称图形的是( )
A.正六边形 B.平行四边形 C.正三角形 D.等腰梯形
【解答】解:A、是轴对称图形,也是中心对称图形.故正确;
B、不一定是轴对称图形,是中心对称图形.故错误;
C、是轴对称图形,不是中心对称图形.故错误;
D、是轴对称图形,不是中心对称图形.故错误.
故选:A.
7.(3分)反比例函数的图象如图所示,则当x>1时,函数值y的取值范围是( )
A.y>1 B.0<y<1 C.y<2 D.0<y<2
【解答】解:∵反比例函数的图象位于一三象限,
∴在每一象限内,y随着x的增大而减小,
∵当x=1时y=2,
∴当x>1时,0<y<2,
故选:D.
8.(3分)如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC.若=,AD=9,则AB等于( )21·cn·jy·com
A.10 B.11 C.12 D.16
【解答】解:∵DE∥BC,
∴==,又AD=9,
∴AB=12,
故选:C.
9.(3分)用配方法解方程:x2﹣4x+2=0,下列配方正确的是( )
A.(x﹣2)2=2 B.(x+2)2=2 C.(x﹣2)2=﹣2 D.(x﹣2)2=6
【解答】解:把方程x2﹣4x+2=0的常数项移到等号的右边,得到x2﹣4x=﹣2,
方程两边同时加上一次项系数一半的平方,得到x2﹣4x+4=﹣2+4,
配方得(x﹣2)2=2.
故选:A.
10.(3分)在反比例函数y=的图象的每一条曲线上,y都随x的增大而增大,则k的值可以是( )
A.﹣1 B.0 C.1 D.2
【解答】解:反比例函数的图象上的每一条曲线上,y随x的增大而增大,
∴1﹣k<0,
∴k>1.
故选:D.
二、填空题(本大题共8小题,每小题3分,共24分)
11.(3分)一元二次方程x2=﹣3x的解是 x1=0,x2=﹣3 .
【解答】解:x2+3x=0,
x(x+3)=0,
x=0或x+3=0,
所以x1=0,x2=﹣3.
故答案为x1=0,x2=﹣3.
12.(3分)在△ABC中,DE∥BC,若=,则= .
【解答】解:∵DE∥BC,
∴==,
故答案为:.
13.(3分)若点M(3,a﹣2),N(b,a)关于原点对称,则a+b= ﹣2 .
【解答】解:由题意,得
b=﹣3,a﹣2+a=0,
解得a=1,
a+b=﹣3+1=﹣2,
故答案为:﹣2.
14.(3分)若,则= .
【解答】解:∵,
∴﹣2=,
=2+=,
∴+1=+1,
即=.
故答案为:.
15.(3分)反比例函数y=的图象经过点(﹣2,5),那么k的值为 ﹣10 .
【解答】解:由题意,得
5=,
解得k=﹣10,
故答案为:﹣10.
16.(3分)甲、乙、丙三位好朋友随机站成一排照合影,甲没有站在中间的概率为 .
【解答】解:甲、乙、丙三个同学排成一排拍照有以下可能:
甲乙丙,甲丙乙,乙甲丙,乙丙甲,丙甲乙,丙乙甲,全部6种情况,
有4种甲没在中间,
所以甲没排在中间的概率是=.
故答案为.
17.(3分)反比例函数y=(k>0)在第一象限内的图象如图,点M是图象上一点MP垂直x轴于点P,如果△MOP的面积为1,那么k的值是 2 .
【解答】解:由题意得:S△MOP=|k|=1,k=±2,
又因为函数图象在一象限,所以k=2.
18.(3分)如图,在△ABC中,DE∥BC, =,△ADE的面积是8,则△ABC的面积为 18 .21世纪教育网
【解答】解;∵在△ABC中,DE∥BC,
∴△ADE∽△ABC.
∵=,
∴=()2=,
,
∴S△ABC=18,
故答案为:18.
三、解答题(本大题共66分)
19.(5分)解方程:3x(x﹣1)=2﹣2x.
【解答】解:3x(x﹣1)+2(x﹣1)=0,
(x﹣1)(3x+2)=0,
∴x﹣1=0,3x+2=0,
解得x1=1,x2=﹣.
20.(6分)已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.【21·世纪·教育·网】
【解答】证明:∵ABCD是菱形,
∴AB=AD,∠B=∠D.
又∵EB=DF,
∴△ABE≌△ADF,
∴AE=AF,
∴∠AEF=∠AFE.
21.(6分)红花中学现要从甲、乙两位男生和丙、丁两位女生中,选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛.
(1)请用树状图或列表法列举出各种可能选派的结果;
(2)求恰好选派一男一女两位同学参赛的概率.
【解答】解:(1)画树状图得:
则共有12种等可能的结果;
(2)∵恰好选派一男一女两位同学参赛的有8种情况,
∴恰好选派一男一女两位同学参赛的概率为: =.
22.(6分)如图,△ABC中,∠B=90°,AB=BC,AD是△ABC的角平分线,若BD=1,求DC的长.21·世纪*教育网
【解答】解:
过D作DE⊥AC于E,
∵△ABC中,∠B=90°,AD是△ABC的角平分线,BD=1,
∴DE=BD=1,
∵∠B=90°,AB=BC,
∴∠C=∠BAC=45°,
在Rt△DEC中,sin45°=,
∴DC==.
23.(6分)如图,菱形ABCD的对角线AC、BC相交于点O,BE∥AC,CE∥DB.求证:四边形OBEC是矩形.www-2-1-cnjy-com
【解答】证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形,
又∵四边形ABCD是菱形,
∴AC⊥BD,
∴∠AOB=90°,
∴平行四边形OBEC是矩形.
24.(7分)某种商品的标价为400元/件,经过两次降价后的价格为324元/件,并且两次降价的百分率相同.2-1-c-n-j-y
(1)求该种商品每次降价的百分率;
(2)若该种商品进价为300元/件,两次降价共售出此种商品100件,为使两次降价销售的总利润不少于3210元.问第一次降价后至少要售出该种商品多少件?21*cnjy*com
【解答】解:(1)设该种商品每次降价的百分率为x%,
依题意得:400×(1﹣x%)2=324,
解得:x=10,或x=190(舍去).
答:该种商品每次降价的百分率为10%.
(2)设第一次降价后售出该种商品m件,则第二次降价后售出该种商品(100﹣m)件,
第一次降价后的单件利润为:400×(1﹣10%)﹣300=60(元/件);
第二次降价后的单件利润为:324﹣300=24(元/件).
依题意得:60m+24×(100﹣m)=36m+2400≥3210,
解得:m≥22.5.
∴m≥23.
答:为使两次降价销售的总利润不少于3210元.第一次降价后至少要售出该种商品23件.
25.(7分)如图,某学校要修建一个矩形ABCD的花圃,花圃的一边AD靠教学楼,其它三边用总长为24米的篱笆围成,设AB边的长为x(单位:米),矩形花圃ABCD的面积为S(单位:平方米).【21cnj*y.co*m】
(1)求S与x之间的函数关系式(不必写出自变量x的取值范围);
(2)当x取多少时,矩形花圃ABCD的面积最大,最大的面积为多少?
【解答】解:(1)∵AB=x,AB+BC+CD=24,
∴BC=24﹣2x,
则S=(24﹣2x)×x=﹣2x2+24x;
(2)S=﹣2x2+24x=﹣2(x﹣6)2+72,
∵a=﹣2<0,
∴函数有最大值,
故当x=6时,y有最大值72,
答:当x=6时,矩形花圃面积最大,最大面积为72平方米.
26.(7分)如图,一次函数y=kx+b与反比例函数y=(x>0)的图象交于A(m,6),B(3,n)两点.21*教*育*名*师
(1)求一次函数的解析式;
(2)根据图象直接写出kx+b﹣<0的x的取值范围.
【解答】解:(1)将A(m,6),B(3,n)两点分别代入y=,
得:m=1,n=2,
则点A(1,6)、B(3,2),
将点A、B坐标代入y=kx+b得:,
解得:,
∴一次函数的解析式为y=﹣2x+8;
(2)由图象可知是0<x<1或x>3,
即kx+b﹣<0的解集为0<x<1或x>3.
27.(7分)如图,某同学相测量旗杆的高度,他在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米,求旗杆的高度.21-cnjy*com
【解答】解:过C作CE⊥AB于E,
∵CD⊥BD,AB⊥BD,
∴∠EBD=∠CDB=∠CEB=90°,
∴四边形CDBE为矩形,
∴BD=CE=21,CD=BE=2,
设AE=x,则1:1.5=x:21,
解得x=14,
∴旗杆的高AB=AE+BE=14+2=16米.
28.(9分)(1)如图1,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.求证:CE=CF;21cnjy.com
(2)如图2,在正方形ABCD中,E是AB上一点,G是AD上一点,如果∠GCE=45°,请你利用(1)的结论证明:GE=BE+GD.
(3)运用(1)(2)解答中所积累的经验和知识,完成下题:
如图3,在直角梯形ABCD中,AD∥BC(BC>AD),∠B=90°,AB=BC,E是AB上一点,且∠DCE=45°,BE=4,DE=10,求直角梯形ABCD的面积.
【解答】(1)证明:∵四边形ABCD是正方形,
∴BC=CD,∠B=∠CDF=90°,
∵∠ADC=90°,
∴∠FDC=90°.
∴∠B=∠FDC,
∵BE=DF,
∴△CBE≌△CDF(SAS).
∴CE=CF.
(2)证明:如图2,延长AD至F,使DF=BE,连接CF.
由(1)知△CBE≌△CDF,
∴∠BCE=∠DCF.
∴∠BCE+∠ECD=∠DCF+∠ECD,
即∠ECF=∠BCD=90°,
又∠GCE=45°,
∴∠GCF=∠GCE=45°.
∵CE=CF,GC=GC,
∴△ECG≌△FCG.
∴GE=GF,
∴GE=GF=DF+GD=BE+GD.
(3)解:如图3,过C作CG⊥AD,交AD延长线于G.
在直角梯形ABCD中,
∵AD∥BC,
∴∠A=∠B=90°,
又∵∠CGA=90°,AB=BC,
∴四边形ABCG为正方形.
∴AG=BC.…(7分)
∵∠DCE=45°,
根据(1)(2)可知,ED=BE+DG.…(8分)
∴10=4+DG,
即DG=6.
设AB=x,则AE=x﹣4,AD=x﹣6,
在Rt△AED中,
∵DE2=AD2+AE2,即102=(x﹣6)2+(x﹣4)2.
解这个方程,得:x=12或x=﹣2(舍去).…(9分)
∴AB=12.
∴S梯形ABCD=(AD+BC)?AB=×(6+12)×12=108.
即梯形ABCD的面积为108.…(10分)
同课章节目录
