第20章 数据的分析单元测试试题(含解析)
文档属性
| 名称 | 第20章 数据的分析单元测试试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 733.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-05 08:18:25 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
人教版九年级上册第20章数据的分析
单元测试
(时间100分钟,总分100分)
一、选择题(共10小题,每小题3分,满分30分)
1.在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的平分分别为:90,85,90,80,95,则这组数据的众数是( )
A.95 B.90 C.85 D.80
2.某市测得一周PM2.5的日均值如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是 ( )
A.50和50 B.50和40 C.40和50 D.40和40
3.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( )
A.40 B.42 C.38 D.2
4.关于2,6,1,10,6的这组数据,下列说法正确的是 ( )
A.这组数据的众数是6 B.这组数据的中位数是1
C.这组数据的平均数是6 D.这组数据的方差是10
5.在某次数学测验中,随机抽取了10份试卷,其成绩如下:72,77,79,81,81,81,83,83,85,89,则这组数据的众数、中位数分别为( )
A.81,82 B.83,81 C.81,81 D.83,82
6.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5 B.8,9 C.16,8.5 D.8,8.5
7.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定9名同学参加决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
A.众数 B.平均数 C.中位数 D.方差
8.贵阳市“阳光小区”开展“节约用水, ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上月的用水量进行比较,统计出节水情况如下表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 2 2 4 1 1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5 B.0.5和0.5 C.0.47和4 D.0.5和4
9.某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
动时间(小时) 3 3.5 4 4.5
人数 1 1 2 1
A.中位数是4,平均数是3.75 B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8 D.众数是2,平均数是3.8
10.某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
二、填空(共8个小题,每题3分,共24分)
11.在统计量平均数、众数、频率、方差中,反映一组数据波动情况的是 .
12. 为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 分.
13.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为__________或__________.
14.在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 ,众数是 .
15.为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 分.
16.小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步) 1.1 1.2 1.3 1.4 1.5
天数 3 7 5 12 3
在每天所走的步数这组数据中,众数和中位数分别是 .
17.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 .21cnjy.com
18. 甲、乙两班举行电脑汉字输入速度比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级 人数 中位数 方差 平均字数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩的波动情况比乙班的成绩的波动大.上述结论正确的是__________(填序号).21·cn·jy·com
三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
20.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:2-1-c-n-j-y
表1 演讲答辩得分表(单位:分)
A B C D E
甲 90 92 94 95 88
乙 89 86 87 94 91
表2 民主测评票统计表(单位:张)
“好”票数 “较好”票数 “一般”票数
甲 40 7 3
乙 42 4 4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
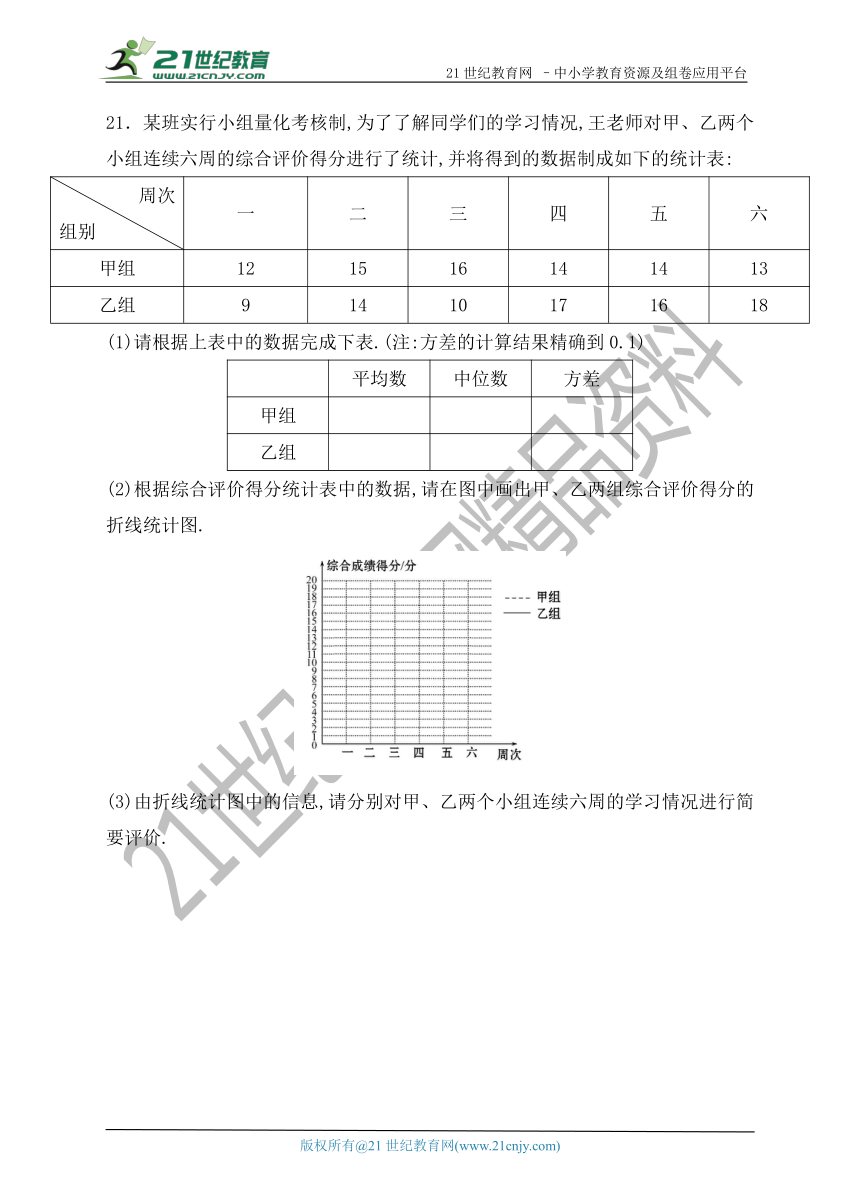
21.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次组别 一 二 三 四 五 六
甲组 12 15 16 14 14 13
乙组 9 14 10 17 16 18
(1)请根据上表中的数据完成下表.(注:方差的计算结果精确到0.1)
平均数 中位数 方差
甲组
乙组
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图.
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况进行简要评价.
22.公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:www.21-cn-jy.com
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员销售量的平均数、中位数、众数(直接写出结果,不要求过程);
(2)假设销售部把每位销售人员的月销售定额规定为320件,你认为是否合理,为什么?如果不合理,请你从表中选一个较合理的销售定额,并说明理由.
23.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
质量(g) 73 74 75 76 77 78
甲的数量 2 4 4 3 1 1
乙的数量 2 3 6 2 1 1
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是 g;乙厂抽取质量的众数是 g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数乙=75,方差≈1.73.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
23.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:21·世纪*教育网
候选人 笔试 口试 得票
甲 85 83 90
乙 80 85 92
(1)如果按笔试占总成绩20%,口试占30%,得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
24.某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.2·1·c·n·j·y
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
参考答案:
一、选择题(共10小题,每小题3分,满分30分)
1.在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的平分分别为:90,85,90,80,95,则这组数据的众数是( )
A.95 B.90 C.85 D.80
【分析】众数指一组数据中出现次数最多的数据,根据众数的定义就可以求解.
【解答】解:数据90出现了两次,次数最多,所以这组数据的众数是90.
故选B.
2.某市测得一周PM2.5的日均值如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是 ( )21*cnjy*com
A.50和50 B.50和40 C.40和50 D.40和40
【解析】选A.从小到大排列此数据为:37,40,40,50,50,50,75,数据50出现了三次最多,所以50为众数;50处在第4位是中位数.【21·世纪·教育·网】
3.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( )【21cnj*y.co*m】
A.40 B.42 C.38 D.2
分析: 根据所有数据均减去40后平均数也减去40,从而得出答案.
解:一组数据中的每一个数减去40后的平均数是2,则原数据的平均数是42;
故选B.
4.关于2,6,1,10,6的这组数据,下列说法正确的是 ( )
A.这组数据的众数是6 B.这组数据的中位数是1
C.这组数据的平均数是6 D.这组数据的方差是10
【解析】选A.∵在这组数据中,数据6出现了两次,次数最多,∴这组数据的众数是6,故A项正确;∵数据按照从小到大的顺序排列为:1,2,6,6,10,∴这组数据的中位数为6,故B项错误;∵=(1+2+6+6+10)=5,∴这组数据的平均数是5,故C项错误;∵s2=[(1-5)2+(2-5)2+(6-5)2+(6-5)2+(10-5)2]=10.4,∴这组数据的方差是10.4,故D项错误.【21教育名师】
5.在某次数学测验中,随机抽取了10份试卷,其成绩如下:72,77,79,81,81,81,83,83,85,89,则这组数据的众数、中位数分别为( )
A.81,82 B.83,81 C.81,81 D.83,82
分析: 根据众数与中位数的定义分别进行解答即可.
解:∵81出现了3次,出现的次数最多,
∴这组数据的众数是81,
把这组数据从小到大排列为72,77,79,81,81,81,83,83,85,89,
最中间两个数的平均数是:(81+81)÷2=81,
则这组数据的中位数是81;
故选C.
6.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5 B.8,9 C.16,8.5 D.8,8.5
【分析】根据中位数、众数的概念分别求得这组数据的中位数、众数,由图可知锻炼时间超过8小时的有14+7=21人.【21教育】
【解答】解:众数是一组数据中出现次数最多的数,即8;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数,由中位数的定义可知,这组数据的中位数是9;
故选B.
7.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定9名同学参加决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
A.众数 B.平均数 C.中位数 D.方差
分析: 9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
解:由于总共有9个人,且他们的分数互不相同,第5名的成绩是中位数,要判断是否进入前5名,故应知道自已的成绩和中位数.
故选C.
8.贵阳市“阳光小区”开展“节约用水, ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上月的用水量进行比较,统计出节水情况如下表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 2 2 4 1 1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5 B.0.5和0.5 C.0.47和4 D.0.5和4
【分析】找中位数要把数据按从小到大的顺序 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )排列,位于最中间的一个数或两个数的平均数为中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.
解:这10个数据的平均数为 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )=0.47,
中位数为 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )=0.5,
故选:A
9. 某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
动时间(小时) 3 3.5 4 4.5
人数 1 1 2 1
A.中位数是4,平均数是3.75 B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8 D.众数是2,平均数是3.8
分析: 根据众数、平均数和中位数的概念求解.
解:这组数据中4出现的次数最多,众数为4,
∵共有5个人,
∴第3个人的劳动时间为中位数,
故中位数为:4,
平均数为:=3.8.
故选C.
10..某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
分析:根据方差的计算公式求出丁的成绩的方差,根据方差的性质解答即可.
解:由图可知丁射击10次的成绩为:8、8、9、7、8、8、9、7、8、8,
则丁的成绩的平均数为:×(8+8+9+7+8+8+9+7+8+8)=8,
丁的成绩的方差为:×[(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2]=0.4,
∵丁的成绩的方差最小,
∴丁的成绩最稳定,
∴参赛选手应选丁,
故选:D.
二、填空(共8个小题,每题3分,共24分)
11.在统计量平均数、众数、频率、方差中,反映一组数据波动情况的是 。
【分析】根据方差和标准差的意义:体现数据的稳定性,集中程度;方差越小,数据越稳定.
【解答】解:由于方差和标准差反映数据的波动情况.
12. 为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 135 分.
【分析】根据中位数的定义,把13个数据从大到小排列后,中位数是第7个数.
【解答】解:∵13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分,
∴第7个数是135分,
∴中位数为135分;
故答案为135.
13.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为__________或__________.
【解析】因为这三个不相等的正整数的中位数是3,
设这三个正整数为a,3,b(a<3其平均数是3,有(a+b+3)=3,即a+b=6.
且a,b为正整数,故a可取1,2,分别求得b的值为5,4.故这三个数分别为1,3,5或2,3,4.
答案:1,3,5 2,3,4(或2,3,4 1,3,5)
14.在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 92 ,众数是 95 .
【分析】环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数.
【解答】解:这组数据从小到大排列为:83,85,90,92,95,95,96.则中位数是:92;
众数是95.
故答案是:92,95.
15.为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 135 分.
【分析】根据中位数的定义,把13个数据从大到小排列后,中位数是第7个数.
【解答】解:∵13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分,
∴第7个数是135分,
∴中位数为135分;
故答案为135.
16.小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步) 1.1 1.2 1.3 1.4 1.5
天数 3 7 5 12 3
在每天所走的步数这组数据中,众数和中位数分别是 1.4,1.35 .
【分析】把这组数据按照从小到大的顺序排列,第15、16个数的平均数是中位数,在这组数据中出现次数最多的是1.4,得到这组数据的众数.
【解答】解:要求一组数据的中位数,
把这组数据按照从小到大的顺序排列,第4、5个两个数的平均数是(1.3+1.4)÷2=1.35,
所以中位数是1.35,
在这组数据中出现次数最多的是1.4,
即众数是1.4.
故答案为:1.4;1.35.
17.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 2 .21教育网
【分析】运用方差公式S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2],代入数据求出即可.
【解答】解:五次射击的平均成绩为=(5+7+8+6+9)=7,
方差S2= [(5﹣7)2+(8﹣7)2+(7﹣7)2+(6﹣7)2+(9﹣7)2]=2.
故答案为:2.
18. 甲、乙两班举行电脑汉字输入速度比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级 人数 中位数 方差 平均字数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩的波动情况比乙班的成绩的波动大.上述结论正确的是__________(填序号).21*教*育*名*师
【解析】从表中可知,平均字数都是135,①正确;甲班的中位数是149,乙班的中位数是151,比甲班的多,而两班的人数都为55,说明乙班的优秀人数多于甲班的,②正确;甲班的方差大于乙班的,说明甲班的波动情况大,所以③也正确.
答案:①②③
三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
20. 分析: 求中位数时,要先看相关数据的总数是奇数还是偶数,本题中人数的总个数是17人,奇数,因此应该看从小到大排列后第9名运动员的成绩是多少,即为所求;要求平均数只要求出数据之和再除以总个数即可.
解:本题中人数的总个数是17人,奇数,从小到大排列后第9名运动员的成绩是1.70(米);
平均数是:(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷1721世纪教育网
=(3+4.8+3.3+5.1+7+1.8+1.85+1.9)÷17
=28.75÷17
≈1.69(米),
答:这些运动员成绩的中位数是1.70米,平均数大约是1.69米.
20.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表(单位:分)
A B C D E
甲 90 92 94 95 88
乙 89 86 87 94 91
表2 民主测评票统计表(单位:张)
“好”票数 “较好”票数 “一般”票数
甲 40 7 3
乙 42 4 4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
解:(1)甲的演讲答辩得分为=92(分),
甲的民主测评得分为40×2+7×1+3×0=87(分),
当a=0.6时,甲的综合得分为
92×(1-0.6)+87×0.6=36.8+52.2=89(分).
(2)∵乙的演讲答辩得分为=89(分),
乙的民主测评得分为42×2+4×1+4×0=88(分),
∴乙的综合得分为89(1-a)+88a.
由(1),知甲的综合得分为92(1-a)+87a.
当92(1-a)+87a>89(1-a)+88a时,则a<0.75.
又∵0.5≤a≤0.8,
∴当0.5≤a<0.75时,甲的综合得分高.
当92(1-a)+87a<89(1-a)+88a时,则a>0.75.
又∵0.5≤a≤0.8,
∴当0.75<a≤0.8时,乙的综合得分高.
21.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次组别 一 二 三 四 五 六
甲组 12 15 16 14 14 13
乙组 9 14 10 17 16 18
(1)请根据上表中的数据完成下表.(注:方差的计算结果精确到0.1)
平均数 中位数 方差
甲组
乙组
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图.
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况进行简要评价.
【解析】(1)填表如下:
平均数 中位数 方差
甲组 14 14 1.7
乙组 14 15 11.7
(2)如图:
(3)从折线图可以看出:甲组成绩相对稳定,但进步不大,且略有下降趋势;乙组成绩不够稳定,但进步较快,呈上升趋势.21-cnjy*com
22.公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员销售量的平均数、中位数、众数(直接写出结果,不要求过程);
(2)假设销售部把每位销售人员的月销售定额规定为320件,你认为是否合理,为什么?如果不合理,请你从表中选一个较合理的销售定额,并说明理由.
23.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
质量(g) 73 74 75 76 77 78
甲的数量 2 4 4 3 1 1
乙的数量 2 3 6 2 1 1
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是 g;乙厂抽取质量的众数是 g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数乙=75,方差≈1.73.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
分析: (1)利用中位数及众数的定义直接回答即可;
(2)计算甲的方差和平均数,然后比较方差及平均数,平均数相等方差较小的将被录用.
解:(1)75;75.
(2)解:=(73×2+74×4+75×4+76×3+77+78)÷15=75,
=
≈1.87,
∵=,>
∴两家加工厂的鸡腿质量大致相等,但乙加工厂的鸡腿质量更稳定.
因此快餐公司应该选购乙加工厂生产的鸡腿.
23.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:www-2-1-cnjy-com
候选人 笔试 口试 得票
甲 85 83 90
乙 80 85 92
(1)如果按笔试占总成绩20%,口试占30%,得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
解:(1)甲的成绩为:
85×20%+83×30%+90×50%=86.9(分),
乙的成绩为:
80×20%+85×30%+92×50%=87.5(分),
∵87.5>86.9,
∴乙会竞选上.
(2)甲的成绩为:
=86.6(分),
乙的成绩为:
=85.8(分),
∵85.8<86.6,
∴甲会竞选上.
24.某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
分析: (1)根据条形统计图和扇形统计图可以得到a和b的值,从而可以得到得3分的人数将条形统计图补充完整;
(2)根据第(1)问可以估计该地区此题得满分(即8分)的学生人数;
(3)根据题意可以算出L的值,从而可以判断试题的难度系数.
解:(1)由条形统计图可知0分的同学有24人,由扇形统计图可知,0分的同学占10%,
∴抽取的总人数是:24÷10%=240,
故得3分的学生数是;240﹣24﹣108﹣48=60,
∴a%=,b%=,
故答案为:25,20;
补全的条形统计图如右图所示,
(2)由(1)可得,得满分的占20%,
∴该地区此题得满分(即8分)的学生人数是:4500×20%=900人,
即该地区此题得满分(即8分)的学生数900人;
(3)由题意可得,
L===0.575,
∵0.575处于0.4<L≤0.7之间,
∴题对于该地区的九年级学生来说属于中等难度试题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
人教版九年级上册第20章数据的分析
单元测试
(时间100分钟,总分100分)
一、选择题(共10小题,每小题3分,满分30分)
1.在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的平分分别为:90,85,90,80,95,则这组数据的众数是( )
A.95 B.90 C.85 D.80
2.某市测得一周PM2.5的日均值如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是 ( )
A.50和50 B.50和40 C.40和50 D.40和40
3.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( )
A.40 B.42 C.38 D.2
4.关于2,6,1,10,6的这组数据,下列说法正确的是 ( )
A.这组数据的众数是6 B.这组数据的中位数是1
C.这组数据的平均数是6 D.这组数据的方差是10
5.在某次数学测验中,随机抽取了10份试卷,其成绩如下:72,77,79,81,81,81,83,83,85,89,则这组数据的众数、中位数分别为( )
A.81,82 B.83,81 C.81,81 D.83,82
6.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5 B.8,9 C.16,8.5 D.8,8.5
7.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定9名同学参加决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
A.众数 B.平均数 C.中位数 D.方差
8.贵阳市“阳光小区”开展“节约用水, ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上月的用水量进行比较,统计出节水情况如下表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 2 2 4 1 1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5 B.0.5和0.5 C.0.47和4 D.0.5和4
9.某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
动时间(小时) 3 3.5 4 4.5
人数 1 1 2 1
A.中位数是4,平均数是3.75 B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8 D.众数是2,平均数是3.8
10.某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
二、填空(共8个小题,每题3分,共24分)
11.在统计量平均数、众数、频率、方差中,反映一组数据波动情况的是 .
12. 为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 分.
13.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为__________或__________.
14.在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 ,众数是 .
15.为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 分.
16.小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步) 1.1 1.2 1.3 1.4 1.5
天数 3 7 5 12 3
在每天所走的步数这组数据中,众数和中位数分别是 .
17.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 .21cnjy.com
18. 甲、乙两班举行电脑汉字输入速度比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级 人数 中位数 方差 平均字数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩的波动情况比乙班的成绩的波动大.上述结论正确的是__________(填序号).21·cn·jy·com
三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
20.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:2-1-c-n-j-y
表1 演讲答辩得分表(单位:分)
A B C D E
甲 90 92 94 95 88
乙 89 86 87 94 91
表2 民主测评票统计表(单位:张)
“好”票数 “较好”票数 “一般”票数
甲 40 7 3
乙 42 4 4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
21.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次组别 一 二 三 四 五 六
甲组 12 15 16 14 14 13
乙组 9 14 10 17 16 18
(1)请根据上表中的数据完成下表.(注:方差的计算结果精确到0.1)
平均数 中位数 方差
甲组
乙组
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图.
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况进行简要评价.
22.公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:www.21-cn-jy.com
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员销售量的平均数、中位数、众数(直接写出结果,不要求过程);
(2)假设销售部把每位销售人员的月销售定额规定为320件,你认为是否合理,为什么?如果不合理,请你从表中选一个较合理的销售定额,并说明理由.
23.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
质量(g) 73 74 75 76 77 78
甲的数量 2 4 4 3 1 1
乙的数量 2 3 6 2 1 1
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是 g;乙厂抽取质量的众数是 g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数乙=75,方差≈1.73.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
23.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:21·世纪*教育网
候选人 笔试 口试 得票
甲 85 83 90
乙 80 85 92
(1)如果按笔试占总成绩20%,口试占30%,得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
24.某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.2·1·c·n·j·y
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
参考答案:
一、选择题(共10小题,每小题3分,满分30分)
1.在学校举行“阳光少年,励志青春”的演讲比赛中,五位评委给选手小明的平分分别为:90,85,90,80,95,则这组数据的众数是( )
A.95 B.90 C.85 D.80
【分析】众数指一组数据中出现次数最多的数据,根据众数的定义就可以求解.
【解答】解:数据90出现了两次,次数最多,所以这组数据的众数是90.
故选B.
2.某市测得一周PM2.5的日均值如下:50,40,75,50,37,50,40,这组数据的中位数和众数分别是 ( )21*cnjy*com
A.50和50 B.50和40 C.40和50 D.40和40
【解析】选A.从小到大排列此数据为:37,40,40,50,50,50,75,数据50出现了三次最多,所以50为众数;50处在第4位是中位数.【21·世纪·教育·网】
3.将一组数据中的每一个数减去40后,所得新的一组数据的平均数是2,则原来那组数据的平均数是( )【21cnj*y.co*m】
A.40 B.42 C.38 D.2
分析: 根据所有数据均减去40后平均数也减去40,从而得出答案.
解:一组数据中的每一个数减去40后的平均数是2,则原数据的平均数是42;
故选B.
4.关于2,6,1,10,6的这组数据,下列说法正确的是 ( )
A.这组数据的众数是6 B.这组数据的中位数是1
C.这组数据的平均数是6 D.这组数据的方差是10
【解析】选A.∵在这组数据中,数据6出现了两次,次数最多,∴这组数据的众数是6,故A项正确;∵数据按照从小到大的顺序排列为:1,2,6,6,10,∴这组数据的中位数为6,故B项错误;∵=(1+2+6+6+10)=5,∴这组数据的平均数是5,故C项错误;∵s2=[(1-5)2+(2-5)2+(6-5)2+(6-5)2+(10-5)2]=10.4,∴这组数据的方差是10.4,故D项错误.【21教育名师】
5.在某次数学测验中,随机抽取了10份试卷,其成绩如下:72,77,79,81,81,81,83,83,85,89,则这组数据的众数、中位数分别为( )
A.81,82 B.83,81 C.81,81 D.83,82
分析: 根据众数与中位数的定义分别进行解答即可.
解:∵81出现了3次,出现的次数最多,
∴这组数据的众数是81,
把这组数据从小到大排列为72,77,79,81,81,81,83,83,85,89,
最中间两个数的平均数是:(81+81)÷2=81,
则这组数据的中位数是81;
故选C.
6.如图是根据某班40名同学一周的体育锻炼情况绘制的条形统计图.那么该班40名同学一周参加体育锻炼时间的众数、中位数分别是( )
A.16,10.5 B.8,9 C.16,8.5 D.8,8.5
【分析】根据中位数、众数的概念分别求得这组数据的中位数、众数,由图可知锻炼时间超过8小时的有14+7=21人.【21教育】
【解答】解:众数是一组数据中出现次数最多的数,即8;
而将这组数据从小到大的顺序排列后,处于中间位置的那个数,由中位数的定义可知,这组数据的中位数是9;
故选B.
7.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定9名同学参加决赛,他们的决赛成绩各不相同,其中小辉已经知道自己的成绩,但能否进前5名,他还必须清楚这9名同学成绩的( )
A.众数 B.平均数 C.中位数 D.方差
分析: 9人成绩的中位数是第5名的成绩.参赛选手要想知道自己是否能进入前5名,只需要了解自己的成绩以及全部成绩的中位数,比较即可.
解:由于总共有9个人,且他们的分数互不相同,第5名的成绩是中位数,要判断是否进入前5名,故应知道自已的成绩和中位数.
故选C.
8.贵阳市“阳光小区”开展“节约用水, ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上月的用水量进行比较,统计出节水情况如下表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 2 2 4 1 1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5 B.0.5和0.5 C.0.47和4 D.0.5和4
【分析】找中位数要把数据按从小到大的顺序 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )排列,位于最中间的一个数或两个数的平均数为中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.
解:这10个数据的平均数为 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )=0.47,
中位数为 ( http: / / www.21cnjy.com" \o "欢迎登陆21世纪教育网 )=0.5,
故选:A
9. 某小组5名同学在一周内参加家务劳动的时间如表所示,关于“劳动时间”的这组数据,以下说法正确的是( )
动时间(小时) 3 3.5 4 4.5
人数 1 1 2 1
A.中位数是4,平均数是3.75 B.众数是4,平均数是3.75
C.中位数是4,平均数是3.8 D.众数是2,平均数是3.8
分析: 根据众数、平均数和中位数的概念求解.
解:这组数据中4出现的次数最多,众数为4,
∵共有5个人,
∴第3个人的劳动时间为中位数,
故中位数为:4,
平均数为:=3.8.
故选C.
10..某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
分析:根据方差的计算公式求出丁的成绩的方差,根据方差的性质解答即可.
解:由图可知丁射击10次的成绩为:8、8、9、7、8、8、9、7、8、8,
则丁的成绩的平均数为:×(8+8+9+7+8+8+9+7+8+8)=8,
丁的成绩的方差为:×[(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2]=0.4,
∵丁的成绩的方差最小,
∴丁的成绩最稳定,
∴参赛选手应选丁,
故选:D.
二、填空(共8个小题,每题3分,共24分)
11.在统计量平均数、众数、频率、方差中,反映一组数据波动情况的是 。
【分析】根据方差和标准差的意义:体现数据的稳定性,集中程度;方差越小,数据越稳定.
【解答】解:由于方差和标准差反映数据的波动情况.
12. 为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 135 分.
【分析】根据中位数的定义,把13个数据从大到小排列后,中位数是第7个数.
【解答】解:∵13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分,
∴第7个数是135分,
∴中位数为135分;
故答案为135.
13.已知三个不相等的正整数的平均数、中位数都是3,则这三个数分别为__________或__________.
【解析】因为这三个不相等的正整数的中位数是3,
设这三个正整数为a,3,b(a<3
且a,b为正整数,故a可取1,2,分别求得b的值为5,4.故这三个数分别为1,3,5或2,3,4.
答案:1,3,5 2,3,4(或2,3,4 1,3,5)
14.在环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数是 92 ,众数是 95 .
【分析】环保整治行动中,某市环保局对辖区内的单位进行了抽样调查,他们的综合得分如下:95,85,83,95,92,90,96,则这组数据的中位数.
【解答】解:这组数据从小到大排列为:83,85,90,92,95,95,96.则中位数是:92;
众数是95.
故答案是:92,95.
15.为了了解某班数学成绩情况,抽样调查了13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分.则这组数据的中位数为 135 分.
【分析】根据中位数的定义,把13个数据从大到小排列后,中位数是第7个数.
【解答】解:∵13份试卷成绩,结果如下:3个140分,4个135分,2个130分,2个120分,1个100分,1个80分,
∴第7个数是135分,
∴中位数为135分;
故答案为135.
16.小明的爸爸是个“健步走”运动爱好者,他用手机软件记录了某个月(30天)每天健步走的步数,并将记录结果绘制成了如下统计表:
步数(万步) 1.1 1.2 1.3 1.4 1.5
天数 3 7 5 12 3
在每天所走的步数这组数据中,众数和中位数分别是 1.4,1.35 .
【分析】把这组数据按照从小到大的顺序排列,第15、16个数的平均数是中位数,在这组数据中出现次数最多的是1.4,得到这组数据的众数.
【解答】解:要求一组数据的中位数,
把这组数据按照从小到大的顺序排列,第4、5个两个数的平均数是(1.3+1.4)÷2=1.35,
所以中位数是1.35,
在这组数据中出现次数最多的是1.4,
即众数是1.4.
故答案为:1.4;1.35.
17.在一次射击训练中,某位选手五次射击的环数分别为5,8,7,6,9,则这位选手五次射击环数的方差为 2 .21教育网
【分析】运用方差公式S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2],代入数据求出即可.
【解答】解:五次射击的平均成绩为=(5+7+8+6+9)=7,
方差S2= [(5﹣7)2+(8﹣7)2+(7﹣7)2+(6﹣7)2+(9﹣7)2]=2.
故答案为:2.
18. 甲、乙两班举行电脑汉字输入速度比赛,参加学生每分钟输入汉字的个数经统计计算后填入下表:
班级 人数 中位数 方差 平均字数
甲 55 149 191 135
乙 55 151 110 135
某同学根据上表分析得出如下结论:①甲、乙两班学生成绩的平均水平相同;②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字数≥150个为优秀);③甲班的成绩的波动情况比乙班的成绩的波动大.上述结论正确的是__________(填序号).21*教*育*名*师
【解析】从表中可知,平均字数都是135,①正确;甲班的中位数是149,乙班的中位数是151,比甲班的多,而两班的人数都为55,说明乙班的优秀人数多于甲班的,②正确;甲班的方差大于乙班的,说明甲班的波动情况大,所以③也正确.
答案:①②③
三、解答题(前3题每题7分,后三题分别为8、8、9分,共46分)
19.在某一中学田径运动会上,参加男子跳高的17名运动员的成绩如表所示:
成绩(米) 1.50 1.60 1.65 1.70 1.75 1.80 1.85 1.90
人数 2 3 2 3 4 1 1 1
分别求这些运动员成绩的中位数和平均数(结果保留到小数点后第2位).
20. 分析: 求中位数时,要先看相关数据的总数是奇数还是偶数,本题中人数的总个数是17人,奇数,因此应该看从小到大排列后第9名运动员的成绩是多少,即为所求;要求平均数只要求出数据之和再除以总个数即可.
解:本题中人数的总个数是17人,奇数,从小到大排列后第9名运动员的成绩是1.70(米);
平均数是:(1.50×2+1.60×3+1.65×2+1.70×3+1.75×4+1.80+1.85+1.90)÷1721世纪教育网
=(3+4.8+3.3+5.1+7+1.8+1.85+1.9)÷17
=28.75÷17
≈1.69(米),
答:这些运动员成绩的中位数是1.70米,平均数大约是1.69米.
20.某班为了从甲、乙两位同学中选出班长,进行了一次演讲答辩与民主测评,A,B,C,D,E五位老师作为评委,对“演讲答辩”情况进行评价,全班50位同学参与了民主测评,结果如下表所示:
表1 演讲答辩得分表(单位:分)
A B C D E
甲 90 92 94 95 88
乙 89 86 87 94 91
表2 民主测评票统计表(单位:张)
“好”票数 “较好”票数 “一般”票数
甲 40 7 3
乙 42 4 4
规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评分=“好”票数×2分+“较好”票数×1分+“一般”票数×0分;综合得分=演讲答辩分×(1-a)+民主测评分×a(0.5≤a≤0.8).
(1)当a=0.6时,甲的综合得分是多少?
(2)在什么范围内,甲的综合得分高;在什么范围内,乙的综合得分高?
解:(1)甲的演讲答辩得分为=92(分),
甲的民主测评得分为40×2+7×1+3×0=87(分),
当a=0.6时,甲的综合得分为
92×(1-0.6)+87×0.6=36.8+52.2=89(分).
(2)∵乙的演讲答辩得分为=89(分),
乙的民主测评得分为42×2+4×1+4×0=88(分),
∴乙的综合得分为89(1-a)+88a.
由(1),知甲的综合得分为92(1-a)+87a.
当92(1-a)+87a>89(1-a)+88a时,则a<0.75.
又∵0.5≤a≤0.8,
∴当0.5≤a<0.75时,甲的综合得分高.
当92(1-a)+87a<89(1-a)+88a时,则a>0.75.
又∵0.5≤a≤0.8,
∴当0.75<a≤0.8时,乙的综合得分高.
21.某班实行小组量化考核制,为了了解同学们的学习情况,王老师对甲、乙两个小组连续六周的综合评价得分进行了统计,并将得到的数据制成如下的统计表:
周次组别 一 二 三 四 五 六
甲组 12 15 16 14 14 13
乙组 9 14 10 17 16 18
(1)请根据上表中的数据完成下表.(注:方差的计算结果精确到0.1)
平均数 中位数 方差
甲组
乙组
(2)根据综合评价得分统计表中的数据,请在图中画出甲、乙两组综合评价得分的折线统计图.
(3)由折线统计图中的信息,请分别对甲、乙两个小组连续六周的学习情况进行简要评价.
【解析】(1)填表如下:
平均数 中位数 方差
甲组 14 14 1.7
乙组 14 15 11.7
(2)如图:
(3)从折线图可以看出:甲组成绩相对稳定,但进步不大,且略有下降趋势;乙组成绩不够稳定,但进步较快,呈上升趋势.21-cnjy*com
22.公司销售部有销售人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售量如下:
每人销售件数 1800 510 250 210 150 120
人数 1 1 3 5 3 2
(1)求这15位营销人员销售量的平均数、中位数、众数(直接写出结果,不要求过程);
(2)假设销售部把每位销售人员的月销售定额规定为320件,你认为是否合理,为什么?如果不合理,请你从表中选一个较合理的销售定额,并说明理由.
23.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.
质量(g) 73 74 75 76 77 78
甲的数量 2 4 4 3 1 1
乙的数量 2 3 6 2 1 1
根据表中数据,回答下列问题:
(1)甲厂抽取质量的中位数是 g;乙厂抽取质量的众数是 g.
(2)如果快餐公司决定从平均数和方差两方面考虑选购,现已知抽取乙厂的样本平均数乙=75,方差≈1.73.请你帮助计算出抽取甲厂的样本平均数及方差(结果保留小数点后两位),并指出快餐公司应选购哪家加工厂的鸡腿?
分析: (1)利用中位数及众数的定义直接回答即可;
(2)计算甲的方差和平均数,然后比较方差及平均数,平均数相等方差较小的将被录用.
解:(1)75;75.
(2)解:=(73×2+74×4+75×4+76×3+77+78)÷15=75,
=
≈1.87,
∵=,>
∴两家加工厂的鸡腿质量大致相等,但乙加工厂的鸡腿质量更稳定.
因此快餐公司应该选购乙加工厂生产的鸡腿.
23.甲、乙两名大学生竞选班长,现对甲、乙两名候选人从笔试、口试、得票三个方面表现进行评分,各项成绩如表所示:www-2-1-cnjy-com
候选人 笔试 口试 得票
甲 85 83 90
乙 80 85 92
(1)如果按笔试占总成绩20%,口试占30%,得票占50%来计算各人的成绩,试判断谁会竞选上?
(2)如果将笔试、口试和得票按2∶1∶2来计算各人的成绩,那么又是谁会竞选上?
解:(1)甲的成绩为:
85×20%+83×30%+90×50%=86.9(分),
乙的成绩为:
80×20%+85×30%+92×50%=87.5(分),
∵87.5>86.9,
∴乙会竞选上.
(2)甲的成绩为:
=86.6(分),
乙的成绩为:
=85.8(分),
∵85.8<86.6,
∴甲会竞选上.
24.某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
请根据以上信息解答下列问题:
(1)填空:a= ,b= ,并把条形统计图补全;
(2)请估计该地区此题得满分(即8分)的学生人数;
(3)已知难度系数的计算公式为L=,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?
分析: (1)根据条形统计图和扇形统计图可以得到a和b的值,从而可以得到得3分的人数将条形统计图补充完整;
(2)根据第(1)问可以估计该地区此题得满分(即8分)的学生人数;
(3)根据题意可以算出L的值,从而可以判断试题的难度系数.
解:(1)由条形统计图可知0分的同学有24人,由扇形统计图可知,0分的同学占10%,
∴抽取的总人数是:24÷10%=240,
故得3分的学生数是;240﹣24﹣108﹣48=60,
∴a%=,b%=,
故答案为:25,20;
补全的条形统计图如右图所示,
(2)由(1)可得,得满分的占20%,
∴该地区此题得满分(即8分)的学生人数是:4500×20%=900人,
即该地区此题得满分(即8分)的学生数900人;
(3)由题意可得,
L===0.575,
∵0.575处于0.4<L≤0.7之间,
∴题对于该地区的九年级学生来说属于中等难度试题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
