人教版小学二年级数学上 8 组合问题课件 (共17张PPT)
文档属性
| 名称 | 人教版小学二年级数学上 8 组合问题课件 (共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-05 16:28:36 | ||
图片预览





文档简介
(共17张PPT)
02 组合问题
教材第98页
组合问题
课题引入
课题引入
有3个数5、7、9,任意选取其中2个组
成没有重复数字的两位数,能组成几个两位
数?
6个,57、59、75、79、95、97。
你能做到不重不漏吗?
可以用交换位置的方法,也可以用确定十
位或个位的方法。
教学新知
教学新知
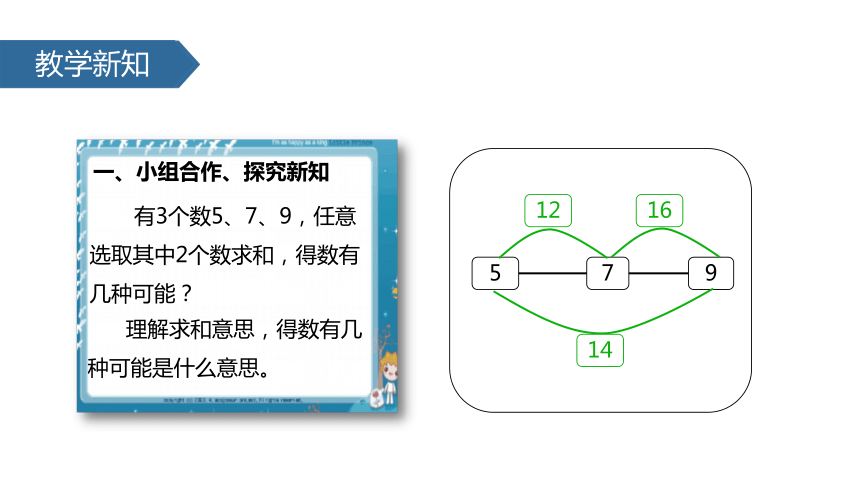
一、小组合作、探究新知
有3个数5、7、9,任意
选取其中2个数求和,得数有
几种可能?
理解求和意思,得数有几
种可能是什么意思。
5
7
9
12
16
14
教学新知
二,巩固练习、拓展思维。
看右图先猜一猜三人一共握手多
少次?再四个人为一小组,三个人握
手,一个人记录。
看来,两个人相互握手,只能算
一次刚才排数,交换数的位置,就变
成另一个数了。
知识梳理
知识点1 :排列与顺序有关,组合与顺序无关。
【例】 方方、明明和东东打棒球,他们每两人打一场,一共能打( )
场。
解析: 每两人打一场一次,那么每个人要打3-1=2场;
3个人一共打3×2=6场,但这样算每场就算成了
2次,所以要除以2。即3×(3-1)÷2=3×2÷2=3
(场)。
3
知识梳理
小结:本题考查了握手问题的实际应用,要
注意去掉重复计算的情况,如果人数比较少
可以用枚举法解答,可以用画图的方法来解
答,如果人数比较多也可以找规律,列式解
答。
小练习
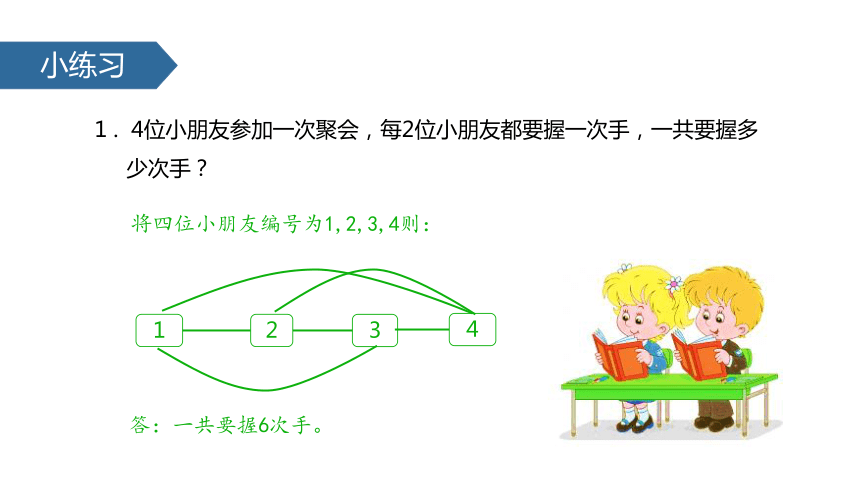
1 . 4位小朋友参加一次聚会,每2位小朋友都要握一次手,一共要握多
少次手?
将四位小朋友编号为1,2,3,4则:
1
2
3
4
答:一共要握6次手。
小练习
2 . 学期快结束了,同学们要选“三好生”,有四名同学被提名,选其中
的2个,共有几种推选结果?
小红
小明
小王
小丽
答:结果可能是:小红、小丽;小红、小王;小红、小明;小丽、小
王;小丽、小明;小王、小明;共6种结果。
课堂练习
1 . 小黑、小白和小灰三只兔朋友见面了,每两只小兔握一次手三只小
兔一共握了多少次手?
小黑 小白 小灰
答:小黑、小白、小灰,三只小兔一共握了3次手。
课堂练习
2 .小黑、小白、小红和小灰四只兔朋友见面了,每两只小兔握一
次手,四只小兔一共握了( )次手。
小黑 小白 小红 小灰
答:小黑、小白、小红、小灰,四只小兔一共握了6次手。
6
4 .小红和四个好朋友比赛踢毽子,每两个人都要赛一场,一共要进行
( )场比赛。
课堂练习
3 .小红和2个好朋友比赛踢毽子,每两个人都要赛一场,一共要进行
( )场比赛。
解析:场数有:小红、朋友1;小红、朋友2;朋友1和朋友2;总共
3场。
10
解析:场数有:小红和朋友1;小红和朋友2;小红和朋友3;小红
和朋友4;朋友1和朋友2;朋友1和朋友3;朋友1和朋友4;朋友2
和朋友3;朋友2和朋友4;朋友3和朋友4;总共10场。
3
课堂练习
5 .从5、7、9三个数字当中任意选取其中2个相加,和可能是多少? 有多少
个不同的和?
5+7=12,5+9=14 , 7+9=16,7+5=12 ,
9+5=149+7=16。
答:一共有6种可能,有三个不同。
6 .用数字4、5、6 可以组成多少个没有重复的两位数 三位数呢
答:两位数有:45、54、46、64、56、65。一共六个
三位数有:456、465、546、564、645、654。共六个
课后作业
1.填空题。
(1)方方、明明和东东打羽毛球球,每两人打一场,一共需要打
( )场。
(2)小新有2 种不同颜色的上衣(红、黄),2 种不同颜色的裤子(黑、
白),他想穿一套衣服去上学,有( )种不同的搭配方法。
(3)小红有尼龙袜、毛线袜、丝光袜共3 双,还有2 双不同的鞋子
如果她要穿上鞋和袜,可有( )种不同的穿法。
3
4
6
课后作业
2.判断题。
(1)小明拍球拍了6下,小红和小刚两人拍的比小明拍的多5下小红
和小明共拍了30下。( )
(2)每两个队进行一场比赛,4个队参加比赛,一共要比6场。( )
(3)小明在演讲比赛中获得了第1名,他和参加比赛的每个选手都
握了一次手,他记得一共握了9次手,参加比赛的一共有9个人。( )
√
×
×
拓展提高
1.用数字4、5、6 可以组成多少个没有重复的两位数 三位数呢
两位数:
45、46、54、56、64、65 。一共有6个没有重复的两
位数。
三位数:
456、465、546、564、645、654 。一共有6个没有重
复的两位数。
拓展提高
2 .有5个小朋友,要互相通一次电话,他们一共要打多少次电话
解析:第一个同学与剩下四个同学通话4次,第二个同学和剩下
的三个同学通话3次,第三个同学和剩下的两个同学通话
2次,第四个同学和最后一个同学通话1次;这五个同学
总共通话次数:4+3+2+1=10(次)。
4+3+2+1=10(次)答:他们一共通话10次。
发散思维
1 .有10 元、一张5 元、一张1 元的人民币各一张,可以组成多少种不同
的币值
选一张:10元、5元、1元,一共有三种币值。
选两张:15元、11元、6元,一共有三种币值。
选三张:16元,一共只有一种币值。
答:一共有7种币值,它们分别是:10元、5元、1元、15元、
11元、6元、16元。
02 组合问题
教材第98页
组合问题
课题引入
课题引入
有3个数5、7、9,任意选取其中2个组
成没有重复数字的两位数,能组成几个两位
数?
6个,57、59、75、79、95、97。
你能做到不重不漏吗?
可以用交换位置的方法,也可以用确定十
位或个位的方法。
教学新知
教学新知
一、小组合作、探究新知
有3个数5、7、9,任意
选取其中2个数求和,得数有
几种可能?
理解求和意思,得数有几
种可能是什么意思。
5
7
9
12
16
14
教学新知
二,巩固练习、拓展思维。
看右图先猜一猜三人一共握手多
少次?再四个人为一小组,三个人握
手,一个人记录。
看来,两个人相互握手,只能算
一次刚才排数,交换数的位置,就变
成另一个数了。
知识梳理
知识点1 :排列与顺序有关,组合与顺序无关。
【例】 方方、明明和东东打棒球,他们每两人打一场,一共能打( )
场。
解析: 每两人打一场一次,那么每个人要打3-1=2场;
3个人一共打3×2=6场,但这样算每场就算成了
2次,所以要除以2。即3×(3-1)÷2=3×2÷2=3
(场)。
3
知识梳理
小结:本题考查了握手问题的实际应用,要
注意去掉重复计算的情况,如果人数比较少
可以用枚举法解答,可以用画图的方法来解
答,如果人数比较多也可以找规律,列式解
答。
小练习
1 . 4位小朋友参加一次聚会,每2位小朋友都要握一次手,一共要握多
少次手?
将四位小朋友编号为1,2,3,4则:
1
2
3
4
答:一共要握6次手。
小练习
2 . 学期快结束了,同学们要选“三好生”,有四名同学被提名,选其中
的2个,共有几种推选结果?
小红
小明
小王
小丽
答:结果可能是:小红、小丽;小红、小王;小红、小明;小丽、小
王;小丽、小明;小王、小明;共6种结果。
课堂练习
1 . 小黑、小白和小灰三只兔朋友见面了,每两只小兔握一次手三只小
兔一共握了多少次手?
小黑 小白 小灰
答:小黑、小白、小灰,三只小兔一共握了3次手。
课堂练习
2 .小黑、小白、小红和小灰四只兔朋友见面了,每两只小兔握一
次手,四只小兔一共握了( )次手。
小黑 小白 小红 小灰
答:小黑、小白、小红、小灰,四只小兔一共握了6次手。
6
4 .小红和四个好朋友比赛踢毽子,每两个人都要赛一场,一共要进行
( )场比赛。
课堂练习
3 .小红和2个好朋友比赛踢毽子,每两个人都要赛一场,一共要进行
( )场比赛。
解析:场数有:小红、朋友1;小红、朋友2;朋友1和朋友2;总共
3场。
10
解析:场数有:小红和朋友1;小红和朋友2;小红和朋友3;小红
和朋友4;朋友1和朋友2;朋友1和朋友3;朋友1和朋友4;朋友2
和朋友3;朋友2和朋友4;朋友3和朋友4;总共10场。
3
课堂练习
5 .从5、7、9三个数字当中任意选取其中2个相加,和可能是多少? 有多少
个不同的和?
5+7=12,5+9=14 , 7+9=16,7+5=12 ,
9+5=149+7=16。
答:一共有6种可能,有三个不同。
6 .用数字4、5、6 可以组成多少个没有重复的两位数 三位数呢
答:两位数有:45、54、46、64、56、65。一共六个
三位数有:456、465、546、564、645、654。共六个
课后作业
1.填空题。
(1)方方、明明和东东打羽毛球球,每两人打一场,一共需要打
( )场。
(2)小新有2 种不同颜色的上衣(红、黄),2 种不同颜色的裤子(黑、
白),他想穿一套衣服去上学,有( )种不同的搭配方法。
(3)小红有尼龙袜、毛线袜、丝光袜共3 双,还有2 双不同的鞋子
如果她要穿上鞋和袜,可有( )种不同的穿法。
3
4
6
课后作业
2.判断题。
(1)小明拍球拍了6下,小红和小刚两人拍的比小明拍的多5下小红
和小明共拍了30下。( )
(2)每两个队进行一场比赛,4个队参加比赛,一共要比6场。( )
(3)小明在演讲比赛中获得了第1名,他和参加比赛的每个选手都
握了一次手,他记得一共握了9次手,参加比赛的一共有9个人。( )
√
×
×
拓展提高
1.用数字4、5、6 可以组成多少个没有重复的两位数 三位数呢
两位数:
45、46、54、56、64、65 。一共有6个没有重复的两
位数。
三位数:
456、465、546、564、645、654 。一共有6个没有重
复的两位数。
拓展提高
2 .有5个小朋友,要互相通一次电话,他们一共要打多少次电话
解析:第一个同学与剩下四个同学通话4次,第二个同学和剩下
的三个同学通话3次,第三个同学和剩下的两个同学通话
2次,第四个同学和最后一个同学通话1次;这五个同学
总共通话次数:4+3+2+1=10(次)。
4+3+2+1=10(次)答:他们一共通话10次。
发散思维
1 .有10 元、一张5 元、一张1 元的人民币各一张,可以组成多少种不同
的币值
选一张:10元、5元、1元,一共有三种币值。
选两张:15元、11元、6元,一共有三种币值。
选三张:16元,一共只有一种币值。
答:一共有7种币值,它们分别是:10元、5元、1元、15元、
11元、6元、16元。
