黑龙江省哈尔滨市道外区2016-2017学年七年级上学期期末考试数学试题(含答案)
文档属性
| 名称 | 黑龙江省哈尔滨市道外区2016-2017学年七年级上学期期末考试数学试题(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-05 00:00:00 | ||
图片预览

文档简介
2016——2017学年度(上)道外区期末水平测试七年级
数学试卷
一、选择题(每小题3分,共30分)
1.4的算术平方根是( )
A. 2 B. -2 C. ±2 D. ±
2.方程的解是( )
A. B. ?? C. D.
3.下列各数中是无理数的有( )
-0.333…, , , , 3, 3.1415
A.3个 B.4个 C. 5个 D. 6个21教育网
4.如果点P(﹣5,y)在第三象限,则y的取值范围是( )
A. y<0 B. y>0 C.y大于或等于0 D.y小于或等于0
5.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
A.(3,0) B.(3 ,0)或 (﹣3 ,0) C.(3,0) D.(0,3)或 (0,﹣3)
6.已知某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,;另一个亏损了20%,在这次买卖中这家商店( )21·cn·jy·com
A. 不赢不亏 B. 盈利10元 C.亏损10元 D.盈利50元
7.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为cm,可列方程( )2·1·c·n·j·y
A. B.
C. D.
8.在下列命题中,①两条直线平行,内错角相等.②相等的角是对顶角.③等角的余角相等.④在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.其中正确命题的个数是( )
A.1 B.2 C.3 D. 4
如图,AD∥BC,∠C=30°,∠ADB∶∠BDC=1∶2,
则∠DBC的度数是( )
A 45° B 30° C 50° D 36°
10.如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,
∠MNB=115°,则下列结论正确的是( )
A.∠A=∠C B.∠E=∠F C.AE∥FC D.AB∥DC
二、填空题(每小题3分,共计30分)
11. 的相反数是 .
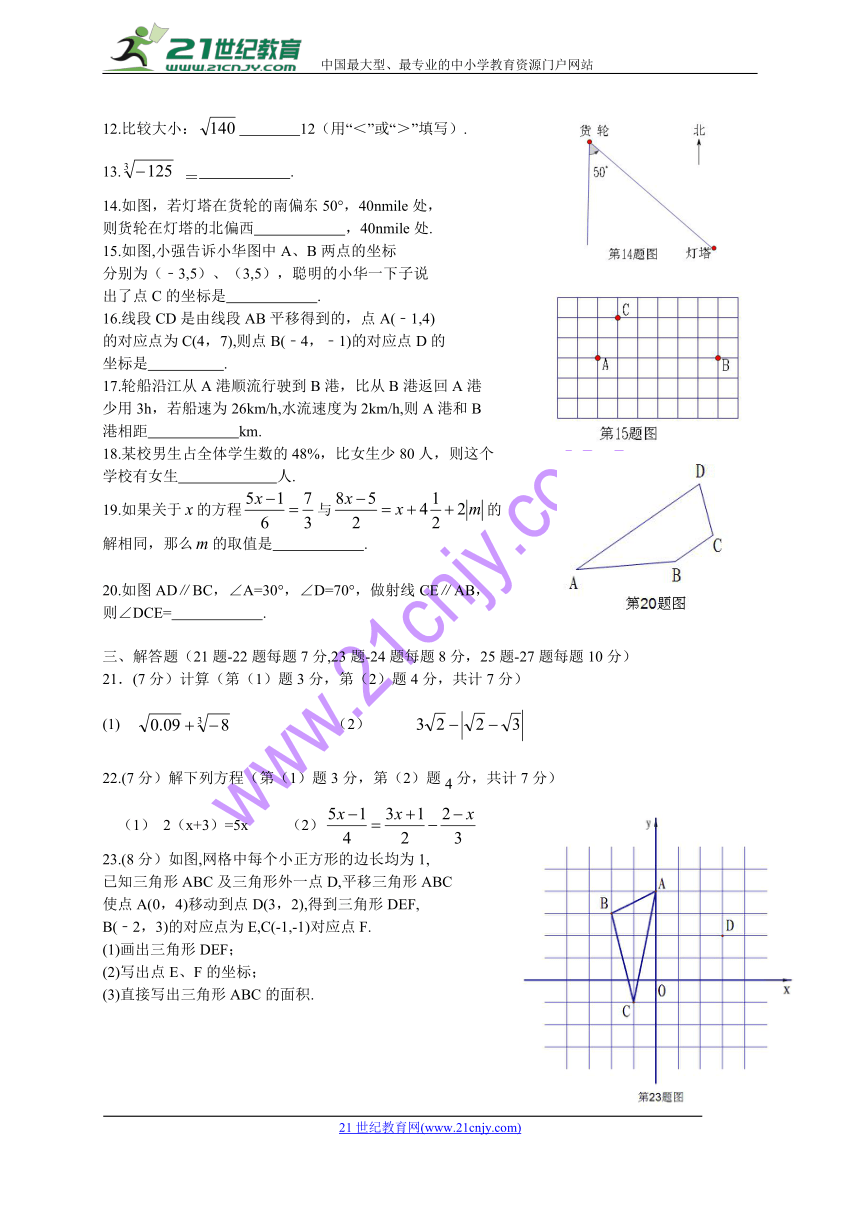
12.比较大小: 12(用“<”或“>”填写).
13. = .
14.如图,若灯塔在货轮的南偏东50°,40nmile处,
则货轮在灯塔的北偏西 ,40nmile处.
15.如图,小强告诉小华图中A、B两点的坐标
分别为(﹣3,5)、(3,5),聪明的小华一下子说
出了点C的坐标是 .
16.线段CD是由线段AB平移得到的,点A(﹣1,4)
的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的
坐标是 .
17.轮船沿江从A港顺流行驶到B港,比从B港返回A港
少用3h,若船速为26km/h,水流速度为2km/h,则A港和B
港相距 km.
某校男生占全体学生数的48%,比女生少80人,则这个
学校有女生 人.
19.如果关于的方程与的
解相同,那么的取值是 .
20.如图AD∥BC,∠A=30°,∠D=70°,做射线CE∥AB,
则∠DCE= .
三、解答题(21题-22题每题7分,23题-24题每题8分,25题-27题每题10分)
21.(7分)计算(第(1)题3分,第(2)题4分,共计7分)
(1) (2)
22.(7分)解下列方程(第(1)题3分,第(2)题4分,共计7分)
(1) 2(x+3)=5x (2)
(8分)如图,网格中每个小正方形的边长均为1,
已知三角形ABC及三角形外一点D,平移三角形ABC
使点A(0,4)移动到点D(3,2),得到三角形DEF,
B(﹣2,3)的对应点为E,C(-1,-1)对应点F.
画出三角形DEF;
写出点E、F的坐标;
直接写出三角形ABC的面积.
24.(8分)请把以下证明过程补充完整,并在下面的括号内填上推理理由:
已知:如图,∠1=∠2,∠A=∠D.
求证:∠B=∠C
证明:∵∠1=∠2,(已知)
又:∵∠1=∠3,( )
∴∠2=_______,(等量代换)
∴AE∥FD( )
∴∠A=∠BFD( )
∵∠A=∠D(已知)
∴∠D=_______(等量代换)
∴_______∥CD( )
∴∠B=∠C( )
25.(10分) 一组数: 2, 5, 8, 11,14,…(第一个数2称为第一项,第二个数5称为第二项,以此类推),通过观察这组数据规律解答下列问题:21cnjy.com
(1)第九项的数是 ;
(2)第n项是 (用含n的代数式表示);
(3)若连续的三项之和是123,求这三个连续的数各是多少?
26.(10分)列一元一次方程解应用问题:
一个蓄水池装有甲、乙两个进水管和丙一个出水管,单独开放甲管3小时可注满一池水,单独开放乙管6小时可注满一池水,单独开放丙管4小时可放尽一池水.www.21-cn-jy.com
若同时开放甲、乙、丙三个水管,几小时可注满水池?
若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需几小时可注满水池?
若甲管先开放1小时后关闭,而后同时开放乙、丙两个水管,能注满水池吗?
并说明理由.
27.10分)在同一平面内,三条直线两两分别相交于点A、B、C三点,点E是直线BC上一动点(点E不与点B、C重合),过点E分别作直线AB、AC的平行线,分别交直线AC、AB于点F、D.
(1)如图1,当点E在B、C两点之间时,求证:∠DEF=∠BAC;
(2)如图2,当点E在线段BC延长线时,试判断∠DEF与∠BAC的数量关系;
(3)如图3,点E在线段CB延长线时,∠BEF的平分线交直线AB于G,过点E作EG的垂线.交直线AB于M,点N在FE延长线上;若∠ABC=80°,∠DEM∶∠BED =2∶3, 求∠BAC的度数.
2016——2017学年度上学期期末七年级数学测试题参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
选项
A
B
A
A
B
B
D
C
C
D
填空题
题号
11
12
13
14
15
16
17
18
19
20
答案
<
-5
50o
(﹣2,7)
(1,2)
504
1040
±1
80o或100o
21.(7分)计算(第(1)题3分,第(2)题4分,共计7分)
(1) 解: =0.3(1分)+2(1分)=2.3 (1分)
(2)
22.(7分)解下列方程(第(1)题3分,第(2)题4分,共计7分))
解;(1)2x+6=5x…(1分)-3x=-6…(1分)x=2…(1分)
(2)3(5x-1)=6(3x+1)-4(2-x)…(1分)-7x=1…(2分)x=…(1分)
23.(1)画对图形(3分)。(2)E(1,1)、F(2,-3)。坐标正确(各1分)。
(3)三角形ABC的面积是个平方单位。(3分)
24 每空1分
25(1)第九项的数是26;(3分)(2)第n项是3n-1;(3分)(3)这三个数分别是38、41、44。(4分)21世纪教育网
26.解:设:
(1)三个水管同时开放小时可注满水池,根据题意得 …(1分)
化简得: …(1分) ∴三个水管同时开放4小时可注满水池 …(1分)
设:共需y小时可注满水池,根据题意得 …(1分)
解得 …(1分)∴先开放甲管1小时后,再开放乙、丙两管共需 小时可注满水池.…(1分)
设开放甲管1小时后,再开放乙、丙两管,需z小时可注满水池,根据题意得
…(1分) 解得…(1分)∵ -8<0不符合实际意义…(1分)所以先
甲管1小时后,再开放乙、丙两管不能注满水池.…(1分)
(1)如图1,证明:∵AB∥EF∴∠BAC=∠EFC…(1分)又∵AC∥DE∴∠DEF=∠EFC
…(1分)∴∠BAC=∠DEF…(1分)
∠BAC+∠DEF=180°…(2分)
解:∵AB∥EF∴∠FEC=∠ABC=80° ∠BAC=∠EFC ∵EG平分∠FEC
∴∠GEC= ∠FEC= ×80°=40°…(1分)∵EG⊥EM∴∠GEM=90°
∴∠CEM=∠GEM-∠GEC=50°…(1分)又∵∠DEM∶∠BED =2∶3∴ ∠BED =30°(1分)
∴∠FED=∠FEC+∠CED=80°+30°=110°…(1分)
∵AC∥DE∴∠FED+∠EFC=180°∴∠EFC=70°∠BAC=∠EFC =70°…(1分)
注:以上各题如有不同解法请酌情给分
数学试卷
一、选择题(每小题3分,共30分)
1.4的算术平方根是( )
A. 2 B. -2 C. ±2 D. ±
2.方程的解是( )
A. B. ?? C. D.
3.下列各数中是无理数的有( )
-0.333…, , , , 3, 3.1415
A.3个 B.4个 C. 5个 D. 6个21教育网
4.如果点P(﹣5,y)在第三象限,则y的取值范围是( )
A. y<0 B. y>0 C.y大于或等于0 D.y小于或等于0
5.若x轴上的点P到y轴的距离是3,则点P的坐标为( )
A.(3,0) B.(3 ,0)或 (﹣3 ,0) C.(3,0) D.(0,3)或 (0,﹣3)
6.已知某商店有两个进价不同的计算器都卖了80元,其中一个盈利60%,;另一个亏损了20%,在这次买卖中这家商店( )21·cn·jy·com
A. 不赢不亏 B. 盈利10元 C.亏损10元 D.盈利50元
7.一个长方形的周长为26cm,若这个长方形的长减少1cm,宽增加2cm,就可成为一个正方形,设这个长方形的长为cm,可列方程( )2·1·c·n·j·y
A. B.
C. D.
8.在下列命题中,①两条直线平行,内错角相等.②相等的角是对顶角.③等角的余角相等.④在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.其中正确命题的个数是( )
A.1 B.2 C.3 D. 4
如图,AD∥BC,∠C=30°,∠ADB∶∠BDC=1∶2,
则∠DBC的度数是( )
A 45° B 30° C 50° D 36°
10.如图,直线EF分别交CD、AB于M、N,且∠EMD=65°,
∠MNB=115°,则下列结论正确的是( )
A.∠A=∠C B.∠E=∠F C.AE∥FC D.AB∥DC
二、填空题(每小题3分,共计30分)
11. 的相反数是 .
12.比较大小: 12(用“<”或“>”填写).
13. = .
14.如图,若灯塔在货轮的南偏东50°,40nmile处,
则货轮在灯塔的北偏西 ,40nmile处.
15.如图,小强告诉小华图中A、B两点的坐标
分别为(﹣3,5)、(3,5),聪明的小华一下子说
出了点C的坐标是 .
16.线段CD是由线段AB平移得到的,点A(﹣1,4)
的对应点为C(4,7),则点B(﹣4,﹣1)的对应点D的
坐标是 .
17.轮船沿江从A港顺流行驶到B港,比从B港返回A港
少用3h,若船速为26km/h,水流速度为2km/h,则A港和B
港相距 km.
某校男生占全体学生数的48%,比女生少80人,则这个
学校有女生 人.
19.如果关于的方程与的
解相同,那么的取值是 .
20.如图AD∥BC,∠A=30°,∠D=70°,做射线CE∥AB,
则∠DCE= .
三、解答题(21题-22题每题7分,23题-24题每题8分,25题-27题每题10分)
21.(7分)计算(第(1)题3分,第(2)题4分,共计7分)
(1) (2)
22.(7分)解下列方程(第(1)题3分,第(2)题4分,共计7分)
(1) 2(x+3)=5x (2)
(8分)如图,网格中每个小正方形的边长均为1,
已知三角形ABC及三角形外一点D,平移三角形ABC
使点A(0,4)移动到点D(3,2),得到三角形DEF,
B(﹣2,3)的对应点为E,C(-1,-1)对应点F.
画出三角形DEF;
写出点E、F的坐标;
直接写出三角形ABC的面积.
24.(8分)请把以下证明过程补充完整,并在下面的括号内填上推理理由:
已知:如图,∠1=∠2,∠A=∠D.
求证:∠B=∠C
证明:∵∠1=∠2,(已知)
又:∵∠1=∠3,( )
∴∠2=_______,(等量代换)
∴AE∥FD( )
∴∠A=∠BFD( )
∵∠A=∠D(已知)
∴∠D=_______(等量代换)
∴_______∥CD( )
∴∠B=∠C( )
25.(10分) 一组数: 2, 5, 8, 11,14,…(第一个数2称为第一项,第二个数5称为第二项,以此类推),通过观察这组数据规律解答下列问题:21cnjy.com
(1)第九项的数是 ;
(2)第n项是 (用含n的代数式表示);
(3)若连续的三项之和是123,求这三个连续的数各是多少?
26.(10分)列一元一次方程解应用问题:
一个蓄水池装有甲、乙两个进水管和丙一个出水管,单独开放甲管3小时可注满一池水,单独开放乙管6小时可注满一池水,单独开放丙管4小时可放尽一池水.www.21-cn-jy.com
若同时开放甲、乙、丙三个水管,几小时可注满水池?
若甲管先开放1小时,而后同时开放乙、丙两个水管,则共需几小时可注满水池?
若甲管先开放1小时后关闭,而后同时开放乙、丙两个水管,能注满水池吗?
并说明理由.
27.10分)在同一平面内,三条直线两两分别相交于点A、B、C三点,点E是直线BC上一动点(点E不与点B、C重合),过点E分别作直线AB、AC的平行线,分别交直线AC、AB于点F、D.
(1)如图1,当点E在B、C两点之间时,求证:∠DEF=∠BAC;
(2)如图2,当点E在线段BC延长线时,试判断∠DEF与∠BAC的数量关系;
(3)如图3,点E在线段CB延长线时,∠BEF的平分线交直线AB于G,过点E作EG的垂线.交直线AB于M,点N在FE延长线上;若∠ABC=80°,∠DEM∶∠BED =2∶3, 求∠BAC的度数.
2016——2017学年度上学期期末七年级数学测试题参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
选项
A
B
A
A
B
B
D
C
C
D
填空题
题号
11
12
13
14
15
16
17
18
19
20
答案
<
-5
50o
(﹣2,7)
(1,2)
504
1040
±1
80o或100o
21.(7分)计算(第(1)题3分,第(2)题4分,共计7分)
(1) 解: =0.3(1分)+2(1分)=2.3 (1分)
(2)
22.(7分)解下列方程(第(1)题3分,第(2)题4分,共计7分))
解;(1)2x+6=5x…(1分)-3x=-6…(1分)x=2…(1分)
(2)3(5x-1)=6(3x+1)-4(2-x)…(1分)-7x=1…(2分)x=…(1分)
23.(1)画对图形(3分)。(2)E(1,1)、F(2,-3)。坐标正确(各1分)。
(3)三角形ABC的面积是个平方单位。(3分)
24 每空1分
25(1)第九项的数是26;(3分)(2)第n项是3n-1;(3分)(3)这三个数分别是38、41、44。(4分)21世纪教育网
26.解:设:
(1)三个水管同时开放小时可注满水池,根据题意得 …(1分)
化简得: …(1分) ∴三个水管同时开放4小时可注满水池 …(1分)
设:共需y小时可注满水池,根据题意得 …(1分)
解得 …(1分)∴先开放甲管1小时后,再开放乙、丙两管共需 小时可注满水池.…(1分)
设开放甲管1小时后,再开放乙、丙两管,需z小时可注满水池,根据题意得
…(1分) 解得…(1分)∵ -8<0不符合实际意义…(1分)所以先
甲管1小时后,再开放乙、丙两管不能注满水池.…(1分)
(1)如图1,证明:∵AB∥EF∴∠BAC=∠EFC…(1分)又∵AC∥DE∴∠DEF=∠EFC
…(1分)∴∠BAC=∠DEF…(1分)
∠BAC+∠DEF=180°…(2分)
解:∵AB∥EF∴∠FEC=∠ABC=80° ∠BAC=∠EFC ∵EG平分∠FEC
∴∠GEC= ∠FEC= ×80°=40°…(1分)∵EG⊥EM∴∠GEM=90°
∴∠CEM=∠GEM-∠GEC=50°…(1分)又∵∠DEM∶∠BED =2∶3∴ ∠BED =30°(1分)
∴∠FED=∠FEC+∠CED=80°+30°=110°…(1分)
∵AC∥DE∴∠FED+∠EFC=180°∴∠EFC=70°∠BAC=∠EFC =70°…(1分)
注:以上各题如有不同解法请酌情给分
同课章节目录
