人教五四版七年级(上)数学《第12章 相交线与平行线》单元测试(含答案)
文档属性
| 名称 | 人教五四版七年级(上)数学《第12章 相交线与平行线》单元测试(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 352.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-05 16:33:41 | ||
图片预览




文档简介
《相交线与平行线》单元测试
一.选择题(共13小题)
1.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
A.35° B.40° C.45° D.55°
3.如图,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,垂足为点M,PN∥OB,PN与OA相交于点N,那么的值等于( )21·cn·jy·com
A. B. C. D.
4.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )www.21-cn-jy.com
A.110° B.120° C.125° D.135°
5.已知如图,直线a⊥c,b⊥c,∠1=140°,那么∠2的度数是( )
A.40° B.50° C.60° D.140°
6.直角三角板和直尺如图所示放置,若∠1=36°,则∠2的度数为( )
A.34° B.44° C.54° D.64°
7.如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°,∠1=35,∠2=25°,则∠B的度数为( )www-2-1-cnjy-com
A.20° B.25° C.30° D.35°
8.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A.30° B.40° C.50° D.60°
9.如图,AB∥CD,若∠2=125°,则∠1的度数是( )
A.55° B.65° C.75° D.85°
10.如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( )
A.∠1+∠2=∠3 B.∠1=∠2>∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3的大小没有关系
11.如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )21*cnjy*com
A.5 B.6 C.7 D.8
12.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
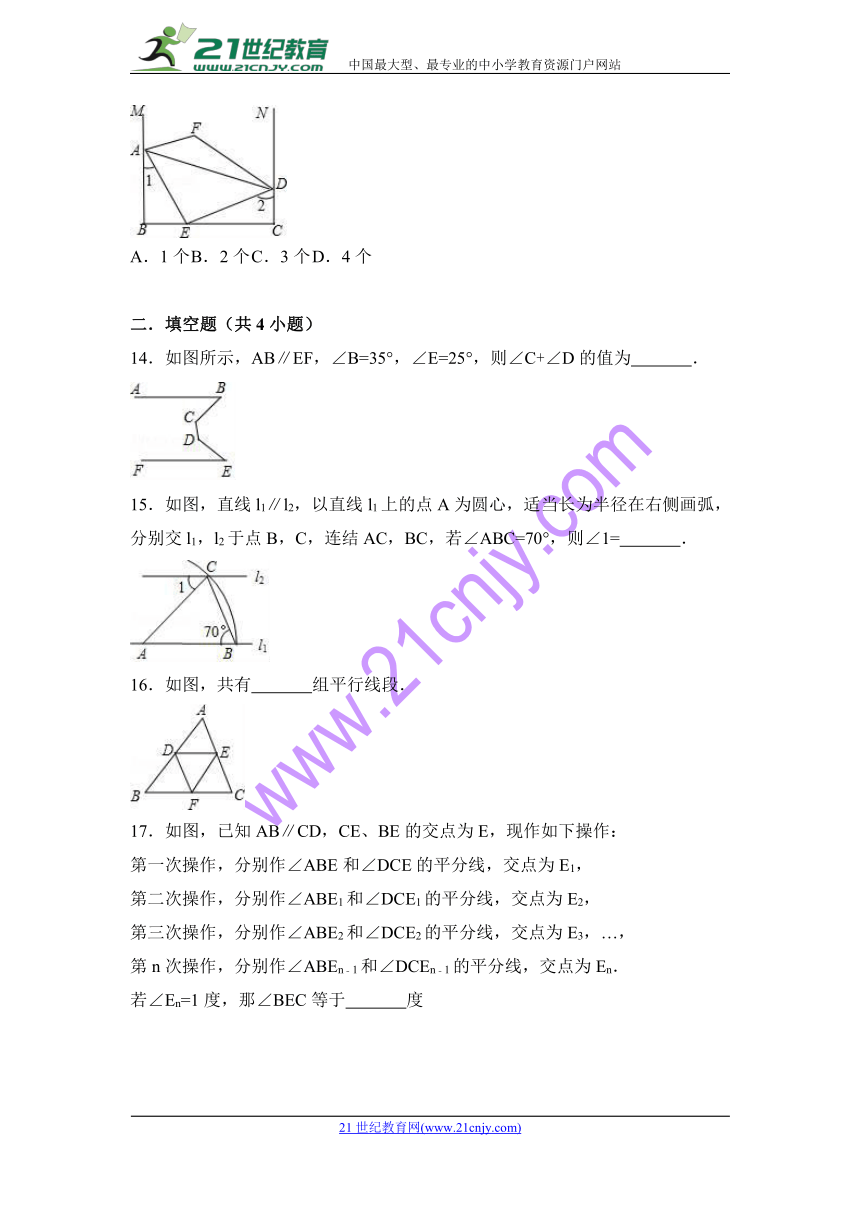
13.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:
①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共4小题)
14.如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为 .
15.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径在右侧画弧,分别交l1,l2于点B,C,连结AC,BC,若∠ABC=70°,则∠1= .
16.如图,共有 组平行线段.
17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度
三.解答题(共7小题)
18.如图,AB∥CD,EF平分∠AEG,若∠EGD=130°,求∠EFG的度数.
19.如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.【21cnj*y.co*m】
20.如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线( )
∴∠ABD=∠DBC( )
∵ED∥BC( )
∴∠BDE=∠DBC( )
∴ ( )
又∵∠FED=∠BDE( )
∴ ∥ ( )
∴∠AEF=∠ABD( )
∴∠AEF=∠DEF( )
∴EF是∠AED的平分线( )
21.如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
22.如图,BD⊥AC于D,EF⊥AC于F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
23.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.21-cnjy*com
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
24.如图1,直线m∥n,点B、F在直线m上,点E、C在直线n上,连结FE并延长至点A,连结BA和CA,使∠AEC=∠BAC.
(1)求证:∠BFA+∠BAC=180°;
(2)请在图1中找出与∠CAF相等的角,并加以证明;
(3)如图2,连结BC交AF于点D,作∠CBF和∠CEF的角平分线交于点M,若∠ADC=α,请直接写出∠M的度数(用含α的式子表示)
参考答案与试题解析
一.选择题(共13小题)
1.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【解答】解:已知直线a、b被直线c所截,那么∠1的同位角是∠2,
故选:A.
2.如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
A.35° B.40° C.45° D.55°
【解答】解:根据三角形外角性质,可得∠3=∠1+∠4,
∴∠4=∠3﹣∠1=95°﹣50°=45°,
∵a∥b,
∴∠2=∠4=45°.
故选:C.
3.如图,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,垂足为点M,PN∥OB,PN与OA相交于点N,那么的值等于( )
A. B. C. D.
【解答】解:如图,过点P作PE⊥OA于点E,
∵OP是∠AOB的平分线,
∴PE=PM,
∵PN∥OB,
∴∠POM=∠OPN,
∴∠PNE=∠PON+∠OPN=∠PON+∠POM=∠AOB=45°,
∴的值=.
故选:B.
4.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A.110° B.120° C.125° D.135°
【解答】解:如图所示,过E作EG∥AB,
∵AB∥CD,
∴EG∥CD,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠BED+∠CDE=360°,
又∵DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,
∴∠FBE+∠FDE=(∠ABE+∠CDE)=(360°﹣90°)=135°,
∴四边形BEDF中,∠BFD=360°﹣∠FBE﹣∠FDE﹣∠BED=360°﹣135°﹣90°=135°.21cnjy.com
故选:D.
5.已知如图,直线a⊥c,b⊥c,∠1=140°,那么∠2的度数是( )
A.40° B.50° C.60° D.140°
【解答】解:∵c⊥a,c⊥b,
∴∠α=∠β,
∴a∥b,
∴∠1=∠3,
∵∠2+∠3=180°,
∴∠2=180°﹣∠1=40°.
故选:A.
6.直角三角板和直尺如图所示放置,若∠1=36°,则∠2的度数为( )
A.34° B.44° C.54° D.64°
【解答】解:作直线AB∥a,
∵a∥b
∴AB∥a∥b,
∵AB∥a,
∴∠1=∠3,
∵AB∥b,
∴∠2=∠4,
∵∠3+∠4=90°,
∴∠1+∠2=90°,
∵∠1=36°,
∴∠2=90°﹣36°=54°,
故选:C.
7.如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°,∠1=35,∠2=25°,则∠B的度数为( )【21·世纪·教育·网】
A.20° B.25° C.30° D.35°
【解答】解:根据三角形外角性质,可得∠3=∠B+∠1,
∵直线a∥b,
∴∠3+∠ACD+∠2=180°,
∴∠B+∠1+∠ACD+∠2=180°,
又∵∠1=35,∠2=25°,
∴∠1+∠2=60°,
∴∠B+60°+90°=180°,
∴∠B=30°,
故选:C.
8.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A.30° B.40° C.50° D.60°
【解答】解:∵a∥b,∠1=60°,
∴∠3=∠1=60°,
∴∠2=90°﹣∠3=90°﹣60°=30°.
故选:A.
9.如图,AB∥CD,若∠2=125°,则∠1的度数是( )
A.55° B.65° C.75° D.85°
【解答】解:∵AB∥CD,
∴∠2=∠CAB,∠1=∠3,
∵∠CAB+∠3=180°,
∴∠1=180°﹣125°=55°,
故选:A.
10.如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( )
A.∠1+∠2=∠3 B.∠1=∠2>∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3的大小没有关系
【解答】解:∵AB∥CD,AD∥BC,
∴∠1=∠ACB,∠4=∠2,
∵∠CBE=∠4+∠ACB,
∴∠3=∠1+∠2,
∵∠1≠∠2且∠2<∠3,
故B,C,D错误,A正确,
故选:A.
11.如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )2-1-c-n-j-y
A.5 B.6 C.7 D.8
【解答】解:∵FM平分∠EFD,
∴∠EFM=∠DFM=∠CFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF=∠AEF,
∵EM平分∠BEF,
∴∠BEM=∠FEM=∠BEF,
∴∠GEF+∠FEM=(∠AEF+∠BEF)=90°,即∠GEM=90°,
∠FEM+∠EFM=(∠BEF+∠CFE),
∵AB∥CD,
∴∠EGF=∠AEG,∠CFE=∠AEF
∴∠FEM+∠EFM=(∠BEF+∠CFE)=(BEF+∠AEF)=90°,
∴在△EMF中,∠EMF=90°,
∴∠GEM=∠EMF,
∴EG∥FM,
∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.【21教育名师】
故选:C.
12.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【解答】解:点E有4种可能位置.
(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β﹣α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)如图,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α﹣β.
(4)如图,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°﹣α﹣β.
∴∠AEC的度数可能为β﹣α,α+β,α﹣β,360°﹣α﹣β.
故选:D.
13.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:21教育网
①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
故选:C.
二.填空题(共4小题)
14.如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为 240° .
【解答】解:如图所示,过C作CG∥AB,过D作DH∥EF,
∵AB∥EF,
∴AB∥EF∥CG∥DH,
∴∠1=∠B=35°,∠2=∠E=25°,∠GCD+∠HDC=180°,
∴∠BCD+∠CDE=35°+180°+25°=240°,
故答案为:240°.
15.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径在右侧画弧,分别交l1,l2于点B,C,连结AC,BC,若∠ABC=70°,则∠1= 40° .
【解答】解:根据题意得:AB=AC,
∴∠ACB=∠ABC=70°,
∵直线l1∥l2,
∴∠1+∠ACB+∠ABC=180°,
∴∠1=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°.
故答案为:40°.
16.如图,共有 9 组平行线段.
【解答】解:图中的平行线段有AD∥EF;BD∥EF;DE∥FB;DE∥FC;DF∥AE;DF∥EC;DE∥BC;DF∥AC;EF∥AB.共有9对.21世纪教育网
故答案为:9.
17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 2n 度
【解答】解:如图①,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图②,∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;
如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;
…
以此类推,∠En=∠BEC.
∴当∠En=1度时,∠BEC等于2n度.
故答案为:2n .
三.解答题(共7小题)
18.如图,AB∥CD,EF平分∠AEG,若∠EGD=130°,求∠EFG的度数.
【解答】解:∵AB∥CD,
∴∠AEG=∠EGD=130°,
∵EF平分∠AEG,
∴∠AEF=∠AEG=65°,
∵AB∥CD,
∴∠EFG=∠AEF=65°.
19.如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.21*教*育*名*师
【解答】解:∵OF平分∠COE,
∴∠EOF=∠FOC=17°,
∴∠EOC=34°,
∴∠BOD=34°,
∵OA⊥BC,
∴∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+34°=124°.
20.如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线( 已知 )
∴∠ABD=∠DBC( 角平分线定义 )
∵ED∥BC( 已知 )
∴∠BDE=∠DBC( 两直线平行,内错角相等 )
∴ ∠ABD=∠BDE ( 等量代换 )
又∵∠FED=∠BDE( 已知 )
∴ EF ∥ BD ( 内错角相等,两直线平行 )
∴∠AEF=∠ABD( 两直线平行,同位角相等 )
∴∠AEF=∠DEF( 等量代换 )
∴EF是∠AED的平分线( 角平分线定义 )
【解答】证明:∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线定义);
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠BDE(等量代换);
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行),
∴∠AEF=∠ABD(两直线平行,同位角相等),
∴∠AEF=∠DEF(等量代换),
∴EF是∠AED的平分线(角平分线定义).
21.如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 4 .
【解答】解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD、CE即为所求;
(3)△BCD的面积为×4×4﹣×1×3﹣×1×3﹣1=4,
故答案为:4
22.如图,BD⊥AC于D,EF⊥AC于F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
【解答】解:(1)∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠EFG=∠1=35°,
∴∠GFC=90°+35°=125°;
(2)∵BD∥EF,
∴∠2=∠CBD,
∴∠1=∠CBD,
∴GF∥BC,
∵∠AMD=∠AGF,
∴MD∥GF,
∴DM∥BC.
23.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.2·1·c·n·j·y
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
【解答】解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,
即9t+30°﹣3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,
即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=∠BOD,
即9t﹣60°﹣3t=(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=∠BOD,
即3t﹣(9t﹣240°)=(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
24.如图1,直线m∥n,点B、F在直线m上,点E、C在直线n上,连结FE并延长至点A,连结BA和CA,使∠AEC=∠BAC.21·世纪*教育网
(1)求证:∠BFA+∠BAC=180°;
(2)请在图1中找出与∠CAF相等的角,并加以证明;
(3)如图2,连结BC交AF于点D,作∠CBF和∠CEF的角平分线交于点M,若∠ADC=α,请直接写出∠M的度数(用含α的式子表示)【21教育】
【解答】解:(1)如图1,∵直线m∥n,
∴∠AEC=∠AFM,
∵∠AEC=∠BAC,
∴∠AFM=∠BAC,
又∵∠BFA+∠AFM=180°,
∴∠BFA+∠BAC=180°;
(2)与∠CAF相等的角有:∠ANC,∠ABF,∠BNG.
证明:∵∠AEC=∠BAC,∠ACE=∠NCA,
∴∠CAE=∠ANC=∠BNG,
∵m∥n,
∴∠ABF=∠ANC,
∴与∠CAF相等的角有:∠ANC,∠ABF,∠BNG;
(3)如图2,过D作DH∥BF,过M作MG∥BF,
∵BF∥CE,
∴DH∥BF∥CE,MG∥BF∥CE,
∴∠CED=∠HDE,∠FBD=∠HDB,
∴∠CED+∠FBD=∠EDB=180°﹣∠ADC=180°﹣α,
∵∠CBF和∠CEF的角平分线交于点M,
∴∠CEM+∠FBM=(∠CED+∠FBD)=(180°﹣α)=90°﹣α,
∵MG∥BF∥CE,
∴∠CEM=∠GME,∠FBM=∠GMB,
∴∠BME=∠GME+∠GMB=∠CEM+∠FBM=90°﹣α.
一.选择题(共13小题)
1.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
2.如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
A.35° B.40° C.45° D.55°
3.如图,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,垂足为点M,PN∥OB,PN与OA相交于点N,那么的值等于( )21·cn·jy·com
A. B. C. D.
4.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )www.21-cn-jy.com
A.110° B.120° C.125° D.135°
5.已知如图,直线a⊥c,b⊥c,∠1=140°,那么∠2的度数是( )
A.40° B.50° C.60° D.140°
6.直角三角板和直尺如图所示放置,若∠1=36°,则∠2的度数为( )
A.34° B.44° C.54° D.64°
7.如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°,∠1=35,∠2=25°,则∠B的度数为( )www-2-1-cnjy-com
A.20° B.25° C.30° D.35°
8.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A.30° B.40° C.50° D.60°
9.如图,AB∥CD,若∠2=125°,则∠1的度数是( )
A.55° B.65° C.75° D.85°
10.如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( )
A.∠1+∠2=∠3 B.∠1=∠2>∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3的大小没有关系
11.如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )21*cnjy*com
A.5 B.6 C.7 D.8
12.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
13.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:
①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共4小题)
14.如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为 .
15.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径在右侧画弧,分别交l1,l2于点B,C,连结AC,BC,若∠ABC=70°,则∠1= .
16.如图,共有 组平行线段.
17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度
三.解答题(共7小题)
18.如图,AB∥CD,EF平分∠AEG,若∠EGD=130°,求∠EFG的度数.
19.如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.【21cnj*y.co*m】
20.如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线( )
∴∠ABD=∠DBC( )
∵ED∥BC( )
∴∠BDE=∠DBC( )
∴ ( )
又∵∠FED=∠BDE( )
∴ ∥ ( )
∴∠AEF=∠ABD( )
∴∠AEF=∠DEF( )
∴EF是∠AED的平分线( )
21.如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 .
22.如图,BD⊥AC于D,EF⊥AC于F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
23.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.21-cnjy*com
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
24.如图1,直线m∥n,点B、F在直线m上,点E、C在直线n上,连结FE并延长至点A,连结BA和CA,使∠AEC=∠BAC.
(1)求证:∠BFA+∠BAC=180°;
(2)请在图1中找出与∠CAF相等的角,并加以证明;
(3)如图2,连结BC交AF于点D,作∠CBF和∠CEF的角平分线交于点M,若∠ADC=α,请直接写出∠M的度数(用含α的式子表示)
参考答案与试题解析
一.选择题(共13小题)
1.如图,已知直线a、b被直线c所截,那么∠1的同位角是( )
A.∠2 B.∠3 C.∠4 D.∠5
【解答】解:已知直线a、b被直线c所截,那么∠1的同位角是∠2,
故选:A.
2.如图,直线a∥b,若∠1=50°,∠3=95°,则∠2的度数为( )
A.35° B.40° C.45° D.55°
【解答】解:根据三角形外角性质,可得∠3=∠1+∠4,
∴∠4=∠3﹣∠1=95°﹣50°=45°,
∵a∥b,
∴∠2=∠4=45°.
故选:C.
3.如图,∠AOB=45°,OC是∠AOB的角平分线,PM⊥OB,垂足为点M,PN∥OB,PN与OA相交于点N,那么的值等于( )
A. B. C. D.
【解答】解:如图,过点P作PE⊥OA于点E,
∵OP是∠AOB的平分线,
∴PE=PM,
∵PN∥OB,
∴∠POM=∠OPN,
∴∠PNE=∠PON+∠OPN=∠PON+∠POM=∠AOB=45°,
∴的值=.
故选:B.
4.如图,AB∥CD,DE⊥BE,BF、DF分别为∠ABE、∠CDE的角平分线,则∠BFD=( )
A.110° B.120° C.125° D.135°
【解答】解:如图所示,过E作EG∥AB,
∵AB∥CD,
∴EG∥CD,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠BED+∠CDE=360°,
又∵DE⊥BE,BF,DF分别为∠ABE,∠CDE的角平分线,
∴∠FBE+∠FDE=(∠ABE+∠CDE)=(360°﹣90°)=135°,
∴四边形BEDF中,∠BFD=360°﹣∠FBE﹣∠FDE﹣∠BED=360°﹣135°﹣90°=135°.21cnjy.com
故选:D.
5.已知如图,直线a⊥c,b⊥c,∠1=140°,那么∠2的度数是( )
A.40° B.50° C.60° D.140°
【解答】解:∵c⊥a,c⊥b,
∴∠α=∠β,
∴a∥b,
∴∠1=∠3,
∵∠2+∠3=180°,
∴∠2=180°﹣∠1=40°.
故选:A.
6.直角三角板和直尺如图所示放置,若∠1=36°,则∠2的度数为( )
A.34° B.44° C.54° D.64°
【解答】解:作直线AB∥a,
∵a∥b
∴AB∥a∥b,
∵AB∥a,
∴∠1=∠3,
∵AB∥b,
∴∠2=∠4,
∵∠3+∠4=90°,
∴∠1+∠2=90°,
∵∠1=36°,
∴∠2=90°﹣36°=54°,
故选:C.
7.如图,直线a∥b,Rt△BCD如图放置,∠DCB=90°,∠1=35,∠2=25°,则∠B的度数为( )【21·世纪·教育·网】
A.20° B.25° C.30° D.35°
【解答】解:根据三角形外角性质,可得∠3=∠B+∠1,
∵直线a∥b,
∴∠3+∠ACD+∠2=180°,
∴∠B+∠1+∠ACD+∠2=180°,
又∵∠1=35,∠2=25°,
∴∠1+∠2=60°,
∴∠B+60°+90°=180°,
∴∠B=30°,
故选:C.
8.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A.30° B.40° C.50° D.60°
【解答】解:∵a∥b,∠1=60°,
∴∠3=∠1=60°,
∴∠2=90°﹣∠3=90°﹣60°=30°.
故选:A.
9.如图,AB∥CD,若∠2=125°,则∠1的度数是( )
A.55° B.65° C.75° D.85°
【解答】解:∵AB∥CD,
∴∠2=∠CAB,∠1=∠3,
∵∠CAB+∠3=180°,
∴∠1=180°﹣125°=55°,
故选:A.
10.如图,已知AB∥CD,AD∥BC,∠ABE是平角,则下列说法中正确的是( )
A.∠1+∠2=∠3 B.∠1=∠2>∠3
C.∠1+∠2<∠3 D.∠1+∠2与∠3的大小没有关系
【解答】解:∵AB∥CD,AD∥BC,
∴∠1=∠ACB,∠4=∠2,
∵∠CBE=∠4+∠ACB,
∴∠3=∠1+∠2,
∵∠1≠∠2且∠2<∠3,
故B,C,D错误,A正确,
故选:A.
11.如图,AB∥CD,EG、EM、FM分别平分∠AEF,∠BEF,∠EFD,则图中与∠DFM相等的角(不含它本身)的个数为( )2-1-c-n-j-y
A.5 B.6 C.7 D.8
【解答】解:∵FM平分∠EFD,
∴∠EFM=∠DFM=∠CFE,
∵EG平分∠AEF,
∴∠AEG=∠GEF=∠AEF,
∵EM平分∠BEF,
∴∠BEM=∠FEM=∠BEF,
∴∠GEF+∠FEM=(∠AEF+∠BEF)=90°,即∠GEM=90°,
∠FEM+∠EFM=(∠BEF+∠CFE),
∵AB∥CD,
∴∠EGF=∠AEG,∠CFE=∠AEF
∴∠FEM+∠EFM=(∠BEF+∠CFE)=(BEF+∠AEF)=90°,
∴在△EMF中,∠EMF=90°,
∴∠GEM=∠EMF,
∴EG∥FM,
∴与∠DFM相等的角有:∠EFM、∠GEF、∠EGF、∠AEG以及∠GEF、∠EGF、∠AEG三个角的对顶角.【21教育名师】
故选:C.
12.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A.①②③ B.①②④ C.①③④ D.①②③④
【解答】解:点E有4种可能位置.
(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β﹣α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)如图,由AB∥CD,可得∠BOE3=∠DCE3=β,
∵∠BAE3=∠BOE3+∠AE3C,
∴∠AE3C=α﹣β.
(4)如图,由AB∥CD,可得∠BAE4+∠AE4C+∠DCE4=360°,
∴∠AE4C=360°﹣α﹣β.
∴∠AEC的度数可能为β﹣α,α+β,α﹣β,360°﹣α﹣β.
故选:D.
13.如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M,N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F.下列结论:21教育网
①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值
其中结论正确的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:∵AB⊥BC,AE⊥DE,
∴∠1+∠AEB=90°,∠DEC+∠AEB=90°,
∴∠1=∠DEC,
又∵∠1+∠2=90°,
∴∠DEC+∠2=90°,
∴∠C=90°,
∴∠B+∠C=180°,
∴AB∥CD,故①正确;
∴∠ADN=∠BAD,
∵∠ADC+∠ADN=180°,
∴∠BAD+∠ADC=180°,
又∵∠AEB≠∠BAD,
∴AEB+∠ADC≠180°,故②错误;
∵∠4+∠3=90°,∠2+∠1=90°,而∠3=∠1,
∴∠2=∠4,
∴ED平分∠ADC,故③正确;
∵∠1+∠2=90°,
∴∠EAM+∠EDN=360°﹣90°=270°.
∵∠EAM和∠EDN的平分线交于点F,
∴∠EAF+∠EDF=×270°=135°.
∵AE⊥DE,
∴∠3+∠4=90°,
∴∠FAD+∠FDA=135°﹣90°=45°,
∴∠F=180°﹣(∠FAD+∠FDA)=180﹣45°=135°,故④正确.
故选:C.
二.填空题(共4小题)
14.如图所示,AB∥EF,∠B=35°,∠E=25°,则∠C+∠D的值为 240° .
【解答】解:如图所示,过C作CG∥AB,过D作DH∥EF,
∵AB∥EF,
∴AB∥EF∥CG∥DH,
∴∠1=∠B=35°,∠2=∠E=25°,∠GCD+∠HDC=180°,
∴∠BCD+∠CDE=35°+180°+25°=240°,
故答案为:240°.
15.如图,直线l1∥l2,以直线l1上的点A为圆心,适当长为半径在右侧画弧,分别交l1,l2于点B,C,连结AC,BC,若∠ABC=70°,则∠1= 40° .
【解答】解:根据题意得:AB=AC,
∴∠ACB=∠ABC=70°,
∵直线l1∥l2,
∴∠1+∠ACB+∠ABC=180°,
∴∠1=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣70°=40°.
故答案为:40°.
16.如图,共有 9 组平行线段.
【解答】解:图中的平行线段有AD∥EF;BD∥EF;DE∥FB;DE∥FC;DF∥AE;DF∥EC;DE∥BC;DF∥AC;EF∥AB.共有9对.21世纪教育网
故答案为:9.
17.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 2n 度
【解答】解:如图①,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图②,∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;
如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;
…
以此类推,∠En=∠BEC.
∴当∠En=1度时,∠BEC等于2n度.
故答案为:2n .
三.解答题(共7小题)
18.如图,AB∥CD,EF平分∠AEG,若∠EGD=130°,求∠EFG的度数.
【解答】解:∵AB∥CD,
∴∠AEG=∠EGD=130°,
∵EF平分∠AEG,
∴∠AEF=∠AEG=65°,
∵AB∥CD,
∴∠EFG=∠AEF=65°.
19.如图,已知直线BC、DE交于O点,OA、OF为射线,OA⊥BC,OF平分∠COE,∠COF=17°.求∠AOD的度数.21*教*育*名*师
【解答】解:∵OF平分∠COE,
∴∠EOF=∠FOC=17°,
∴∠EOC=34°,
∴∠BOD=34°,
∵OA⊥BC,
∴∠AOB=90°,
∴∠AOD=∠AOB+∠BOD=90°+34°=124°.
20.如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线.完成下列推理过程:
证明:∵BD是∠ABC的平分线( 已知 )
∴∠ABD=∠DBC( 角平分线定义 )
∵ED∥BC( 已知 )
∴∠BDE=∠DBC( 两直线平行,内错角相等 )
∴ ∠ABD=∠BDE ( 等量代换 )
又∵∠FED=∠BDE( 已知 )
∴ EF ∥ BD ( 内错角相等,两直线平行 )
∴∠AEF=∠ABD( 两直线平行,同位角相等 )
∴∠AEF=∠DEF( 等量代换 )
∴EF是∠AED的平分线( 角平分线定义 )
【解答】证明:∵BD是∠ABC的平分线(已知),
∴∠ABD=∠DBC(角平分线定义);
∵ED∥BC(已知),
∴∠BDE=∠DBC(两直线平行,内错角相等),
∴∠ABD=∠BDE(等量代换);
又∵∠FED=∠BDE(已知),
∴EF∥BD(内错角相等,两直线平行),
∴∠AEF=∠ABD(两直线平行,同位角相等),
∴∠AEF=∠DEF(等量代换),
∴EF是∠AED的平分线(角平分线定义).
21.如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)画出AB边上的中线CD和高线CE;(利用网格点和直尺画图)
(3)△BCD的面积为 4 .
【解答】解:(1)如图所示,△A′B′C′即为所求;
(2)如图所示,CD、CE即为所求;
(3)△BCD的面积为×4×4﹣×1×3﹣×1×3﹣1=4,
故答案为:4
22.如图,BD⊥AC于D,EF⊥AC于F,∠AMD=∠AGF,∠1=∠2=35°.
(1)求∠GFC的度数;
(2)求证:DM∥BC.
【解答】解:(1)∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠EFG=∠1=35°,
∴∠GFC=90°+35°=125°;
(2)∵BD∥EF,
∴∠2=∠CBD,
∴∠1=∠CBD,
∴GF∥BC,
∵∠AMD=∠AGF,
∴MD∥GF,
∴DM∥BC.
23.如图,直线CD与EF相交于点O,∠COE=60°,将一直角三角尺AOB的直角顶点与O重合,OA平分∠COE.2·1·c·n·j·y
(1)求∠BOD的度数;
(2)将三角尺AOB以每秒3°的速度绕点O顺时针旋转,同时直线EF也以每秒9°的速度绕点O顺时针旋转,设运动时间为t秒(0≤t≤40).
①当t为何值时,直线EF平分∠AOB;
②若直线EF平分∠BOD,直接写出t的值.
【解答】解:(1)∵∠COE=60°,OA平分∠COE,
∴∠AOC=30°,
又∵∠AOB=90°,
∴∠BOD=180°﹣30°﹣90°=60°;
(2)①分两种情况:
当OE平分∠AOB时,∠AOE=45°,
即9t+30°﹣3t=45°,
解得t=2.5;
当OF平分∠AOB时,AOF=45°,
即9t﹣150°﹣3t=45°,
解得t=32.5;
综上所述,当t=2.5s或32.5s时,直线EF平分∠AOB;
②t的值为12s或36s.
分两种情况:
当OE平分∠BOD时,∠BOE=∠BOD,
即9t﹣60°﹣3t=(60°﹣3t),
解得t=12;
当OF平分∠BOD时,∠DOF=∠BOD,
即3t﹣(9t﹣240°)=(3t﹣60°),
解得t=36;
综上所述,若直线EF平分∠BOD,t的值为12s或36s.
24.如图1,直线m∥n,点B、F在直线m上,点E、C在直线n上,连结FE并延长至点A,连结BA和CA,使∠AEC=∠BAC.21·世纪*教育网
(1)求证:∠BFA+∠BAC=180°;
(2)请在图1中找出与∠CAF相等的角,并加以证明;
(3)如图2,连结BC交AF于点D,作∠CBF和∠CEF的角平分线交于点M,若∠ADC=α,请直接写出∠M的度数(用含α的式子表示)【21教育】
【解答】解:(1)如图1,∵直线m∥n,
∴∠AEC=∠AFM,
∵∠AEC=∠BAC,
∴∠AFM=∠BAC,
又∵∠BFA+∠AFM=180°,
∴∠BFA+∠BAC=180°;
(2)与∠CAF相等的角有:∠ANC,∠ABF,∠BNG.
证明:∵∠AEC=∠BAC,∠ACE=∠NCA,
∴∠CAE=∠ANC=∠BNG,
∵m∥n,
∴∠ABF=∠ANC,
∴与∠CAF相等的角有:∠ANC,∠ABF,∠BNG;
(3)如图2,过D作DH∥BF,过M作MG∥BF,
∵BF∥CE,
∴DH∥BF∥CE,MG∥BF∥CE,
∴∠CED=∠HDE,∠FBD=∠HDB,
∴∠CED+∠FBD=∠EDB=180°﹣∠ADC=180°﹣α,
∵∠CBF和∠CEF的角平分线交于点M,
∴∠CEM+∠FBM=(∠CED+∠FBD)=(180°﹣α)=90°﹣α,
∵MG∥BF∥CE,
∴∠CEM=∠GME,∠FBM=∠GMB,
∴∠BME=∠GME+∠GMB=∠CEM+∠FBM=90°﹣α.
