数学六年级下人教版4反比例课件 (共20张)
文档属性
| 名称 | 数学六年级下人教版4反比例课件 (共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 988.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-05 18:42:25 | ||
图片预览





文档简介
(共20张PPT)
第四单元 比例
4.2 反比例
教材第47~51页
课题引入
小游戏:西岔沟的李爷爷捡自己果园里最大的苹果摘了30个,准备分给
幼儿园的小朋友,老师说出小朋友的人数,请同学们回答分得
的苹果个数。
小朋友数 1 2 3 4 5 ……
每个小朋友的个数 30 15 10 7.5 6 ……
从这个表中,你有什么发现?小朋友的人数与每个小朋友分得的苹果个数成正比例吗?为什么?
教学新知
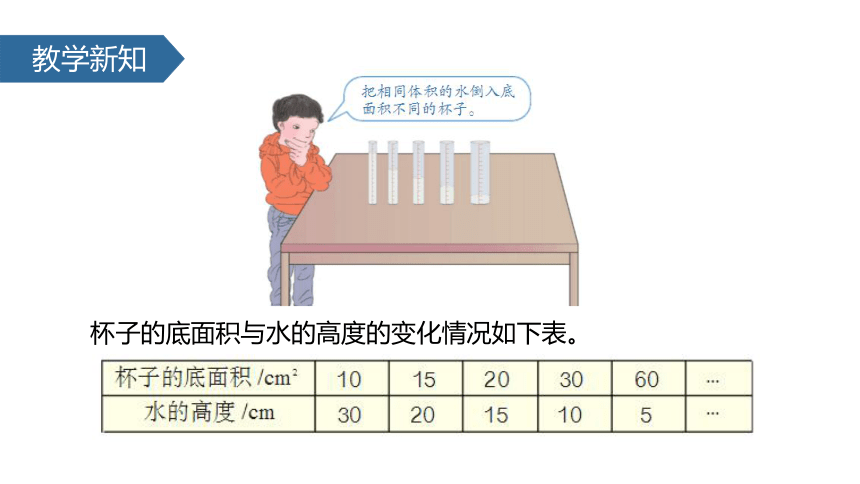
杯子的底面积与水的高度的变化情况如下表。
教学新知
观察上表回答下面的问题:
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。
例如:30×10=20×15=15×20=...=300
教学新知
积300,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
知识要点
在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
xy
教学新知
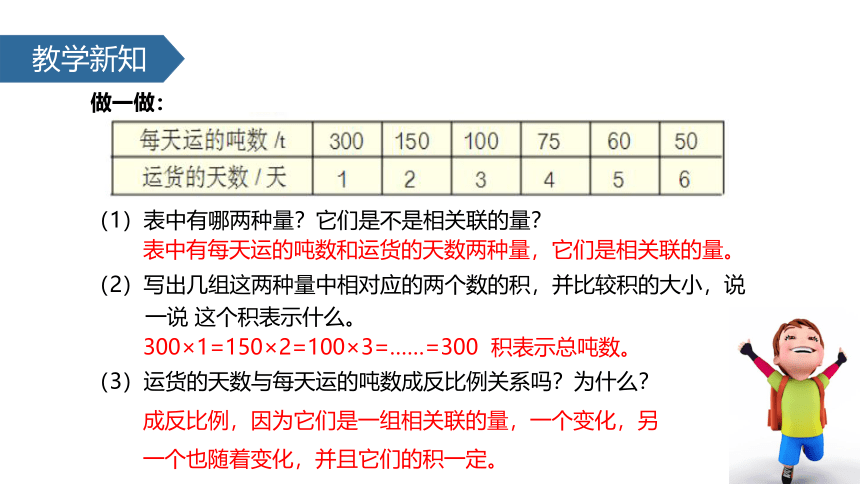
做一做:
(1)表中有哪两种量?它们是不是相关联的量?
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说
一说 这个积表示什么。
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
表中有每天运的吨数和运货的天数两种量,它们是相关联的量。
300×1=150×2=100×3=……=300 积表示总吨数。
成反比例,因为它们是一组相关联的量,一个变化,另
一个也随着变化,并且它们的积一定。
教学新知
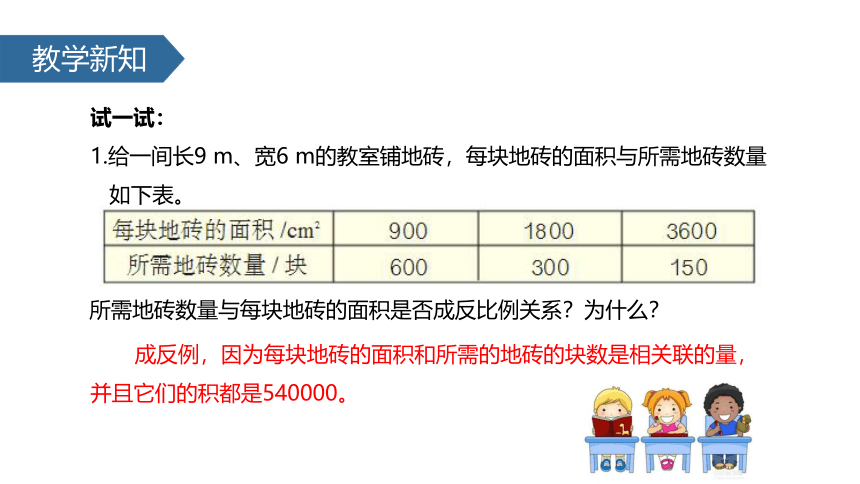
试一试:
1.给一间长9 m、宽6 m的教室铺地砖,每块地砖的面积与所需地砖数量
如下表。
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
成反例,因为每块地砖的面积和所需的地砖的块数是相关联的量,并且它们的积都是540000。
教学新知
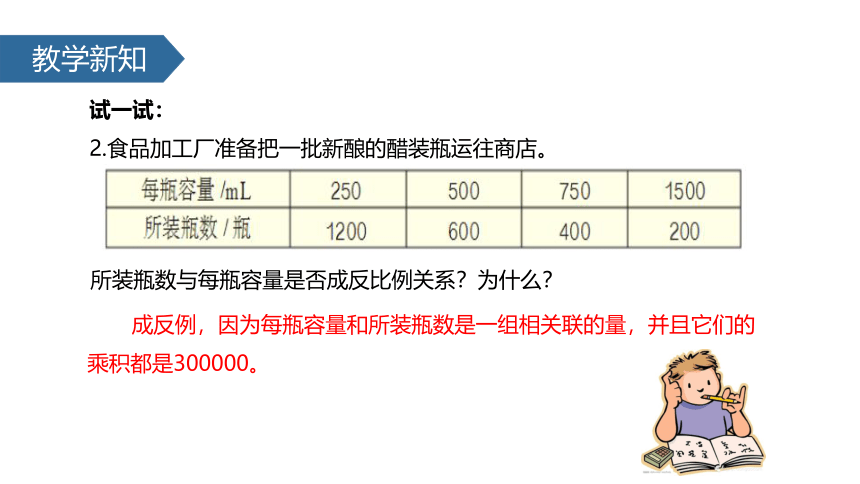
试一试:
2.食品加工厂准备把一批新酿的醋装瓶运往商店。
所装瓶数与每瓶容量是否成反比例关系?为什么?
成反例,因为每瓶容量和所装瓶数是一组相关联的量,并且它们的乘积都是300000。
教学新知
例一:长方体的体积一定,长方体的底面积和高成反比例吗?说说理由。
【解析】判断两个量是否成反比例,要看这两个量是否关联,要看两个量的变化是否相反,还要看两个量的乘积是否相等。长方体的体积=底面积×高,题中告诉了体积一定,而底面积和高又是一组相关联的量,是乘积的关系,所以底面积和高成反比例。
【方法小结】判断两个量是否成反比例,要看两个量是不是积的关系,并且积是不是一定的。
教学新知
例二:根据时间、路程和速度写出三个等量关系式,并说一说在什么条
件下相关联的两个量成什么比例。
【解析】根题意可以写出三个等量关系式,即:时间=路程÷速度、速度=路程÷时间、路程=速度×时间。在时间=路程÷速度中,如果时间一定,则路程和速度成正比例;在速度=路程÷时间中,如果速度一定,则路程和时间成正比例;在路程=速度×时间中,如果路程一定,速度和时间成反比例。
课堂练习
1.A、B 、C 三种量的关系是: A×B = C
(3)如果 A一定,那么 B和 C成( )比例;
(4)如果 B一定,那么 A和C 成( )比例;
(3)如果 C一定,那么 A和 B成( )比例。
2.判断
(1)一个因数不变,积与另一个因数成正比例。 ( )
(2)长方形的长一定,宽和面积成正比例。 ( )
(3)大米的总量一定,吃掉的和剩下的成反比例。 ( )
(4)圆的半径和周长成正比例。 ( )
正
正
反
√
√
×
√
课堂练习
(5)分数的分子一定,分数值和分母成反比例。 ( )
(6)铺地面积一定,方砖的边长和所需块数成反比例。( )
(7)铺地面积一定,方砖面积和所需块数成反比例。 ( )
(8)除数一定,被除数和商成正比例。 ( )
3.下表是李师傅加工一批零件时,每小时加工零件个数随时间变化的情
况。这两种量有什么关系
每小时加工零件的个数/个 20 30 40 60 ……
加工的时间/时 12 8 6 4 ……
×
√
√
√
每小时加工零件的个数和加工的时间是成反比例的量,它们之间的关系是反比例关系。
课后习题
1.填空。
(1)两种( )的量,一种量变化,另一种量( ),如果
这两种量中( )的两个数的( )一定,这两种量就叫做
成正比例的量,它们的关系叫做( ),关系式是
( )。
(2)两种( )的量,一种量变化,另一种量( ),如果
这两种量中( )的两个数的( )一定,这两种量就叫做成
反比例的量,它们的关系叫做( ),关系式是
( )。
相关联
随着变化
相对应
比值
正比例关系
相关联
随着变化
相对应
积
反比例关系
xy=k(一定)
课后习题
2.判断题。
(1)圆的面积和圆的半径成正比例。 ( )
(2)圆的面积和圆的半径的平方成正比例。 ( )
(3)圆的面积和圆的周长的平方成正比例。 ( )
(4)正方形的面积和边长成正比例。 ( )
(5)正方形的周长和边长成正比例。 ( )
(6)长方形的面积一定时,长和宽成反比例。 ( )
(7)长方形的周长一定时,长和宽成反比例。 ( )
(8)三角形的面积一定时,底和高成反比例。 ( )
×
√
×
×
√
√
×
√
课后习题
(9)梯形的面积一定时,上底和下底的和与高成反比例。 ( )
(10)圆的周长和圆的半径成正比例。 ( )
3.选择题。
(1)把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量。( )
A 成正比例 B 成反比例 C 不成比例
(2)和一定,加数和另一个加数。( )
A 成正比例 B 成反比例 C 不成比例
√
√
B
C
课后习题
(3)在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成
正比例关系是( ),成反比例关系是( )。
A 汽车每次运货吨数一定,运货次数和运货总吨数。
B 汽车运货次数一定,每次运货的吨数和运货总吨数。
C 汽车运货总吨数一定,每次运货的吨数和运货的次数。
4.下列各题中的两种量是不是成比例,成什么比例,并说明理由。
(1)买相同的电脑,购买的电脑台数与总价
(2)每捆练习本的本数相同,练习本的总本数与捆数
A、B
C
成正比例,因为台数与总价是相关联的量,并且它们的比值是一定的。
成正比例,因为总数和捆数是一组相关联的量,并且它们的比值一定。
课后习题
4.下列各题中的两种量是不是成比例,成什么比例,并说明理由。
(3)总路程一定,已行的路程与未行的路程
(4)分数值一定,分数的分子与分母
(5)长方形的长一定,它的面积和宽
(6)长方体的体积一定,底面积和高
不能比例,因为已行的路程和未行的路是和差的关系。
成正比例,因为分数分子与分母是一组相关联的量,并且它们的比值一定。
成正比例,因为面积和宽是一组相关联的量,并且它们的比值一定。
成反比例,因为底面积和高是一组相关联的量,并且它们的积一定。
课后习题
5.地板砖的面积和用砖数如下表,根据要求填空。
地板砖的面积(平方米) 0.5 0.8 1 ……
用砖块数 400 250 200 ……
(1)表中( )和( )是相关联的量,( )
随着( )的变化而变化。
(2)表中第一组这两种量相对应的两个数的积是( ),第三组这
两种量相对应的两个数的积是( )。
(3)上面所求出的积所表示的的意义是( ),地板砖的面积和
砖的块数的( )是一定的,所以地板砖的面积和砖的块数
( )。
地板砖的面积
用砖块数
用砖块数
地板砖的面积
200
200
铺地面积
积
成反比例
课后习题
6.下面题里的数量成什么关系?你能列出式子表示数量之间的相等关系
吗?
(1)小红看一本儿童小说,每天看12页,10天可以看完;如果每天看
15页,8天可以看完。
(2)一种螺丝钉,20个重30克。一盒这样的螺丝钉是600克,一共有
400个。
成反比例,总页数=每天看的页数×天数
成正比例,每个螺丝钉的重量=总重量÷数量
第四单元 比例
4.2 反比例
教材第47~51页
课题引入
小游戏:西岔沟的李爷爷捡自己果园里最大的苹果摘了30个,准备分给
幼儿园的小朋友,老师说出小朋友的人数,请同学们回答分得
的苹果个数。
小朋友数 1 2 3 4 5 ……
每个小朋友的个数 30 15 10 7.5 6 ……
从这个表中,你有什么发现?小朋友的人数与每个小朋友分得的苹果个数成正比例吗?为什么?
教学新知
杯子的底面积与水的高度的变化情况如下表。
教学新知
观察上表回答下面的问题:
(1)表中有哪两种量?
(2)水的高度是怎样随着杯子底面积的大小变化而变化的?
(3)相对应的杯子的底面积与水的高度的乘积分别是多少?
从上表可以看出,水的高度和杯子的底面积是两种相关联的量,水的高度是随着杯子的底面积的变大而不断变小的,而且水的高度与杯子的底面积的乘积总是一定的。
例如:30×10=20×15=15×20=...=300
教学新知
积300,实际就是倒入杯子的水的体积。用式子表示它们的关系就是:
像这样,两种相关联的量,一种量变化,另一种量也随着变化,如果这两种量中相对应的两个数的乘积一定,这两种量就叫做成反比例的量,它们的关系叫做反比例关系。
知识要点
在上面的实验中,高度和底面积是成反比例的量,高度与底面积成反比例关系。
如果用字母x和y表示两种相关联的量,用k表示它们的积(一定),反比例关系可以用下面的式子表示:
xy
教学新知
做一做:
(1)表中有哪两种量?它们是不是相关联的量?
(2)写出几组这两种量中相对应的两个数的积,并比较积的大小,说
一说 这个积表示什么。
(3)运货的天数与每天运的吨数成反比例关系吗?为什么?
表中有每天运的吨数和运货的天数两种量,它们是相关联的量。
300×1=150×2=100×3=……=300 积表示总吨数。
成反比例,因为它们是一组相关联的量,一个变化,另
一个也随着变化,并且它们的积一定。
教学新知
试一试:
1.给一间长9 m、宽6 m的教室铺地砖,每块地砖的面积与所需地砖数量
如下表。
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
成反例,因为每块地砖的面积和所需的地砖的块数是相关联的量,并且它们的积都是540000。
教学新知
试一试:
2.食品加工厂准备把一批新酿的醋装瓶运往商店。
所装瓶数与每瓶容量是否成反比例关系?为什么?
成反例,因为每瓶容量和所装瓶数是一组相关联的量,并且它们的乘积都是300000。
教学新知
例一:长方体的体积一定,长方体的底面积和高成反比例吗?说说理由。
【解析】判断两个量是否成反比例,要看这两个量是否关联,要看两个量的变化是否相反,还要看两个量的乘积是否相等。长方体的体积=底面积×高,题中告诉了体积一定,而底面积和高又是一组相关联的量,是乘积的关系,所以底面积和高成反比例。
【方法小结】判断两个量是否成反比例,要看两个量是不是积的关系,并且积是不是一定的。
教学新知
例二:根据时间、路程和速度写出三个等量关系式,并说一说在什么条
件下相关联的两个量成什么比例。
【解析】根题意可以写出三个等量关系式,即:时间=路程÷速度、速度=路程÷时间、路程=速度×时间。在时间=路程÷速度中,如果时间一定,则路程和速度成正比例;在速度=路程÷时间中,如果速度一定,则路程和时间成正比例;在路程=速度×时间中,如果路程一定,速度和时间成反比例。
课堂练习
1.A、B 、C 三种量的关系是: A×B = C
(3)如果 A一定,那么 B和 C成( )比例;
(4)如果 B一定,那么 A和C 成( )比例;
(3)如果 C一定,那么 A和 B成( )比例。
2.判断
(1)一个因数不变,积与另一个因数成正比例。 ( )
(2)长方形的长一定,宽和面积成正比例。 ( )
(3)大米的总量一定,吃掉的和剩下的成反比例。 ( )
(4)圆的半径和周长成正比例。 ( )
正
正
反
√
√
×
√
课堂练习
(5)分数的分子一定,分数值和分母成反比例。 ( )
(6)铺地面积一定,方砖的边长和所需块数成反比例。( )
(7)铺地面积一定,方砖面积和所需块数成反比例。 ( )
(8)除数一定,被除数和商成正比例。 ( )
3.下表是李师傅加工一批零件时,每小时加工零件个数随时间变化的情
况。这两种量有什么关系
每小时加工零件的个数/个 20 30 40 60 ……
加工的时间/时 12 8 6 4 ……
×
√
√
√
每小时加工零件的个数和加工的时间是成反比例的量,它们之间的关系是反比例关系。
课后习题
1.填空。
(1)两种( )的量,一种量变化,另一种量( ),如果
这两种量中( )的两个数的( )一定,这两种量就叫做
成正比例的量,它们的关系叫做( ),关系式是
( )。
(2)两种( )的量,一种量变化,另一种量( ),如果
这两种量中( )的两个数的( )一定,这两种量就叫做成
反比例的量,它们的关系叫做( ),关系式是
( )。
相关联
随着变化
相对应
比值
正比例关系
相关联
随着变化
相对应
积
反比例关系
xy=k(一定)
课后习题
2.判断题。
(1)圆的面积和圆的半径成正比例。 ( )
(2)圆的面积和圆的半径的平方成正比例。 ( )
(3)圆的面积和圆的周长的平方成正比例。 ( )
(4)正方形的面积和边长成正比例。 ( )
(5)正方形的周长和边长成正比例。 ( )
(6)长方形的面积一定时,长和宽成反比例。 ( )
(7)长方形的周长一定时,长和宽成反比例。 ( )
(8)三角形的面积一定时,底和高成反比例。 ( )
×
√
×
×
√
√
×
√
课后习题
(9)梯形的面积一定时,上底和下底的和与高成反比例。 ( )
(10)圆的周长和圆的半径成正比例。 ( )
3.选择题。
(1)把一堆化肥装入麻袋,麻袋的数量和每袋化肥的重量。( )
A 成正比例 B 成反比例 C 不成比例
(2)和一定,加数和另一个加数。( )
A 成正比例 B 成反比例 C 不成比例
√
√
B
C
课后习题
(3)在汽车每次运货吨数,运货次数和运货的总吨数这三种量中,成
正比例关系是( ),成反比例关系是( )。
A 汽车每次运货吨数一定,运货次数和运货总吨数。
B 汽车运货次数一定,每次运货的吨数和运货总吨数。
C 汽车运货总吨数一定,每次运货的吨数和运货的次数。
4.下列各题中的两种量是不是成比例,成什么比例,并说明理由。
(1)买相同的电脑,购买的电脑台数与总价
(2)每捆练习本的本数相同,练习本的总本数与捆数
A、B
C
成正比例,因为台数与总价是相关联的量,并且它们的比值是一定的。
成正比例,因为总数和捆数是一组相关联的量,并且它们的比值一定。
课后习题
4.下列各题中的两种量是不是成比例,成什么比例,并说明理由。
(3)总路程一定,已行的路程与未行的路程
(4)分数值一定,分数的分子与分母
(5)长方形的长一定,它的面积和宽
(6)长方体的体积一定,底面积和高
不能比例,因为已行的路程和未行的路是和差的关系。
成正比例,因为分数分子与分母是一组相关联的量,并且它们的比值一定。
成正比例,因为面积和宽是一组相关联的量,并且它们的比值一定。
成反比例,因为底面积和高是一组相关联的量,并且它们的积一定。
课后习题
5.地板砖的面积和用砖数如下表,根据要求填空。
地板砖的面积(平方米) 0.5 0.8 1 ……
用砖块数 400 250 200 ……
(1)表中( )和( )是相关联的量,( )
随着( )的变化而变化。
(2)表中第一组这两种量相对应的两个数的积是( ),第三组这
两种量相对应的两个数的积是( )。
(3)上面所求出的积所表示的的意义是( ),地板砖的面积和
砖的块数的( )是一定的,所以地板砖的面积和砖的块数
( )。
地板砖的面积
用砖块数
用砖块数
地板砖的面积
200
200
铺地面积
积
成反比例
课后习题
6.下面题里的数量成什么关系?你能列出式子表示数量之间的相等关系
吗?
(1)小红看一本儿童小说,每天看12页,10天可以看完;如果每天看
15页,8天可以看完。
(2)一种螺丝钉,20个重30克。一盒这样的螺丝钉是600克,一共有
400个。
成反比例,总页数=每天看的页数×天数
成正比例,每个螺丝钉的重量=总重量÷数量
