2016-2017学年黑龙江省哈尔滨156中八年级(上)期中数学试卷(五四学制)(含解析)
文档属性
| 名称 | 2016-2017学年黑龙江省哈尔滨156中八年级(上)期中数学试卷(五四学制)(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 267.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-05 17:39:28 | ||
图片预览




文档简介
2016-2017学年黑龙江省哈尔滨156中八年级(上)期中数学试卷(五四学制)
一、选择题(每小题3分,共30分)
1.(3分)下列运算正确的是( )
A.x3+x3=2x6 B.x2?x4=x8 C.(xy)m=xym D.(﹣x5)4=x20
2.(3分)若(x+2)(x﹣3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=6 B.a=﹣1,b=6 C.a=5,b=﹣6 D.a=﹣1,b=﹣6
3.(3分)下列图形中,轴对称图形的个数是( )
A.1 B.2 C.3 D.4
4.(3分)若(x+y﹣3)2+(x﹣y+5)2=0.则x2﹣y2的值是( )
A.8 B.﹣8 C.15 D.﹣15
5.(3分)若(x﹣a)(x﹣5)的展开式中不含有x的一次项,则a的值为( )
A.0 B.5 C.﹣5 D.5或﹣5
6.(3分)到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线交点 B.三条角平分线交点
C.三条高的交点 D.三条边的垂直平分线交点
7.(3分)若x2﹣2(m﹣3)x+16是完全平方式,则m的值等于( )
A.﹣1 B.7 C.7或﹣7 D.7或﹣1
8.(3分)n个底边长为a,腰长为b的等腰△ABC拼成图,则图中的线段之和是( )
A.na+2nb B.na+nb+b C.na+2b D.2na+2b
9.(3分)下列说法中,正确的个数有( )
(1)关于某直线对称的两个三角形是全等三角形
(2)全等三角形是关于某直线对称的
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称
(5)轴对称图形的对应点所连线段被对称轴垂直平分
(6)等腰三角形的角平分线、中线、高线互相重合.
A.2 B.3 C.4 D.5
10.(3分)用四个完全一样的边长分别为a、b、c的直角三角板拼成图所示的图形,则下列结论中正确的是( )21教育网
A.c2=(a+b)2 B.c2=a2+2ab+b2 C.c2=a2﹣2ab+b2 D.c2=a2+b2
二、填空题(每小题3分,共30分)
11.(3分)计算: = .
12.(3分)若代数式2a2+3a+1的值为6,则代数式6a2+9a﹣5= .
13.(3分)设x﹣=1,则x2+= .
14.(3分)若x2+8x+18﹣2k=(x+4)2,则k= .
15.(3分)如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为 .www.21-cn-jy.com
16.(3分)已知x≠1,(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4,…【21教育名师】
观察上式,猜想计算:(1﹣2)(1+2+22+23+24+25)= .
17.(3分)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为 .【21教育】
18.(3分)如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于 .
19.(3分)如图,在三角形ABC中,AB=AC=BD,∠1=70°,则∠2的度数是 .
20.(3分)如图,在Rt△ABC,AC=BC,∠ACB=90°,AD是∠BAC的角平分线,若AD=8,则△ABD的面积为 .21-cnjy*com
三、解答题(共60分,其中22、24题各7分,21、23各8分,25--27题各10分)
21.(8分)计算:
(1)2(x2)3?x3﹣(3x3)3+(5x)2?x7
(2)(x4y+6x3y2﹣x2y3)÷(3x2y)
(3)(a+2b﹣3)(a﹣2b+3)
(4)简便计算:22016﹣22015.
22.(7分)先化简,再求值:(2x+1)2﹣(2x+1)(2x﹣1)+(x+1)(x﹣2)﹣x0,其中x=﹣1.
23.(8分)将下列各式分解因式
(1)9x3﹣25xy2
(2)﹣3x+6x2﹣3x3
(3)(x+y)2﹣(x﹣y)2
(4)x2﹣1+y2﹣2xy.
24.(7分)已知:如图,已知△ABC,
(1)分别画出与△ABC关于y轴对称的图形△A1B1C1
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
25.(10分)已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.求证:①BE=CD;②△AMN是等腰三角形.
26.(10分)为了援助失学儿童,初三学生李飞从2016年1月份开始,每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内.已知2月份存款后清点储蓄盒内有存款80元,5月份存款后清点储蓄盒内有存款125元.
(1)在李飞2016年1月份存款前,储蓄盒内已有存款多少元?
(2)为了实现2019年6月份存款后存款总数超过1000元的目标,李飞计划从2017年1月份开始,每月存款都比2016年每月存款多t元(t为整数),求t的最小值.
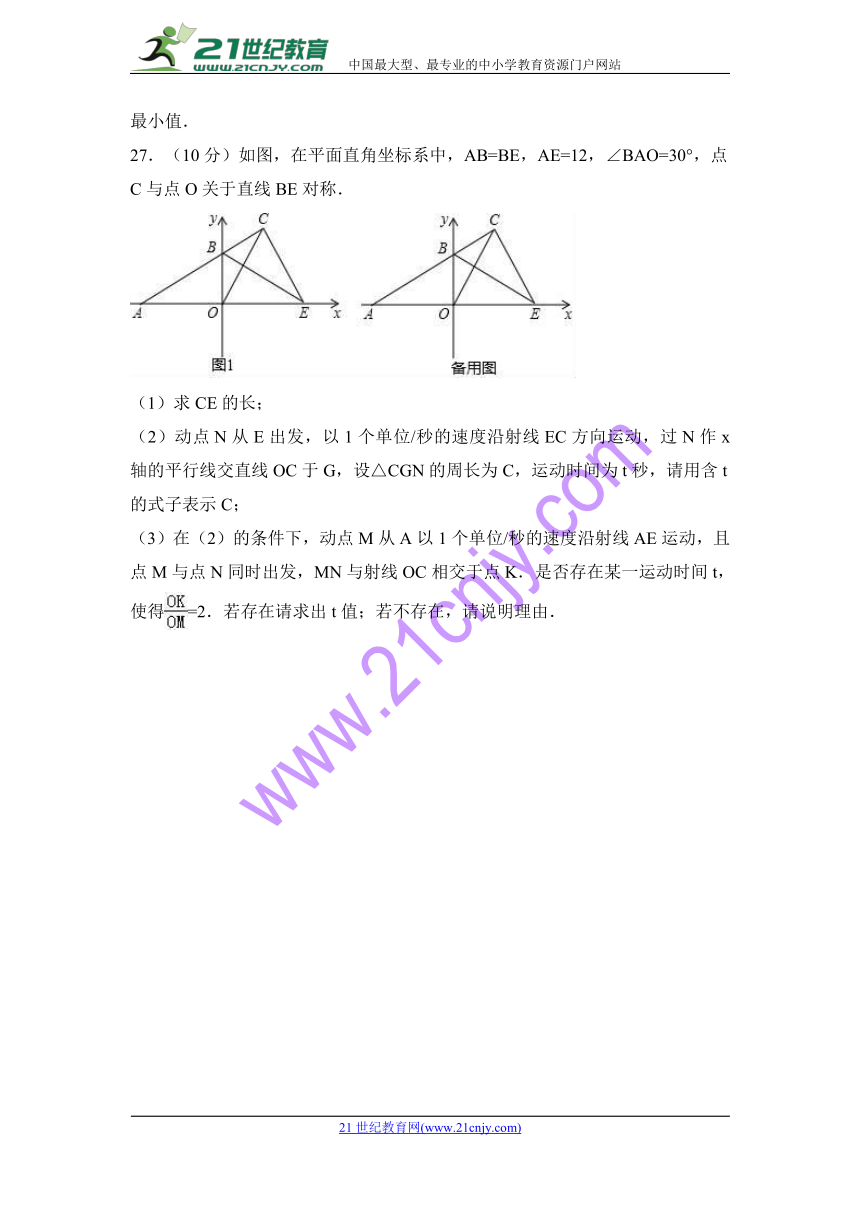
27.(10分)如图,在平面直角坐标系中,AB=BE,AE=12,∠BAO=30°,点C与点O关于直线BE对称.
(1)求CE的长;
(2)动点N从E出发,以1个单位/秒的速度沿射线EC方向运动,过N作x轴的平行线交直线OC于G,设△CGN的周长为C,运动时间为t秒,请用含t的式子表示C;
(3)在(2)的条件下,动点M从A以1个单位/秒的速度沿射线AE运动,且点M与点N同时出发,MN与射线OC相交于点K.是否存在某一运动时间t,使得=2.若存在请求出t值;若不存在,请说明理由.
2016-2017学年黑龙江省哈尔滨156中八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列运算正确的是( )
A.x3+x3=2x6 B.x2?x4=x8 C.(xy)m=xym D.(﹣x5)4=x20
【解答】解:A、x3+x3=2x3,故原题计算错误;
B、x2?x4=x6,故原题计算错误;
C、(xy)m=xmym,故原题计算错误;
D、(﹣x5)4=x20,故原题计算正确;
故选:D.
2.(3分)若(x+2)(x﹣3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=6 B.a=﹣1,b=6 C.a=5,b=﹣6 D.a=﹣1,b=﹣6
【解答】解:∵(x+2)(x﹣3)=x2﹣x﹣6=x2+ax+b,
∴a=﹣1,b=﹣6.
故选:D.
3.(3分)下列图形中,轴对称图形的个数是( )
A.1 B.2 C.3 D.4
【解答】解:中间两个图形是轴对称图形,轴对称图形的个数是2,故选B.
4.(3分)若(x+y﹣3)2+(x﹣y+5)2=0.则x2﹣y2的值是( )
A.8 B.﹣8 C.15 D.﹣15
【解答】解:∵(x+y﹣3)2+(x﹣y+5)2=0,
∴,
解得,
∴x2﹣y2=1﹣16=﹣15.
故选:D.
5.(3分)若(x﹣a)(x﹣5)的展开式中不含有x的一次项,则a的值为( )
A.0 B.5 C.﹣5 D.5或﹣5
【解答】解:(x﹣a)(x﹣5)
=x2﹣5x﹣ax+5a
=x2+(﹣5﹣a)x+5a,
∵(x﹣a)(x﹣5)的展开式中不含有x的一次项,
∴﹣5﹣a=0,
a=﹣5.
故选:C.
6.(3分)到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线交点 B.三条角平分线交点
C.三条高的交点 D.三条边的垂直平分线交点
【解答】解:∵到△ABC的三条边距离相等,
∴这点在这个三角形三条角平分线上,
即这点是三条角平分线的交点.
故选:B.
7.(3分)若x2﹣2(m﹣3)x+16是完全平方式,则m的值等于( )
A.﹣1 B.7 C.7或﹣7 D.7或﹣1
【解答】解:依题意,得m﹣3=±4,
解得m=7或﹣1.
故选:D.
8.(3分)n个底边长为a,腰长为b的等腰△ABC拼成图,则图中的线段之和是( )
A.na+2nb B.na+nb+b C.na+2b D.2na+2b
【解答】解:当有2个等腰三角形时,线段之和为:2a+3b
当有3个等腰三角形时,线段之和为:3a+4b
当有4个等腰三角形时,线段之和为:4a+5b
…
当有n个等腰三角形时,线段之和为:na+(n+1)b=na+nb+b
故选:B.
9.(3分)下列说法中,正确的个数有( )
(1)关于某直线对称的两个三角形是全等三角形
(2)全等三角形是关于某直线对称的
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称
(5)轴对称图形的对应点所连线段被对称轴垂直平分
(6)等腰三角形的角平分线、中线、高线互相重合.
A.2 B.3 C.4 D.5
【解答】解:(1)关于某直线对称的两个三角形是全等三角形,正确;
(2)全等三角形不一定关于某直线对称的,错误;
(3)两个图形关于某直线对称,则这两个图形不一定分别位于这条直线的两侧,错误;
(4)有一条公共边的两个全等三角形不一定关于公共边所在的直线对称,错误;
(5)轴对称图形的对应点所连线段被对称轴垂直平分,正确;
(6)等腰三角形的角平分线、中线、高线互相重合.正确;
故选:B.
10.(3分)用四个完全一样的边长分别为a、b、c的直角三角板拼成图所示的图形,则下列结论中正确的是( )21世纪教育网
A.c2=(a+b)2 B.c2=a2+2ab+b2 C.c2=a2﹣2ab+b2 D.c2=a2+b2
【解答】解:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,
里边的小四边形也为正方形,边长为b﹣a,
则有c2=ab×4+(b﹣a)2,
整理得:c2=a2+b2.
故选:D.
二、填空题(每小题3分,共30分)
11.(3分)计算: = 1.5 .
【解答】解:原式=(﹣)2016×(1.5)2016×1.5
=(﹣×1.5)2016×1.5
=1.5,
故答案为:1.5.
12.(3分)若代数式2a2+3a+1的值为6,则代数式6a2+9a﹣5= 10 .
【解答】解:∵2a2+3a+1的值为6.
∴2a2+3a=5,
∴6a2+9a﹣5=3(2a2+3a)﹣5=3×5﹣5=10.
故答案是:10.
13.(3分)设x﹣=1,则x2+= 3 .
【解答】解:∵x﹣=1,
∴x2+==12+2=1+2=3,
故答案为:3.
14.(3分)若x2+8x+18﹣2k=(x+4)2,则k= 1 .
【解答】解:(x+4)2=x2+8x+16,
∵x2+8x+18﹣2k=(x+4)2,
∴18﹣2k=16,
解得:k=1,
故答案为:1.
15.(3分)如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为 18cm .21cnjy.com
【解答】解:∵DE垂直平分AC,
∴EA=EC.
△EBC的周长=BC+BE+EC,
=BC+BE+AE,
=BC+AB,
=8+10,
=18(cm).
故答案为:18cm.
16.(3分)已知x≠1,(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4,…21·cn·jy·com
观察上式,猜想计算:(1﹣2)(1+2+22+23+24+25)= ﹣63 .
【解答】解:由题意可得:
(1﹣2)(1+2+22+23+24+25)
=1﹣26
=﹣63.
故答案为:﹣63.
17.(3分)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为 4cm或8cm .【21·世纪·教育·网】
【解答】解:如图,AB=AC,BD是中点,
根据题意得:(AB+AD)﹣(BC+CD)=2cm或(BC+CD)﹣(AB+AD)=2cm,
则AB﹣BC=2cm或BC﹣AB=2cm,
∵BC=6cm,
∴AB=8cm或4cm.
∴腰长为:4cm或8cm.
故答案为:4cm或8cm.
18.(3分)如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于 60° .
【解答】解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°,
∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°,
∴∠CDE=180°﹣(∠ECD+∠CED)=180°﹣90°=90°,
∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°,
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故答案为:60°.
19.(3分)如图,在三角形ABC中,AB=AC=BD,∠1=70°,则∠2的度数是 30° .
【解答】解:∵AB=BD,
∴∠BAD=∠1=70°,
∴∠B=180°﹣70°﹣70°=40°,
∵AB=AC,
∴∠C=∠B=40°,
∴∠2=∠1﹣∠C=30°,
故答案为:30°.
20.(3分)如图,在Rt△ABC,AC=BC,∠ACB=90°,AD是∠BAC的角平分线,若AD=8,则△ABD的面积为 16 .2·1·c·n·j·y
【解答】解:如图,过点D作DE⊥AB于E,
∵∠ACB=90°,AD是∠BAC的角平分线,
∴DE=CD,
设DE=x,
∵Rt△ABC,AC=BC,
∴∠B=45°,
∴△BDE是等腰直角三角形,
∴BD=DE=x,
∴BC=CD+BD=x+x,
在Rt△ACD中,根据勾股定理得,AC2+CD2=AD2,
即(x+x)2+x2=82,
解得x2=16(2﹣),
∵AC=BC,∠ACB=90°,
∴AB=BC=(x+x)=(2+)x,
∴△ABD的面积=AB?DE=×(2+)x?x=×(2+)×16(2﹣)=16.
故答案为:16.
三、解答题(共60分,其中22、24题各7分,21、23各8分,25--27题各10分)
21.(8分)计算:
(1)2(x2)3?x3﹣(3x3)3+(5x)2?x7
(2)(x4y+6x3y2﹣x2y3)÷(3x2y)
(3)(a+2b﹣3)(a﹣2b+3)
(4)简便计算:22016﹣22015.
【解答】解:(1)原式=2x6?x3﹣27x9+25x2?x7
=2x9﹣27x9+25x9
=0
(2)原式=x2﹣2xy﹣y2
(3)原式=[a+(2b﹣3)][a﹣(2b﹣3)]
=a2﹣(2b﹣3)2
=a2﹣4b2+12b﹣9
(4)原式=2×22015﹣22015=22015
22.(7分)先化简,再求值:(2x+1)2﹣(2x+1)(2x﹣1)+(x+1)(x﹣2)﹣x0,其中x=﹣1.21·世纪*教育网
【解答】解:(2x+1)2﹣(2x+1)(2x﹣1)+(x+1)(x﹣2)﹣x0
=4x2+4x+1﹣4x2+1+x2﹣x﹣2﹣1
=x2+3x﹣2,
把x=﹣1代入得:
原式=(﹣1)2+3×(﹣1)﹣2
=1﹣3﹣2
=﹣4.
23.(8分)将下列各式分解因式
(1)9x3﹣25xy2
(2)﹣3x+6x2﹣3x3
(3)(x+y)2﹣(x﹣y)2
(4)x2﹣1+y2﹣2xy.
【解答】解:(1)9x3﹣25xy2
=x(9x2﹣25y2)
=x(3x+5y)(3x﹣5y);
(2)﹣3x+6x2﹣3x3
=﹣3x(1﹣2x+x2)
﹣3x(x﹣1)2;
(3)(x+y)2﹣(x﹣y)2
=[(x+y)+(x﹣y)][(x+y)﹣(x﹣y)]
=2x×2y
=4xy;
(4)x2﹣1+y2﹣2xy
=(x2﹣2xy+y2)﹣1
=(x﹣y)2﹣1
=[(x﹣y)+1][(x﹣y)﹣1]
=(x﹣y+1)(x﹣y﹣1).
24.(7分)已知:如图,已知△ABC,
(1)分别画出与△ABC关于y轴对称的图形△A1B1C1
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
【解答】解:(1)所作图形如图所示;
(2)A1(0,﹣2),B1(﹣2,﹣4),C1(﹣4,﹣1);
(3)S△ABC=3×4﹣×2×3﹣×4×1﹣×2×2=12﹣3﹣2﹣2=5.
25.(10分)已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.求证:①BE=CD;②△AMN是等腰三角形.www-2-1-cnjy-com
【解答】证明:①∵∠BAC=∠DAE,
∴∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△ABE≌△ACD(SAS),
∴BE=CD.
②∵△ABE≌△ACD,
∴∠ABE=∠ACD,BE=CD,
∵M、N分别是BE,CD的中点,
∴BM=CN.
又∵AB=AC,
∴△ABM≌△ACN.
∴AM=AN,
即△AMN为等腰三角形.
26.(10分)为了援助失学儿童,初三学生李飞从2016年1月份开始,每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内.已知2月份存款后清点储蓄盒内有存款80元,5月份存款后清点储蓄盒内有存款125元.
(1)在李飞2016年1月份存款前,储蓄盒内已有存款多少元?
(2)为了实现2019年6月份存款后存款总数超过1000元的目标,李飞计划从2017年1月份开始,每月存款都比2016年每月存款多t元(t为整数),求t的最小值.2-1-c-n-j-y
【解答】解:(1)设李飞每月存款x元,储蓄盒内原有存款y元,依题意得,
,
解得,
答:李飞2016年1月份存款前,储蓄盒内已有存款50元;
(2)由(1)得,李飞2016年共有存款12×15+50=230元,
2017年1月份后每月存入(15+t)元,
2017年1月到2019年6月共有30个月,
依題意得,230+30(15+t)>1000,
解得t>10,
因为t为整数,
所以t的最小值为11.
答:t的最小值为11.
27.(10分)如图,在平面直角坐标系中,AB=BE,AE=12,∠BAO=30°,点C与点O关于直线BE对称.21*cnjy*com
(1)求CE的长;
(2)动点N从E出发,以1个单位/秒的速度沿射线EC方向运动,过N作x轴的平行线交直线OC于G,设△CGN的周长为C,运动时间为t秒,请用含t的式子表示C;【21cnj*y.co*m】
(3)在(2)的条件下,动点M从A以1个单位/秒的速度沿射线AE运动,且点M与点N同时出发,MN与射线OC相交于点K.是否存在某一运动时间t,使得=2.若存在请求出t值;若不存在,请说明理由.21*教*育*名*师
【解答】解:(1)如图1中,
∵BA=BE,BO⊥AE,AE=12,
∴OA=OE=6,∠BAO=∠BEO=30°,
∵O、C关于直线BE对称,
∴EC=EO=6.
(2)如图2中,
∵O、C关于直线BE对称,
∴EC=EO=6,∠BEO=∠BEC=30°,
∴∠OEC=60°,
∴△COE是等边三角形,
∵NG∥OE,
∴∠CGN=∠COE=60°,∠CNG=∠CEO=60°,
∴△CNG是等边三角形,
①当0<t<6时,C=3CN=3(6﹣t)=18﹣3t.
②当t>6时,同法可证△CN′G′是等边三角形,C=3CN′=3(t﹣6)=3t﹣18.
(3)如图3中,取OK的中点H,连接MH.
∵OK=2OM,OH=KH,
∴OH=OM,∵∠HOM=60°,
∴△OMH是等边三角形,
∴HM=OH=HK,
∴△OMK是直角三角形,
∴∠OMK=∠NME=90°,
∵∠NEM=60°,
∴∠MNE=30°,
∴EN=2EM,
∴t=2(12﹣t),
解得t=8,
∴t=8s时, =2.
一、选择题(每小题3分,共30分)
1.(3分)下列运算正确的是( )
A.x3+x3=2x6 B.x2?x4=x8 C.(xy)m=xym D.(﹣x5)4=x20
2.(3分)若(x+2)(x﹣3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=6 B.a=﹣1,b=6 C.a=5,b=﹣6 D.a=﹣1,b=﹣6
3.(3分)下列图形中,轴对称图形的个数是( )
A.1 B.2 C.3 D.4
4.(3分)若(x+y﹣3)2+(x﹣y+5)2=0.则x2﹣y2的值是( )
A.8 B.﹣8 C.15 D.﹣15
5.(3分)若(x﹣a)(x﹣5)的展开式中不含有x的一次项,则a的值为( )
A.0 B.5 C.﹣5 D.5或﹣5
6.(3分)到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线交点 B.三条角平分线交点
C.三条高的交点 D.三条边的垂直平分线交点
7.(3分)若x2﹣2(m﹣3)x+16是完全平方式,则m的值等于( )
A.﹣1 B.7 C.7或﹣7 D.7或﹣1
8.(3分)n个底边长为a,腰长为b的等腰△ABC拼成图,则图中的线段之和是( )
A.na+2nb B.na+nb+b C.na+2b D.2na+2b
9.(3分)下列说法中,正确的个数有( )
(1)关于某直线对称的两个三角形是全等三角形
(2)全等三角形是关于某直线对称的
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称
(5)轴对称图形的对应点所连线段被对称轴垂直平分
(6)等腰三角形的角平分线、中线、高线互相重合.
A.2 B.3 C.4 D.5
10.(3分)用四个完全一样的边长分别为a、b、c的直角三角板拼成图所示的图形,则下列结论中正确的是( )21教育网
A.c2=(a+b)2 B.c2=a2+2ab+b2 C.c2=a2﹣2ab+b2 D.c2=a2+b2
二、填空题(每小题3分,共30分)
11.(3分)计算: = .
12.(3分)若代数式2a2+3a+1的值为6,则代数式6a2+9a﹣5= .
13.(3分)设x﹣=1,则x2+= .
14.(3分)若x2+8x+18﹣2k=(x+4)2,则k= .
15.(3分)如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为 .www.21-cn-jy.com
16.(3分)已知x≠1,(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4,…【21教育名师】
观察上式,猜想计算:(1﹣2)(1+2+22+23+24+25)= .
17.(3分)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为 .【21教育】
18.(3分)如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于 .
19.(3分)如图,在三角形ABC中,AB=AC=BD,∠1=70°,则∠2的度数是 .
20.(3分)如图,在Rt△ABC,AC=BC,∠ACB=90°,AD是∠BAC的角平分线,若AD=8,则△ABD的面积为 .21-cnjy*com
三、解答题(共60分,其中22、24题各7分,21、23各8分,25--27题各10分)
21.(8分)计算:
(1)2(x2)3?x3﹣(3x3)3+(5x)2?x7
(2)(x4y+6x3y2﹣x2y3)÷(3x2y)
(3)(a+2b﹣3)(a﹣2b+3)
(4)简便计算:22016﹣22015.
22.(7分)先化简,再求值:(2x+1)2﹣(2x+1)(2x﹣1)+(x+1)(x﹣2)﹣x0,其中x=﹣1.
23.(8分)将下列各式分解因式
(1)9x3﹣25xy2
(2)﹣3x+6x2﹣3x3
(3)(x+y)2﹣(x﹣y)2
(4)x2﹣1+y2﹣2xy.
24.(7分)已知:如图,已知△ABC,
(1)分别画出与△ABC关于y轴对称的图形△A1B1C1
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
25.(10分)已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.求证:①BE=CD;②△AMN是等腰三角形.
26.(10分)为了援助失学儿童,初三学生李飞从2016年1月份开始,每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内.已知2月份存款后清点储蓄盒内有存款80元,5月份存款后清点储蓄盒内有存款125元.
(1)在李飞2016年1月份存款前,储蓄盒内已有存款多少元?
(2)为了实现2019年6月份存款后存款总数超过1000元的目标,李飞计划从2017年1月份开始,每月存款都比2016年每月存款多t元(t为整数),求t的最小值.
27.(10分)如图,在平面直角坐标系中,AB=BE,AE=12,∠BAO=30°,点C与点O关于直线BE对称.
(1)求CE的长;
(2)动点N从E出发,以1个单位/秒的速度沿射线EC方向运动,过N作x轴的平行线交直线OC于G,设△CGN的周长为C,运动时间为t秒,请用含t的式子表示C;
(3)在(2)的条件下,动点M从A以1个单位/秒的速度沿射线AE运动,且点M与点N同时出发,MN与射线OC相交于点K.是否存在某一运动时间t,使得=2.若存在请求出t值;若不存在,请说明理由.
2016-2017学年黑龙江省哈尔滨156中八年级(上)期中数学试卷(五四学制)
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列运算正确的是( )
A.x3+x3=2x6 B.x2?x4=x8 C.(xy)m=xym D.(﹣x5)4=x20
【解答】解:A、x3+x3=2x3,故原题计算错误;
B、x2?x4=x6,故原题计算错误;
C、(xy)m=xmym,故原题计算错误;
D、(﹣x5)4=x20,故原题计算正确;
故选:D.
2.(3分)若(x+2)(x﹣3)=x2+ax+b,则a,b的值分别为( )
A.a=5,b=6 B.a=﹣1,b=6 C.a=5,b=﹣6 D.a=﹣1,b=﹣6
【解答】解:∵(x+2)(x﹣3)=x2﹣x﹣6=x2+ax+b,
∴a=﹣1,b=﹣6.
故选:D.
3.(3分)下列图形中,轴对称图形的个数是( )
A.1 B.2 C.3 D.4
【解答】解:中间两个图形是轴对称图形,轴对称图形的个数是2,故选B.
4.(3分)若(x+y﹣3)2+(x﹣y+5)2=0.则x2﹣y2的值是( )
A.8 B.﹣8 C.15 D.﹣15
【解答】解:∵(x+y﹣3)2+(x﹣y+5)2=0,
∴,
解得,
∴x2﹣y2=1﹣16=﹣15.
故选:D.
5.(3分)若(x﹣a)(x﹣5)的展开式中不含有x的一次项,则a的值为( )
A.0 B.5 C.﹣5 D.5或﹣5
【解答】解:(x﹣a)(x﹣5)
=x2﹣5x﹣ax+5a
=x2+(﹣5﹣a)x+5a,
∵(x﹣a)(x﹣5)的展开式中不含有x的一次项,
∴﹣5﹣a=0,
a=﹣5.
故选:C.
6.(3分)到△ABC的三条边距离相等的点是△ABC的( )
A.三条中线交点 B.三条角平分线交点
C.三条高的交点 D.三条边的垂直平分线交点
【解答】解:∵到△ABC的三条边距离相等,
∴这点在这个三角形三条角平分线上,
即这点是三条角平分线的交点.
故选:B.
7.(3分)若x2﹣2(m﹣3)x+16是完全平方式,则m的值等于( )
A.﹣1 B.7 C.7或﹣7 D.7或﹣1
【解答】解:依题意,得m﹣3=±4,
解得m=7或﹣1.
故选:D.
8.(3分)n个底边长为a,腰长为b的等腰△ABC拼成图,则图中的线段之和是( )
A.na+2nb B.na+nb+b C.na+2b D.2na+2b
【解答】解:当有2个等腰三角形时,线段之和为:2a+3b
当有3个等腰三角形时,线段之和为:3a+4b
当有4个等腰三角形时,线段之和为:4a+5b
…
当有n个等腰三角形时,线段之和为:na+(n+1)b=na+nb+b
故选:B.
9.(3分)下列说法中,正确的个数有( )
(1)关于某直线对称的两个三角形是全等三角形
(2)全等三角形是关于某直线对称的
(3)两个图形关于某直线对称,则这两个图形一定分别位于这条直线的两侧
(4)有一条公共边的两个全等三角形关于公共边所在的直线对称
(5)轴对称图形的对应点所连线段被对称轴垂直平分
(6)等腰三角形的角平分线、中线、高线互相重合.
A.2 B.3 C.4 D.5
【解答】解:(1)关于某直线对称的两个三角形是全等三角形,正确;
(2)全等三角形不一定关于某直线对称的,错误;
(3)两个图形关于某直线对称,则这两个图形不一定分别位于这条直线的两侧,错误;
(4)有一条公共边的两个全等三角形不一定关于公共边所在的直线对称,错误;
(5)轴对称图形的对应点所连线段被对称轴垂直平分,正确;
(6)等腰三角形的角平分线、中线、高线互相重合.正确;
故选:B.
10.(3分)用四个完全一样的边长分别为a、b、c的直角三角板拼成图所示的图形,则下列结论中正确的是( )21世纪教育网
A.c2=(a+b)2 B.c2=a2+2ab+b2 C.c2=a2﹣2ab+b2 D.c2=a2+b2
【解答】解:由题意得到四个完全一样的直角三角板围成的四边形为正方形,其边长为c,
里边的小四边形也为正方形,边长为b﹣a,
则有c2=ab×4+(b﹣a)2,
整理得:c2=a2+b2.
故选:D.
二、填空题(每小题3分,共30分)
11.(3分)计算: = 1.5 .
【解答】解:原式=(﹣)2016×(1.5)2016×1.5
=(﹣×1.5)2016×1.5
=1.5,
故答案为:1.5.
12.(3分)若代数式2a2+3a+1的值为6,则代数式6a2+9a﹣5= 10 .
【解答】解:∵2a2+3a+1的值为6.
∴2a2+3a=5,
∴6a2+9a﹣5=3(2a2+3a)﹣5=3×5﹣5=10.
故答案是:10.
13.(3分)设x﹣=1,则x2+= 3 .
【解答】解:∵x﹣=1,
∴x2+==12+2=1+2=3,
故答案为:3.
14.(3分)若x2+8x+18﹣2k=(x+4)2,则k= 1 .
【解答】解:(x+4)2=x2+8x+16,
∵x2+8x+18﹣2k=(x+4)2,
∴18﹣2k=16,
解得:k=1,
故答案为:1.
15.(3分)如图,DE是△ABC中AC边的垂直平分线,若BC=8cm,AB=10cm,则△EBC的周长为 18cm .21cnjy.com
【解答】解:∵DE垂直平分AC,
∴EA=EC.
△EBC的周长=BC+BE+EC,
=BC+BE+AE,
=BC+AB,
=8+10,
=18(cm).
故答案为:18cm.
16.(3分)已知x≠1,(1﹣x)(1+x)=1﹣x2,(1﹣x)(1+x+x2)=1﹣x3,(1﹣x)(1+x+x2+x3)=1﹣x4,…21·cn·jy·com
观察上式,猜想计算:(1﹣2)(1+2+22+23+24+25)= ﹣63 .
【解答】解:由题意可得:
(1﹣2)(1+2+22+23+24+25)
=1﹣26
=﹣63.
故答案为:﹣63.
17.(3分)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为 4cm或8cm .【21·世纪·教育·网】
【解答】解:如图,AB=AC,BD是中点,
根据题意得:(AB+AD)﹣(BC+CD)=2cm或(BC+CD)﹣(AB+AD)=2cm,
则AB﹣BC=2cm或BC﹣AB=2cm,
∵BC=6cm,
∴AB=8cm或4cm.
∴腰长为:4cm或8cm.
故答案为:4cm或8cm.
18.(3分)如图,若∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于 60° .
【解答】解:∵AB=BC=CD=DE=EF,∠A=15°,
∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°,
∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°,
∴∠CDE=180°﹣(∠ECD+∠CED)=180°﹣90°=90°,
∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°,
∴∠DEF=180°﹣(∠EDF+∠EFD)=180°﹣120°=60°.
故答案为:60°.
19.(3分)如图,在三角形ABC中,AB=AC=BD,∠1=70°,则∠2的度数是 30° .
【解答】解:∵AB=BD,
∴∠BAD=∠1=70°,
∴∠B=180°﹣70°﹣70°=40°,
∵AB=AC,
∴∠C=∠B=40°,
∴∠2=∠1﹣∠C=30°,
故答案为:30°.
20.(3分)如图,在Rt△ABC,AC=BC,∠ACB=90°,AD是∠BAC的角平分线,若AD=8,则△ABD的面积为 16 .2·1·c·n·j·y
【解答】解:如图,过点D作DE⊥AB于E,
∵∠ACB=90°,AD是∠BAC的角平分线,
∴DE=CD,
设DE=x,
∵Rt△ABC,AC=BC,
∴∠B=45°,
∴△BDE是等腰直角三角形,
∴BD=DE=x,
∴BC=CD+BD=x+x,
在Rt△ACD中,根据勾股定理得,AC2+CD2=AD2,
即(x+x)2+x2=82,
解得x2=16(2﹣),
∵AC=BC,∠ACB=90°,
∴AB=BC=(x+x)=(2+)x,
∴△ABD的面积=AB?DE=×(2+)x?x=×(2+)×16(2﹣)=16.
故答案为:16.
三、解答题(共60分,其中22、24题各7分,21、23各8分,25--27题各10分)
21.(8分)计算:
(1)2(x2)3?x3﹣(3x3)3+(5x)2?x7
(2)(x4y+6x3y2﹣x2y3)÷(3x2y)
(3)(a+2b﹣3)(a﹣2b+3)
(4)简便计算:22016﹣22015.
【解答】解:(1)原式=2x6?x3﹣27x9+25x2?x7
=2x9﹣27x9+25x9
=0
(2)原式=x2﹣2xy﹣y2
(3)原式=[a+(2b﹣3)][a﹣(2b﹣3)]
=a2﹣(2b﹣3)2
=a2﹣4b2+12b﹣9
(4)原式=2×22015﹣22015=22015
22.(7分)先化简,再求值:(2x+1)2﹣(2x+1)(2x﹣1)+(x+1)(x﹣2)﹣x0,其中x=﹣1.21·世纪*教育网
【解答】解:(2x+1)2﹣(2x+1)(2x﹣1)+(x+1)(x﹣2)﹣x0
=4x2+4x+1﹣4x2+1+x2﹣x﹣2﹣1
=x2+3x﹣2,
把x=﹣1代入得:
原式=(﹣1)2+3×(﹣1)﹣2
=1﹣3﹣2
=﹣4.
23.(8分)将下列各式分解因式
(1)9x3﹣25xy2
(2)﹣3x+6x2﹣3x3
(3)(x+y)2﹣(x﹣y)2
(4)x2﹣1+y2﹣2xy.
【解答】解:(1)9x3﹣25xy2
=x(9x2﹣25y2)
=x(3x+5y)(3x﹣5y);
(2)﹣3x+6x2﹣3x3
=﹣3x(1﹣2x+x2)
﹣3x(x﹣1)2;
(3)(x+y)2﹣(x﹣y)2
=[(x+y)+(x﹣y)][(x+y)﹣(x﹣y)]
=2x×2y
=4xy;
(4)x2﹣1+y2﹣2xy
=(x2﹣2xy+y2)﹣1
=(x﹣y)2﹣1
=[(x﹣y)+1][(x﹣y)﹣1]
=(x﹣y+1)(x﹣y﹣1).
24.(7分)已知:如图,已知△ABC,
(1)分别画出与△ABC关于y轴对称的图形△A1B1C1
(2)写出△A1B1C1各顶点坐标;
(3)求△ABC的面积.
【解答】解:(1)所作图形如图所示;
(2)A1(0,﹣2),B1(﹣2,﹣4),C1(﹣4,﹣1);
(3)S△ABC=3×4﹣×2×3﹣×4×1﹣×2×2=12﹣3﹣2﹣2=5.
25.(10分)已知:如图所示,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.求证:①BE=CD;②△AMN是等腰三角形.www-2-1-cnjy-com
【解答】证明:①∵∠BAC=∠DAE,
∴∠BAE=∠CAD,
∵AB=AC,AD=AE,
∴△ABE≌△ACD(SAS),
∴BE=CD.
②∵△ABE≌△ACD,
∴∠ABE=∠ACD,BE=CD,
∵M、N分别是BE,CD的中点,
∴BM=CN.
又∵AB=AC,
∴△ABM≌△ACN.
∴AM=AN,
即△AMN为等腰三角形.
26.(10分)为了援助失学儿童,初三学生李飞从2016年1月份开始,每月一次将相等数额的零用钱存入已有部分存款的储蓄盒内.已知2月份存款后清点储蓄盒内有存款80元,5月份存款后清点储蓄盒内有存款125元.
(1)在李飞2016年1月份存款前,储蓄盒内已有存款多少元?
(2)为了实现2019年6月份存款后存款总数超过1000元的目标,李飞计划从2017年1月份开始,每月存款都比2016年每月存款多t元(t为整数),求t的最小值.2-1-c-n-j-y
【解答】解:(1)设李飞每月存款x元,储蓄盒内原有存款y元,依题意得,
,
解得,
答:李飞2016年1月份存款前,储蓄盒内已有存款50元;
(2)由(1)得,李飞2016年共有存款12×15+50=230元,
2017年1月份后每月存入(15+t)元,
2017年1月到2019年6月共有30个月,
依題意得,230+30(15+t)>1000,
解得t>10,
因为t为整数,
所以t的最小值为11.
答:t的最小值为11.
27.(10分)如图,在平面直角坐标系中,AB=BE,AE=12,∠BAO=30°,点C与点O关于直线BE对称.21*cnjy*com
(1)求CE的长;
(2)动点N从E出发,以1个单位/秒的速度沿射线EC方向运动,过N作x轴的平行线交直线OC于G,设△CGN的周长为C,运动时间为t秒,请用含t的式子表示C;【21cnj*y.co*m】
(3)在(2)的条件下,动点M从A以1个单位/秒的速度沿射线AE运动,且点M与点N同时出发,MN与射线OC相交于点K.是否存在某一运动时间t,使得=2.若存在请求出t值;若不存在,请说明理由.21*教*育*名*师
【解答】解:(1)如图1中,
∵BA=BE,BO⊥AE,AE=12,
∴OA=OE=6,∠BAO=∠BEO=30°,
∵O、C关于直线BE对称,
∴EC=EO=6.
(2)如图2中,
∵O、C关于直线BE对称,
∴EC=EO=6,∠BEO=∠BEC=30°,
∴∠OEC=60°,
∴△COE是等边三角形,
∵NG∥OE,
∴∠CGN=∠COE=60°,∠CNG=∠CEO=60°,
∴△CNG是等边三角形,
①当0<t<6时,C=3CN=3(6﹣t)=18﹣3t.
②当t>6时,同法可证△CN′G′是等边三角形,C=3CN′=3(t﹣6)=3t﹣18.
(3)如图3中,取OK的中点H,连接MH.
∵OK=2OM,OH=KH,
∴OH=OM,∵∠HOM=60°,
∴△OMH是等边三角形,
∴HM=OH=HK,
∴△OMK是直角三角形,
∴∠OMK=∠NME=90°,
∵∠NEM=60°,
∴∠MNE=30°,
∴EN=2EM,
∴t=2(12﹣t),
解得t=8,
∴t=8s时, =2.
同课章节目录
