苏教版小学六年级数学上 1 长方体和正方体的体积 (共20张PPT)
文档属性
| 名称 | 苏教版小学六年级数学上 1 长方体和正方体的体积 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 670.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-07 10:07:48 | ||
图片预览



文档简介
(共20张PPT)
1.3 长方体和正方体的体积
(教材第10~11页)
1.长方体和正方体
课题引入
你知道的单位有哪些?用字母怎么表示?
(cm3)
(dm3)
(m3)
(cm)
(dm)
(m)
立方厘米
立方分米
立方米
厘米
分米
米
平方厘米
平方分米
平方米
(cm2)
(dm2)
(m2)
体 积
长 度
面 积
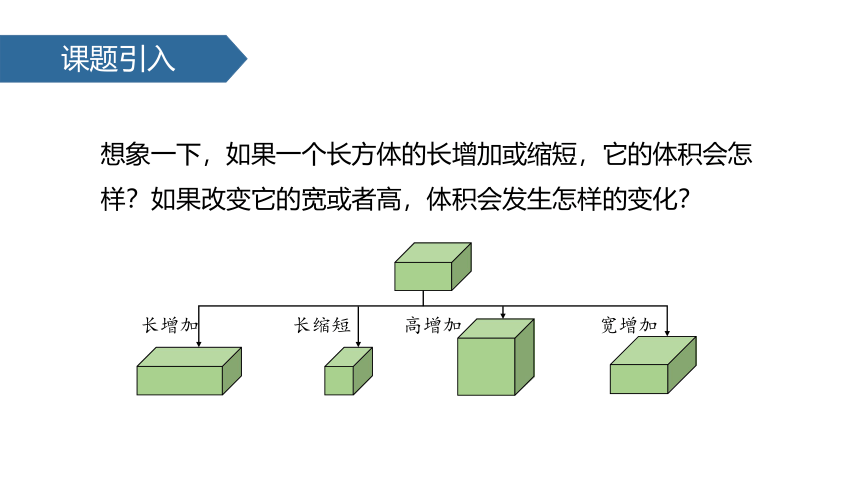
课题引入
想象一下,如果一个长方体的长增加或缩短,它的体积会怎样?如果改变它的宽或者高,体积会发生怎样的变化?
长增加
长缩短
高增加
宽增加
教学新知
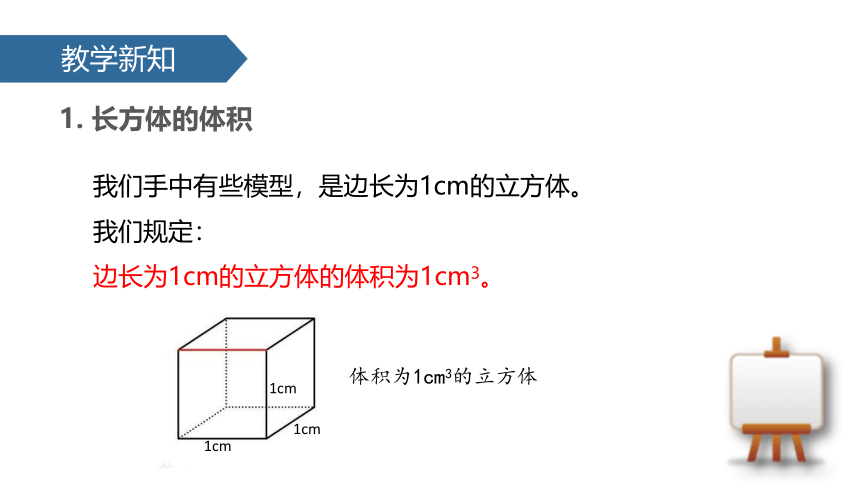
1. 长方体的体积
我们手中有些模型,是边长为1cm的立方体。
我们规定:
边长为1cm的立方体的体积为1cm3。
1cm
1cm
1cm
体积为1cm3的立方体
教学新知
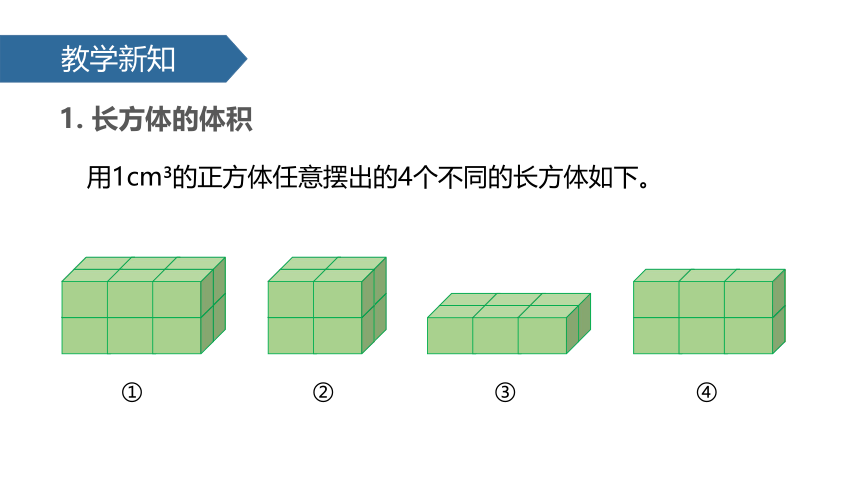
1. 长方体的体积
请同学们一起来摆出一些长方体:
(1)同桌合作,用若干个1cm 的正方体任意摆出4个不 同的长方体并编上序号。
(2)观察摆出的长方体的长、宽、高,所用小正方体的个数,以及它们的体积各是多少,完成记录表。
(3)填完表格后,同桌核对数据,并交流自己的发现。
教学新知
1. 长方体的体积
①
②
③
④
用1cm 的正方体任意摆出的4个不同的长方体如下。
教学新知
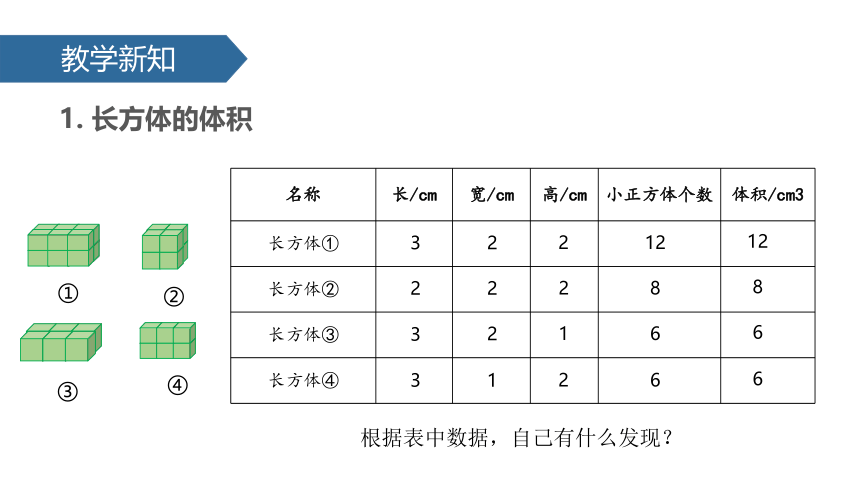
1. 长方体的体积
名称 长/cm 宽/cm 高/cm 小正方体个数 体积/cm3
长方体①
长方体②
长方体③
长方体④
3
2
2
12
12
2
2
2
8
8
3
3
2
2
1
1
6
6
6
6
根据表中数据,自己有什么发现?
①
②
③
④
教学新知
1. 长方体的体积
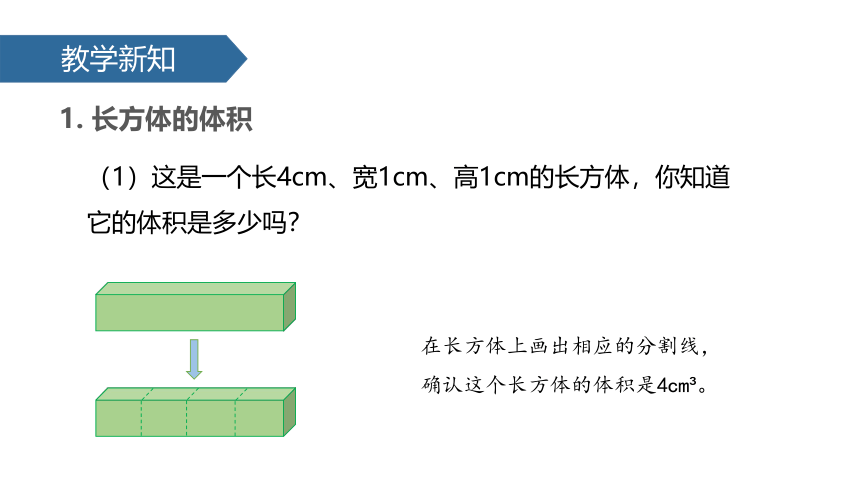
(1)这是一个长4cm、宽1cm、高1cm的长方体,你知道它的体积是多少吗?
在长方体上画出相应的分割线,确认这个长方体的体积是4cm 。
教学新知
1. 长方体的体积
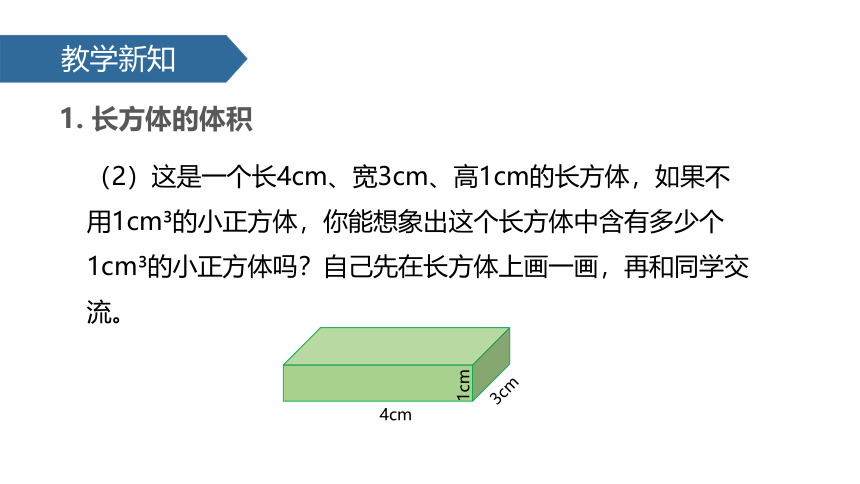
(2)这是一个长4cm、宽3cm、高1cm的长方体,如果不用1cm 的小正方体,你能想象出这个长方体中含有多少个1cm 的小正方体吗?自己先在长方体上画一画,再和同学交流。
4cm
3cm
1cm
教学新知
1. 长方体的体积
在这个长方体中,沿着长一排可以摆4个1cm 的小正方体,沿着宽可以摆3排,所以,可以用“4×3×1”来计算出这个长方体的体积为12cm 。
教学新知
1. 长方体的体积
(3)再来看这个长方体,它的长、宽、高分别是几cm?你能想象出这个长方体中含有多少个1cm 的小正方体吗?自己先试一试。
延着长一排可以摆4个小正方形,沿着宽一排可以摆3个,沿着高可以摆2层。用4×3×2计算体积为24cm 。
教学新知
1. 长方体的体积
如果用V表示长方体的体积,a、b、h分别表示长方体的长、宽、高,你能用字母表示出长方体的体积公式吗?
长方体的体积=长×宽×高
V= abh
教学新知
2. 正长方体的体积
正方体是特殊的长方体,想一想正方体的棱长有什么特点?如果正方体的棱长为a,你能根据长方体的体积公式直接写出正方体的体积公式吗?
正方体的体积=长×宽×高
V= aaa=a3
边长为1cm时,体积 V=1cm × 1cm×1cm=1cm3
知识梳理
长方体和正方体的体积
V=abh
V=a
课堂练习
答:长方体包装盒的体积为:28.5×12×10=3420cm
正方体包装盒的体积为:12×12×12=1728cm
1. 算出右边两个包装盒的体积各是多少立方厘米?
课堂练习
2. 下面的长方体和正方体都是用1立方厘米的正方体摆成的。
(1)长方体的长、宽、高分别是多少?正方体的棱长呢?
(2)它们的体积分别是多少?
课堂练习
【讲评】
长、宽、高为:
3cm、2cm、4cm
体积为:
3×2×4=24cm
长、宽、高为:
6cm、3cm、2cm
体积为:
6×3×2=36cm
棱长为:3cm
体积为:3×3×3=27cm
课堂练习
3. 计算。
33
53
13
103
0.13
= 27
= 125
= 1
= 1000
= 0.001
课后作业
回家后找一找自己以前用过的长方体或正方体模型,或是家里的长方体或正方体物品,选用合适的单位量一量它们的长宽高,再求一求它们的表面积和体积。
知识拓展
计算物体容积和体积的方法相同,不少同学认为“容积”就是“体积”。其实,“容积”和“体积”是两个不同的概念,它们是有什么区别?
1.3 长方体和正方体的体积
(教材第10~11页)
1.长方体和正方体
课题引入
你知道的单位有哪些?用字母怎么表示?
(cm3)
(dm3)
(m3)
(cm)
(dm)
(m)
立方厘米
立方分米
立方米
厘米
分米
米
平方厘米
平方分米
平方米
(cm2)
(dm2)
(m2)
体 积
长 度
面 积
课题引入
想象一下,如果一个长方体的长增加或缩短,它的体积会怎样?如果改变它的宽或者高,体积会发生怎样的变化?
长增加
长缩短
高增加
宽增加
教学新知
1. 长方体的体积
我们手中有些模型,是边长为1cm的立方体。
我们规定:
边长为1cm的立方体的体积为1cm3。
1cm
1cm
1cm
体积为1cm3的立方体
教学新知
1. 长方体的体积
请同学们一起来摆出一些长方体:
(1)同桌合作,用若干个1cm 的正方体任意摆出4个不 同的长方体并编上序号。
(2)观察摆出的长方体的长、宽、高,所用小正方体的个数,以及它们的体积各是多少,完成记录表。
(3)填完表格后,同桌核对数据,并交流自己的发现。
教学新知
1. 长方体的体积
①
②
③
④
用1cm 的正方体任意摆出的4个不同的长方体如下。
教学新知
1. 长方体的体积
名称 长/cm 宽/cm 高/cm 小正方体个数 体积/cm3
长方体①
长方体②
长方体③
长方体④
3
2
2
12
12
2
2
2
8
8
3
3
2
2
1
1
6
6
6
6
根据表中数据,自己有什么发现?
①
②
③
④
教学新知
1. 长方体的体积
(1)这是一个长4cm、宽1cm、高1cm的长方体,你知道它的体积是多少吗?
在长方体上画出相应的分割线,确认这个长方体的体积是4cm 。
教学新知
1. 长方体的体积
(2)这是一个长4cm、宽3cm、高1cm的长方体,如果不用1cm 的小正方体,你能想象出这个长方体中含有多少个1cm 的小正方体吗?自己先在长方体上画一画,再和同学交流。
4cm
3cm
1cm
教学新知
1. 长方体的体积
在这个长方体中,沿着长一排可以摆4个1cm 的小正方体,沿着宽可以摆3排,所以,可以用“4×3×1”来计算出这个长方体的体积为12cm 。
教学新知
1. 长方体的体积
(3)再来看这个长方体,它的长、宽、高分别是几cm?你能想象出这个长方体中含有多少个1cm 的小正方体吗?自己先试一试。
延着长一排可以摆4个小正方形,沿着宽一排可以摆3个,沿着高可以摆2层。用4×3×2计算体积为24cm 。
教学新知
1. 长方体的体积
如果用V表示长方体的体积,a、b、h分别表示长方体的长、宽、高,你能用字母表示出长方体的体积公式吗?
长方体的体积=长×宽×高
V= abh
教学新知
2. 正长方体的体积
正方体是特殊的长方体,想一想正方体的棱长有什么特点?如果正方体的棱长为a,你能根据长方体的体积公式直接写出正方体的体积公式吗?
正方体的体积=长×宽×高
V= aaa=a3
边长为1cm时,体积 V=1cm × 1cm×1cm=1cm3
知识梳理
长方体和正方体的体积
V=abh
V=a
课堂练习
答:长方体包装盒的体积为:28.5×12×10=3420cm
正方体包装盒的体积为:12×12×12=1728cm
1. 算出右边两个包装盒的体积各是多少立方厘米?
课堂练习
2. 下面的长方体和正方体都是用1立方厘米的正方体摆成的。
(1)长方体的长、宽、高分别是多少?正方体的棱长呢?
(2)它们的体积分别是多少?
课堂练习
【讲评】
长、宽、高为:
3cm、2cm、4cm
体积为:
3×2×4=24cm
长、宽、高为:
6cm、3cm、2cm
体积为:
6×3×2=36cm
棱长为:3cm
体积为:3×3×3=27cm
课堂练习
3. 计算。
33
53
13
103
0.13
= 27
= 125
= 1
= 1000
= 0.001
课后作业
回家后找一找自己以前用过的长方体或正方体模型,或是家里的长方体或正方体物品,选用合适的单位量一量它们的长宽高,再求一求它们的表面积和体积。
知识拓展
计算物体容积和体积的方法相同,不少同学认为“容积”就是“体积”。其实,“容积”和“体积”是两个不同的概念,它们是有什么区别?
