万有引力理论的成就(山东省烟台市)
文档属性
| 名称 | 万有引力理论的成就(山东省烟台市) |

|
|
| 格式 | rar | ||
| 文件大小 | 104.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2009-03-10 00:00:00 | ||
图片预览







文档简介
课件21张PPT。§7.4:万有引力理论的成就授课:格中栾景尧普通高中课程标准实验教科书
物理2必修
人民教育出版社
(新课标人教实验版)一:复习回顾,引入新课1:万有引力定律的内容是什么自然界中任何两个物体都是相互吸引的,引力的大小跟物体质量的乘积成正比,跟它们的距离的二次方成反比。2:万有引力定律的适用条件是什么①:定律适用于两质点之间;
②:“距离R”是指两质点中心之间的距离,当质点是
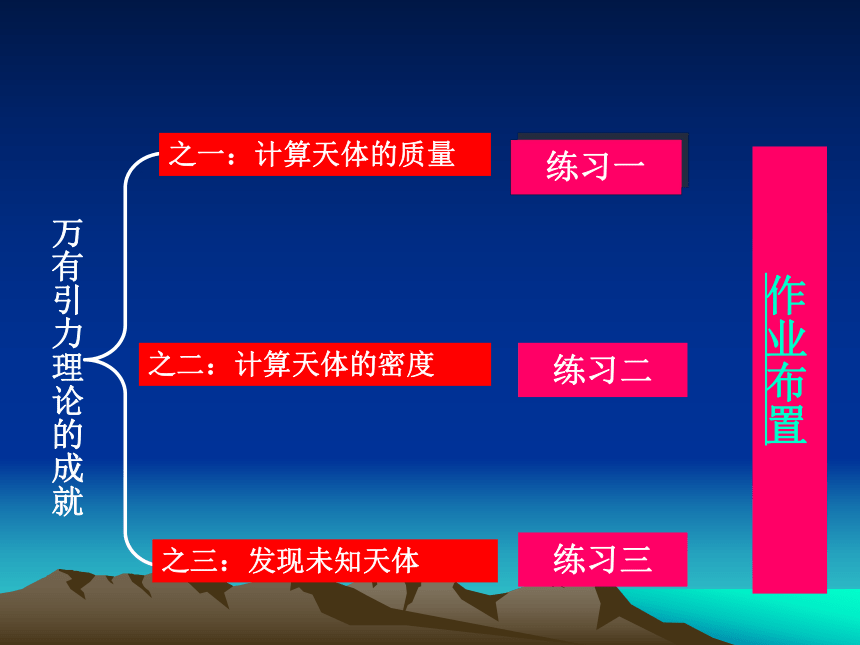
两均质球体时,R是指两球体球心之间的距离。 万有引力理论的成就之一:计算天体的质量之二:计算天体的密度之三:发现未知天体练习一练习二练习三二:万有引力理论的成就应用之一:计算天体的质量原理:对于有卫星的天体,可以认为卫星绕天体中心 做匀速圆周运动,天体对卫星的万有引力提供卫星做匀速圆周运动的向心力。1:若已知卫星绕天体做匀速圆周运动的轨道半径为r,卫
星运动的周期为T,据牛顿第二定律例1继续例1:登月密封舱在离月球表面h处的空中沿圆形轨道运行,
周期是T,已知月球的半径是R,万有引力常数是G,
据此试计算月球的质量。分析与解答返回2:若已知卫星绕中心天体做圆周运动的轨道半径为r,卫星
运动的线速度为v,据牛顿第二定律 3:若已知卫星运动的线速度v和运行周期T,则据牛顿第二
定律4:对于没有卫星的天体(或虽有卫星,但不知道有关卫
星运动的参量),不考虑天体自转的影响,根据万有
引力等于重力的关系来计算天体的质量
----------卡文迪许在 实验室”称量”地球的质量 R----------------为天体的半径g----------------天体表面的重力加速度返回
科学真是迷人。根据零星的事实,增添一点猜想,竟能赢得那么多的收获!
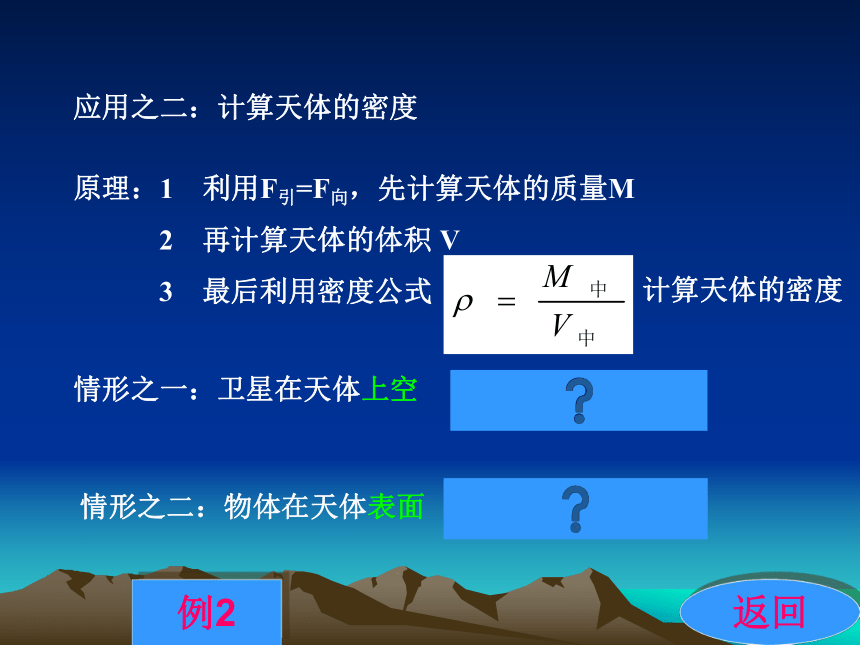
--马克·吐温应用之二:计算天体的密度原理:1 利用F引=F向,先计算天体的质量M
2 再计算天体的体积 V
3 最后利用密度公式计算天体的密度情形之一:卫星在天体上空情形之二:物体在天体表面例2返回设:m卫为环绕卫星质量;r 为环绕卫星的轨道半径;T为环绕卫星的周期。返回g 为中心天体表面的重力加速度;R 为中心天体的半径返回分别应用重力等于万有引力列式求m ,再运用题目
中的比例关系对密度比例化简求解。例2:一物体在某行星表面受到的吸引力为地球表面吸引力
的a倍,该行星半径是地球半径的b倍,若该行星和地
的质量分布都是均匀的,试求该星球密度和地球密度
之比。 解答解答设地球质量为m1 ,地球半径为R,某星球质量为m2
物体的质量为m 。∵∴则:某星球与地球的密度之比返回应用之三:发现未知天体-------- 万有引力定律的贡献背景:1781年由英国物理学家威廉.赫歇尔发现了天王
星,但人们观测到的天王星的运行轨迹与万有引
力定律推测的结果有一些误差,于是人们就推测
在天王星外面轨道上还应有其它星体…… 返回1. 1845年英国人亚当斯和法国天文学家勒维耶根据计算
“发现”了海王星(第8个行星)。
1846年9月23日晚,德国的伽勒在勒维耶预言的位置发现了该星。
2:1705年英国天文学家哈雷根据万有引力定律计算了一颗著名彗星的轨道,并正确预言了它的回归。
例3例4双星问题例3:两个星球组成双星,它们在相互之间的万有引力作用下
绕连线上的某点作匀速圆周运动,现测得两星中心间距
为R,其运动的角速度为ω,求两星的总质量。解:设两星球质量分别为m1和m2,
都绕连线上O点作同周期转动
又令其半径分别为R1和R2,则
返回分析与解答例4:宇航员站在一星球表面上的某高处,沿水平方向抛出一
小球,经过时间t ,小球落到星球表面,测得抛出点与
落地点之间的距离为L 。若抛出时的初速度为原来的2
倍,则抛出点与落地点之间的距离为 ,已知两落
地点在同一水平面上,该星球的半径为R ,引力常数为
G ,求该星球的质量。分析与解答返回解:在该星球表面,小球做平抛运动,则:
当初速度为v0时 X1= v0 t ①h = 1/2 g t2 ②③ 当初速度为2v0时 X2=2v0 t ④⑤又据万有引力定律 g =⑥返回练习1:两颗靠得很近的恒星称为双星,这两颗星必须各以一
定速率绕某一中心转动才不至于因万有引力作用而吸
引在一起。已知双星的质量分别为m1和m2 ,相距为
L ,求:(1)双星转动的半径。
(2)双星转动的周期。答案返回2 :3练习2:月球表面的重力加速度是地球表面重力加速度的1/6,
月球半径是地球半径的1/4,试求月球与地球的密度
之比。答案 练习3:在某星球上,宇航员用弹簧秤称得质量为m的砝码重
为F ,乘宇宙飞船靠近该星球表面空间飞行,测得其
环绕周期是T ,根据上述各量,试求该星球的质量。答案返回作业布置1:p74 2、3
2:复习 第四节
3:预习 第五节谢谢合作返回2009年3月8日福山区仪器站录制导播:孙玉师 摄像:丁世俊 隋浩
②:“距离R”是指两质点中心之间的距离,当质点是
两均质球体时,R是指两球体球心之间的距离。 万有引力理论的成就之一:计算天体的质量之二:计算天体的密度之三:发现未知天体练习一练习二练习三二:万有引力理论的成就应用之一:计算天体的质量原理:对于有卫星的天体,可以认为卫星绕天体中心 做匀速圆周运动,天体对卫星的万有引力提供卫星做匀速圆周运动的向心力。1:若已知卫星绕天体做匀速圆周运动的轨道半径为r,卫
星运动的周期为T,据牛顿第二定律例1继续例1:登月密封舱在离月球表面h处的空中沿圆形轨道运行,
周期是T,已知月球的半径是R,万有引力常数是G,
据此试计算月球的质量。分析与解答返回2:若已知卫星绕中心天体做圆周运动的轨道半径为r,卫星
运动的线速度为v,据牛顿第二定律 3:若已知卫星运动的线速度v和运行周期T,则据牛顿第二
定律4:对于没有卫星的天体(或虽有卫星,但不知道有关卫
星运动的参量),不考虑天体自转的影响,根据万有
引力等于重力的关系来计算天体的质量
----------卡文迪许在 实验室”称量”地球的质量 R----------------为天体的半径g----------------天体表面的重力加速度返回
科学真是迷人。根据零星的事实,增添一点猜想,竟能赢得那么多的收获!
--马克·吐温应用之二:计算天体的密度原理:1 利用F引=F向,先计算天体的质量M
2 再计算天体的体积 V
3 最后利用密度公式计算天体的密度情形之一:卫星在天体上空情形之二:物体在天体表面例2返回设:m卫为环绕卫星质量;r 为环绕卫星的轨道半径;T为环绕卫星的周期。返回g 为中心天体表面的重力加速度;R 为中心天体的半径返回分别应用重力等于万有引力列式求m ,再运用题目
中的比例关系对密度比例化简求解。例2:一物体在某行星表面受到的吸引力为地球表面吸引力
的a倍,该行星半径是地球半径的b倍,若该行星和地
的质量分布都是均匀的,试求该星球密度和地球密度
之比。 解答解答设地球质量为m1 ,地球半径为R,某星球质量为m2
物体的质量为m 。∵∴则:某星球与地球的密度之比返回应用之三:发现未知天体-------- 万有引力定律的贡献背景:1781年由英国物理学家威廉.赫歇尔发现了天王
星,但人们观测到的天王星的运行轨迹与万有引
力定律推测的结果有一些误差,于是人们就推测
在天王星外面轨道上还应有其它星体…… 返回1. 1845年英国人亚当斯和法国天文学家勒维耶根据计算
“发现”了海王星(第8个行星)。
1846年9月23日晚,德国的伽勒在勒维耶预言的位置发现了该星。
2:1705年英国天文学家哈雷根据万有引力定律计算了一颗著名彗星的轨道,并正确预言了它的回归。
例3例4双星问题例3:两个星球组成双星,它们在相互之间的万有引力作用下
绕连线上的某点作匀速圆周运动,现测得两星中心间距
为R,其运动的角速度为ω,求两星的总质量。解:设两星球质量分别为m1和m2,
都绕连线上O点作同周期转动
又令其半径分别为R1和R2,则
返回分析与解答例4:宇航员站在一星球表面上的某高处,沿水平方向抛出一
小球,经过时间t ,小球落到星球表面,测得抛出点与
落地点之间的距离为L 。若抛出时的初速度为原来的2
倍,则抛出点与落地点之间的距离为 ,已知两落
地点在同一水平面上,该星球的半径为R ,引力常数为
G ,求该星球的质量。分析与解答返回解:在该星球表面,小球做平抛运动,则:
当初速度为v0时 X1= v0 t ①h = 1/2 g t2 ②③ 当初速度为2v0时 X2=2v0 t ④⑤又据万有引力定律 g =⑥返回练习1:两颗靠得很近的恒星称为双星,这两颗星必须各以一
定速率绕某一中心转动才不至于因万有引力作用而吸
引在一起。已知双星的质量分别为m1和m2 ,相距为
L ,求:(1)双星转动的半径。
(2)双星转动的周期。答案返回2 :3练习2:月球表面的重力加速度是地球表面重力加速度的1/6,
月球半径是地球半径的1/4,试求月球与地球的密度
之比。答案 练习3:在某星球上,宇航员用弹簧秤称得质量为m的砝码重
为F ,乘宇宙飞船靠近该星球表面空间飞行,测得其
环绕周期是T ,根据上述各量,试求该星球的质量。答案返回作业布置1:p74 2、3
2:复习 第四节
3:预习 第五节谢谢合作返回2009年3月8日福山区仪器站录制导播:孙玉师 摄像:丁世俊 隋浩
