北京版六年级下册总复习—图形与几何(一)(课件)
文档属性
| 名称 | 北京版六年级下册总复习—图形与几何(一)(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-08 00:00:00 | ||
图片预览






文档简介
(共20张PPT)
图形与
几何(一)
北京版 小升初复习
知识要点
一、图形的认识:
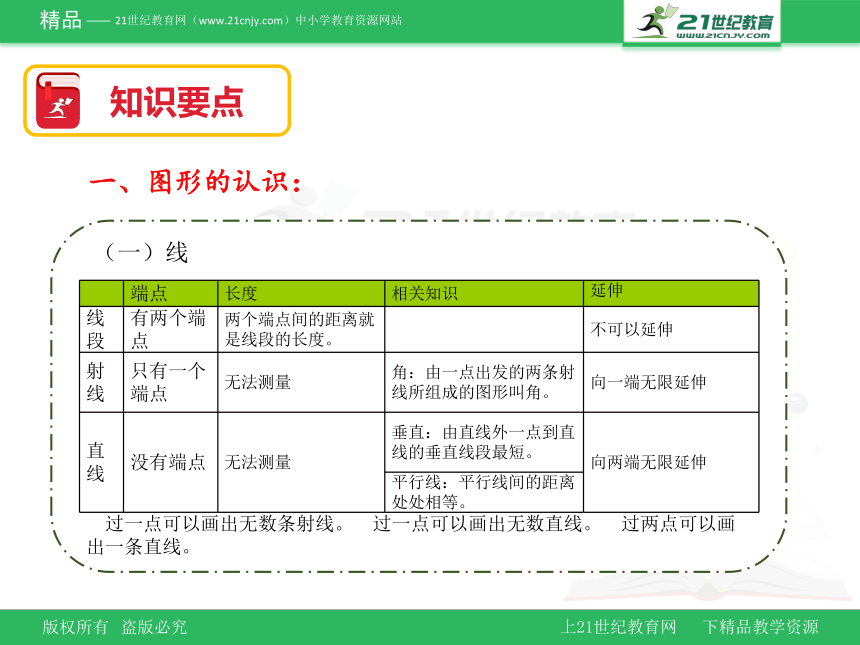
(一)线
端点 长度 相关知识 延伸
线段 有两个端点 两个端点间的距离就是线段的长度。 不可以延伸
射线 只有一个端点 无法测量 角:由一点出发的两条射线所组成的图形叫角。 向一端无限延伸
直线 没有端点 无法测量 垂直:由直线外一点到直线的垂直线段最短。 向两端无限延伸
平行线:平行线间的距离处处相等。 过一点可以画出无数条射线。 过一点可以画出无数直线。 过两点可以画出一条直线。
知识要点
一、图形的认识:
(二)角
1.定义:由一点出发的两条射线所组成的图形
2.分类:
锐角 小于90° 平角 等于180°
直角 等于90° 周角 等于360°
钝角 大于90°小于180°
典型例题
解析:
因为钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;当钟面上9时或3时整,时针指着9或3,分针指12,时针与分针之间有3个大格是90°,是直角;钟面上6时整,时针与分针之间有6个大格是180°,是平角;据此判断即可.
1.钟面上 时整,时针与分针夹角是直角,钟面上6时整,时针与分针夹角是 度角,是 角.
9或3
解:
当钟面上9时或3时整,时针指着9或3,分针指12,时针与分针之间有3个大格是90°,是直角;
钟面上6时整,时针与分针之间有6个大格是180°,是平角;
180
平
典型例题
解析:
因为线段有两个端点,射线只有一个端点,
所以由图可以看出:图中有3条线段,有6条射线.
答:图中有3条线段,有6条射线.
故此题答案为:3,6.
2.在一条直线上有A、B、C三点,如下图.图中有 条线段,有 条射线.
3
6
典型例题
解析:
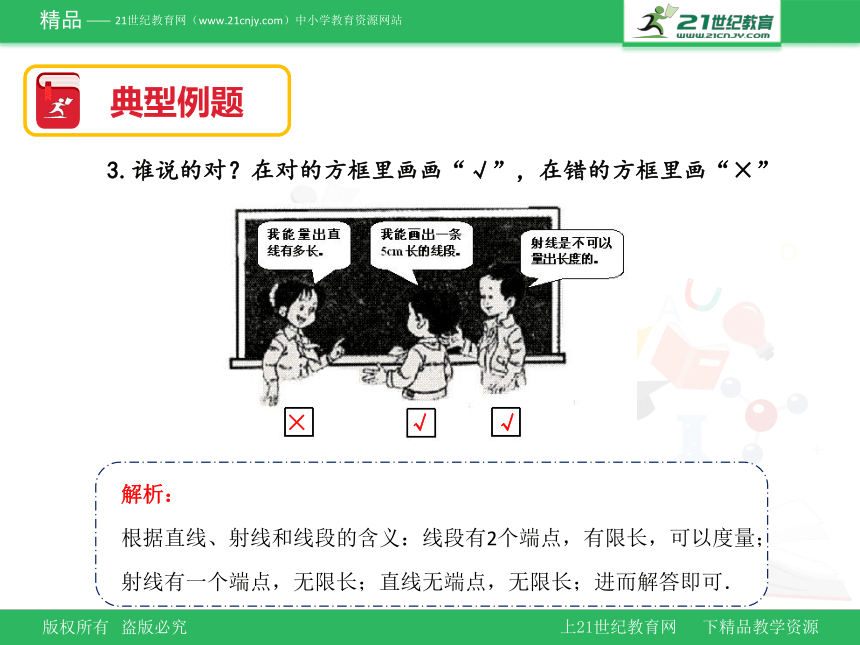
根据直线、射线和线段的含义:线段有2个端点,有限长,可以度量;射线有一个端点,无限长;直线无端点,无限长;进而解答即可.
3.谁说的对?在对的方框里画画“√”,在错的方框里画“×”
×
√
√
巩固提升
如图:一只青蛙从A到B有很多条路可走,其中走哪一条最近?长多少厘米?(单位:厘米)
解析:
因两点间线段最短,所以走直径最近.据此解答.
2+2+2=6(厘米)
答:走直径最近,长6厘米.
知识要点
二、图形的分类:
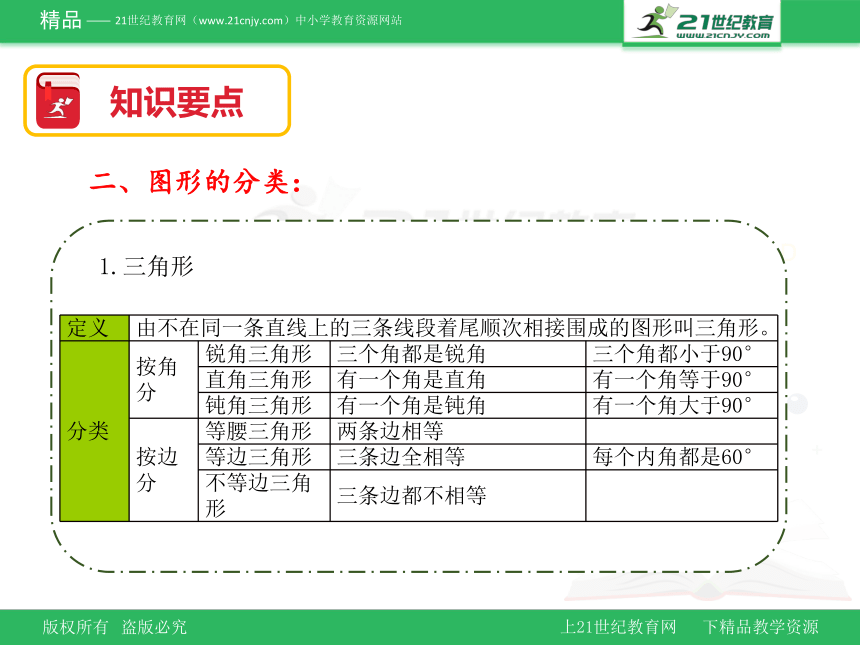
1.三角形
定义 由不在同一条直线上的三条线段着尾顺次相接围成的图形叫三角形。 分类 按角分 锐角三角形 三个角都是锐角 三个角都小于90°
直角三角形 有一个角是直角 有一个角等于90°
钝角三角形 有一个角是钝角 有一个角大于90°
按边分 等腰三角形 两条边相等
等边三角形 三条边全相等 每个内角都是60°
不等边三角形 三条边都不相等
知识要点
二、图形的分类:
1.三角形
图形及字母意义 面积公式 特征
三角形 a——底h——高 S=ah÷2面积=底高÷2 两边之和大于第三条边。两边之差小于第三条边。三个角的内角和是180°。有三条边和三个角,具有稳定性。
知识要点
二、图形的分类:
2.四边形
定义 由不在同一直线上的四条线段首尾顺次相接围成的封闭图形叫四边形 分类 平行四边形 平行四边形 两组对边分别平行且相等
长方形 两对边分别相等 四个角都是直角
正方形 四条边都相等 四个角都是直角
梯形 等腰梯形 只有一组对边平行,两条腰相等的梯形。
直角梯形 一条腰与底垂直的梯形叫做直角梯形。 有两个角是直角
知识要点
二、图形的分类:
3.圆形
图形及字母意义 面积公式 周长公式 特征
圆形 O——圆心d——直径r——半径 S=r2面积=半径2 ——圆周率 C=d=2r周长=直径周长=2半径 同一圆内所有半径、所有直径分别相等直径等于半径的2倍
典型例题
解析:
由三角形的内角和求出另外两个角的和,再根据最小的内角是51°来判断其它两个角的情况,进而根据三角形的分类判定该三角形的类别.
180°-51°=129°;另外两个角的和是129°,最小的内角是51°,
假设另外两个角中还有一个是51°,另一个就是:129°-51°=78°;
最大的内角最大只能是78°,所以这个三角形的三个角都是锐角,这个三角形一定是锐角三角形.
1.一个三角形的三个内角度数各不相等,其中最小的角是51°,那么这个三角形是一个( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
A
典型例题
解析:
依据平行四边形的意义,即两组对边分别平行的四边形,叫做平行四边形;
两根4cm的为对边,两根7cm的为对边,就可以组成平行四边形,
用长4cm,4cm,7cm,7cm的四根小棒可以围成无数个平行四边形;
2.用长4cm,4cm,7cm,7cm的四根小棒可以搭成( )形状不同的平行四边形.
A.1 B.2 C.3 D.无数
D
典型例题
解析:
三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边,
且12=3+4+5=4+4+4=2+5+5,
符合题意的三角形各边分别为:
①3、4、5;
②4、4、4;
③2、5、5;
所以共有3种剪法,可以是3、4、5;4、4、4;2、5、5.
3.把一根12厘米的吸管剪成3段(每段都是整厘米数),摆成一个三角形,共有几种剪法,你能全部列举出来吗?
巩固提升
如图,长方形的面积和圆的面积相等,已知圆的半径是3厘米,求阴影部分的周长与面积各是多少?
解析:
(1)由图意可知:阴影部分的周长=长方形的周长-圆的半径×2+圆周长× ,,圆的半径已知,从而可以求圆的周长,再据“长方形的面积和圆的面积相等”即可求出长方形的长,从而可求长方形的周长,进而求出阴影的周长;
(2)阴影部分的面积=圆面积×(1- ),将(1)中求出的数据代入此等式即可求解.
巩固提升
解:
(1)圆的周长:2×3.14×3=18.84(厘米),
圆的面积:3.14×32=28.26(平方厘米),
长方形的长:28.26÷3=9.42(厘米),
长方形的周长:(9.42+3)×2=24.84(厘米),
则阴影部分的周长:
24.84-3×2+18.84× =24.84-6+4.71,
=18.84+4.71,
=23.55(厘米);
巩固提升
(2)阴影部分的面积:
28.26×(1- )
=28.26×
=21.195(平方厘米);
答:阴影部分的周长和面积分别是23.55厘米和21.195平方厘米.
课堂小结
图形与几何复习提纲
1、直线、射线和线段的概念,理解它们的联系和区别;
2、在同一平面内,两条直线的位置关系。
3、把学过的三角形进行分类,用图表示它们之间的关系。
4、用分类和画图的方式复习四边形的知识。
5、熟记圆的各种概念和公式。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
图形与
几何(一)
北京版 小升初复习
知识要点
一、图形的认识:
(一)线
端点 长度 相关知识 延伸
线段 有两个端点 两个端点间的距离就是线段的长度。 不可以延伸
射线 只有一个端点 无法测量 角:由一点出发的两条射线所组成的图形叫角。 向一端无限延伸
直线 没有端点 无法测量 垂直:由直线外一点到直线的垂直线段最短。 向两端无限延伸
平行线:平行线间的距离处处相等。 过一点可以画出无数条射线。 过一点可以画出无数直线。 过两点可以画出一条直线。
知识要点
一、图形的认识:
(二)角
1.定义:由一点出发的两条射线所组成的图形
2.分类:
锐角 小于90° 平角 等于180°
直角 等于90° 周角 等于360°
钝角 大于90°小于180°
典型例题
解析:
因为钟面上12个数字,以表芯为旋转点,表针转一圈是360°,被12个数字平均分成12份,每一份也就是两数之间夹角是30°;当钟面上9时或3时整,时针指着9或3,分针指12,时针与分针之间有3个大格是90°,是直角;钟面上6时整,时针与分针之间有6个大格是180°,是平角;据此判断即可.
1.钟面上 时整,时针与分针夹角是直角,钟面上6时整,时针与分针夹角是 度角,是 角.
9或3
解:
当钟面上9时或3时整,时针指着9或3,分针指12,时针与分针之间有3个大格是90°,是直角;
钟面上6时整,时针与分针之间有6个大格是180°,是平角;
180
平
典型例题
解析:
因为线段有两个端点,射线只有一个端点,
所以由图可以看出:图中有3条线段,有6条射线.
答:图中有3条线段,有6条射线.
故此题答案为:3,6.
2.在一条直线上有A、B、C三点,如下图.图中有 条线段,有 条射线.
3
6
典型例题
解析:
根据直线、射线和线段的含义:线段有2个端点,有限长,可以度量;射线有一个端点,无限长;直线无端点,无限长;进而解答即可.
3.谁说的对?在对的方框里画画“√”,在错的方框里画“×”
×
√
√
巩固提升
如图:一只青蛙从A到B有很多条路可走,其中走哪一条最近?长多少厘米?(单位:厘米)
解析:
因两点间线段最短,所以走直径最近.据此解答.
2+2+2=6(厘米)
答:走直径最近,长6厘米.
知识要点
二、图形的分类:
1.三角形
定义 由不在同一条直线上的三条线段着尾顺次相接围成的图形叫三角形。 分类 按角分 锐角三角形 三个角都是锐角 三个角都小于90°
直角三角形 有一个角是直角 有一个角等于90°
钝角三角形 有一个角是钝角 有一个角大于90°
按边分 等腰三角形 两条边相等
等边三角形 三条边全相等 每个内角都是60°
不等边三角形 三条边都不相等
知识要点
二、图形的分类:
1.三角形
图形及字母意义 面积公式 特征
三角形 a——底h——高 S=ah÷2面积=底高÷2 两边之和大于第三条边。两边之差小于第三条边。三个角的内角和是180°。有三条边和三个角,具有稳定性。
知识要点
二、图形的分类:
2.四边形
定义 由不在同一直线上的四条线段首尾顺次相接围成的封闭图形叫四边形 分类 平行四边形 平行四边形 两组对边分别平行且相等
长方形 两对边分别相等 四个角都是直角
正方形 四条边都相等 四个角都是直角
梯形 等腰梯形 只有一组对边平行,两条腰相等的梯形。
直角梯形 一条腰与底垂直的梯形叫做直角梯形。 有两个角是直角
知识要点
二、图形的分类:
3.圆形
图形及字母意义 面积公式 周长公式 特征
圆形 O——圆心d——直径r——半径 S=r2面积=半径2 ——圆周率 C=d=2r周长=直径周长=2半径 同一圆内所有半径、所有直径分别相等直径等于半径的2倍
典型例题
解析:
由三角形的内角和求出另外两个角的和,再根据最小的内角是51°来判断其它两个角的情况,进而根据三角形的分类判定该三角形的类别.
180°-51°=129°;另外两个角的和是129°,最小的内角是51°,
假设另外两个角中还有一个是51°,另一个就是:129°-51°=78°;
最大的内角最大只能是78°,所以这个三角形的三个角都是锐角,这个三角形一定是锐角三角形.
1.一个三角形的三个内角度数各不相等,其中最小的角是51°,那么这个三角形是一个( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
A
典型例题
解析:
依据平行四边形的意义,即两组对边分别平行的四边形,叫做平行四边形;
两根4cm的为对边,两根7cm的为对边,就可以组成平行四边形,
用长4cm,4cm,7cm,7cm的四根小棒可以围成无数个平行四边形;
2.用长4cm,4cm,7cm,7cm的四根小棒可以搭成( )形状不同的平行四边形.
A.1 B.2 C.3 D.无数
D
典型例题
解析:
三角形的特性:两边之和大于第三边,三角形的两边的差一定小于第三边,
且12=3+4+5=4+4+4=2+5+5,
符合题意的三角形各边分别为:
①3、4、5;
②4、4、4;
③2、5、5;
所以共有3种剪法,可以是3、4、5;4、4、4;2、5、5.
3.把一根12厘米的吸管剪成3段(每段都是整厘米数),摆成一个三角形,共有几种剪法,你能全部列举出来吗?
巩固提升
如图,长方形的面积和圆的面积相等,已知圆的半径是3厘米,求阴影部分的周长与面积各是多少?
解析:
(1)由图意可知:阴影部分的周长=长方形的周长-圆的半径×2+圆周长× ,,圆的半径已知,从而可以求圆的周长,再据“长方形的面积和圆的面积相等”即可求出长方形的长,从而可求长方形的周长,进而求出阴影的周长;
(2)阴影部分的面积=圆面积×(1- ),将(1)中求出的数据代入此等式即可求解.
巩固提升
解:
(1)圆的周长:2×3.14×3=18.84(厘米),
圆的面积:3.14×32=28.26(平方厘米),
长方形的长:28.26÷3=9.42(厘米),
长方形的周长:(9.42+3)×2=24.84(厘米),
则阴影部分的周长:
24.84-3×2+18.84× =24.84-6+4.71,
=18.84+4.71,
=23.55(厘米);
巩固提升
(2)阴影部分的面积:
28.26×(1- )
=28.26×
=21.195(平方厘米);
答:阴影部分的周长和面积分别是23.55厘米和21.195平方厘米.
课堂小结
图形与几何复习提纲
1、直线、射线和线段的概念,理解它们的联系和区别;
2、在同一平面内,两条直线的位置关系。
3、把学过的三角形进行分类,用图表示它们之间的关系。
4、用分类和画图的方式复习四边形的知识。
5、熟记圆的各种概念和公式。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
