5.1.2 轴对称变换 同步练习
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
5.1.2 轴对称变换
班级:___________姓名:___________得分:__________
一.选择题
1.将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平后,你可以看到的图形是( )21·cn·jy·com
A. B.
C. D.
2.从平面镜里看到背后墙上电子钟的示数如图所示,这时的正确时间是( )
A.21:05 B.21:15 C.20:15 D.20:12
3.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF B.∠B=∠E
C.AB=DE D.AD的连线被MN垂直平分
4.如图,△ABC与△A′B′C′关于直线l对称,且∠A=105°,∠C′=30°,则∠B=( )
A.25° B.45° C.30° D.20°
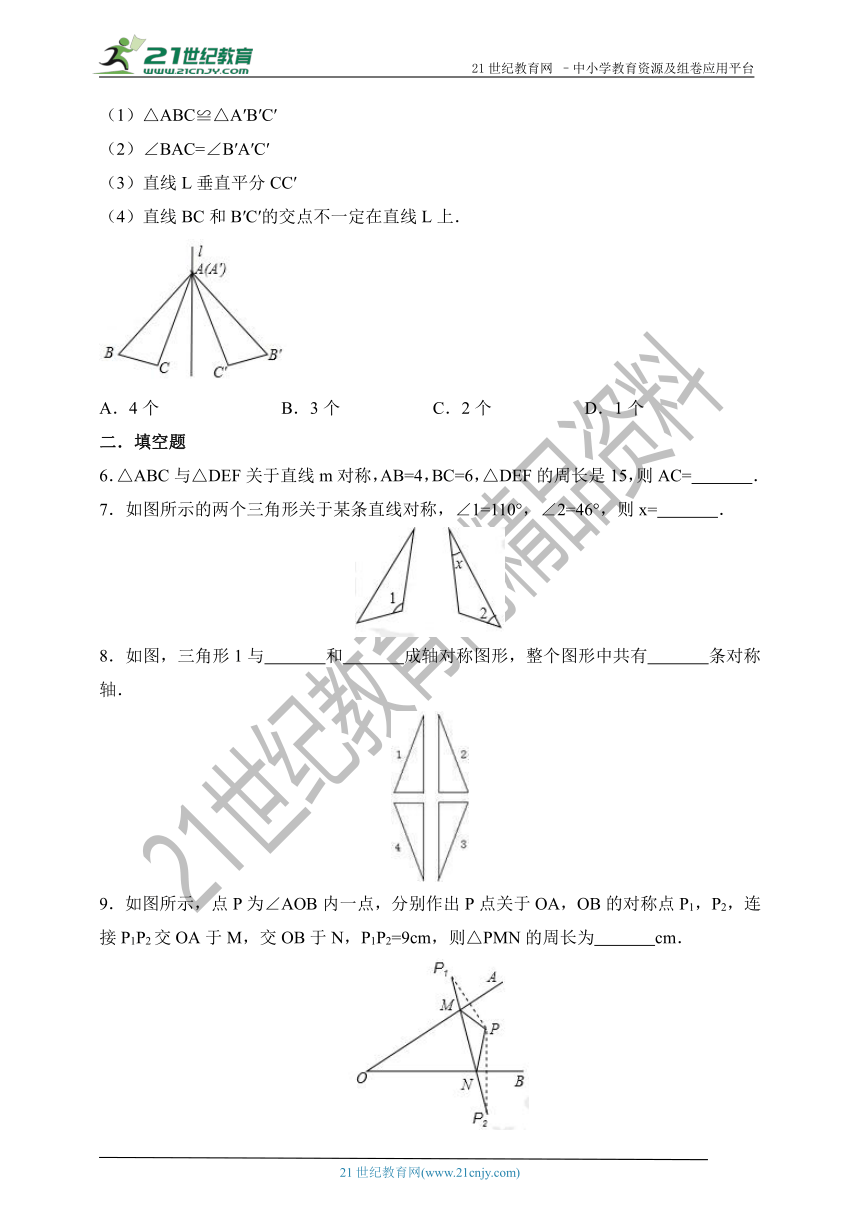
5.如图,△ABC和△A′B′C′关于直线L对称,下列结论中正确的有( )
(1)△ABC≌△A′B′C′
(2)∠BAC=∠B′A′C′
(3)直线L垂直平分CC′
(4)直线BC和B′C′的交点不一定在直线L上.
A.4个 B.3个 C.2个 D.1个
二.填空题
6.△ABC与△DEF关于直线m对称,AB=4,BC=6,△DEF的周长是15,则AC= .
7.如图所示的两个三角形关于某条直线对称,∠1=110°,∠2=46°,则x= .
8.如图,三角形1与 和 成轴对称图形,整个图形中共有 条对称轴.
9.如图所示,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=9cm,则△PMN的周长为 cm.
三.解答题
10.如图,在∠AOB外有一点P,先作点P关于直线OA的对称点P1,再作点P关于直线OB的对称点P2.21教育网
(1)试猜想∠P1OP2与∠AOB的数量关系,并加以证明;
(2)当点P在∠AOB内部时,上述结论是否成立?画图加以证明.
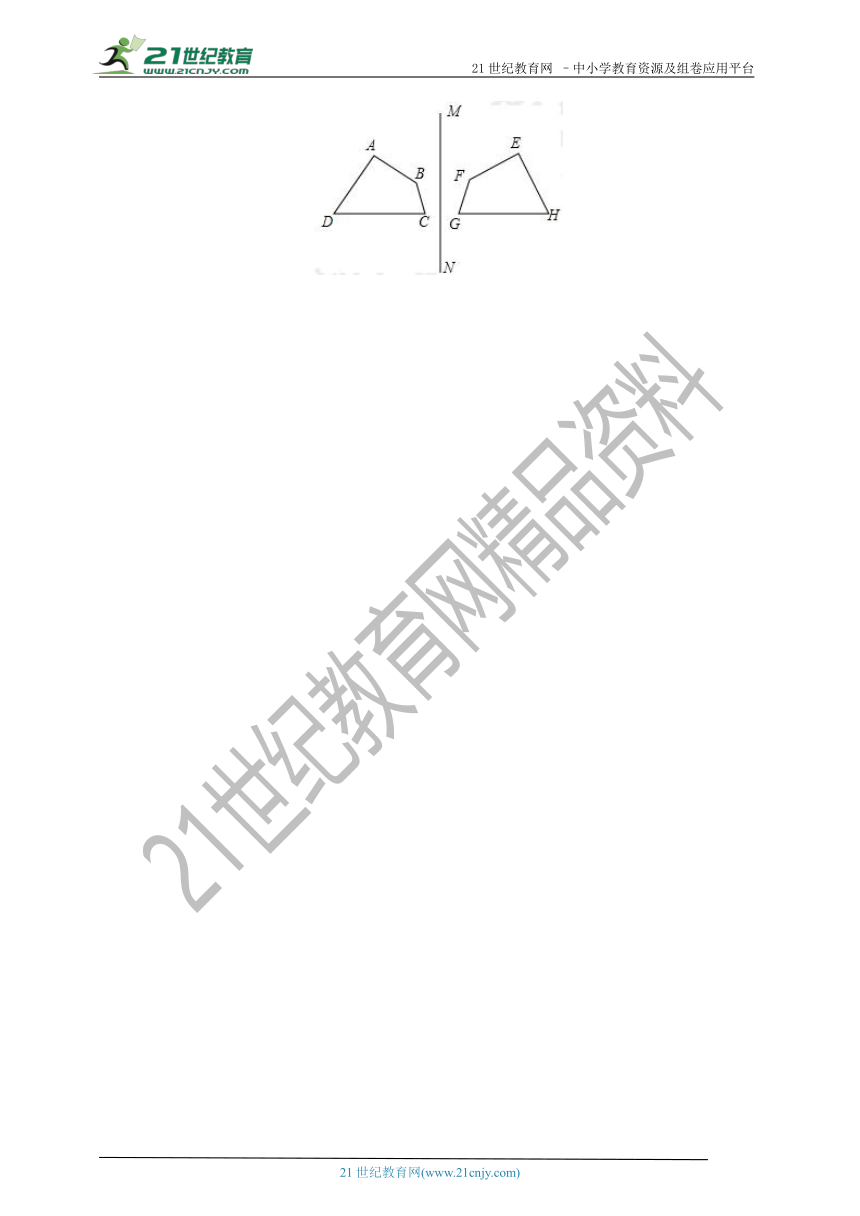
11.如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.21cnjy.com
(1)试写出EF,AD的长度;
(2)求∠G的度数;
(3)连接BF,线段BF与直线MN有什么关系?
试题解析
一.选择题
1.C
【分析】根据轴对称的知识可以解答本题.
【解答】解:由题意可得,
展开后的图形呈轴对称,
故选:C.
【点评】本题考查生活中的轴对称现象,解题的关键是明确题意,利用数形结合的思想解答.
2.A
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.
【解答】解:由图分析可得题中所给的“20:15”与“21:05”成轴对称,这时的时间应是21:05.www.21-cn-jy.com
故选:A.
【点评】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
3.A
【分析】根据轴对称的性质作答.
【解答】解:A、AB与DF不是对应线段,不一定平行,故错误;
B、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,∠B=∠E,正确;
C、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,AB=DE,正确;
D、△ABC与△DEF关于直线MN轴对称,A与D的对应点,AD的连线被MN垂直平分,正确.
故选:A.
【点评】本题主要考查了轴对称的性质:①如果两个图形关于某直线对称,那么这两个图形全等;②如果两个图形关于某直线对称,那么对应线段或者平行,或者共线,或者相交于对称轴上一点;③如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线.21世纪教育网
4.B
【分析】首先根据对称的两个图形全等求得∠C的度数,然后在△ABC中利用三角形内角和求解.
【解答】解:∠C=∠C'=30°,
则△ABC中,∠B=180°﹣105°﹣30°=45°.
故选:B.
【点评】本题考查了轴对称的性质,理解轴对称的两个图形全等是关键.
5.B
【分析】根据轴对称的性质求解.
【解答】解:(1)正确;
(2)正确;
(3)正确;
(4)“直线BC和B′C′的交点不一定在直线L上”,应是一定在直线L上的.
故选:B.
【点评】轴对称的性质:①成轴对称的两个图形是全等形;②对称轴是对应点连线的垂直平分线;③对应线段或者平行,或者重合,或者相交.如果相交,那么交点一定在对称轴上.2·1·c·n·j·y
二.填空题
6.5
【分析】首先根据成轴对称的两个三角形的周长相等确定△ABC的周长,然后减去其他两边的长即可求得第三边的长.21·世纪*教育网
【解答】解:∵△ABC与△DEF关于直线m对称,△DEF的周长是15,
∴△ABC的周长为15,
∵AB=4,BC=6,
∴AC=15﹣AB﹣BC=15﹣4﹣6=5,
故答案为:5.
【点评】本题考查了轴对称的性质,解题的关键是能够根据轴对称的性质确定三角形ABC的周长,难度不大.
7.24°
【分析】根据轴对称的性质可得∠3=∠1,再利用三角形的内角和定理列式计算即可得解.
【解答】解:∵两个三角形关于某条直线对称,
∴∠3=∠1=110°,
∴x=180°﹣∠2﹣∠3=180°﹣46°﹣110°=24°.
故答案为:24°.
【点评】本题考查了轴对称的性质,三角形的内角和定理,是基础题,熟记性质并求出∠3的度数是解题的关键.www-2-1-cnjy-com
8.与三角形1成轴对称图形是三角形2与三角形4,对称轴有2条.
【分析】根据轴对称图形的定义与判断可知.
【解答】解:与三角形1成轴对称图形是三角形2与三角形4,对称轴有2条.
【点评】本题考查轴对称图形的定义与判断,如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.
三.解答题
10.【分析】(1)利用轴对称图形的性质得出相等的角,进而得出∠P1OP2=∠3+∠4=∠1+∠2+2∠3=2∠2+2∠3=2(∠2+∠3)即可得出答案;2-1-c-n-j-y
(2)利用轴对称图形的性质得出相等的角,进而得出∠P1OP2=∠1+∠2+∠3+∠4=2(∠2+∠3)即可得出答案.21*cnjy*com
【解答】解:(1)∠P1OP2=2∠AOB,
理由:如图1,∵点P关于直线OA的对称点P1,点P关于直线OB的对称点P2,
∴∠1=∠2,∠POB=∠BOP2,则∠1+∠2+∠3=∠4,
∴∠P1OP2=∠3+∠4=∠1+∠2+2∠3=2∠2+2∠3=2(∠2+∠3)=2∠AOB;
(2))∠P1OP2=2∠AOB,
理由:如图2,∵点P关于直线OA的对称点P1,点P关于直线OB的对称点P2,
∴∠1=∠2,∠3=∠4,
∴∠P1OP2=∠1+∠2+∠3+∠4=2(∠2+∠3)=2∠AOB.
【点评】此题主要考查了轴对称图形的性质,利用对称得出相等的角是解题关键.
11.【分析】(1)根据图形写出对应线段即可;
(2)对称图形的对应角相等,据此求解;
(3)根据“对应点的连线被对称轴垂直平分”求解;
【解答】解:(1)∵四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.【21·世纪·教育·网】
∴EF=AB=3cm,AD=EH=4cm;
(2)∵∠B=125°,∠A+∠D=155°,
∴∠C=80°,
∴∠G=∠C=80°;
(3)∵对称轴垂直平分对称点的连线,
∴直线MN垂直平分BF.
【点评】本题考查了轴对称的性质,解题的关键是了解轴对称的性质,难度不大,属于基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.1.2 轴对称变换
班级:___________姓名:___________得分:__________
一.选择题
1.将一张长方形的纸片对折,然后用笔尖在上面扎出字母“B”,再把它展开铺平后,你可以看到的图形是( )21·cn·jy·com
A. B.
C. D.
2.从平面镜里看到背后墙上电子钟的示数如图所示,这时的正确时间是( )
A.21:05 B.21:15 C.20:15 D.20:12
3.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
A.AB∥DF B.∠B=∠E
C.AB=DE D.AD的连线被MN垂直平分
4.如图,△ABC与△A′B′C′关于直线l对称,且∠A=105°,∠C′=30°,则∠B=( )
A.25° B.45° C.30° D.20°
5.如图,△ABC和△A′B′C′关于直线L对称,下列结论中正确的有( )
(1)△ABC≌△A′B′C′
(2)∠BAC=∠B′A′C′
(3)直线L垂直平分CC′
(4)直线BC和B′C′的交点不一定在直线L上.
A.4个 B.3个 C.2个 D.1个
二.填空题
6.△ABC与△DEF关于直线m对称,AB=4,BC=6,△DEF的周长是15,则AC= .
7.如图所示的两个三角形关于某条直线对称,∠1=110°,∠2=46°,则x= .
8.如图,三角形1与 和 成轴对称图形,整个图形中共有 条对称轴.
9.如图所示,点P为∠AOB内一点,分别作出P点关于OA,OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,P1P2=9cm,则△PMN的周长为 cm.
三.解答题
10.如图,在∠AOB外有一点P,先作点P关于直线OA的对称点P1,再作点P关于直线OB的对称点P2.21教育网
(1)试猜想∠P1OP2与∠AOB的数量关系,并加以证明;
(2)当点P在∠AOB内部时,上述结论是否成立?画图加以证明.
11.如图,已知四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.21cnjy.com
(1)试写出EF,AD的长度;
(2)求∠G的度数;
(3)连接BF,线段BF与直线MN有什么关系?
试题解析
一.选择题
1.C
【分析】根据轴对称的知识可以解答本题.
【解答】解:由题意可得,
展开后的图形呈轴对称,
故选:C.
【点评】本题考查生活中的轴对称现象,解题的关键是明确题意,利用数形结合的思想解答.
2.A
【分析】根据镜面对称的性质,在平面镜中的像与现实中的事物恰好顺序颠倒,且关于镜面对称.
【解答】解:由图分析可得题中所给的“20:15”与“21:05”成轴对称,这时的时间应是21:05.www.21-cn-jy.com
故选:A.
【点评】本题考查镜面反射的原理与性质.解决此类题应认真观察,注意技巧.
3.A
【分析】根据轴对称的性质作答.
【解答】解:A、AB与DF不是对应线段,不一定平行,故错误;
B、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,∠B=∠E,正确;
C、△ABC与△DEF关于直线MN轴对称,则△ABC≌△DEF,AB=DE,正确;
D、△ABC与△DEF关于直线MN轴对称,A与D的对应点,AD的连线被MN垂直平分,正确.
故选:A.
【点评】本题主要考查了轴对称的性质:①如果两个图形关于某直线对称,那么这两个图形全等;②如果两个图形关于某直线对称,那么对应线段或者平行,或者共线,或者相交于对称轴上一点;③如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线.21世纪教育网
4.B
【分析】首先根据对称的两个图形全等求得∠C的度数,然后在△ABC中利用三角形内角和求解.
【解答】解:∠C=∠C'=30°,
则△ABC中,∠B=180°﹣105°﹣30°=45°.
故选:B.
【点评】本题考查了轴对称的性质,理解轴对称的两个图形全等是关键.
5.B
【分析】根据轴对称的性质求解.
【解答】解:(1)正确;
(2)正确;
(3)正确;
(4)“直线BC和B′C′的交点不一定在直线L上”,应是一定在直线L上的.
故选:B.
【点评】轴对称的性质:①成轴对称的两个图形是全等形;②对称轴是对应点连线的垂直平分线;③对应线段或者平行,或者重合,或者相交.如果相交,那么交点一定在对称轴上.2·1·c·n·j·y
二.填空题
6.5
【分析】首先根据成轴对称的两个三角形的周长相等确定△ABC的周长,然后减去其他两边的长即可求得第三边的长.21·世纪*教育网
【解答】解:∵△ABC与△DEF关于直线m对称,△DEF的周长是15,
∴△ABC的周长为15,
∵AB=4,BC=6,
∴AC=15﹣AB﹣BC=15﹣4﹣6=5,
故答案为:5.
【点评】本题考查了轴对称的性质,解题的关键是能够根据轴对称的性质确定三角形ABC的周长,难度不大.
7.24°
【分析】根据轴对称的性质可得∠3=∠1,再利用三角形的内角和定理列式计算即可得解.
【解答】解:∵两个三角形关于某条直线对称,
∴∠3=∠1=110°,
∴x=180°﹣∠2﹣∠3=180°﹣46°﹣110°=24°.
故答案为:24°.
【点评】本题考查了轴对称的性质,三角形的内角和定理,是基础题,熟记性质并求出∠3的度数是解题的关键.www-2-1-cnjy-com
8.与三角形1成轴对称图形是三角形2与三角形4,对称轴有2条.
【分析】根据轴对称图形的定义与判断可知.
【解答】解:与三角形1成轴对称图形是三角形2与三角形4,对称轴有2条.
【点评】本题考查轴对称图形的定义与判断,如果一个图形沿着一条直线对折,两侧的图形能完全重合,这个图形就是轴对称图形.折痕所在的这条直线叫做对称轴.
三.解答题
10.【分析】(1)利用轴对称图形的性质得出相等的角,进而得出∠P1OP2=∠3+∠4=∠1+∠2+2∠3=2∠2+2∠3=2(∠2+∠3)即可得出答案;2-1-c-n-j-y
(2)利用轴对称图形的性质得出相等的角,进而得出∠P1OP2=∠1+∠2+∠3+∠4=2(∠2+∠3)即可得出答案.21*cnjy*com
【解答】解:(1)∠P1OP2=2∠AOB,
理由:如图1,∵点P关于直线OA的对称点P1,点P关于直线OB的对称点P2,
∴∠1=∠2,∠POB=∠BOP2,则∠1+∠2+∠3=∠4,
∴∠P1OP2=∠3+∠4=∠1+∠2+2∠3=2∠2+2∠3=2(∠2+∠3)=2∠AOB;
(2))∠P1OP2=2∠AOB,
理由:如图2,∵点P关于直线OA的对称点P1,点P关于直线OB的对称点P2,
∴∠1=∠2,∠3=∠4,
∴∠P1OP2=∠1+∠2+∠3+∠4=2(∠2+∠3)=2∠AOB.
【点评】此题主要考查了轴对称图形的性质,利用对称得出相等的角是解题关键.
11.【分析】(1)根据图形写出对应线段即可;
(2)对称图形的对应角相等,据此求解;
(3)根据“对应点的连线被对称轴垂直平分”求解;
【解答】解:(1)∵四边形ABCD与四边形EFGH关于直线MN对称,∠B=125°,∠A+∠D=155°,AB=3cm,EH=4cm.【21·世纪·教育·网】
∴EF=AB=3cm,AD=EH=4cm;
(2)∵∠B=125°,∠A+∠D=155°,
∴∠C=80°,
∴∠G=∠C=80°;
(3)∵对称轴垂直平分对称点的连线,
∴直线MN垂直平分BF.
【点评】本题考查了轴对称的性质,解题的关键是了解轴对称的性质,难度不大,属于基础题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
