苏教版小学六年级数学下 6 成正比例的量(1)课件 (共17张PPT)
文档属性
| 名称 | 苏教版小学六年级数学下 6 成正比例的量(1)课件 (共17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-08 00:00:00 | ||
图片预览





文档简介
课件17张PPT。第六单元 正比例和反比例6.1 成正比例的量(1)教材第56~57页课题引入说出下列每组数量之间的关系。
(1)速度、时间、路程。
(2)单价、数量、总价。
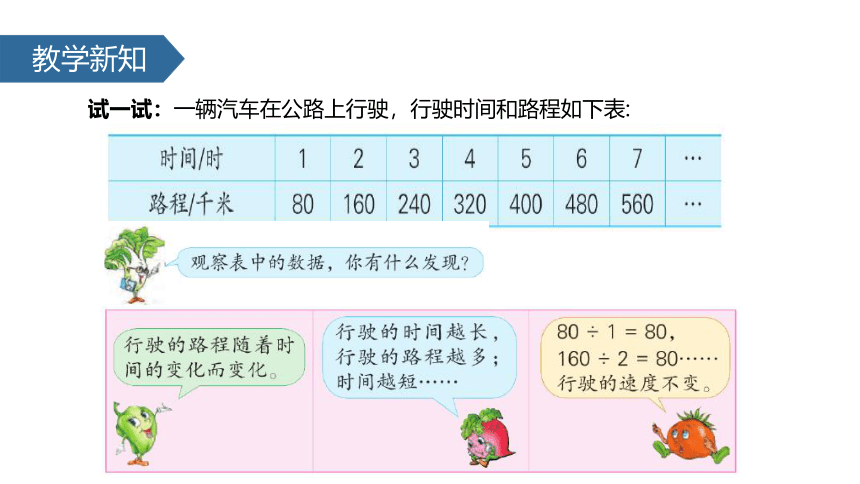
(3)工作效率、工作时间、工作总量。教学新知试一试:一辆汽车在公路上行驶,行驶时间和路程如下表:教学新知80240380320480【讲解】路程和时间是两种相关联的量,路程随着时间的变化而变化。时间扩大,路程也扩大;时间缩小,路程也缩小。
路程和时间比的比值总是一定的。因为路程和时间对应数值比的比值都是80。
教学新知结论:我们可以用下面的式子表示这几个量之间的关系:
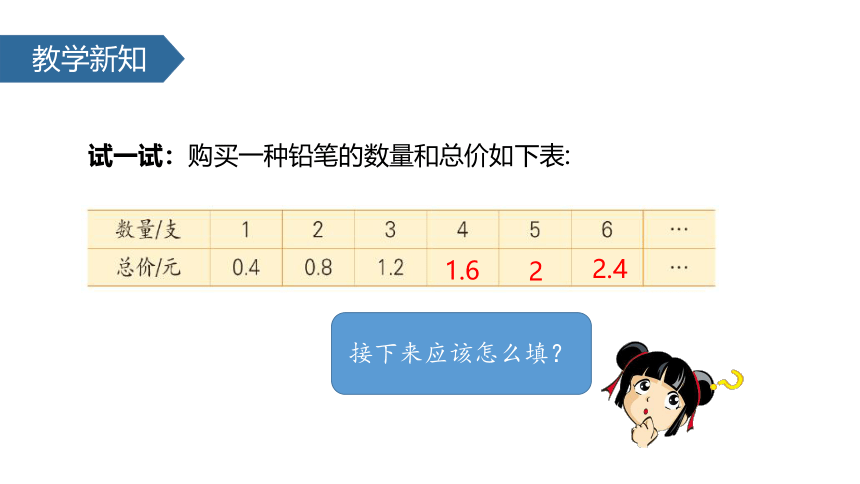
路程和时间是两种相关联的量,时间变化,路程也随着变化。当路程和相对应时间的比的比值总是一定(也就是速度一定)时,我们就说,行驶的路程和时间成正比例关系,行驶的路程和时间是成正比例的量。教学新知试一试:购买一种铅笔的数量和总价如下表:接下来应该怎么填?1.622.4教学新知?知识要点 如果用x和y表示两种相关联的量,用k表示它们的比值
正比例关系可以用下面的式子表示:? = k根据上面的例子,我们发现有以下的共同点:
①都有两种相关联的量;
②都是一种量随着另一种量变化;
③两种量里对应数值的比的比值一定。【例】一列火车1小时行驶90千米,2小时行驶180千米,3小时行驶
270千米,4小时行驶360千米,5小时行驶450千米,6小时行驶
540千米,7小时行驶630千米,8小时行驶720千米……教学新知填表:一列火车行驶的时间和路程教学新知一列火车行驶的时间和路程【方法小结】要判断两种量是否成正比例关系,首先看这两种量是否相关联,即其中一个量变化,另一个量也随着变化;其次要看相对应两个量的比值是否一定,具备以上两个条件,这两种量就成正比例。课堂练习1.填空。
(1)两种 的量,—种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的 一定,这两种量就叫做成正比
例的量,它们的关系叫做 。
(2)正比例关系用公式表示为 。
(3)观察下面的图表,回答问题: 上表中______和______是两种相关联的量,_______随着 的变化而变化的, —定,时间和米数是 的量。相关联
比值正比例关系?米数时间米数时间 每小时加工米数成正比例课堂练习2.判断下面各题中的两种量是不是成正比例关系,并说理。
(1)长方形的长一定,宽和面积。
(2)总路程一定,已经行了的路程和剩下的路程。
(3)人的身高和体重。
(4)圆柱的侧面积和高。
(5)正方形的边长和面积。
是,宽和面积的比值一定。不是,它们的比值不一定,是和一定。不成正比例,它们的比值不一定。不成正比例,它们的比值不一定。不成正比例,它们的比值不一定。课后习题1.判断下面各题中的两种量是不是成正比例关系,并说理。
(1)白糖单价一定,白糖数量和总价;
(2)稻谷的出米率一定,碾成大米重量和稻谷重量;
(3)一个人的身高和体重;
(4)长方形的长一定,宽和面积;
(5)长方形的面积一定,长和宽。成,因为总价和数量的比值单价总是一定。成,因为碾成大米重量和稻谷重量的比值总是一定。不成,因为身高与体重的比值不一定。成,因为长方形面积与宽的比值总是一定。不成正比例,长和宽的乘积一定,不是比值一定。课后习题2.填空。
(1)两种相关联的量,一种量变化,另一种量( )。
当两种量相对应的比的( )一定时,这两种量成正
比例关系。
(2)如果用字母x和y分别表示两种相关联的量,用k表示它
们的比值,正比例关系可以表示为( )。也随着变化比值?课后习题3.判断下面每题中的两个量是否成正比例,成正比例的在括号
里画“√”。
(1)每天的用煤量一定,用煤的天数和用煤的总量。 ( )
(2)圆的直径和周长。 ( )
(3)长方形的长一定,长方形的宽和周长。 ( )√√×课后习题4.《小学科技报》的份数和钱数如下表。(1)写出几组对应的钱数和份数的比,并求出比值。
26÷1=26,52÷2=26, 78÷3=26, 104÷4=26……
(2)这个比值表示的意义是什么?
这个比值表示《小学科技报》的单价。
(3)订阅的钱数和份数成正比例吗?为什么?
订阅的钱数和份数成正比例,因为它们的比值相等。课后习题5.先填出下面每个正方形的面积,再判断正方形的边长和面积是否成正
比例。6.三角形的底一定,三角形的面积和高成正比例吗?为什么?正方形的边长和面积不成正比例,因为它们的比值不一定。1 4 9 16 25成正比例,因为三角形的面积和高的比值是三角形底的2倍,而三角形的底是一定的。
(1)速度、时间、路程。
(2)单价、数量、总价。
(3)工作效率、工作时间、工作总量。教学新知试一试:一辆汽车在公路上行驶,行驶时间和路程如下表:教学新知80240380320480【讲解】路程和时间是两种相关联的量,路程随着时间的变化而变化。时间扩大,路程也扩大;时间缩小,路程也缩小。
路程和时间比的比值总是一定的。因为路程和时间对应数值比的比值都是80。
教学新知结论:我们可以用下面的式子表示这几个量之间的关系:
路程和时间是两种相关联的量,时间变化,路程也随着变化。当路程和相对应时间的比的比值总是一定(也就是速度一定)时,我们就说,行驶的路程和时间成正比例关系,行驶的路程和时间是成正比例的量。教学新知试一试:购买一种铅笔的数量和总价如下表:接下来应该怎么填?1.622.4教学新知?知识要点 如果用x和y表示两种相关联的量,用k表示它们的比值
正比例关系可以用下面的式子表示:? = k根据上面的例子,我们发现有以下的共同点:
①都有两种相关联的量;
②都是一种量随着另一种量变化;
③两种量里对应数值的比的比值一定。【例】一列火车1小时行驶90千米,2小时行驶180千米,3小时行驶
270千米,4小时行驶360千米,5小时行驶450千米,6小时行驶
540千米,7小时行驶630千米,8小时行驶720千米……教学新知填表:一列火车行驶的时间和路程教学新知一列火车行驶的时间和路程【方法小结】要判断两种量是否成正比例关系,首先看这两种量是否相关联,即其中一个量变化,另一个量也随着变化;其次要看相对应两个量的比值是否一定,具备以上两个条件,这两种量就成正比例。课堂练习1.填空。
(1)两种 的量,—种量变化,另一种量也随着变化,如果这两种
量中相对应的两个数的 一定,这两种量就叫做成正比
例的量,它们的关系叫做 。
(2)正比例关系用公式表示为 。
(3)观察下面的图表,回答问题: 上表中______和______是两种相关联的量,_______随着 的变化而变化的, —定,时间和米数是 的量。相关联
比值正比例关系?米数时间米数时间 每小时加工米数成正比例课堂练习2.判断下面各题中的两种量是不是成正比例关系,并说理。
(1)长方形的长一定,宽和面积。
(2)总路程一定,已经行了的路程和剩下的路程。
(3)人的身高和体重。
(4)圆柱的侧面积和高。
(5)正方形的边长和面积。
是,宽和面积的比值一定。不是,它们的比值不一定,是和一定。不成正比例,它们的比值不一定。不成正比例,它们的比值不一定。不成正比例,它们的比值不一定。课后习题1.判断下面各题中的两种量是不是成正比例关系,并说理。
(1)白糖单价一定,白糖数量和总价;
(2)稻谷的出米率一定,碾成大米重量和稻谷重量;
(3)一个人的身高和体重;
(4)长方形的长一定,宽和面积;
(5)长方形的面积一定,长和宽。成,因为总价和数量的比值单价总是一定。成,因为碾成大米重量和稻谷重量的比值总是一定。不成,因为身高与体重的比值不一定。成,因为长方形面积与宽的比值总是一定。不成正比例,长和宽的乘积一定,不是比值一定。课后习题2.填空。
(1)两种相关联的量,一种量变化,另一种量( )。
当两种量相对应的比的( )一定时,这两种量成正
比例关系。
(2)如果用字母x和y分别表示两种相关联的量,用k表示它
们的比值,正比例关系可以表示为( )。也随着变化比值?课后习题3.判断下面每题中的两个量是否成正比例,成正比例的在括号
里画“√”。
(1)每天的用煤量一定,用煤的天数和用煤的总量。 ( )
(2)圆的直径和周长。 ( )
(3)长方形的长一定,长方形的宽和周长。 ( )√√×课后习题4.《小学科技报》的份数和钱数如下表。(1)写出几组对应的钱数和份数的比,并求出比值。
26÷1=26,52÷2=26, 78÷3=26, 104÷4=26……
(2)这个比值表示的意义是什么?
这个比值表示《小学科技报》的单价。
(3)订阅的钱数和份数成正比例吗?为什么?
订阅的钱数和份数成正比例,因为它们的比值相等。课后习题5.先填出下面每个正方形的面积,再判断正方形的边长和面积是否成正
比例。6.三角形的底一定,三角形的面积和高成正比例吗?为什么?正方形的边长和面积不成正比例,因为它们的比值不一定。1 4 9 16 25成正比例,因为三角形的面积和高的比值是三角形底的2倍,而三角形的底是一定的。
