数学五年级上北京版5.2方程课件 (共31张)
文档属性
| 名称 | 数学五年级上北京版5.2方程课件 (共31张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-09 07:58:25 | ||
图片预览







文档简介
(共31张PPT)
第4单元 总复习
1.3 方程
学习目标
3.会利用方程解决生活中的实际问题。
1.理解用字母表示数的作用和等式的性质,体会用字母表示数的简洁性。
2.加深对方程、方程的解及解方程的区别、方程与等式的关系的理解。
情景导入
同学们,谈一谈你对方程这部分内容的认识。
CCTV
UFO
SOS
NBA
cm
探究新知
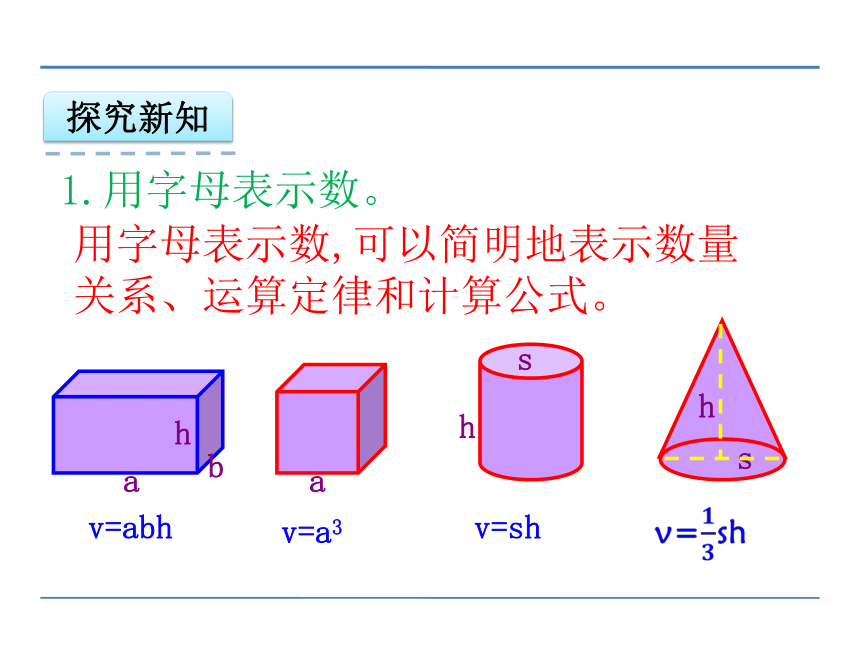
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
在含有字母的式子里,数字和字母、字母和字母中间的乘号可以记作“·”,也可以省略不写。在省略乘号的时候,要把数字写在字母的前面。
1与任何字母相乘时,1可以省略不写。两个相同字母相乘时,可以写作这个字母的平方。
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
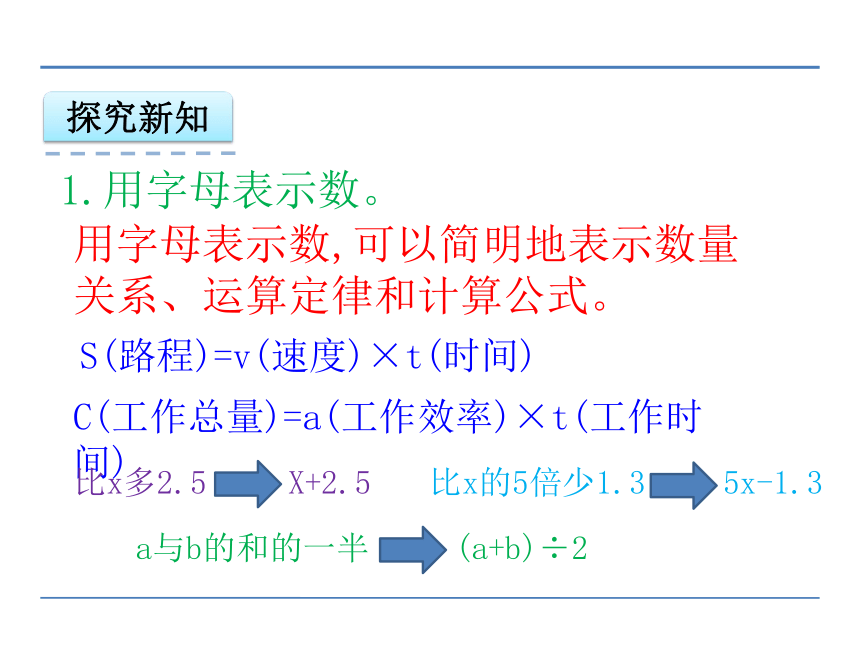
S(路程)=v(速度)×t(时间)
C(工作总量)=a(工作效率)×t(工作时间)
比x多2.5
X+2.5
比x的5倍少1.3
5x-1.3
a与b的和的一半
(a+b)÷2
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷ (b×c)
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
a
a
b
a
h
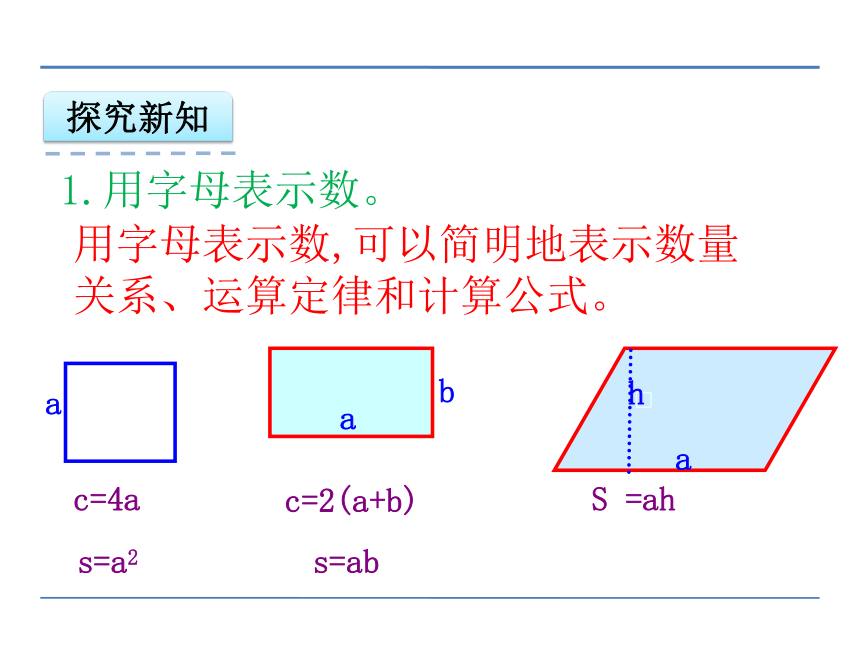
c=4a
S =ah
s=ab
s=a2
c=2(a+b)
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
a
h
b
a
h
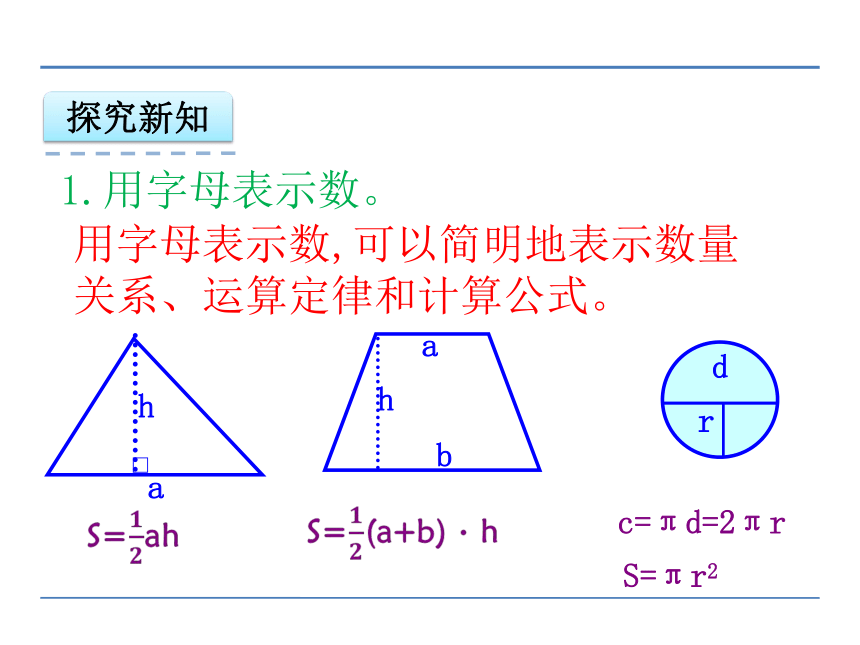
c=πd=2πr
S=πr2
d
r
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
v=abh
v=a3
v=sh
a
b
h
a
h
s
s
h
探究新知
2.将数值代入字母求值。
把具体的数代入式子求值时,书写格式:
先写出字母等于几,再写出含有字母的式子,并把数代入式子求值。
字母表示的是数,后面不写单位名称。
同一个式子,式子中所含字母取不同的数值,那么所求出的式子的值也不相同。
当a=45,b=6 时
9a+58b=9×45+58×6
=753
探究新知
方程:含有未知数的等式叫作方程。
方程的解:使方程左右两边相等的未知数的值,叫作方程的解。
解方程:求方程的解的过程叫作解方程。
方程与等式的关系:
方程一定是等式,等式不一定是方程。
3.认识方程。
4x+5不是方程,X=5是方程
探究新知
4.解方程。
等式的两边乘或除(0除外)同一个数(或式子),结果仍相等。
等式的两边加或减同一个数(或式子),结果仍相等。
a=b
a+c=b+c
a=b
a-c=b-c
a=b
a×c=b×c
a=b
a÷c=b÷c
探究新知
4.解方程。
3X+6X=7
9X÷9=7 ÷9
解:
9X=7
乘法分配律
等式两边同时除以同一个不为0的数,等式仍然成立。
探究新知
5.列方程解决实际问题。
列方程解应用题,就是用字母代替应用题中的未知量,根据数量间的相等关系列方程、解方程,进而求出未知量。
列方程解答应用题的步骤:①弄清题意,找出未知量设未知数为x 。②找出具体的数量,列出等量关系式。③根据等量关系式,列出方程。④解方程。⑤检查或验算,给出答案。
典题精讲
解方程。3x-6=6.6
思路分析:
方法一:等式的性质
方法二:被减数=减数+差
一个因数
另一个因数
积
=
÷
典题精讲
解方程。3x-6=6.6
解答:
3x-6=6.6
3x=6.6+6
3x=12.6
x=12.6÷3
x=4.2
检验:把x=4.2代入原方程。
左边=3×4.2- 6=6.6
右边=6.6
左边=右边
所以x=4.2是原方程的解。
典题精讲
A、B两地相距120千米,甲、乙两人骑自行车同时从两地相向而行,甲每时行14千米,经过4时与乙相遇,乙每时行多少千米
思路分析:
A
B
甲
乙
甲行的路程+乙行的路程=120千米
14×4
设乙每时行x千米
4x
典题精讲
A、B两地相距120千米,甲、乙两人骑自行车同时从两地相向而行,甲每时行14千米,经过4时与乙相遇,乙每时行多少千米
解答:
解:设乙每时行x千米。
14×4+4x=120
x=16
答:乙每时行16千米。
易错提醒
六年级男生比女生少40人,六年级女生人数相当于男生人数的140%,六年级男生有多少人?
解:设女生有x人,男生就有140% x人。
140% x - x = 40
0.4 x = 40
x = 100
140% x = 100 × 1.4 = 140
答:男生有140人。
错误解答
易错提醒
六年级男生比女生少40人,六年级女生人数相当于男生人数的140%,六年级男生有多少人?
根据“六年级女生人数相当于男生人数的140%”,可以把男生人数看作单位“1”的量,设男生人数为x人,女生人数就是140%x人,再根据“六年级男生比女生少40人”,可以得出数量关系式:“女生人数 – 男生人数 = 40”,根据此数量关系式列出方程。
易错提醒
六年级男生比女生少40人,六年级女生人数相当于男生人数的140%,六年级男生有多少人?
解:设男生有x人,女生就有140% x人。
140% x - x = 40
0.4 x = 40
x = 100
答:男生有100人。
正确解答
学以致用
1.填空。
(1)学校原有图书8140本,又买来a本,现在学校共有图书( )本。
(2)甲汽车运货a吨,乙汽车运货b吨,两辆汽车共运货( )吨。
(3)某人每小时行a千米,5小时行( )千米,7小时行( )千米,行S千米要( )小时。
(4)铅笔每支a元,练习本每本b元,小红买了8支铅笔和5本练习本,一共付( )元。
8a+5b
7a
s÷a
5a
a+b
8140+a
学以致用
2.判断下列式子哪些是方程。
x+8
2×6+10=22
18-2x
3x+5>20
4+0.7 x =102
x-0.25=
=30%
√
×
√
×
×
×
√
√
学以致用
3.解方程。
x-0.25=
=30%
4+0.7 x = 102
解:
解:
解:
解:
学以致用
4.金桥镇去年植树3600棵,是今年植树棵数的80﹪ ,今年植树多少棵?
解:设今年植树x棵。
80%x=3600
x=3600÷80%
x=4500
经检验x=4500是原方程的解。
答:今年植树4500棵。
解答:
学以致用
5. “国庆”商场促销,一套西服打八五折出售是1020元,这套西服原价多少元?
解答:
解:设这套西服原价x元。
x × 85% = 1020
x = 1020 ÷ 85%
x = 1200
答:这套西服原价1200元。
学以致用
6.松鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连几天采了112个松子,平均每天采14个。这几天当中有几天是雨天
思路分析:
一共采了112÷14=8(天)
设有x天是雨天,晴天是(8-x)天
晴天采摘
的松子数
+
雨天采摘的松子数
=112
学以致用
6.松鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连几天采了112个松子,平均每天采14个。这几天当中有几天是雨天
解答:
112÷14=8(天)
设这几天当中有x天是雨天,则有(8-x)天是晴天。
(8-x)×20+12x=112
x=6
答:这几天当中有6天是雨天。
学以致用
7.水果批发部要运进一批水果,第一次运进总量的22%,第二次运进1.5吨,两次共运进这批水果的62%,这批水果一共有多少吨?
解答:
设这批水果一共有x吨。
62%x - 22%x=1.5
40%x=1.5
x=3.75
答:这批水果一共有3.75吨。
课堂小结
通过这节课的学习,你学会了什么?
会用字母表示数。
会用方程表示简单情境的等量关系。
会用等式的性质解简易的方程。
运用方程解决实际问题。
谢谢
第4单元 总复习
1.3 方程
学习目标
3.会利用方程解决生活中的实际问题。
1.理解用字母表示数的作用和等式的性质,体会用字母表示数的简洁性。
2.加深对方程、方程的解及解方程的区别、方程与等式的关系的理解。
情景导入
同学们,谈一谈你对方程这部分内容的认识。
CCTV
UFO
SOS
NBA
cm
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
在含有字母的式子里,数字和字母、字母和字母中间的乘号可以记作“·”,也可以省略不写。在省略乘号的时候,要把数字写在字母的前面。
1与任何字母相乘时,1可以省略不写。两个相同字母相乘时,可以写作这个字母的平方。
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
S(路程)=v(速度)×t(时间)
C(工作总量)=a(工作效率)×t(工作时间)
比x多2.5
X+2.5
比x的5倍少1.3
5x-1.3
a与b的和的一半
(a+b)÷2
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
加法交换律:a+b=b+a
加法结合律:a+(b+c)=(a+b)+c
乘法交换律:ab=ba
乘法结合律:a(bc)=(ab)c
乘法分配律:a(b+c)=ab+ac
减法的性质:a-b-c=a-(b+c)
除法的性质:a÷b÷c=a÷ (b×c)
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
a
a
b
a
h
c=4a
S =ah
s=ab
s=a2
c=2(a+b)
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
a
h
b
a
h
c=πd=2πr
S=πr2
d
r
探究新知
1.用字母表示数。
用字母表示数,可以简明地表示数量关系、运算定律和计算公式。
v=abh
v=a3
v=sh
a
b
h
a
h
s
s
h
探究新知
2.将数值代入字母求值。
把具体的数代入式子求值时,书写格式:
先写出字母等于几,再写出含有字母的式子,并把数代入式子求值。
字母表示的是数,后面不写单位名称。
同一个式子,式子中所含字母取不同的数值,那么所求出的式子的值也不相同。
当a=45,b=6 时
9a+58b=9×45+58×6
=753
探究新知
方程:含有未知数的等式叫作方程。
方程的解:使方程左右两边相等的未知数的值,叫作方程的解。
解方程:求方程的解的过程叫作解方程。
方程与等式的关系:
方程一定是等式,等式不一定是方程。
3.认识方程。
4x+5不是方程,X=5是方程
探究新知
4.解方程。
等式的两边乘或除(0除外)同一个数(或式子),结果仍相等。
等式的两边加或减同一个数(或式子),结果仍相等。
a=b
a+c=b+c
a=b
a-c=b-c
a=b
a×c=b×c
a=b
a÷c=b÷c
探究新知
4.解方程。
3X+6X=7
9X÷9=7 ÷9
解:
9X=7
乘法分配律
等式两边同时除以同一个不为0的数,等式仍然成立。
探究新知
5.列方程解决实际问题。
列方程解应用题,就是用字母代替应用题中的未知量,根据数量间的相等关系列方程、解方程,进而求出未知量。
列方程解答应用题的步骤:①弄清题意,找出未知量设未知数为x 。②找出具体的数量,列出等量关系式。③根据等量关系式,列出方程。④解方程。⑤检查或验算,给出答案。
典题精讲
解方程。3x-6=6.6
思路分析:
方法一:等式的性质
方法二:被减数=减数+差
一个因数
另一个因数
积
=
÷
典题精讲
解方程。3x-6=6.6
解答:
3x-6=6.6
3x=6.6+6
3x=12.6
x=12.6÷3
x=4.2
检验:把x=4.2代入原方程。
左边=3×4.2- 6=6.6
右边=6.6
左边=右边
所以x=4.2是原方程的解。
典题精讲
A、B两地相距120千米,甲、乙两人骑自行车同时从两地相向而行,甲每时行14千米,经过4时与乙相遇,乙每时行多少千米
思路分析:
A
B
甲
乙
甲行的路程+乙行的路程=120千米
14×4
设乙每时行x千米
4x
典题精讲
A、B两地相距120千米,甲、乙两人骑自行车同时从两地相向而行,甲每时行14千米,经过4时与乙相遇,乙每时行多少千米
解答:
解:设乙每时行x千米。
14×4+4x=120
x=16
答:乙每时行16千米。
易错提醒
六年级男生比女生少40人,六年级女生人数相当于男生人数的140%,六年级男生有多少人?
解:设女生有x人,男生就有140% x人。
140% x - x = 40
0.4 x = 40
x = 100
140% x = 100 × 1.4 = 140
答:男生有140人。
错误解答
易错提醒
六年级男生比女生少40人,六年级女生人数相当于男生人数的140%,六年级男生有多少人?
根据“六年级女生人数相当于男生人数的140%”,可以把男生人数看作单位“1”的量,设男生人数为x人,女生人数就是140%x人,再根据“六年级男生比女生少40人”,可以得出数量关系式:“女生人数 – 男生人数 = 40”,根据此数量关系式列出方程。
易错提醒
六年级男生比女生少40人,六年级女生人数相当于男生人数的140%,六年级男生有多少人?
解:设男生有x人,女生就有140% x人。
140% x - x = 40
0.4 x = 40
x = 100
答:男生有100人。
正确解答
学以致用
1.填空。
(1)学校原有图书8140本,又买来a本,现在学校共有图书( )本。
(2)甲汽车运货a吨,乙汽车运货b吨,两辆汽车共运货( )吨。
(3)某人每小时行a千米,5小时行( )千米,7小时行( )千米,行S千米要( )小时。
(4)铅笔每支a元,练习本每本b元,小红买了8支铅笔和5本练习本,一共付( )元。
8a+5b
7a
s÷a
5a
a+b
8140+a
学以致用
2.判断下列式子哪些是方程。
x+8
2×6+10=22
18-2x
3x+5>20
4+0.7 x =102
x-0.25=
=30%
√
×
√
×
×
×
√
√
学以致用
3.解方程。
x-0.25=
=30%
4+0.7 x = 102
解:
解:
解:
解:
学以致用
4.金桥镇去年植树3600棵,是今年植树棵数的80﹪ ,今年植树多少棵?
解:设今年植树x棵。
80%x=3600
x=3600÷80%
x=4500
经检验x=4500是原方程的解。
答:今年植树4500棵。
解答:
学以致用
5. “国庆”商场促销,一套西服打八五折出售是1020元,这套西服原价多少元?
解答:
解:设这套西服原价x元。
x × 85% = 1020
x = 1020 ÷ 85%
x = 1200
答:这套西服原价1200元。
学以致用
6.松鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连几天采了112个松子,平均每天采14个。这几天当中有几天是雨天
思路分析:
一共采了112÷14=8(天)
设有x天是雨天,晴天是(8-x)天
晴天采摘
的松子数
+
雨天采摘的松子数
=112
学以致用
6.松鼠妈妈采松子,晴天每天可以采20个,雨天每天只能采12个,它一连几天采了112个松子,平均每天采14个。这几天当中有几天是雨天
解答:
112÷14=8(天)
设这几天当中有x天是雨天,则有(8-x)天是晴天。
(8-x)×20+12x=112
x=6
答:这几天当中有6天是雨天。
学以致用
7.水果批发部要运进一批水果,第一次运进总量的22%,第二次运进1.5吨,两次共运进这批水果的62%,这批水果一共有多少吨?
解答:
设这批水果一共有x吨。
62%x - 22%x=1.5
40%x=1.5
x=3.75
答:这批水果一共有3.75吨。
课堂小结
通过这节课的学习,你学会了什么?
会用字母表示数。
会用方程表示简单情境的等量关系。
会用等式的性质解简易的方程。
运用方程解决实际问题。
谢谢
