北京版小学五年级数学下 6 数学百花园 (共23张PPT)
文档属性
| 名称 | 北京版小学五年级数学下 6 数学百花园 (共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-09 09:44:02 | ||
图片预览








文档简介
课件23张PPT。第6单元 数学百花园 数学百花园学习目标1.掌握计算立体图形表面积的方法。综合运用有关知识,解决有关求物体表面积的问题,发展空间观念。2. 能够运用剪纸活动中发现的规律解决问题。渗透有序思考的方法,提高学生的概括、推理能力。
复习导入你还记得长方体正方体的表面积公式吗?长方体的表面积公式:
(长×宽+长×高+宽×高)×2
正方体是表面积公式:
( 棱长×棱长)×6情景导入1小华用10块棱长是1厘米的正方体摆出了一个立体图形(如图1)。如果再放上1块同样的正方体,并要求它至少有一个面和已有正方体的面完全接触,摆出的立体图形的表面积是多少平方厘米?理解题意:
解读图一的形状特点,计算出图一的表面积,再用棱长是1厘米的正方体摆一摆,看看多出几个面。我们可以先求出图1的露在外面表面积:
6×4+2×4=32(平方厘米)探究新知方法:
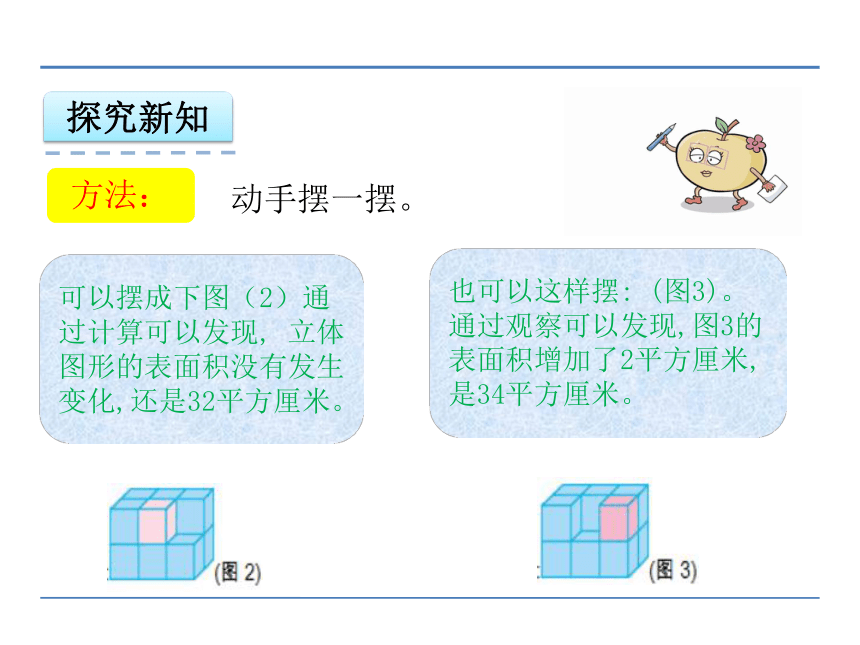
计算原立体图形的表面积。由于小正方体的棱长是1厘米,所以每个小正方体一个面的表面积是1平方厘米。可以摆成下图(2)通过计算可以发现, 立体图形的表面积没有发生变化,还是32平方厘米。探究新知方法:
动手摆一摆。也可以这样摆: (图3)。通过观察可以发现,图3的表面积增加了2平方厘米,是34平方厘米。可以摆成(图4)。通过观察可以发现,图4表面积增加了4平方厘米,是36平方厘米。探究新知方法:
动手摆一摆。也可以这样摆: (图5)。通过观察可以发现,图5的表面积增加了4平方厘米,是36平方厘米。图5探究新知解决问题:
解:图2:摆放的三个面接触,其表面积与原立体图形相同。
图3:摆放的有两个面接触,其表面积比原立体图形多2平方厘米。
图4和图5:摆放的有一个面接触,其表面积比原立体图形多4平方厘米。你发现了什么规律呢?摆放的正方体与原立体图形接触的面的多少影响摆放后立体图形的表面积。情景导入2从一张正方形纸上连续剪了5次,分别剪下它的 、 、、 和 。剪下纸片的总面积相当于原来正方形纸面积的几分之几?探究新知方法:
先通分。我们可以运用通分的方法解决问题。先把这组分数化成分母是32的分数,然后进行计算。探究新知方法:
发现规律。通过观察可以发现,这组分数是有规律的,即这几个分数的分子都是1,并且后一个分数的分母都是前一个分数分母的2倍。那么它们的和有什么规律呢?分析如下:可以发现:结果都比1小,正好小了1个分数单位。探究新知解决问题:
解:答:剪下纸片的总面积相当于原来正方形纸面积的三十二分之三十一。典题精讲解题思路:只要是分母是相临的两个数(如4和5) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。1.直接写得数。解答:典题精讲解题思路:观察图形仔细数一数有几个面接触。2.分别有几个面露再外面。解答:11 23( )( )易错提醒错误原因:没有正确理解正方体与长方体的性质。判断:正方体是长方体的的特殊情况,因此,正方体的性质也适应于长方体。 ( √ )错误解答课件PPT正确解答: (×)正方体有长方体的性质,而长方体没有正方体的性质。易错提醒正确解答解:学以致用1.把一个棱长为10厘米的正方体纸盒放在墙角处(如下图),有( )个面露在外面,露在外面的的面积是( )平方厘米 。3 300正方体有6个面,3个面靠墙,有3个面露在外面,请注意棱长为10厘米一个面就是100厘米,求出三个面。课件PPT2.用探究规律的方法计算。只要是分母是相临的两个数(如4和5) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。学以致用解:解:学以致用先数出有几个面露在外面,再根据棱长求面积。3.有若干个棱长为2dm的正方体纸箱放在墙角处,如下图所示,露在外面的面积是( )dm2。 52课件PPT4.用探究规律的方法计算。只要是分母是相临的两个数(如7和8) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。学以致用解:课件PPT5.下图是校运动会的领奖台示意图,它由4个棱长为4分米的正方体组成,有( )个面露在外面,露在外面的面积是( )分米 。先数出有21个面露在外面,再根据棱长4分米求一个面的面积再乘21。解:学以致用21 336课堂小结1. 新加的正方体与原立体图形的接触的面的多少影响摆放后立体图形的表面积,3个面接触,摆出的立体图形的表面积没有变化;2个面接触,摆出的立体图形的表面积比原立体图形多2平方厘米;1个面接触摆出的立体图形的表面积比原立体图形多4平方厘米。2.只要是分母是相临的两个数(如7和8) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。谢谢
复习导入你还记得长方体正方体的表面积公式吗?长方体的表面积公式:
(长×宽+长×高+宽×高)×2
正方体是表面积公式:
( 棱长×棱长)×6情景导入1小华用10块棱长是1厘米的正方体摆出了一个立体图形(如图1)。如果再放上1块同样的正方体,并要求它至少有一个面和已有正方体的面完全接触,摆出的立体图形的表面积是多少平方厘米?理解题意:
解读图一的形状特点,计算出图一的表面积,再用棱长是1厘米的正方体摆一摆,看看多出几个面。我们可以先求出图1的露在外面表面积:
6×4+2×4=32(平方厘米)探究新知方法:
计算原立体图形的表面积。由于小正方体的棱长是1厘米,所以每个小正方体一个面的表面积是1平方厘米。可以摆成下图(2)通过计算可以发现, 立体图形的表面积没有发生变化,还是32平方厘米。探究新知方法:
动手摆一摆。也可以这样摆: (图3)。通过观察可以发现,图3的表面积增加了2平方厘米,是34平方厘米。可以摆成(图4)。通过观察可以发现,图4表面积增加了4平方厘米,是36平方厘米。探究新知方法:
动手摆一摆。也可以这样摆: (图5)。通过观察可以发现,图5的表面积增加了4平方厘米,是36平方厘米。图5探究新知解决问题:
解:图2:摆放的三个面接触,其表面积与原立体图形相同。
图3:摆放的有两个面接触,其表面积比原立体图形多2平方厘米。
图4和图5:摆放的有一个面接触,其表面积比原立体图形多4平方厘米。你发现了什么规律呢?摆放的正方体与原立体图形接触的面的多少影响摆放后立体图形的表面积。情景导入2从一张正方形纸上连续剪了5次,分别剪下它的 、 、、 和 。剪下纸片的总面积相当于原来正方形纸面积的几分之几?探究新知方法:
先通分。我们可以运用通分的方法解决问题。先把这组分数化成分母是32的分数,然后进行计算。探究新知方法:
发现规律。通过观察可以发现,这组分数是有规律的,即这几个分数的分子都是1,并且后一个分数的分母都是前一个分数分母的2倍。那么它们的和有什么规律呢?分析如下:可以发现:结果都比1小,正好小了1个分数单位。探究新知解决问题:
解:答:剪下纸片的总面积相当于原来正方形纸面积的三十二分之三十一。典题精讲解题思路:只要是分母是相临的两个数(如4和5) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。1.直接写得数。解答:典题精讲解题思路:观察图形仔细数一数有几个面接触。2.分别有几个面露再外面。解答:11 23( )( )易错提醒错误原因:没有正确理解正方体与长方体的性质。判断:正方体是长方体的的特殊情况,因此,正方体的性质也适应于长方体。 ( √ )错误解答课件PPT正确解答: (×)正方体有长方体的性质,而长方体没有正方体的性质。易错提醒正确解答解:学以致用1.把一个棱长为10厘米的正方体纸盒放在墙角处(如下图),有( )个面露在外面,露在外面的的面积是( )平方厘米 。3 300正方体有6个面,3个面靠墙,有3个面露在外面,请注意棱长为10厘米一个面就是100厘米,求出三个面。课件PPT2.用探究规律的方法计算。只要是分母是相临的两个数(如4和5) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。学以致用解:解:学以致用先数出有几个面露在外面,再根据棱长求面积。3.有若干个棱长为2dm的正方体纸箱放在墙角处,如下图所示,露在外面的面积是( )dm2。 52课件PPT4.用探究规律的方法计算。只要是分母是相临的两个数(如7和8) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。学以致用解:课件PPT5.下图是校运动会的领奖台示意图,它由4个棱长为4分米的正方体组成,有( )个面露在外面,露在外面的面积是( )分米 。先数出有21个面露在外面,再根据棱长4分米求一个面的面积再乘21。解:学以致用21 336课堂小结1. 新加的正方体与原立体图形的接触的面的多少影响摆放后立体图形的表面积,3个面接触,摆出的立体图形的表面积没有变化;2个面接触,摆出的立体图形的表面积比原立体图形多2平方厘米;1个面接触摆出的立体图形的表面积比原立体图形多4平方厘米。2.只要是分母是相临的两个数(如7和8) 分子为1 它们的差分母是两数的积,分子不变。它们的和是分子是两数的和,分子是两数的积。谢谢
