人教高中数学必修2 空间几何体复习小结(1)
文档属性
| 名称 | 人教高中数学必修2 空间几何体复习小结(1) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-11 00:00:00 | ||
图片预览

文档简介
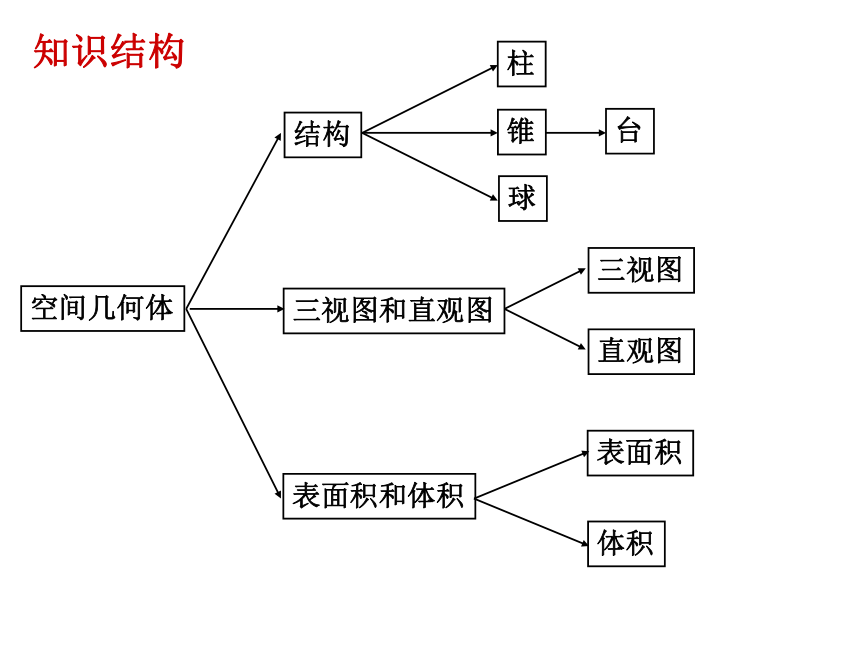
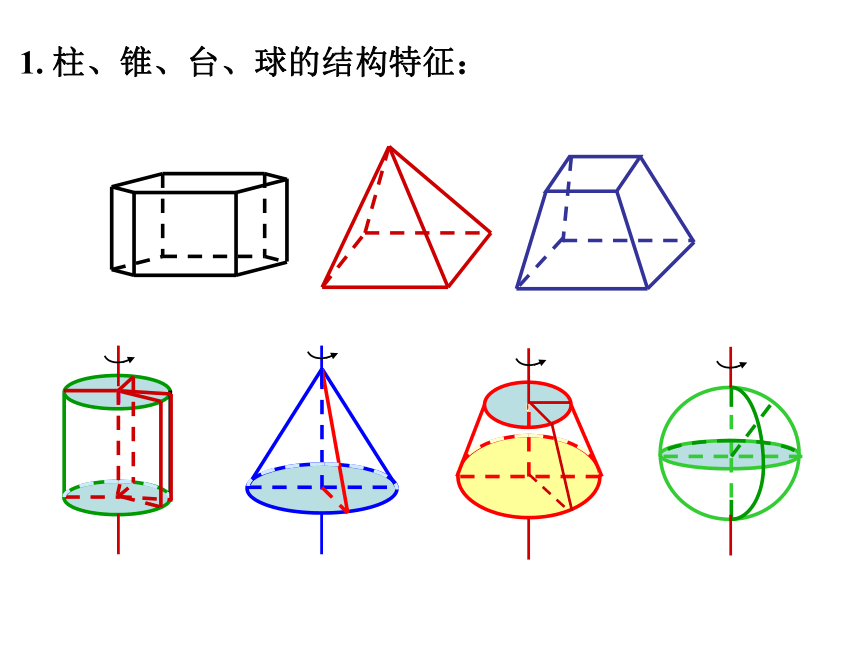
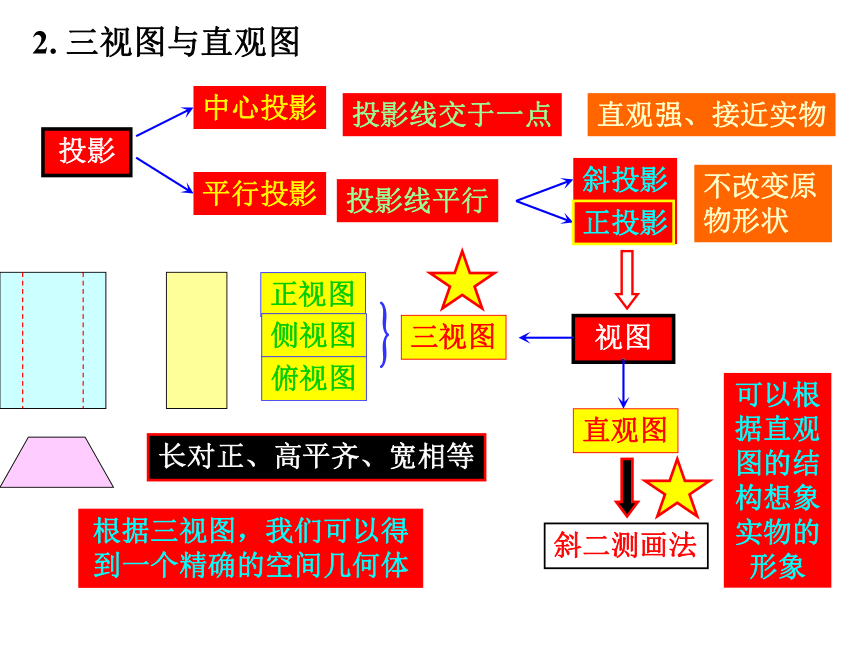
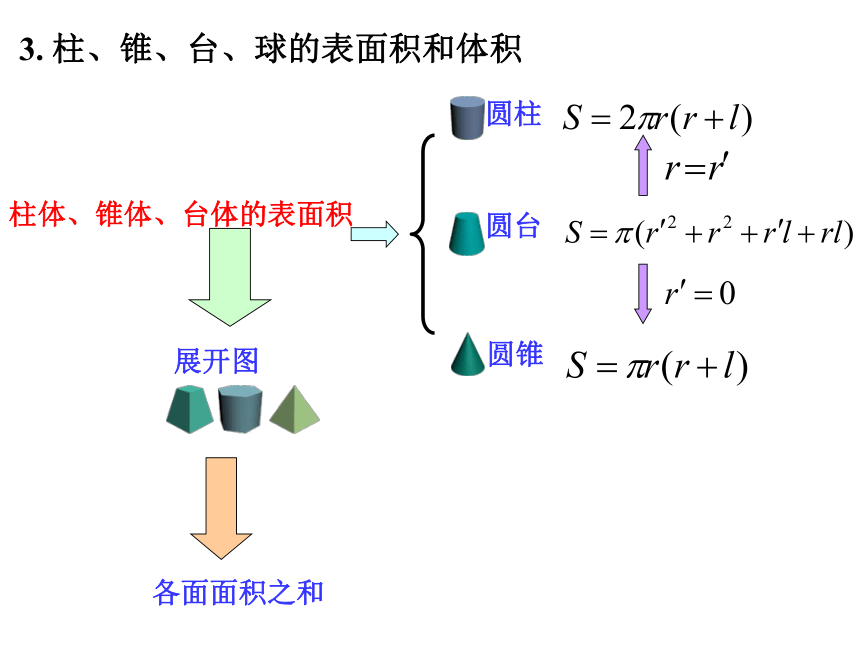
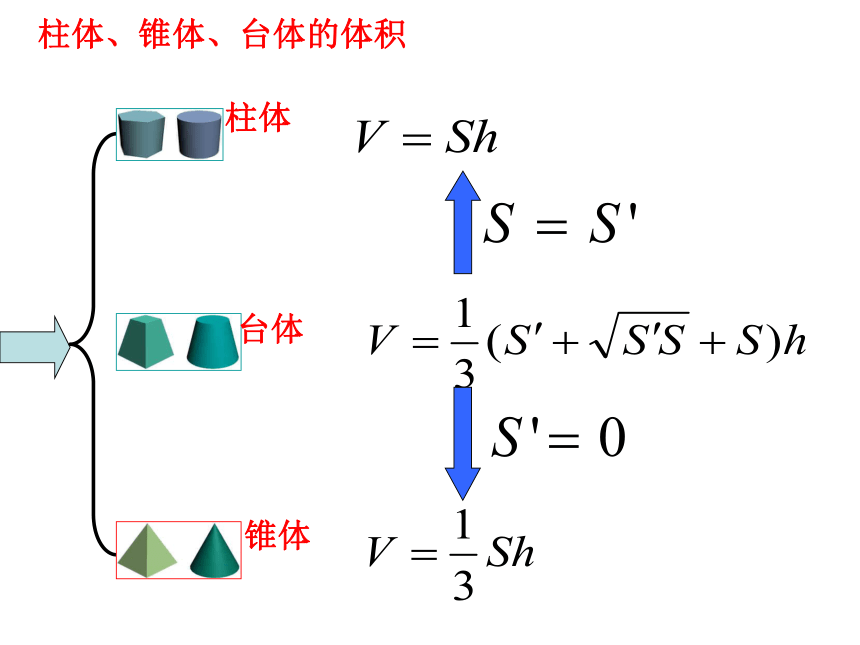
课件13张PPT。第一章 复习小结空间几何体结构三视图和直观图表面积和体积柱锥球台三视图直观图表面积体积知识结构1. 柱、锥、台、球的结构特征: 投影视图根据三视图,我们可以得到一个精确的空间几何体可以根据直观图的结构想象实物的形象2. 三视图与直观图柱体、锥体、台体的表面积3. 柱、锥、台、球的表面积和体积柱体、锥体、台体的体积定理: 半径是R的球的体积定理: 半径是R的球的表面积球的体积、表面积的计算公式例1.一个红色的棱长为4cm的立方体,将其适当分割成棱长为1cm的小正方形,问:
(1)共得到多少个棱长为1cm的小正方体?
(2)三面涂色的小正方体有多少个?表面积之和为多少?
(3)二面涂色的小正方体有多少个?表面积之和为多少?
(4)一面涂色的小正方体有多少个?表面积之和为多少?
(5)六个面均没有涂色的小正方体有多少个?表面积之和为多少?它们占有多少立方厘米的空间?解:每层16个小正方体,共4层,故共得到64个棱长为1cm的小正方体;(2)三面涂色的小正方体位于立方体
的八个顶点处,故有8个,表面积之和为解:每层16个小正方体,共4层,故共得到64个棱长为1cm的小正方体;(2)三面涂色的小正方体位于立方体
的八个顶点处,故有8个,表面积之和为(3)二面涂色的小正方体位于立方体每条棱上对应有2个,的两个面的公共棱且非顶点处,共个,表面积之和为(4)一面涂色的小正方体位于立方体的面内,每个面对应有4个,共个,表面积之和为(5)六个面均没有涂色的小正方体有个,表面积之和为它们的体积之和为例2.已知,棱长都相等的正三棱锥内接于一个球,
某学生画出四个过球心的平面截球和正三棱锥所得
的图形,如下图所示,则( ).CC课后作业1. 复习参考题A组5、6、7 B组2题3. 预习2.1.12. 《新概念》章末复习
(1)共得到多少个棱长为1cm的小正方体?
(2)三面涂色的小正方体有多少个?表面积之和为多少?
(3)二面涂色的小正方体有多少个?表面积之和为多少?
(4)一面涂色的小正方体有多少个?表面积之和为多少?
(5)六个面均没有涂色的小正方体有多少个?表面积之和为多少?它们占有多少立方厘米的空间?解:每层16个小正方体,共4层,故共得到64个棱长为1cm的小正方体;(2)三面涂色的小正方体位于立方体
的八个顶点处,故有8个,表面积之和为解:每层16个小正方体,共4层,故共得到64个棱长为1cm的小正方体;(2)三面涂色的小正方体位于立方体
的八个顶点处,故有8个,表面积之和为(3)二面涂色的小正方体位于立方体每条棱上对应有2个,的两个面的公共棱且非顶点处,共个,表面积之和为(4)一面涂色的小正方体位于立方体的面内,每个面对应有4个,共个,表面积之和为(5)六个面均没有涂色的小正方体有个,表面积之和为它们的体积之和为例2.已知,棱长都相等的正三棱锥内接于一个球,
某学生画出四个过球心的平面截球和正三棱锥所得
的图形,如下图所示,则( ).CC课后作业1. 复习参考题A组5、6、7 B组2题3. 预习2.1.12. 《新概念》章末复习
