人教高中数学必修2 第一章空间几何体的小结复习
文档属性
| 名称 | 人教高中数学必修2 第一章空间几何体的小结复习 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-11 00:00:00 | ||
图片预览



文档简介
课件29张PPT。空间几何体的结构、三视图、直观图
复习小结立体几何复习建议1、掌握三基
(1)基本知识
(2)基本技能:识图、作图
(3)基本思想和方法:转化与化归、运动变化
2、充分利用模型
3、熟记一些重要结论
4、树立自信心立体几何复习要领
立体几何点线面,做图识图是关键;
理解概念和定理,图形处理割补添;
学会分析找思路,一作二证三计算;
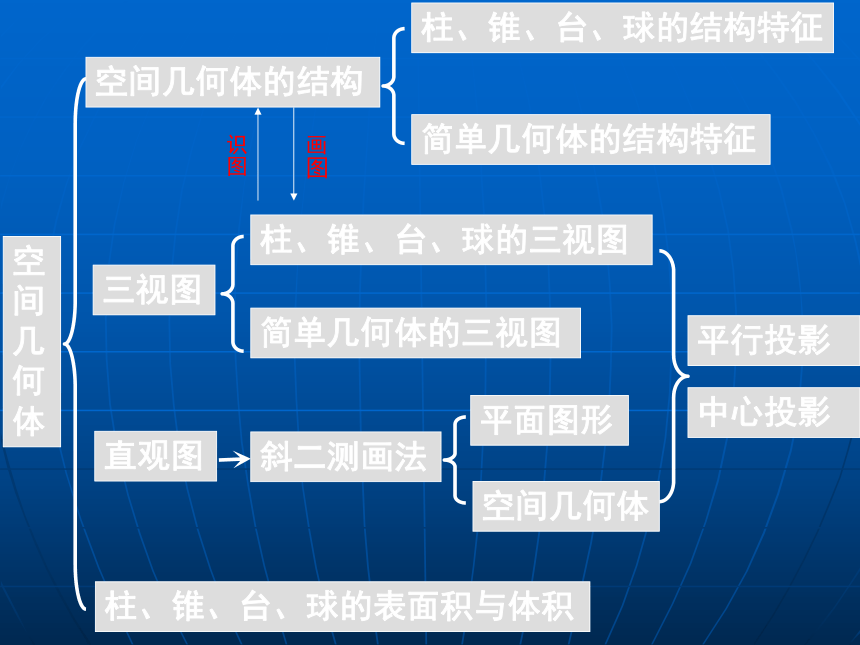
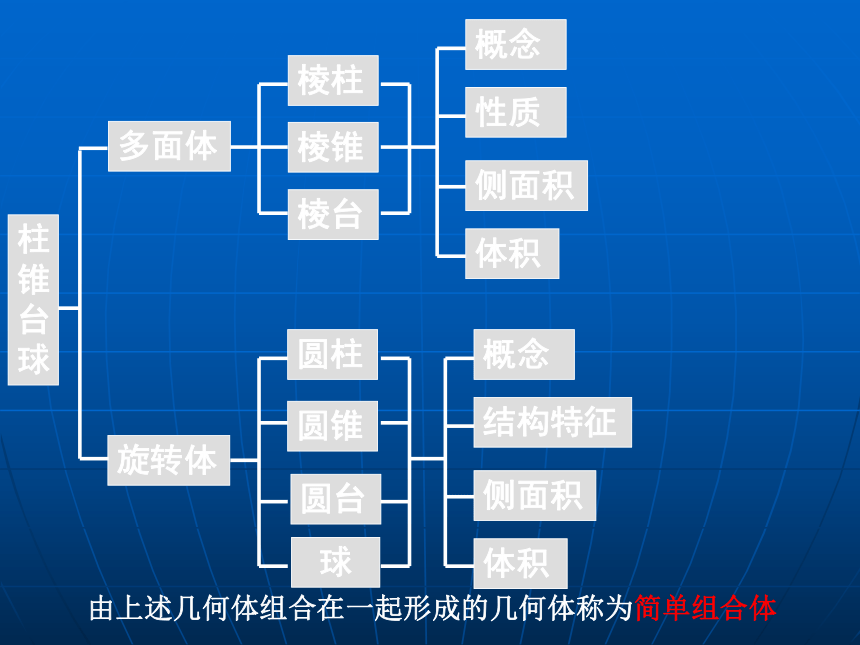
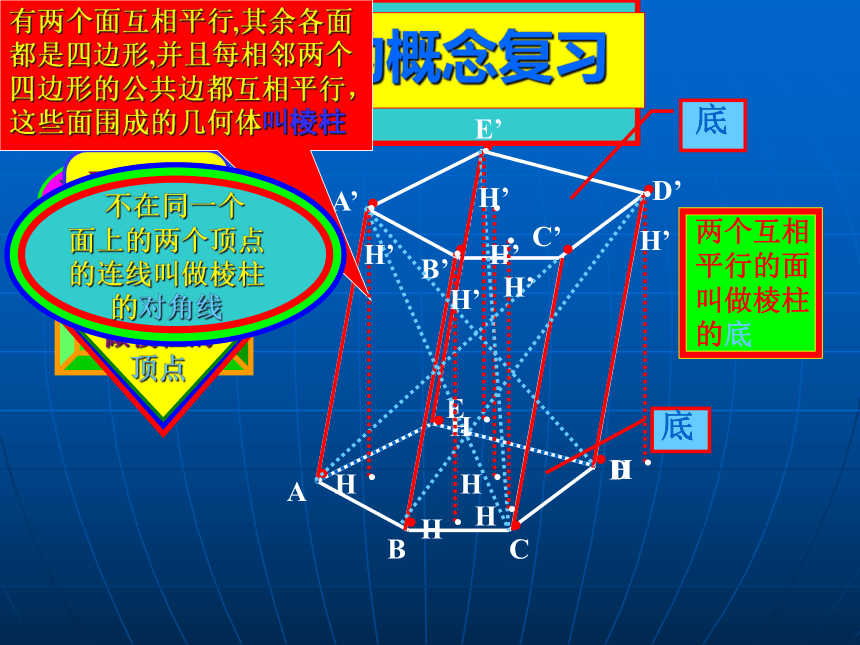
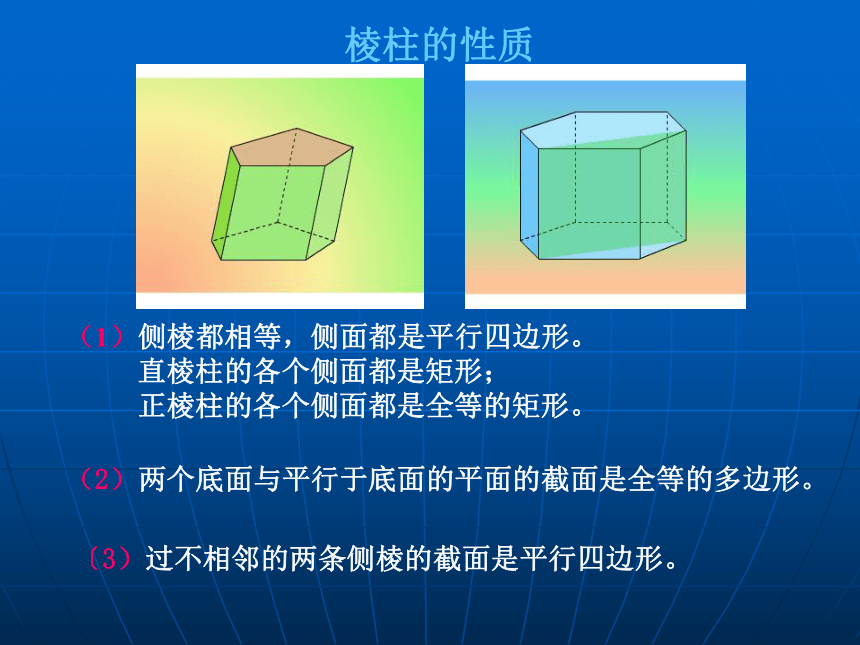
善于思考和勤问,回归课本要牢记;空间几何体空间几何体的结构柱、锥、台、球的结构特征简单几何体的结构特征三视图柱、锥、台、球的三视图简单几何体的三视图直观图斜二测画法平面图形空间几何体中心投影柱、锥、台、球的表面积与体积平行投影画图识图柱锥台球圆锥圆台多面体旋转体圆柱棱柱棱锥棱台概念结构特征侧面积体积 球概念性质侧面积体积由上述几何体组合在一起形成的几何体称为简单组合体棱柱的性质(2)两个底面与平行于底面的平面的截面是全等的多边形。 〔3)过不相邻的两条侧棱的截面是平行四边形。 (1)侧棱都相等,侧面都是平行四边形。
直棱柱的各个侧面都是矩形;
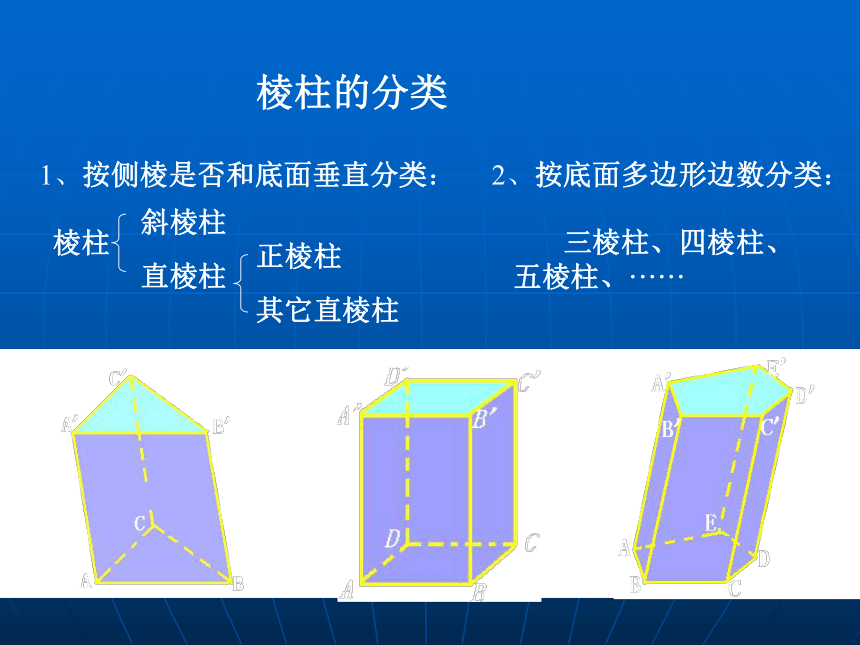
正棱柱的各个侧面都是全等的矩形。1、按侧棱是否和底面垂直分类:棱柱斜棱柱直棱柱正棱柱其它直棱柱2、按底面多边形边数分类:棱柱的分类 三棱柱、四棱柱、
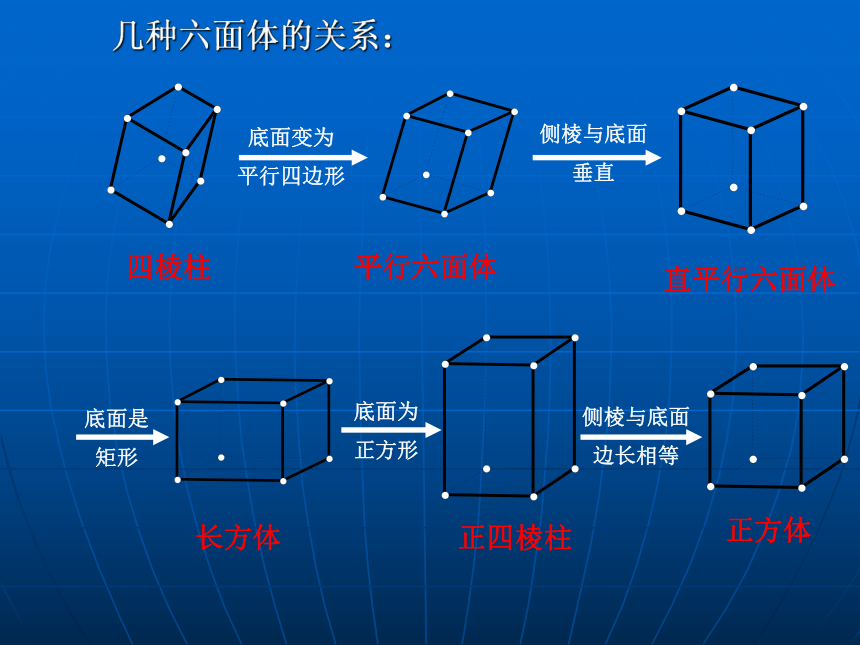
五棱柱、······四棱柱平行六面体长方体直平行六面体正四棱柱正方体底面变为
平行四边形侧棱与底面
垂直底面是
矩形底面为
正方形侧棱与底面
边长相等几种六面体的关系:【知识梳理】棱锥 1、定义:
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥。
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥。2、性质
Ⅰ、正棱锥的性质
(1)各侧棱相等,各侧面都是全等的等腰三角形。
(2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。正棱锥性质2棱锥的高、斜高和斜高在底面的射影组成一个直角三角形。棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形PARt⊿ PEORt⊿ POBRt⊿ PEBRt⊿ BEO棱台由棱锥截得而成,所以在棱台中也有类似的直角梯形。棱锥棱锥正四棱锥正三棱锥正四面体体积V=Sh/3顶点在底面正多边形的射影是底面的中心棱柱侧棱垂直于底面直棱柱底面是正多边形正棱柱棱锥底面为正多边形,顶点在底面的射影为正多边形的中心正棱锥正棱台 由正棱锥截的的棱台 处理台体的思想方法是还台于锥。有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱。一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台(1)侧棱都相等:
(2)侧面都是平行四边形:
(3)两个底面与平行底面的截面是全等的多边形;平行底面的截面与底面相似。(1)上下两个底面互相平行;
(2)侧棱的延长线相交于一点;侧面展开图是一组平行四边形。侧面展开图是一组三角形。侧面展开图是一组梯形;V=Sh旋转体圆柱 圆锥 圆台 球 分别以矩形、直角三角形的直角边、
直角梯形垂直于底边的腰所在的直线为旋
转轴,其余各边旋转而成的曲面所围成的
几何体, 分别叫做圆柱,圆锥,圆台。圆柱圆锥圆台 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。圆锥的结构特征球的结构特征 以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作球面,球面所围成的几何体叫作球体,简称球。球心半径直径O球的基本属性:
球面可看作与定点(球心)的距离
等于定长(半径)的所有点的集合.中心投影法投射线投射中心投影面投影物体位置改变,投影大小也改变 把光由一点向外散射形成的投影,叫做中心投影。平行投影法ABCDABCD投射线与投影面相倾斜的平行投影法
-----斜投影法
投射线与投影面相互垂直的平行投影法
--------正投影法在一束平行光线的照射下形成的投射,叫做平行投影。
平行投影分正投影和斜投影两种。 三视图的形成物体向投影面投影所得到的图形称为视图。如果物体向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图。三视图
正(主)视图——从正面看到的图
侧(左)视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等.圆柱,圆锥三视图正视图侧视图俯视图正视图侧视图俯视图球的三视图正视图侧视图俯视图几种基本几何体三视图 1.圆柱、圆锥、球的三视图 ·几种基本几何体的三视图
2.棱柱、棱锥的三视图画直观图的方法叫做斜二测画法。原图直观图原图直观图1)画水平放置的平面多边形的直观图关键是确定多边形的顶点位置。确定点的位置,可以借助于平面直角坐标系。
2)平面图形用其直观图表示时,一般说来,平行关系不变;点的共线性不变;线的共点性不变;但角的大小有变化;(特别是垂直关系发生变化)有些线段的度量关系也发生变化。因此,图形的形状发生变化,这种变化,目的是为了图形富有立体感。(1)在已知图形中取互相垂直的x轴和y轴,两轴相交于o点.画直观图时,
把它画成对应的x′轴、y′轴,使
它确定的平面表示水平平面。
(2)原图形中平行于x或y轴的线段,在直观图中分别画成平行于x′或y′轴的线段.
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度为原来的一半.斜二测画法的步骤:
复习小结立体几何复习建议1、掌握三基
(1)基本知识
(2)基本技能:识图、作图
(3)基本思想和方法:转化与化归、运动变化
2、充分利用模型
3、熟记一些重要结论
4、树立自信心立体几何复习要领
立体几何点线面,做图识图是关键;
理解概念和定理,图形处理割补添;
学会分析找思路,一作二证三计算;
善于思考和勤问,回归课本要牢记;空间几何体空间几何体的结构柱、锥、台、球的结构特征简单几何体的结构特征三视图柱、锥、台、球的三视图简单几何体的三视图直观图斜二测画法平面图形空间几何体中心投影柱、锥、台、球的表面积与体积平行投影画图识图柱锥台球圆锥圆台多面体旋转体圆柱棱柱棱锥棱台概念结构特征侧面积体积 球概念性质侧面积体积由上述几何体组合在一起形成的几何体称为简单组合体棱柱的性质(2)两个底面与平行于底面的平面的截面是全等的多边形。 〔3)过不相邻的两条侧棱的截面是平行四边形。 (1)侧棱都相等,侧面都是平行四边形。
直棱柱的各个侧面都是矩形;
正棱柱的各个侧面都是全等的矩形。1、按侧棱是否和底面垂直分类:棱柱斜棱柱直棱柱正棱柱其它直棱柱2、按底面多边形边数分类:棱柱的分类 三棱柱、四棱柱、
五棱柱、······四棱柱平行六面体长方体直平行六面体正四棱柱正方体底面变为
平行四边形侧棱与底面
垂直底面是
矩形底面为
正方形侧棱与底面
边长相等几种六面体的关系:【知识梳理】棱锥 1、定义:
有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫棱锥。
如果一个棱锥的底面是正多边形,并且顶点在底面的射影是底面中心,这样的棱锥叫做正棱锥。2、性质
Ⅰ、正棱锥的性质
(1)各侧棱相等,各侧面都是全等的等腰三角形。
(2)棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形;棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。正棱锥性质2棱锥的高、斜高和斜高在底面的射影组成一个直角三角形。棱锥的高、侧棱和侧棱在底面的射影组成一个直角三角形PARt⊿ PEORt⊿ POBRt⊿ PEBRt⊿ BEO棱台由棱锥截得而成,所以在棱台中也有类似的直角梯形。棱锥棱锥正四棱锥正三棱锥正四面体体积V=Sh/3顶点在底面正多边形的射影是底面的中心棱柱侧棱垂直于底面直棱柱底面是正多边形正棱柱棱锥底面为正多边形,顶点在底面的射影为正多边形的中心正棱锥正棱台 由正棱锥截的的棱台 处理台体的思想方法是还台于锥。有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,这些面围成的几何体叫做棱柱。一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分叫作棱台(1)侧棱都相等:
(2)侧面都是平行四边形:
(3)两个底面与平行底面的截面是全等的多边形;平行底面的截面与底面相似。(1)上下两个底面互相平行;
(2)侧棱的延长线相交于一点;侧面展开图是一组平行四边形。侧面展开图是一组三角形。侧面展开图是一组梯形;V=Sh旋转体圆柱 圆锥 圆台 球 分别以矩形、直角三角形的直角边、
直角梯形垂直于底边的腰所在的直线为旋
转轴,其余各边旋转而成的曲面所围成的
几何体, 分别叫做圆柱,圆锥,圆台。圆柱圆锥圆台 以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的曲面所围成的几何体叫做圆锥。圆锥的结构特征球的结构特征 以半圆的直径所在的直线为旋转轴,将半圆旋转所形成的曲面叫作球面,球面所围成的几何体叫作球体,简称球。球心半径直径O球的基本属性:
球面可看作与定点(球心)的距离
等于定长(半径)的所有点的集合.中心投影法投射线投射中心投影面投影物体位置改变,投影大小也改变 把光由一点向外散射形成的投影,叫做中心投影。平行投影法ABCDABCD投射线与投影面相倾斜的平行投影法
-----斜投影法
投射线与投影面相互垂直的平行投影法
--------正投影法在一束平行光线的照射下形成的投射,叫做平行投影。
平行投影分正投影和斜投影两种。 三视图的形成物体向投影面投影所得到的图形称为视图。如果物体向三个互相垂直的投影面分别投影,所得到的三个图形摊平在一个平面上,则就是三视图。三视图
正(主)视图——从正面看到的图
侧(左)视图——从左面看到的图
俯视图——从上面看到的图
画物体的三视图时,要符合如下原则:
位置:正视图 侧视图
俯视图
大小:长对正,高平齐,宽相等.圆柱,圆锥三视图正视图侧视图俯视图正视图侧视图俯视图球的三视图正视图侧视图俯视图几种基本几何体三视图 1.圆柱、圆锥、球的三视图 ·几种基本几何体的三视图
2.棱柱、棱锥的三视图画直观图的方法叫做斜二测画法。原图直观图原图直观图1)画水平放置的平面多边形的直观图关键是确定多边形的顶点位置。确定点的位置,可以借助于平面直角坐标系。
2)平面图形用其直观图表示时,一般说来,平行关系不变;点的共线性不变;线的共点性不变;但角的大小有变化;(特别是垂直关系发生变化)有些线段的度量关系也发生变化。因此,图形的形状发生变化,这种变化,目的是为了图形富有立体感。(1)在已知图形中取互相垂直的x轴和y轴,两轴相交于o点.画直观图时,
把它画成对应的x′轴、y′轴,使
它确定的平面表示水平平面。
(2)原图形中平行于x或y轴的线段,在直观图中分别画成平行于x′或y′轴的线段.
(3)已知图形中平行于x轴的线段,在直观图中保持原长度不变;平行于y轴的线段,长度为原来的一半.斜二测画法的步骤:
