11.1.2 三角形的高、中线与角平分线(课件+swf素材)
文档属性
| 名称 | 11.1.2 三角形的高、中线与角平分线(课件+swf素材) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-11 16:42:49 | ||
图片预览




文档简介
课件29张PPT。11.1 与三角形有关的线段第2课时 三角形的高、中
线与角平分线第十一章 三角形1课堂讲解三角形的高
三角形的中线
三角形的角平分线2课时流程逐点
导讲练课堂小结作业提升回顾旧知垂线的定义:线段中点的定义: 当两条直线相交所成的四个角巾,有一个角是直角时,就说这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线. 把一条线段分成两条相等的线段的点.角平分线的定义: 一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.知1-导1知识点三角形的高 你能过三角形的一个顶点,你能画出它的
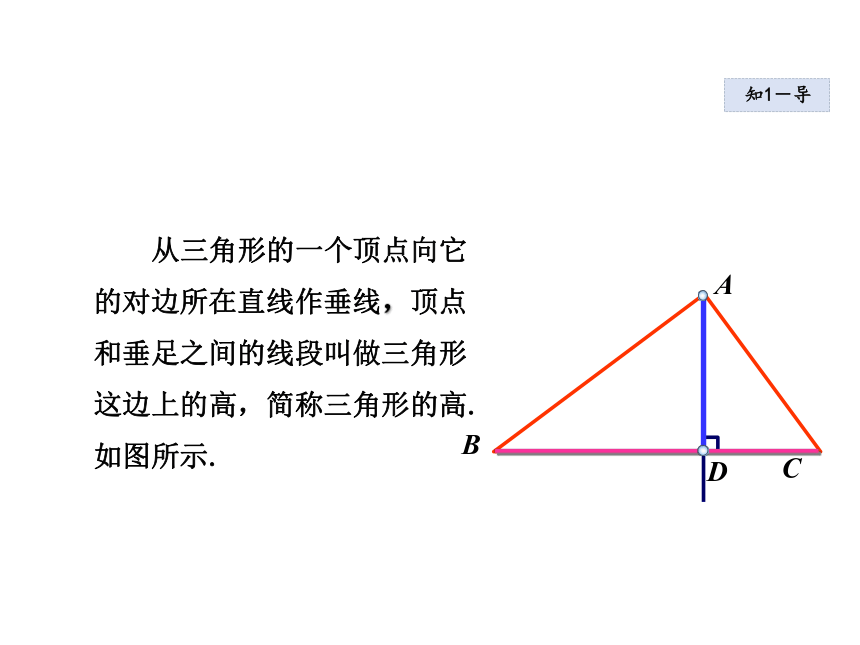
对边的垂线吗?你还记得 “过一点画已知直线的垂线” 吗? 从三角形的一个顶点向它
的对边所在直线作垂线,顶点
和垂足之间的线段叫做三角形
这边上的高,简称三角形的高.
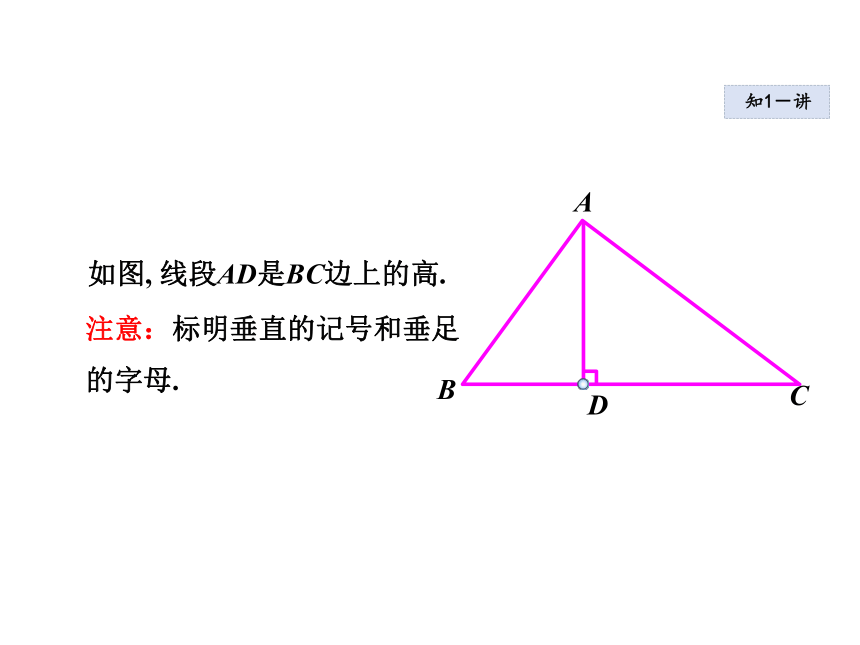
如图所示.ABC知1-导如图, 线段AD是BC边上的高.注意:标明垂直的记号和垂足
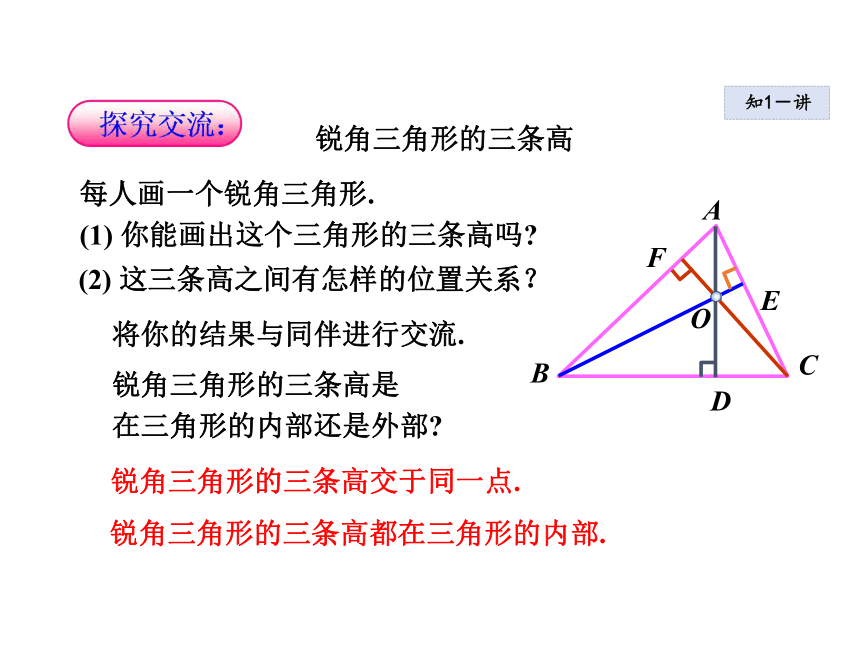
的字母.知1-讲锐角三角形的三条高每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.锐角三角形的三条高是
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部.知1-讲知1-讲直角三角形的三条高在纸上画出一个直角三角形.将你的结果与同伴进行交流.ABC(1)画出直角三角形的三条高.直角边BC边上的高是______; AB直角边AB边上的高是______;CB(2)它们有怎样的位置关系?D斜边AC边上的高是_______. BD●直角三角形的三条高交于直角顶点.ABCDEF钝角三角形的三条高(1) 钝角三角形的三条高交于
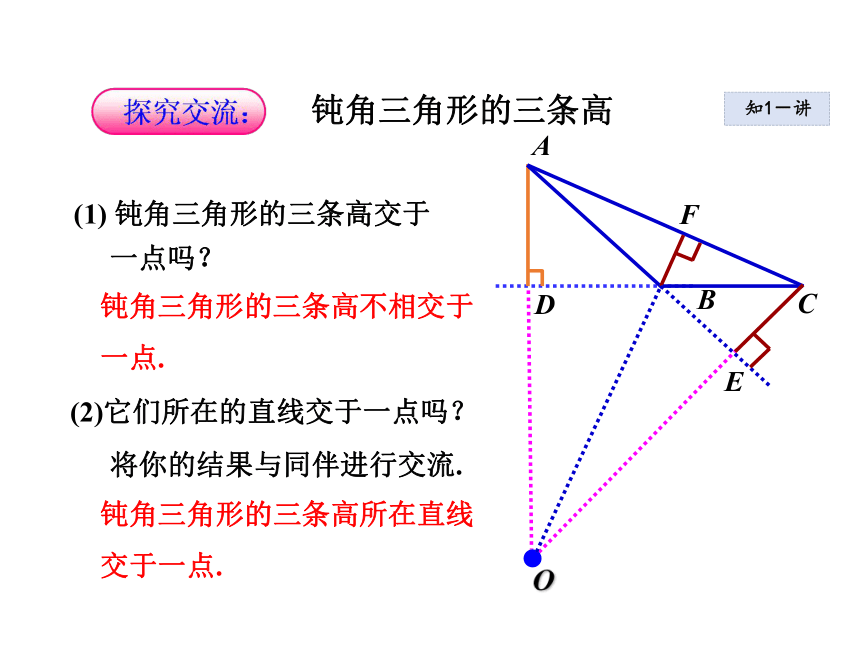
一点吗?(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.O钝角三角形的三条高不相交于
一点.钝角三角形的三条高所在直线
交于一点.知1-讲 叫做三角形这边上的高.从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段知1-讲三角形的三条高的特性:高所在的直线是否相交高之间是否相交高在三角形内部的数量钝角三角形直角三角形锐角三角形311相交相交不相交相交相交相交三条高所在直线的交点的位置三角形内部直角顶点三角形外部知1-讲如图,(1) (2)和(3)中的三个∠B有什么不同?这三条△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?知1-练1(1)中的∠B是锐角,高AD在△ABC内部.
(2)中的∠B是直角,高AD与边AB重合.
(3)中的∠B是钝角,高AD的垂足在CB的延长线上,
即高AD在△ABC的外部.
当∠C是锐角时,如果∠B是锐角,高AD在△ABC
的内部;如果∠B是直角,高AD与边AB重合;如
果∠B是钝角,高AD的垂足在CB的延长线上,即
高AD在△ABC的外部.解:知1-练规律:知1-练在直角三角形中,有两条高是它的________,
另一条高在这个三角形的________.锐角三角形
的三条高的交点在______________,直角三角形的三条高的交点在_______________________,钝角三角形的三条高所在直线的交点在_________________.2直角边内部三角形的内部三角形的外部两直角边的交点处知2-导2知识点三角形的中线如图 (1),连接△ABC的顶点A和 它所对的边BC的中点D,
所得线段AD叫做 △ABC的边BC上的中线.用同样方法, 你能画出△ABC 的另两条边上的中 线吗?知2-导在三角形中,连接一个顶点与它对边中点的线段,
叫做这个三角形这边上的中线.如图 (2),三角形的三条中线相交于一点.三角形三
条中线的交点叫做三角形的重心.取一块质地均匀的 三角形木板,顶住三条 中线的
交点,木板会保 持平衡,这个平衡点就 是这块三
角形木板的 重心.知2-讲在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12 cm和15 cm两部分,求△ABC的各边长.
知2-讲例1因为中线BD将△ABC的周长分成两部分:(BC+
CD)和(AD+AB),无法确定谁为12 cm,谁为15
cm,故应分类讨论;另外题中涉及线段较多,因
此可建立方程的模型,利用设未知数来求解.导引:设AB=x cm,则AD=CD= x cm.
(1)如图①,若AB+AD=12 cm,则x+ x=12.解得x=8,
即AB=AC=8 cm,则CD=4 cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8 cm,8 cm,11 cm.
(2)如图②,若AB+AD=15 cm,则x+ x=15.
解得x=10,即AB=AC=10 cm,则CD=5 cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10 cm,10 cm,7 cm.
综上所述,△ABC的三边长分别为8 cm,8 cm,11 cm或10 cm,
10 cm,7 cm.解:知2-讲知2-练填空: 如图(1),AD,BE,CF是△ABC的三条中线,则AB= 2 __________, BD=_______, AE=
________.1AD或BFCDAC知2-练三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形2B知2-练如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定3A知3-导3知识点三角形的角平分线 如果现在你手上有一张画着一个三角形的薄纸,
你能想几种办法画出它的一个内角的平分线?叫做三角形的角平分线.ABCD因为AD是△ABC的角平分线,任意画一个三角形,然后利用
量角器画出这个三角形三个角
的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的
内部.知3-讲知3-讲ACBFEDO因为BE是△ABC的角平分线,所以______=________= _______.所以∠ACB=2_______
=2__________.∠ABE∠CBE∠ABC∠ACF因为CF是△ABC的角平分线,∠BCF知3-讲1.三角形的角平分线与角的平分线的区别是:
三角形的角平分线是线段,而角的平分线是一条射线;
它们的联系是都是平分角。2.三角形的角平分线判别的“两种方法”
(1)看该线段是否分三角形的内角为相等的两部分.
(2)看线段的两个端点,其中一个端点是三角形的顶
点,另一个端点要落在对边上.如下页图(2),AD, BE, CF是△ ABC的三条角平分线,则∠1=______, ∠3=
_______, ∠ACB= 2_______.
1知3-练∠2∠ABC∠4今天我们学了什么呢?
1.三角形的高、中线、角平分线等有关概念及它们
的画法.
2.三角形的高、中线、角平分线几何表达及简单应
用.完成教材P8T3、T4、P9T8、T9
线与角平分线第十一章 三角形1课堂讲解三角形的高
三角形的中线
三角形的角平分线2课时流程逐点
导讲练课堂小结作业提升回顾旧知垂线的定义:线段中点的定义: 当两条直线相交所成的四个角巾,有一个角是直角时,就说这两条直线互相垂直, 其中一条直线叫做另一条直线的垂线. 把一条线段分成两条相等的线段的点.角平分线的定义: 一条射线把一个角分成两个相等的角,这条射线叫做这个角的平分线.知1-导1知识点三角形的高 你能过三角形的一个顶点,你能画出它的
对边的垂线吗?你还记得 “过一点画已知直线的垂线” 吗? 从三角形的一个顶点向它
的对边所在直线作垂线,顶点
和垂足之间的线段叫做三角形
这边上的高,简称三角形的高.
如图所示.ABC知1-导如图, 线段AD是BC边上的高.注意:标明垂直的记号和垂足
的字母.知1-讲锐角三角形的三条高每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗?(2) 这三条高之间有怎样的位置关系?将你的结果与同伴进行交流.锐角三角形的三条高是
在三角形的内部还是外部?ABCDEF锐角三角形的三条高交于同一点.锐角三角形的三条高都在三角形的内部.知1-讲知1-讲直角三角形的三条高在纸上画出一个直角三角形.将你的结果与同伴进行交流.ABC(1)画出直角三角形的三条高.直角边BC边上的高是______; AB直角边AB边上的高是______;CB(2)它们有怎样的位置关系?D斜边AC边上的高是_______. BD●直角三角形的三条高交于直角顶点.ABCDEF钝角三角形的三条高(1) 钝角三角形的三条高交于
一点吗?(2)它们所在的直线交于一点吗?将你的结果与同伴进行交流.O钝角三角形的三条高不相交于
一点.钝角三角形的三条高所在直线
交于一点.知1-讲 叫做三角形这边上的高.从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段知1-讲三角形的三条高的特性:高所在的直线是否相交高之间是否相交高在三角形内部的数量钝角三角形直角三角形锐角三角形311相交相交不相交相交相交相交三条高所在直线的交点的位置三角形内部直角顶点三角形外部知1-讲如图,(1) (2)和(3)中的三个∠B有什么不同?这三条△ABC的边BC上的高AD在各自三角形的什么位置?你能说出其中的规律吗?知1-练1(1)中的∠B是锐角,高AD在△ABC内部.
(2)中的∠B是直角,高AD与边AB重合.
(3)中的∠B是钝角,高AD的垂足在CB的延长线上,
即高AD在△ABC的外部.
当∠C是锐角时,如果∠B是锐角,高AD在△ABC
的内部;如果∠B是直角,高AD与边AB重合;如
果∠B是钝角,高AD的垂足在CB的延长线上,即
高AD在△ABC的外部.解:知1-练规律:知1-练在直角三角形中,有两条高是它的________,
另一条高在这个三角形的________.锐角三角形
的三条高的交点在______________,直角三角形的三条高的交点在_______________________,钝角三角形的三条高所在直线的交点在_________________.2直角边内部三角形的内部三角形的外部两直角边的交点处知2-导2知识点三角形的中线如图 (1),连接△ABC的顶点A和 它所对的边BC的中点D,
所得线段AD叫做 △ABC的边BC上的中线.用同样方法, 你能画出△ABC 的另两条边上的中 线吗?知2-导在三角形中,连接一个顶点与它对边中点的线段,
叫做这个三角形这边上的中线.如图 (2),三角形的三条中线相交于一点.三角形三
条中线的交点叫做三角形的重心.取一块质地均匀的 三角形木板,顶住三条 中线的
交点,木板会保 持平衡,这个平衡点就 是这块三
角形木板的 重心.知2-讲在△ABC中,AB=AC,AC边上的中线BD把△ABC的周长分为12 cm和15 cm两部分,求△ABC的各边长.
知2-讲例1因为中线BD将△ABC的周长分成两部分:(BC+
CD)和(AD+AB),无法确定谁为12 cm,谁为15
cm,故应分类讨论;另外题中涉及线段较多,因
此可建立方程的模型,利用设未知数来求解.导引:设AB=x cm,则AD=CD= x cm.
(1)如图①,若AB+AD=12 cm,则x+ x=12.解得x=8,
即AB=AC=8 cm,则CD=4 cm.故BC=15-4=11(cm).
此时AB+AC>BC,三角形存在,
所以三边长分别为8 cm,8 cm,11 cm.
(2)如图②,若AB+AD=15 cm,则x+ x=15.
解得x=10,即AB=AC=10 cm,则CD=5 cm.
故BC=12-5=7(cm).
显然此时三角形存在,所以三边长分别为10 cm,10 cm,7 cm.
综上所述,△ABC的三边长分别为8 cm,8 cm,11 cm或10 cm,
10 cm,7 cm.解:知2-讲知2-练填空: 如图(1),AD,BE,CF是△ABC的三条中线,则AB= 2 __________, BD=_______, AE=
________.1AD或BFCDAC知2-练三角形一边上的中线把原三角形一定分成两个( )
A.形状相同的三角形 B.面积相等的三角形
C.直角三角形 D.周长相等的三角形2B知2-练如图,已知BD是△ABC的中线,AB=5,BC=3,△ABD和△BCD的周长的差是( )
A.2 B.3 C.6 D.不能确定3A知3-导3知识点三角形的角平分线 如果现在你手上有一张画着一个三角形的薄纸,
你能想几种办法画出它的一个内角的平分线?叫做三角形的角平分线.ABCD因为AD是△ABC的角平分线,任意画一个三角形,然后利用
量角器画出这个三角形三个角
的角平分线,你发现了什么?●●在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,三角形的三条角平分线相交于一点,交点在三角形的
内部.知3-讲知3-讲ACBFEDO因为BE是△ABC的角平分线,所以______=________= _______.所以∠ACB=2_______
=2__________.∠ABE∠CBE∠ABC∠ACF因为CF是△ABC的角平分线,∠BCF知3-讲1.三角形的角平分线与角的平分线的区别是:
三角形的角平分线是线段,而角的平分线是一条射线;
它们的联系是都是平分角。2.三角形的角平分线判别的“两种方法”
(1)看该线段是否分三角形的内角为相等的两部分.
(2)看线段的两个端点,其中一个端点是三角形的顶
点,另一个端点要落在对边上.如下页图(2),AD, BE, CF是△ ABC的三条角平分线,则∠1=______, ∠3=
_______, ∠ACB= 2_______.
1知3-练∠2∠ABC∠4今天我们学了什么呢?
1.三角形的高、中线、角平分线等有关概念及它们
的画法.
2.三角形的高、中线、角平分线几何表达及简单应
用.完成教材P8T3、T4、P9T8、T9
