华师大 数学八年级上13.2.1全等三角形课件
文档属性
| 名称 | 华师大 数学八年级上13.2.1全等三角形课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 594.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-13 00:00:00 | ||
图片预览





文档简介
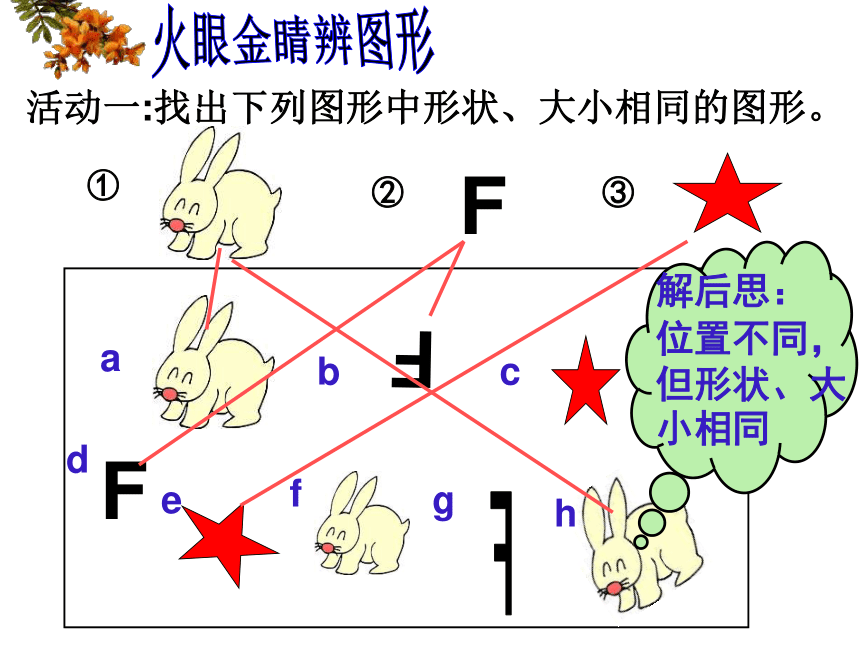
课件32张PPT。 全等三角形的判定13.2①②③火眼金睛辨图形活动一:找出下列图形中形状、大小相同的图形。FFFFadcbhgfe同一张底片洗出的照片能够完全重合的两个图形称为全等图形两张纸重合后剪纸,得到的两个图形大小、
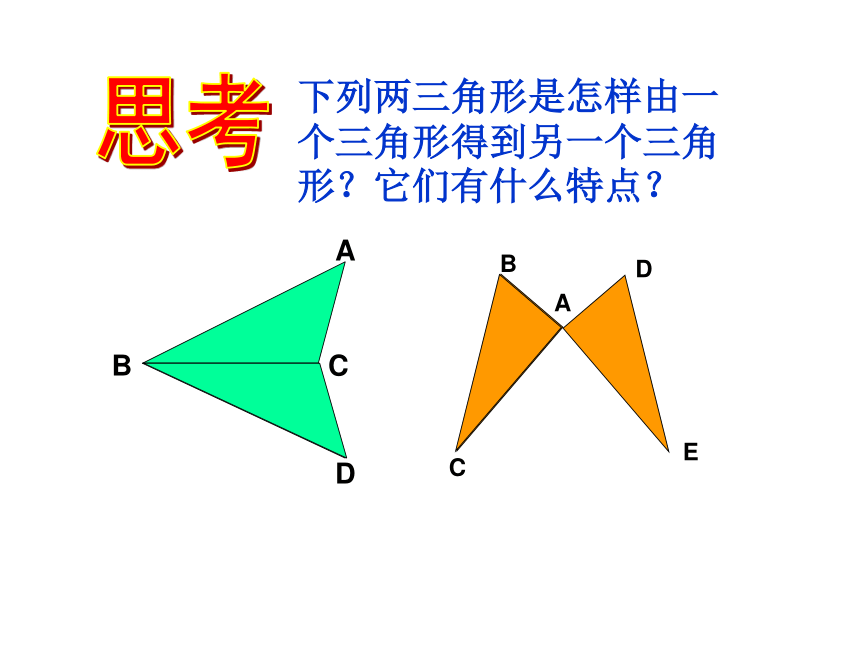
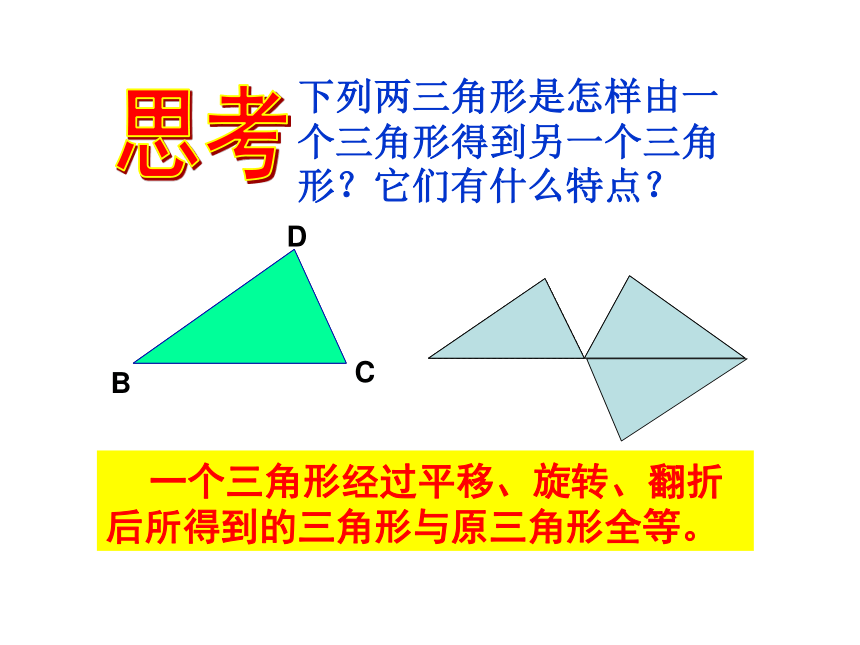
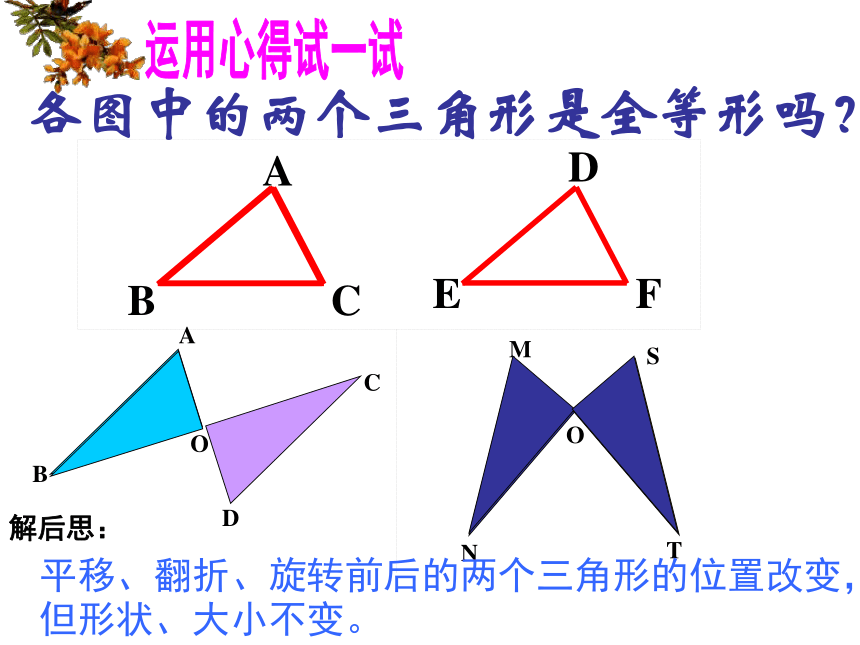
形状相同。下列两三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?思考ACBDE下列两三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?思考ABCDADE下列两三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?思考BDC 一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。ABCDEF各图中的两个三角形是全等形吗?运用心得试一试解后思:平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变。 1、能够完全重合的两个三角形,叫做 全等三角形.2、把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角
活动3、大家来掌握新知!3、全等三角形的表示法“全等”用符号“≌” 表示图中的△ABC△DEF全等,记作△ABC≌ △DEF,读作△ABC全等于△DEF记两个三角形全等时,
通常把表示对应顶点
的字母写在对应的位置
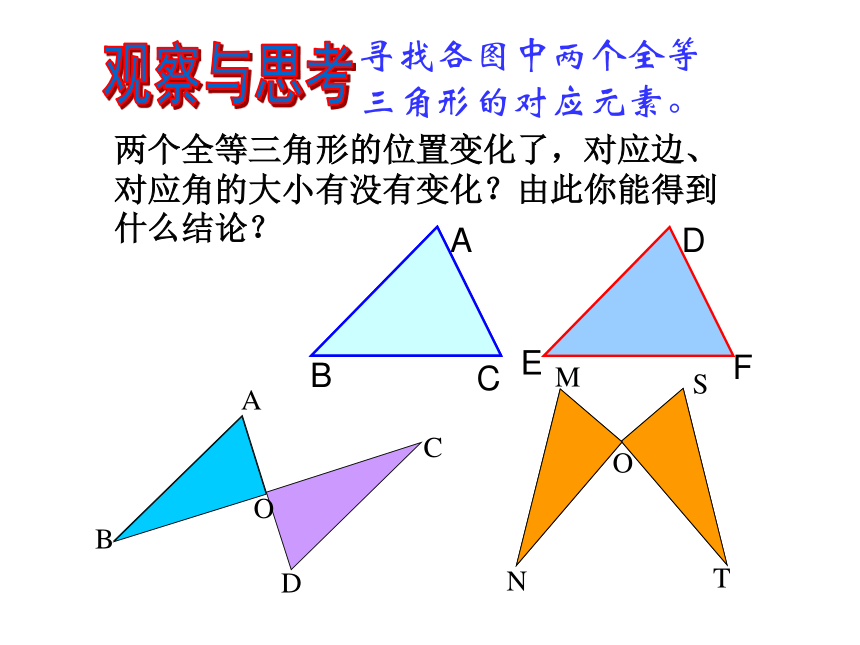
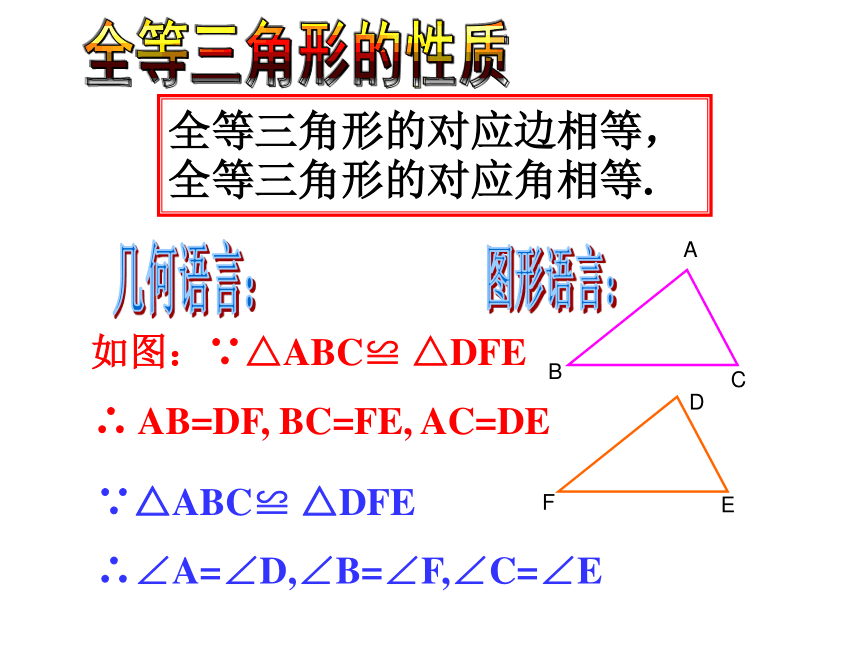
上。两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?寻找各图中两个全等三角形的对应元素。观察与思考EADCBF全等三角形的对应边相等,全等三角形的对应角相等. 如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE几何语言:∵△ABC≌ △DFE
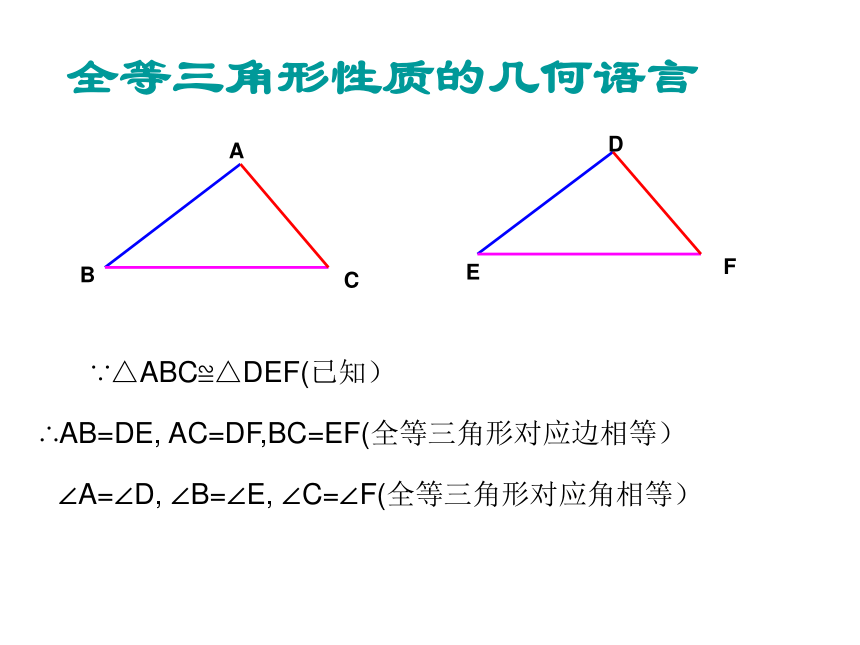
∴∠A=∠D,∠B=∠F,∠C=∠E图形语言:全等三角形的性质全等三角形性质的几何语言∵△ABC≌△DEF(已知)∴AB=DE, AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等)ABCDEF∵△ACB≌△DEF
∴AB=DF, CB=EF,AC=DE.∴∠A=∠D,∠CBA=∠F,∠C= ∠DEF. 先写出全等式,再指出它们的对应边和对应角探究交流ABCD∵△ABC≌△ABD∴AB=AB,BC=BD,AC=AD.∴∠BAC=∠BAD,∠ABC=∠ABD
∠C= ∠D.规律一:有公共边的,公共边是对应边 先写出全等式,再指出它们的对应边和对应角探究交流ACDB∵△AOC≌△BOD∴AO=BO,AC=BD,OC=OD.∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.规律二:有对顶角的,对顶角是对应角o 先写出全等式,再指出它们的对应边和对应角探究交流ABCDE∵△ABC≌△ADE∴AB=AD,AC=AE,
BC=DE∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.规律三:有公共角的,公共角是对应角先写出全等式,再指出它们的对应边和对应角探究交流 先写出全等式,再指出它们的对应边和对应角∵△ABC≌△FDE∴AB=FD,AC=FE,
BC=DE∴∠A=∠F,
∠B=∠D,
∠ACB= ∠FED.规律五:一对最大的角是对应角
一对最小的角是对应角ABCFDE规律四:一对最长的边是对应边
一对最短的边是对应边探究交流寻找对应边、对应角的规律
在全等三角形中,一般是:
1.有公共边,则公共边为对应边
2.有公共角,则公共角(对顶角)为对应角3.最大边与最大边(最小边与最小边) 为 对应边;最大角与最大角(最小角与最小角)为对应角找出下列全等三角形的对应边、对应角△AOB≌△DOC△ABC≌△DCBO课堂练习 1、若△AOC≌△BOD,AC=
∠A= ABOCD 2、若△ABD≌△ACE,BD= ,
∠BDA= 3、若△ABC≌△CDA,AB=
∠BAC=
请填空BD∠BCE∠CEACD∠DCA公共点公共角公共边(2)已知△ABC≌△CDA,
则AC边的对应边为(1)已知△ABC≌△ADE,
则∠A的对应角为(3)已知△ABC≌△DEF,
则AB边的对应边为
∠C的对应角为CA∠ADE∠F填一填:(4)如右图,已知△ABD≌△ACE, 且∠C=45°,AC = 8,AE = 5,则 ∠B = , DC = .45° 3 2、请选择 (1) △ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=6cm,BD=5cm,AD=7cm,那么BC的长是( )
(A)7cm (B)6cm (C)5cm ( D)无法确定
(2)在上题中, ∠CAB的对应角是( )
(A)∠DAB (B) ∠ DBA
(C) ∠ DBC (D) ∠ CAD AB如图, △ABD ≌ △EBC2、如果AB=3cm,BC=5cm, 求BE、BD的长. ∴BE=3cm,BD=5cm解:∵△ABD ≌ △EBC∴AB=EB,BC=BD∵AB=3cm,BC=5cm1、请找出对应边和对应角。 AB = EB、BC = BD、AD = EC,∠A=∠BEC、∠D=∠C、∠ABD=∠EBC课堂练习如图, △EFG≌△NMH2、如果EF=2.1cm,EH=1.1cm,
HN=3.3cm, 求NM、HG的长.∴HG=EG-HG=3.3-1.1=2.2解:∵△EFG ≌ △NMH∴NM=EF=2.1,EG=HN=3.31、请找出对应边和对应角。 课堂练习△ABD≌△ACE,若∠ADB=100°,∠B=30°,说出△ACE中各角的大小?解:∵ △ABD≌△ACE,
∴∠AEC= ∠ADB=1000 ,
∠C= ∠B=300,
又∵∠A+∠AEC+∠C=180°
∴∠A=1800- ∠AEC- ∠C
=1800-1000-300=500课堂练习互相重合的角叫做___互相重合的边叫做____ 其中:互相重合的顶点叫做___2. 叫全等三角形。1.能够重合的两个图形叫做 。全等形4.全等三角形的 和 相等对应边对应角对应顶点课 堂 小 结 能够完全重合的两个三角形3.“全等”用符号“ ”来表示,读作“ ”对应边对应角5.书写全等式时要求把对应字母放在对应的位置上全等于≌探究新知(一) (1)只给一个条件:一条边,大家画出三角形,小组交流画的三角形全等吗?一个角,大家画出三角形,小组交流画的三角形全等吗?1.一组对应边相等或一组对应角相等①一条边:②一个角:画一画:一组对应元素画一画:两组对应元素①一边一内角:②两内角:③两边:比较发现 1.小组的同学相互比较,所画的三角形是否全等.你们在比较过程中,能得出什么结论?2.我们会发现,如果只知道两个三角形有一组或两组分别对应相等(边或角),那么这两个三角形不一定全等(甚至形状都不相同)思考探究 议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
(有四种可能:三条边、三个角、两边一角和两角一边)
对于按以上每一种可能画得三角形是否全等,以后我们一起分别逐个探讨研究。
形状相同。下列两三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?思考ACBDE下列两三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?思考ABCDADE下列两三角形是怎样由一个三角形得到另一个三角形?它们有什么特点?思考BDC 一个三角形经过平移、旋转、翻折后所得到的三角形与原三角形全等。ABCDEF各图中的两个三角形是全等形吗?运用心得试一试解后思:平移、翻折、旋转前后的两个三角形的位置改变,但形状、大小不变。 1、能够完全重合的两个三角形,叫做 全等三角形.2、把两个全等的三角形重叠到一起时,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角
活动3、大家来掌握新知!3、全等三角形的表示法“全等”用符号“≌” 表示图中的△ABC△DEF全等,记作△ABC≌ △DEF,读作△ABC全等于△DEF记两个三角形全等时,
通常把表示对应顶点
的字母写在对应的位置
上。两个全等三角形的位置变化了,对应边、对应角的大小有没有变化?由此你能得到什么结论?寻找各图中两个全等三角形的对应元素。观察与思考EADCBF全等三角形的对应边相等,全等三角形的对应角相等. 如图:∵△ABC≌ △DFE
∴ AB=DF, BC=FE, AC=DE几何语言:∵△ABC≌ △DFE
∴∠A=∠D,∠B=∠F,∠C=∠E图形语言:全等三角形的性质全等三角形性质的几何语言∵△ABC≌△DEF(已知)∴AB=DE, AC=DF,BC=EF(全等三角形对应边相等)
∠A=∠D, ∠B=∠E, ∠C=∠F(全等三角形对应角相等)ABCDEF∵△ACB≌△DEF
∴AB=DF, CB=EF,AC=DE.∴∠A=∠D,∠CBA=∠F,∠C= ∠DEF. 先写出全等式,再指出它们的对应边和对应角探究交流ABCD∵△ABC≌△ABD∴AB=AB,BC=BD,AC=AD.∴∠BAC=∠BAD,∠ABC=∠ABD
∠C= ∠D.规律一:有公共边的,公共边是对应边 先写出全等式,再指出它们的对应边和对应角探究交流ACDB∵△AOC≌△BOD∴AO=BO,AC=BD,OC=OD.∴∠A=∠B,∠C=∠D,
∠AOC= ∠BOD.规律二:有对顶角的,对顶角是对应角o 先写出全等式,再指出它们的对应边和对应角探究交流ABCDE∵△ABC≌△ADE∴AB=AD,AC=AE,
BC=DE∴∠A=∠A,∠B=∠D,
∠ACB= ∠AED.规律三:有公共角的,公共角是对应角先写出全等式,再指出它们的对应边和对应角探究交流 先写出全等式,再指出它们的对应边和对应角∵△ABC≌△FDE∴AB=FD,AC=FE,
BC=DE∴∠A=∠F,
∠B=∠D,
∠ACB= ∠FED.规律五:一对最大的角是对应角
一对最小的角是对应角ABCFDE规律四:一对最长的边是对应边
一对最短的边是对应边探究交流寻找对应边、对应角的规律
在全等三角形中,一般是:
1.有公共边,则公共边为对应边
2.有公共角,则公共角(对顶角)为对应角3.最大边与最大边(最小边与最小边) 为 对应边;最大角与最大角(最小角与最小角)为对应角找出下列全等三角形的对应边、对应角△AOB≌△DOC△ABC≌△DCBO课堂练习 1、若△AOC≌△BOD,AC=
∠A= ABOCD 2、若△ABD≌△ACE,BD= ,
∠BDA= 3、若△ABC≌△CDA,AB=
∠BAC=
请填空BD∠BCE∠CEACD∠DCA公共点公共角公共边(2)已知△ABC≌△CDA,
则AC边的对应边为(1)已知△ABC≌△ADE,
则∠A的对应角为(3)已知△ABC≌△DEF,
则AB边的对应边为
∠C的对应角为CA∠ADE∠F填一填:(4)如右图,已知△ABD≌△ACE, 且∠C=45°,AC = 8,AE = 5,则 ∠B = , DC = .45° 3 2、请选择 (1) △ABC≌ △BAD,点A和点B、点C和点D是对应点,如果AB=6cm,BD=5cm,AD=7cm,那么BC的长是( )
(A)7cm (B)6cm (C)5cm ( D)无法确定
(2)在上题中, ∠CAB的对应角是( )
(A)∠DAB (B) ∠ DBA
(C) ∠ DBC (D) ∠ CAD AB如图, △ABD ≌ △EBC2、如果AB=3cm,BC=5cm, 求BE、BD的长. ∴BE=3cm,BD=5cm解:∵△ABD ≌ △EBC∴AB=EB,BC=BD∵AB=3cm,BC=5cm1、请找出对应边和对应角。 AB = EB、BC = BD、AD = EC,∠A=∠BEC、∠D=∠C、∠ABD=∠EBC课堂练习如图, △EFG≌△NMH2、如果EF=2.1cm,EH=1.1cm,
HN=3.3cm, 求NM、HG的长.∴HG=EG-HG=3.3-1.1=2.2解:∵△EFG ≌ △NMH∴NM=EF=2.1,EG=HN=3.31、请找出对应边和对应角。 课堂练习△ABD≌△ACE,若∠ADB=100°,∠B=30°,说出△ACE中各角的大小?解:∵ △ABD≌△ACE,
∴∠AEC= ∠ADB=1000 ,
∠C= ∠B=300,
又∵∠A+∠AEC+∠C=180°
∴∠A=1800- ∠AEC- ∠C
=1800-1000-300=500课堂练习互相重合的角叫做___互相重合的边叫做____ 其中:互相重合的顶点叫做___2. 叫全等三角形。1.能够重合的两个图形叫做 。全等形4.全等三角形的 和 相等对应边对应角对应顶点课 堂 小 结 能够完全重合的两个三角形3.“全等”用符号“ ”来表示,读作“ ”对应边对应角5.书写全等式时要求把对应字母放在对应的位置上全等于≌探究新知(一) (1)只给一个条件:一条边,大家画出三角形,小组交流画的三角形全等吗?一个角,大家画出三角形,小组交流画的三角形全等吗?1.一组对应边相等或一组对应角相等①一条边:②一个角:画一画:一组对应元素画一画:两组对应元素①一边一内角:②两内角:③两边:比较发现 1.小组的同学相互比较,所画的三角形是否全等.你们在比较过程中,能得出什么结论?2.我们会发现,如果只知道两个三角形有一组或两组分别对应相等(边或角),那么这两个三角形不一定全等(甚至形状都不相同)思考探究 议一议
如果给出三个条件画三角形,你能说出有哪几种可能的情况?
(有四种可能:三条边、三个角、两边一角和两角一边)
对于按以上每一种可能画得三角形是否全等,以后我们一起分别逐个探讨研究。
