2.2.1平行四边形的性质(课件+教案+学案+微课)
文档属性
| 名称 | 2.2.1平行四边形的性质(课件+教案+学案+微课) | 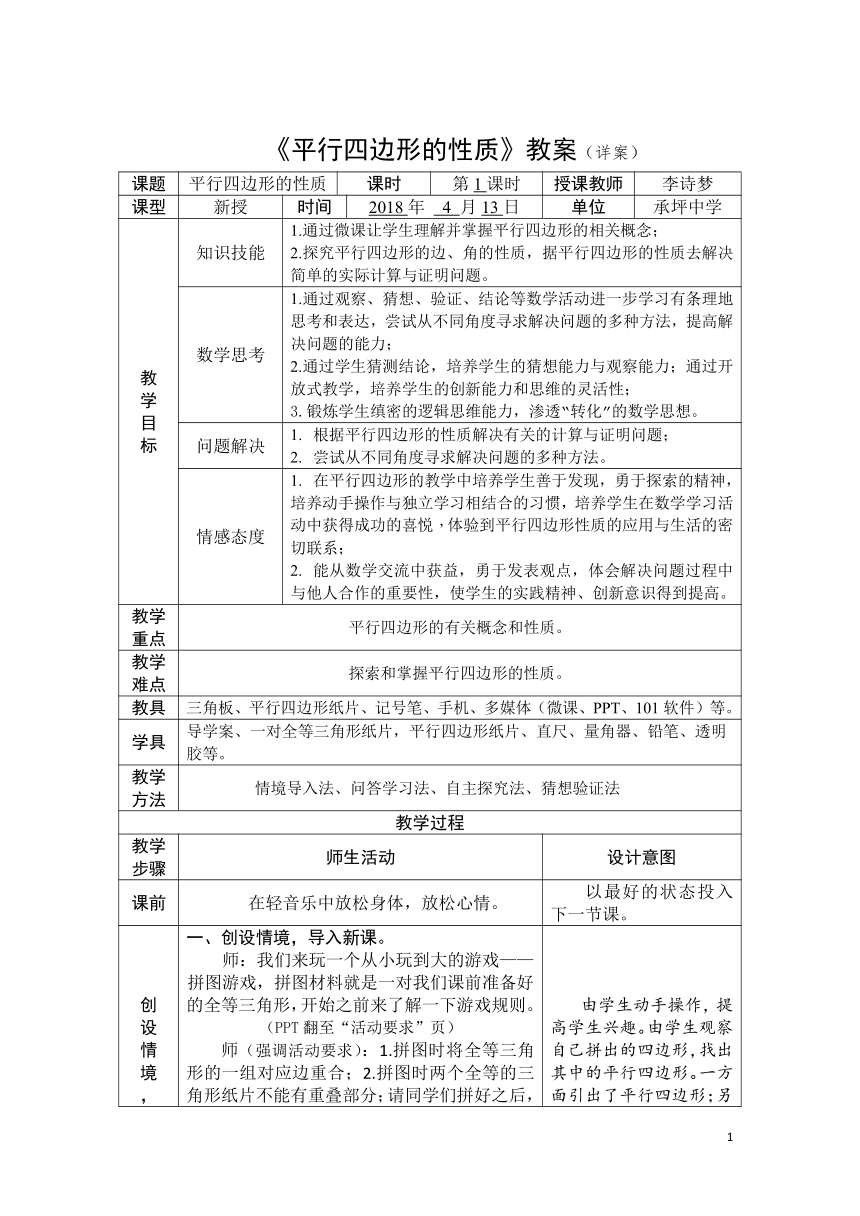 | |
| 格式 | zip | ||
| 文件大小 | 32.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-14 20:31:38 | ||
图片预览



文档简介
《平行四边形的性质》教案(详案)
课题
平行四边形的性质
课时
第1课时
授课教师
李诗梦
课型
新授
时间
2018年 4 月13日
单位
承坪中学
教
学
目
标
知识技能
1.通过微课让学生理解并掌握平行四边形的相关概念;
2.探究平行四边形的边、角的性质,据平行四边形的性质去解决简单的实际计算与证明问题。
数学思考
1.通过观察、猜想、验证、结论等数学活动进一步学习有条理地思考和表达,尝试从不同角度寻求解决问题的多种方法,提高解决问题的能力;
2.通过学生猜测结论,培养学生的猜想能力与观察能力;通过开放式教学,培养学生的创新能力和思维的灵活性;
3.锻炼学生缜密的逻辑思维能力,渗透“转化”的数学思想。
问题解决
根据平行四边形的性质解决有关的计算与证明问题;
尝试从不同角度寻求解决问题的多种方法。
情感态度
在平行四边形的教学中培养学生善于发现,勇于探索的精神,培养动手操作与独立学习相结合的习惯,培养学生在数学学习活动中获得成功的喜悦,体验到平行四边形性质的应用与生活的密切联系;
能从数学交流中获益,勇于发表观点,体会解决问题过程中与他人合作的重要性,使学生的实践精神、创新意识得到提高。
教学
重点
平行四边形的有关概念和性质。
教学
难点
探索和掌握平行四边形的性质。
教具
三角板、平行四边形纸片、记号笔、手机、多媒体(微课、PPT、101软件)等。
学具
导学案、一对全等三角形纸片,平行四边形纸片、直尺、量角器、铅笔、透明胶等。
教学方法
情境导入法、问答学习法、自主探究法、猜想验证法
教学过程
教学
步骤
师生活动
设计意图
课前
在轻音乐中放松身体,放松心情。
以最好的状态投入下一节课。
创
设
情
境
,
导
入
新
课
一、创设情境,导入新课。
师:我们来玩一个从小玩到大的游戏——拼图游戏,拼图材料就是一对我们课前准备好的全等三角形,开始之前来了解一下游戏规则。(PPT翻至“活动要求”页)
师(强调活动要求):1.拼图时将全等三角形的一组对应边重合;2.拼图时两个全等的三角形纸片不能有重叠部分;请同学们拼好之后,用透明胶黏上,并以最快的速度将其粘贴在黑板自己小组的位置。两分钟以内,比一比,哪个小组拼出的图形最多?
(学生拼图并将成果粘贴在黑板上。)
师:每个小组都发挥出了集体的智慧,拼出了不同的图形,真好!
师(选取其中的一个平行四边形):这个四边形像我们小学学过的哪种图形?
生:平行四边形
师:这节课我们就一起来研究平行四边形。
由学生动手操作,提高学生兴趣。由学生观察自己拼出的四边形,找出其中的平行四边形。一方面引出了平行四边形;另一方面这个拼图过程为后面学生证明它的性质奠定基础(即将平行四边形转化为2个三角形)。
二、微课引路,求索新知
1.观看微课,了解平行四边形。
师:让我们通过微课来进一步认识平行四边形吧。认真,仔细,可不要错过重点。看完,我可是会提问题的。
(学生观看微课)
师:谁来说一说平行四边形的定义是什么?
生:两组对边分别平行的四边形叫做平行四边形。
师:非常准确,说明你很认真。
师(强调定义并板书):两组对边分别平行的四边形叫做平行四边形。我们一起来齐读一遍。两组......预备起......。
(学生齐读定义)
2.分类活动,巩固定义。
师:黑板上这么多的图形,根据平行四边形的定义,哪些是平行四边形呢?请每组派一名代表,将你们小组的拼的平行四边形找出来贴在右边的黑板上。
(6名代表将平行四边形粘贴在黑板右边)
师:下面的同学也要擦亮眼睛,看看自己组的是不是拿对了,别组的有没有拿对。
(学生完成分类)
师:认真观察,是不是按要求取的图形,平行四边形都拿出来了吗?
情况一:
生:都拿对了。
师:非常棒,说明你们掌握了定义。
情况二:
生:第x组不对。
师:为什么?
生:因为矩形、正方形都是特殊的平行四边形。
师:依据是什么?
生:两组对边分别平行
师:非常棒!定义掌握的非常好,也非常善于思考。掌声鼓励。
师:现在我们稍作休息30s,从兴奋的状态中沉浸下来,因为下面我们的重头戏来了。
(音乐30s)
师:时间到。
活动体验,性质探究
师:请认真思考老师提出的问题,从平行四边形的定义中,我们可以得出平行四边形的什么性质?请一位同学来回答。
生:两组对边分别平行
师:嗯,不错。请坐!
师:那除此之外,平行四边形还有什么样的性质呢?现在,我们就一起来研究平行四边形边、角的性质。
师:我们把桌面上的平行四边形拿出来,请你认真仔细观察,并大胆猜测,平行四边行的边和角有什么样的性质呢?相互之间可以进行讨论,并把你的猜测写在导学案的相应位置。
(学生观察、讨论,并将猜测写下来)
师;请一位同学来说一说。回答:我猜测平行四边形的......
生:我猜测平行四边形的对边相等,对角也相等。
师:嗯,非常大胆的猜测。有没有谁的猜测与他不一样?或者有补充?
生:没有
师:那怎么才能验证你的猜想呢?可以用什么方法?(示意学生举手)
方法一:
生:可以将平行四边形剪开,然后拼在一起对比一下,重合就代表相等。
师:这个方法简单、直观,不错。
方法二:
生:可以测量边和角的长度
师:你说的就是测量法,用数据说话,这个方法不错。
方法三:
生:推理证明
师:说得好!我都忍不住为你鼓掌。这个方法非常严谨。
师:现在就让我们一起从测量法开始探究平行四边形边、角的性质吧。
师:请从课间准备的平行四边形中任取三个,每一个平行四边形依次标记顶点A、B、C、D。
(教师拿出三个平行四边形示范标记顶点,学生跟着老师一起标记)
师:再为平行四边行依次标记①、②、③.(示范标记)
师:请全班同学读一遍这一页PPT。
(学生齐读)
师:开始!
(学生动手实践,教师走动指导)
师:时间到!现在哪组愿意派出一位代表来讲台上分析你们的数据,说出你们的结论。
生1:我们这组得出的结论是平行四边形的对边相等,平行四边形的对角相等。因为......
师:你们的结论都一样吗?有没有不同的?或者还有另外的发现。有,就大胆说出来!
师:其实还有,但是呢!留给你们课后去讨论。
师:老师在实验过程中,发现你们都很棒,组内分工明确,齐心协力,都有着一双善于发现的眼睛和善于思考的大脑。其实,在数学学科中,测量得出来的结论还不够严谨,我们要用严谨的理论知识来进行验证,才能下结论。
方法三:推理证明
师:第三个方法:推理证明。以我们刚才得到的一个命题是“平行四边形的对边,对角相等”为例。我们来证明它是个真命题,还是假命题。
证明图形有关的命题,有三步:
第一步:根据题意,画出图形。我已经为你们画好了。
第二步:写出已知求证
已知:四边形ABCD是平行四边形
求证:AB=CD AD=BC
第三部:证明。如何证明呢?想一想。
情况一:
(学生没反应)
师:还记我们最开始玩过的拼图游戏吗?有没有什么启发。
情况二:
生:做对角线。
师:为什么要做对角线?你的想法是?
生:构造两个全等的三角形。
师:非常不错,一条对角线,你将平行四边形的问题转化为三角形的问题,将未知转化为了已知来解决。运用到了数学的“转化”思想。
师:那么如何证明两个三角形全等呢?为了使得过程更加清晰仔细,我为这几个角依次标记。
师:证明这两个三角形全等,需要什么条件呢?谁来说一说。
师:有没有对应角相等呢?
生:有
师:哪对?
生:∠1=∠2
师:理由?
生:四边形ABCD是平行四边形,AB平行于DC,,两直线平行,内错角相等(教师根据学生的回答板书)
师:还有哪一组对应角相等?
生:3=4
师:理由?
生:AD平行于BC,,两直线平行,内错角相等。(板书)
师:除此之外,有没有那组对应边相等?
生:AC=CA
师:为什么?
生:公共边(板书)
师:由此我们就证明了三角形ABC全等于三角形CDA,所以AB=DC,AD=BC,B=D
师:还有一组角呀?怎么办?
生:因为BAD+B=180 ,BCD+D=180
所以BAD=BCD
师:经过严谨的证明,我们终于能够有底气自信满满的说出平行四边形的性质了。
平行四边形的对边相等,
平行四边形的对角相等。(板书)
师:我们一起齐读两遍
(生齐读)
全面探究本课教学实质,以简单明了的形式,突出平行四边形的两个重要性质,从重叠、对比的角度让学生亲身经历探究过程,体验数量与位置关系的实质,使学生深刻地理解,全面地掌握.
师:趁热打铁,我们它运用起来解决实际问题吧。(显示PPT)
实现训练与检测同步,及时反馈学习情况,有利于学生查漏补缺,有利于教师针对性地补充未讲到的内容.
师总结:你们今天都非常的了不起,你们通过认真观察,然后大胆的猜测,想方设法来验证,最后得出结论。了不起。在数学的天地里,重要的不是我们知道什么,而是怎么知道。老师与同学们共勉。好,今天的课就到这儿。下课!
板书设计
教学反思
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
