2009届高考百所名校模拟精华重组卷物理2)新课标卷
文档属性
| 名称 | 2009届高考百所名校模拟精华重组卷物理2)新课标卷 |  | |
| 格式 | rar | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2009-05-08 04:47:00 | ||
图片预览



文档简介
2009届高考百所名校模拟精华重组卷物理(二)新课标卷
第Ⅰ卷 (选择题 共48分)
一、选择题(本题包括8小题。每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得6分,选对但不全的得3分,有选错或不答的得0分)
【1】如图所示电路与一绝热密闭汽缸相连,Ra为电热丝,汽缸内有一定质量的理想气体,闭合电键后,汽缸里的气体
A、内能增大
B、平均动能减小
C、无规则热运动增强
D、单位时间内对单位面积器壁的撞击次数减少
【2】如图所示,位于介质Ⅰ和Ⅱ分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波。若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则
A、f1=2f2 v1=v2
B、f1=f2 v1=2v2
C、f1=f2 v1=0.5v2
D、f1=0.5f2 v1=v2
【3】若规定氢原子处于基态时的能量为E1=0,则其它各激发态的能量依次为E2=10.2eV、E3=12.09eV、E4=12.75eV、E5=13.06eV、……。在气体放电管中,处于基态的氢原子受到能量为12.8eV的高速电子轰击而跃迁到激发态,在这些氢原子从激发态向低能级跃迁的过程中(AC)
A.总共能辐射出六种不同频率的光子
B.总共能辐射出十种不同频率的光子
C.辐射出波长最长的光子是从n=4跃迁到n=3能级时放出的
D.辐射出波长最长的光子是从n=5跃迁到n=4能级时放出的
【4】如图所示,水平面上停放着A、B两辆小车,质量分别为M和m,M>m,两车相距为L。人的质量也为m,另有不计质量的一根硬杆和一根细绳。第一次人站在A车上,杆插在B车上;第二次人站在B车上,杆插在A车上。两种情况下,人用同样大小的力拉绳子,使两车相遇。设阻力可忽略不计,两次小车从开始运动到相遇的时间分别为t1和t2,则 A、t1=t2
B、t1<t2
C、t1>t2
D、条件不足,无法判断
【5】太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球公转速度的7倍,轨道半径约为地球公转轨道半径的2×109倍。为了粗略估算银河系中恒星的数目,可认为银河系中所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳质量,则银河系中恒星数目约为
A、1015 B、1013 C、1011 D、109
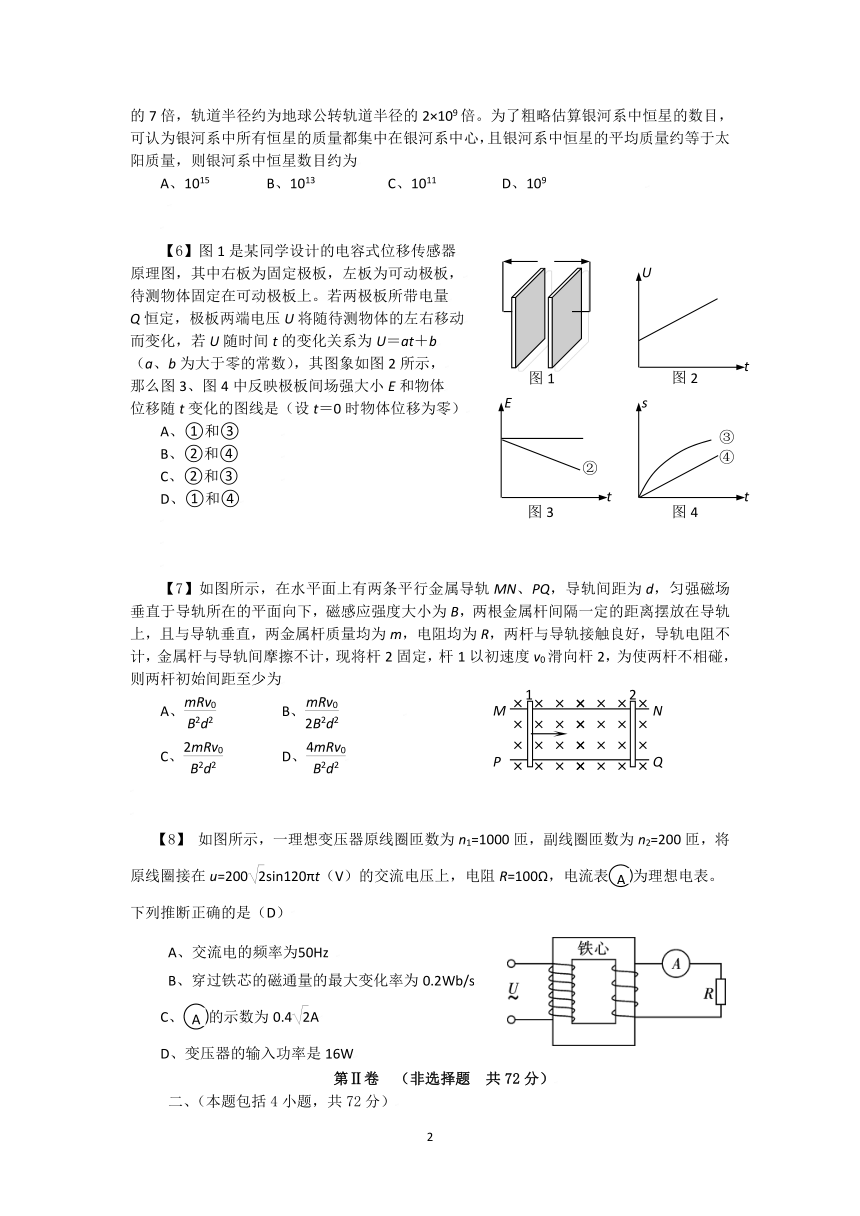
【6】图1是某同学设计的电容式位移传感器
原理图,其中右板为固定极板,左板为可动极板,
待测物体固定在可动极板上。若两极板所带电量
Q恒定,极板两端电压U将随待测物体的左右移动
而变化,若U随时间t的变化关系为U=at+b
(a、b为大于零的常数),其图象如图2所示,
那么图3、图4中反映极板间场强大小E和物体
位移随t变化的图线是(设t=0时物体位移为零)
A、①和③
B、②和④
C、②和③
D、①和④
【7】如图所示,在水平面上有两条平行金属导轨MN、PQ,导轨间距为d,匀强磁场垂直于导轨所在的平面向下,磁感应强度大小为B,两根金属杆间隔一定的距离摆放在导轨上,且与导轨垂直,两金属杆质量均为m,电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆与导轨间摩擦不计,现将杆2固定,杆1以初速度v0滑向杆2,为使两杆不相碰,则两杆初始间距至少为
A、 B、
C、 D、
【8】 如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200sin120πt(V)的交流电压上,电阻R=100Ω,电流表为理想电表。下列推断正确的是(D)
A、交流电的频率为50Hz
B、穿过铁芯的磁通量的最大变化率为0.2Wb/s
C、的示数为0.4A
D、变压器的输入功率是16W
第Ⅱ卷 (非选择题 共72分)
二、(本题包括4小题,共72分)
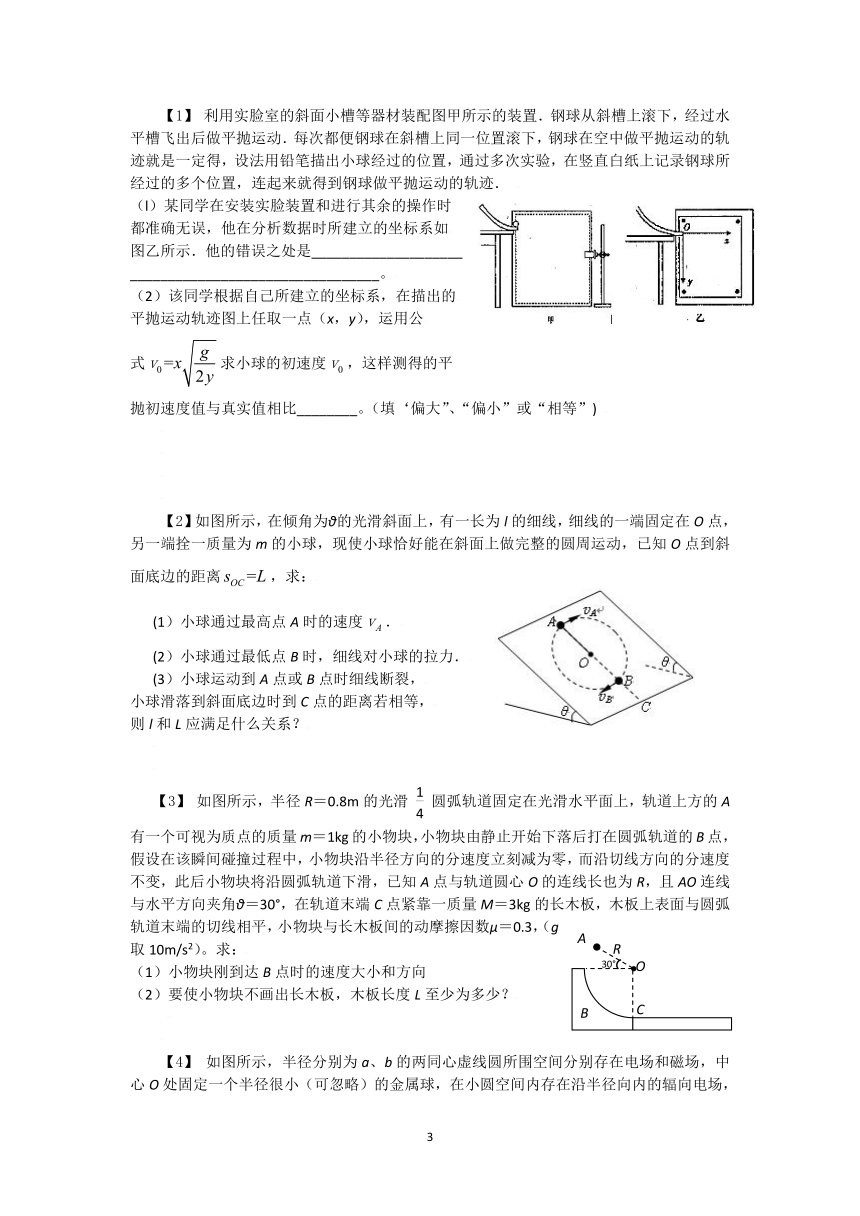
【1】 利用实脸室的斜面小槽等器材装配图甲所示的装置.钢球从斜槽上滚下,经过水平槽飞出后做平抛运动.每次都便钢球在斜槽上同一位置滚下,钢球在空中做平抛运动的轨迹就是一定得,设法用铅笔描出小球经过的位置,通过多次实验,在竖直白纸上记录钢球所经过的多个位置,连起来就得到钢球做平抛运动的轨迹.
(l)某同学在安装实脸装置和进行其余的操作时
都准确无误,他在分析数据时所建立的坐标系如
图乙所示.他的错误之处是____________________
_________________________________。
(2)该同学根据自己所建立的坐标系,在描出的
平抛运动轨迹图上任取一点(x,y),运用公
式求小球的初速度,这样测得的平
抛初速度值与真实值相比________。(填‘偏大”、“偏小”或“相等”)
【2】如图所示,在倾角为θ的光滑斜面上,有一长为l的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在斜面上做完整的圆周运动,已知O点到斜面底边的距离,求:
(1)小球通过最高点A时的速度.
(2)小球通过最低点B时,细线对小球的拉力.
(3)小球运动到A点或B点时细线断裂,
小球滑落到斜面底边时到C点的距离若相等,
则l和L应满足什么关系?
【3】 如图所示,半径R=0.8m的光滑 圆弧轨道固定在光滑水平面上,轨道上方的A有一个可视为质点的质量m=1kg的小物块,小物块由静止开始下落后打在圆弧轨道的B点,假设在该瞬间碰撞过程中,小物块沿半径方向的分速度立刻减为零,而沿切线方向的分速度不变,此后小物块将沿圆弧轨道下滑,已知A点与轨道圆心O的连线长也为R,且AO连线与水平方向夹角θ=30°,在轨道末端C点紧靠一质量M=3kg的长木板,木板上表面与圆弧轨道末端的切线相平,小物块与长木板间的动摩擦因数μ=0.3,(g取10m/s2)。求:
(1)小物块刚到达B点时的速度大小和方向
(2)要使小物块不画出长木板,木板长度L至少为多少?
【4】 如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求:
(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B。
(3)若磁感应强度取(2)中最小值,且b=(+1)a,要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间。(设粒子与金属球正碰后电量不变且能以原速率原路返回)
答案解析:
第Ⅰ卷 (选择题 共48分)
一、选择题(本题包括8小题。每小题给出的四个选项中,有的只有一个选项正确,有的有多个选项正确,全部选对的得6分,选对但不全的得3分,有选错或不答的得0分)
【1】如图所示电路与一绝热密闭汽缸相连,Ra为电热丝,汽缸内有一定质量的理想气体,闭合电键后,汽缸里的气体
A、内能增大
B、平均动能减小
C、无规则热运动增强
D、单位时间内对单位面积器壁的撞击次数减少
【2】如图所示,位于介质Ⅰ和Ⅱ分界面上的波源S,产生两列分别沿x轴负方向与正方向传播的机械波。若在两种介质中波的频率及传播速度分别为f1、f2和v1、v2,则
A、f1=2f2 v1=v2
B、f1=f2 v1=2v2
C、f1=f2 v1=0.5v2
D、f1=0.5f2 v1=v2
【3】若规定氢原子处于基态时的能量为E1=0,则其它各激发态的能量依次为E2=10.2eV、E3=12.09eV、E4=12.75eV、E5=13.06eV、……。在气体放电管中,处于基态的氢原子受到能量为12.8eV的高速电子轰击而跃迁到激发态,在这些氢原子从激发态向低能级跃迁的过程中(AC)
A.总共能辐射出六种不同频率的光子
B.总共能辐射出十种不同频率的光子
C.辐射出波长最长的光子是从n=4跃迁到n=3能级时放出的
D.辐射出波长最长的光子是从n=5跃迁到n=4能级时放出的
【4】如图所示,水平面上停放着A、B两辆小车,质量分别为M和m,M>m,两车相距为L。人的质量也为m,另有不计质量的一根硬杆和一根细绳。第一次人站在A车上,杆插在B车上;第二次人站在B车上,杆插在A车上。两种情况下,人用同样大小的力拉绳子,使两车相遇。设阻力可忽略不计,两次小车从开始运动到相遇的时间分别为t1和t2,则 A、t1=t2
B、t1<t2
C、t1>t2
D、条件不足,无法判断
【5】太阳围绕银河系中心的运动可视为匀速圆周运动,其运动速度约为地球公转速度的7倍,轨道半径约为地球公转轨道半径的2×109倍。为了粗略估算银河系中恒星的数目,可认为银河系中所有恒星的质量都集中在银河系中心,且银河系中恒星的平均质量约等于太阳质量,则银河系中恒星数目约为
A、1015 B、1013 C、1011 D、109
【6】图1是某同学设计的电容式位移传感器
原理图,其中右板为固定极板,左板为可动极板,
待测物体固定在可动极板上。若两极板所带电量
Q恒定,极板两端电压U将随待测物体的左右移动
而变化,若U随时间t的变化关系为U=at+b
(a、b为大于零的常数),其图象如图2所示,
那么图3、图4中反映极板间场强大小E和物体
位移随t变化的图线是(设t=0时物体位移为零)
A、①和③
B、②和④
C、②和③
D、①和④
【7】如图所示,在水平面上有两条平行金属导轨MN、PQ,导轨间距为d,匀强磁场垂直于导轨所在的平面向下,磁感应强度大小为B,两根金属杆间隔一定的距离摆放在导轨上,且与导轨垂直,两金属杆质量均为m,电阻均为R,两杆与导轨接触良好,导轨电阻不计,金属杆与导轨间摩擦不计,现将杆2固定,杆1以初速度v0滑向杆2,为使两杆不相碰,则两杆初始间距至少为
A、 B、
C、 D、
【8】 如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200sin120πt(V)的交流电压上,电阻R=100Ω,电流表为理想电表。下列推断正确的是(D)
A、交流电的频率为50Hz
B、穿过铁芯的磁通量的最大变化率为0.2Wb/s
C、的示数为0.4A
D、变压器的输入功率是16W
第Ⅱ卷 (非选择题 共72分)
二、(本题包括4小题,共72分)
【1】 利用实脸室的斜面小槽等器材装配图甲所示的装置.钢球从斜槽上滚下,经过水平槽飞出后做平抛运动.每次都便钢球在斜槽上同一位置滚下,钢球在空中做平抛运动的轨迹就是一定得,设法用铅笔描出小球经过的位置,通过多次实验,在竖直白纸上记录钢球所经过的多个位置,连起来就得到钢球做平抛运动的轨迹.
(l)某同学在安装实脸装置和进行其余的操作时
都准确无误,他在分析数据时所建立的坐标系如
图乙所示.他的错误之处是____________________
_________________________________。
(2)该同学根据自己所建立的坐标系,在描出的
平抛运动轨迹图上任取一点(x,y),运用公
式求小球的初速度,这样测得的平
抛初速度值与真实值相比________。(填‘偏大”、“偏小”或“相等”)
【2】如图所示,在倾角为θ的光滑斜面上,有一长为l的细线,细线的一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在斜面上做完整的圆周运动,已知O点到斜面底边的距离,求:
(1)小球通过最高点A时的速度.
(2)小球通过最低点B时,细线对小球的拉力.
(3)小球运动到A点或B点时细线断裂,
小球滑落到斜面底边时到C点的距离若相等,
则l和L应满足什么关系?
【3】 如图所示,半径R=0.8m的光滑 圆弧轨道固定在光滑水平面上,轨道上方的A有一个可视为质点的质量m=1kg的小物块,小物块由静止开始下落后打在圆弧轨道的B点,假设在该瞬间碰撞过程中,小物块沿半径方向的分速度立刻减为零,而沿切线方向的分速度不变,此后小物块将沿圆弧轨道下滑,已知A点与轨道圆心O的连线长也为R,且AO连线与水平方向夹角θ=30°,在轨道末端C点紧靠一质量M=3kg的长木板,木板上表面与圆弧轨道末端的切线相平,小物块与长木板间的动摩擦因数μ=0.3,(g取10m/s2)。求:
(1)小物块刚到达B点时的速度大小和方向
(2)要使小物块不画出长木板,木板长度L至少为多少?
【4】 如图所示,半径分别为a、b的两同心虚线圆所围空间分别存在电场和磁场,中心O处固定一个半径很小(可忽略)的金属球,在小圆空间内存在沿半径向内的辐向电场,小圆周与金属球间电势差为U,两圆之间的空间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿+x轴方向以很小的初速度逸出,粒子质量为m,电量为q,(不计粒子重力,忽略粒子初速度)求:
(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强度超过某一临界值时,粒子将不能到达大圆周,求此最小值B。
(3)若磁感应强度取(2)中最小值,且b=(+1)a,要粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间。(设粒子与金属球正碰后电量不变且能以原速率原路返回)
答案解析:
同课章节目录
