12.11勾股定理课件 (共20张PPT)
文档属性
| 名称 | 12.11勾股定理课件 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 662.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-14 14:18:05 | ||
图片预览








文档简介
课件20张PPT。八年级上册12.11 勾股定理 认识勾股定理,利用勾股定理进行简单的计算和实际运用; 掌握勾股定理的验证,体会数形结合的思想和.121. 如果直角三角形两直角边长分别为 BC=5厘米 , AC=12厘米,求斜边AB的长度.
解:在Rt△ABC中,根据勾股定理,
AC2+BC2=AB2,
∵AC=12,BC=5
∴122+52=AB2.
∴AB2=169.
∴AB=13.
答:斜边AB的长度为13厘米 .2.已知一个直角三角形的两条直角边分别为6cm,8cm,那么这个直角三角形的斜边长为__________cm,斜边上的高为_______cm.
3.如图所示,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行_______米.10104.8据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你知道为什么吗? 用圆规和刻度尺作以下三个直角三角形.使它们的两条直角边分别为3cm,4cm;6cm,8cm;5cm,12cm.然后用刻度尺量出它们斜边的长. 我们发现,它们的斜边长分别为5cm,10cm和13cm. 你能从3cm,4cm,5cm;6cm,8cm,10cm;5cm,12cm, 13cm这三组数据中发现什么规律吗?我们看到:
32+42=52,62+82=102,52+122=132.由此可以猜想出:
在直角三角形中,斜边的平方等于两条直角边的平方和. 以上规律很早就被我国古代劳动人民发现了,他们把直角三角形较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.如图,在△ABC中,∠C=90°,那么
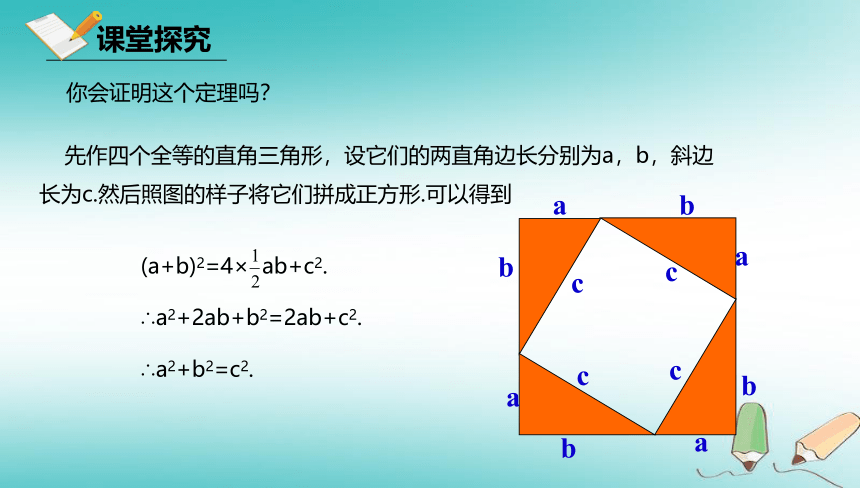
a2+b2=c2.勾股弦你会证明这个定理吗? 先作四个全等的直角三角形,设它们的两直角边长分别为a,b,斜边长为c.然后照图的样子将它们拼成正方形.可以得到(a+b)2=4× ab+c2.
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.例1、如图,一颗大树被大风刮到,折断的一段恰好落在地面上的A处,量得BC=5cm,AC=10cm.试计算这颗大树的高度(结果精确到1m).解:在直角三角形ABC中,
∵∠ACB=90°,
∴BC2+AC2=AB2(勾股定理).
∴AB2=52+102=125.
∴AB≈11(m).
树高=AB+BC≈16(m).
答:这棵树约有16m高.某养殖场有一个长2米、宽1.5米的长方形栅栏,现要在相对角的顶点间加固一条木板(木板的宽度忽略不计),则木板的长度应取_________米.2.5例2、已知:Rt△ABC中,∠C=90°,AB=8,BC= .求AC.解:在Rt△ABC中,
∵ ∠C=90°,
∴BC2+AC2=AB2(勾股定理).
∴AC2=82-( )2=46.
∴AC= .如图,有一个圆柱,它的高等于12cm,底面圆的周长为18cm,在圆柱下底面的A点有一只蚂蚁,它想吃到地面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?(1)在你自己做的圆柱上,尝试从点A到点B沿圆
柱侧面画几条路线,你觉得哪条路线最短?(2)如图,将圆柱侧面剪开展成一个长方形,点
A到点B的最短路线是什么?你画对了吗?(B)(3)蚂蚁从点A出发,想吃到B点上的食物,它沿
圆柱侧面爬行的最短路程是多少?12厘米9厘米AB2=122+92AB=15(厘米)1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A.600米 B.800米 C.1000米 D.不能确定
C2、如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.
求:四边形ABCD的面积.解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25,
∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD 3.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?解:设伸入油桶中的长度为 x 米,则最长时:x2=1.52+22,x=2.5.
∴最长是2.5+0.5=3(米)
最短时:x=1.5.
∴最短是1.5+0.5=2(米)
答:这根铁棒的长应在2~3米之间.1、勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
2、 “勾股定理”的应用:
已知直角三角形两边,求第三边.
3.在寻求最短路径时,往往把空间问题平面化,利用勾股定理及其逆定理解决实际问题.转化
解:在Rt△ABC中,根据勾股定理,
AC2+BC2=AB2,
∵AC=12,BC=5
∴122+52=AB2.
∴AB2=169.
∴AB=13.
答:斜边AB的长度为13厘米 .2.已知一个直角三角形的两条直角边分别为6cm,8cm,那么这个直角三角形的斜边长为__________cm,斜边上的高为_______cm.
3.如图所示,有两棵树,一棵高12米,另一棵高6米,两树相距8米,一只鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行_______米.10104.8据说古埃及人用下图的方法画直角:把一根长绳打上等距离的13个结,然后以3个结、4个结、5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.你知道为什么吗? 用圆规和刻度尺作以下三个直角三角形.使它们的两条直角边分别为3cm,4cm;6cm,8cm;5cm,12cm.然后用刻度尺量出它们斜边的长. 我们发现,它们的斜边长分别为5cm,10cm和13cm. 你能从3cm,4cm,5cm;6cm,8cm,10cm;5cm,12cm, 13cm这三组数据中发现什么规律吗?我们看到:
32+42=52,62+82=102,52+122=132.由此可以猜想出:
在直角三角形中,斜边的平方等于两条直角边的平方和. 以上规律很早就被我国古代劳动人民发现了,他们把直角三角形较短的直角边叫做勾,较长的直角边叫做股,斜边叫做弦.勾股定理:在直角三角形中,两直角边的平方和等于斜边的平方.如图,在△ABC中,∠C=90°,那么
a2+b2=c2.勾股弦你会证明这个定理吗? 先作四个全等的直角三角形,设它们的两直角边长分别为a,b,斜边长为c.然后照图的样子将它们拼成正方形.可以得到(a+b)2=4× ab+c2.
∴a2+2ab+b2=2ab+c2.
∴a2+b2=c2.例1、如图,一颗大树被大风刮到,折断的一段恰好落在地面上的A处,量得BC=5cm,AC=10cm.试计算这颗大树的高度(结果精确到1m).解:在直角三角形ABC中,
∵∠ACB=90°,
∴BC2+AC2=AB2(勾股定理).
∴AB2=52+102=125.
∴AB≈11(m).
树高=AB+BC≈16(m).
答:这棵树约有16m高.某养殖场有一个长2米、宽1.5米的长方形栅栏,现要在相对角的顶点间加固一条木板(木板的宽度忽略不计),则木板的长度应取_________米.2.5例2、已知:Rt△ABC中,∠C=90°,AB=8,BC= .求AC.解:在Rt△ABC中,
∵ ∠C=90°,
∴BC2+AC2=AB2(勾股定理).
∴AC2=82-( )2=46.
∴AC= .如图,有一个圆柱,它的高等于12cm,底面圆的周长为18cm,在圆柱下底面的A点有一只蚂蚁,它想吃到地面上与A点相对的B点处的食物,沿圆柱侧面爬行的最短路程是多少?(1)在你自己做的圆柱上,尝试从点A到点B沿圆
柱侧面画几条路线,你觉得哪条路线最短?(2)如图,将圆柱侧面剪开展成一个长方形,点
A到点B的最短路线是什么?你画对了吗?(B)(3)蚂蚁从点A出发,想吃到B点上的食物,它沿
圆柱侧面爬行的最短路程是多少?12厘米9厘米AB2=122+92AB=15(厘米)1、放学以后,小红和小颖从学校分手,分别沿着东南方向和西南方向回家,若小红和小颖行走的速度都是40米/分,小红用15分钟到家,小颖用20分钟到家,小红和小颖家的距离为 ( )
A.600米 B.800米 C.1000米 D.不能确定
C2、如图,已知四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13.
求:四边形ABCD的面积.解:连接AC,在Rt△ABC中,
AC2=AB2+BC2=32+42=25,
∴ AC=5.
在△ACD中,∵ AC2+CD2=25+122=169,
而 AB2=132=169,
∴ AC2+CD2=AB2,∴ ∠ACD=90°.
故S四边形ABCD=S△ABC+S△ACD 3.有一个高为1.5米,半径是1米的圆柱形油桶,在靠近边的地方有一小孔,从孔中插入一铁棒,已知铁棒在油桶外的部分为0.5米,问这根铁棒有多长?解:设伸入油桶中的长度为 x 米,则最长时:x2=1.52+22,x=2.5.
∴最长是2.5+0.5=3(米)
最短时:x=1.5.
∴最短是1.5+0.5=2(米)
答:这根铁棒的长应在2~3米之间.1、勾股定理:
直角三角形两直角边的平方和等于斜边的平方.
2、 “勾股定理”的应用:
已知直角三角形两边,求第三边.
3.在寻求最短路径时,往往把空间问题平面化,利用勾股定理及其逆定理解决实际问题.转化
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
