第一章第三节 正方形的性质(第1课时) 梯度训练题(含答案)
文档属性
| 名称 | 第一章第三节 正方形的性质(第1课时) 梯度训练题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-14 14:33:32 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
正方形的定义与性质
【基础题】
1.(2017 阳谷县二模)矩形、菱形、正方形都一定具有的性质是( )
A.邻边相等 B.四个角都是直角
C.对角线相等 D.对角线互相平分
2.(2017 渭滨区一模)如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
3.(2017春 南召县期末)如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
4.(2017春 寿光市期中)如图,正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线交正方形ABCD的一边CD于点P,∠FPC的度数是( )
A.135° B.120° C.112.5° D.67.5°
5.(2016 毕节市)如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
【中档题】
6.(2016 贵阳模拟)将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
7.(2016 南充模拟)下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )
A.①②③ B.①② C.①③ D.②③
8.(2016 宁阳县模拟)如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是( )
A.45° B.22.5° C.67.5° D.75°
9.(2016 曹县校级模拟)如图,在正方形ABCD中,H是BC延长线上一点,使CE=CH,连接DH,延长BE交DH于G,则下面结论错误的是( )
A.BE=DH B.∠H+∠BEC=90°
C.BG⊥DH D.∠HDC+∠ABE=90°
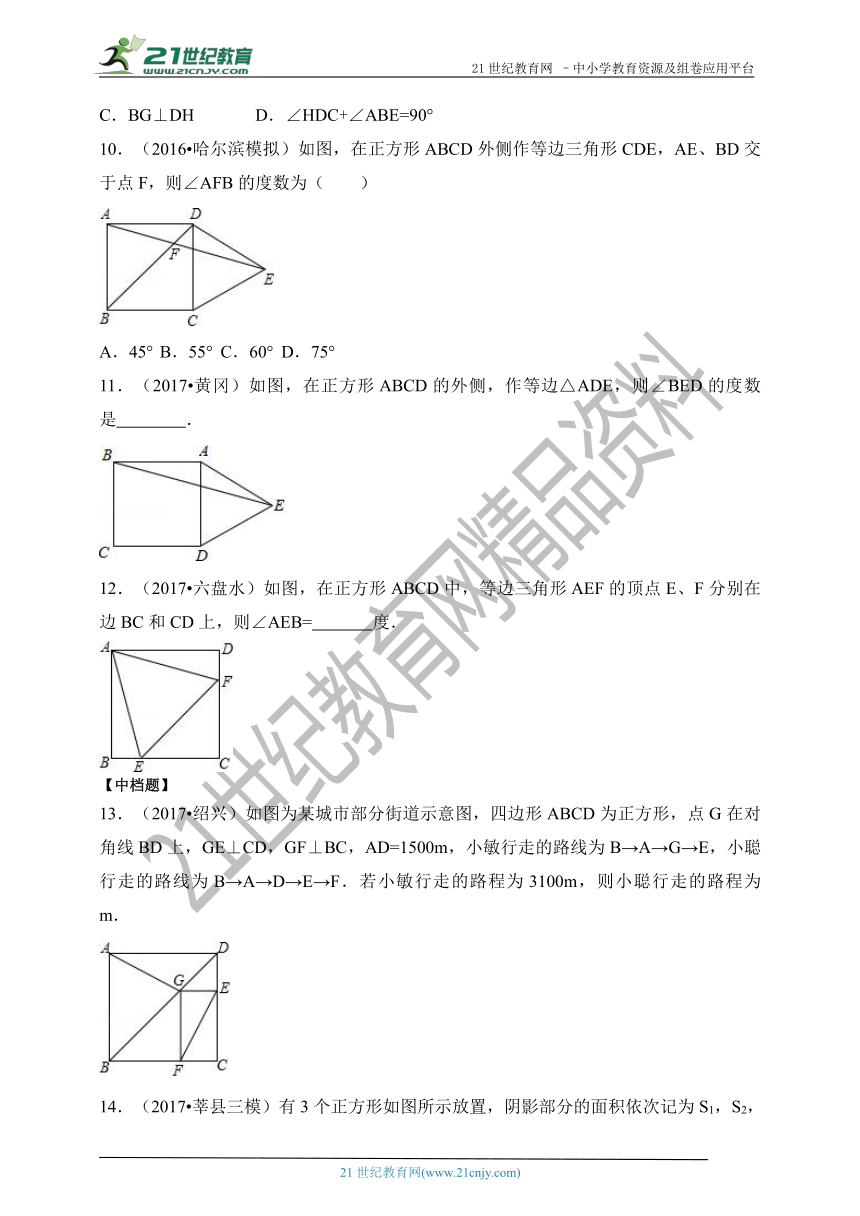
10.(2016 哈尔滨模拟)如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
A.45° B.55° C.60° D.75°
11.(2017 黄冈)如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
12.(2017 六盘水)如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在边BC和CD上,则∠AEB= 度.
【中档题】
13.(2017 绍兴)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
14.(2017 莘县三模)有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2= .
15.(2017 娄底模拟)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是 .
16.(2017 和平区三模)如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6,那么AC= .
【较难题】
17.(2017 陕西)如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.
18.(2017 杭州)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
19.(2017 怀化)如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
20.(2017 番禺区一模)如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.
答案
1.D.2.B.3.D.4.C.5.B6.B.7.B.8.B.9.B.10.C.11.45°.12.75.13.4600
14.4:9.15.5×()403016.16.
17.【解答】证明:∵四边形ABCD是正方形,
∴∠ADF=CDE=90°,AD=CD.
∵AE=CF,
∴DE=DF,
在△ADF和△CDE中,
∴△ADF≌△CDE(SAS),
∴∠DAF=∠DCE,
在△AGE和△CGF中,,
∴△AGE≌△CGF(AAS),
∴AG=CG.
18.
【解答】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,MN=x,
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x2+(2x+x)2,
解得x=,
∴BN=,
∴BG=BN÷cos30°=.
19.
【解答】(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=(180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
20.
【解答】证明:∵四边形ABCD是正方形,
∴∠BAQ=∠ADP=90°,AB=DA,
∵DQ=CP,
∴AQ=DP,
在△ABQ和△DAP中,
,
∴△ABQ≌△DAP(SAS),
∴BQ=AP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
正方形的定义与性质
【基础题】
1.(2017 阳谷县二模)矩形、菱形、正方形都一定具有的性质是( )
A.邻边相等 B.四个角都是直角
C.对角线相等 D.对角线互相平分
2.(2017 渭滨区一模)如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
A.30 B.34 C.36 D.40
3.(2017春 南召县期末)如图,已知四边形ABCD是平行四边形,下列结论中不正确的是( )
A.当AB=BC时,四边形ABCD是菱形
B.当AC⊥BD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD时,四边形ABCD是正方形
4.(2017春 寿光市期中)如图,正方形ABCD的对角线BD是菱形BEFD的一边,菱形BEFD的对角线交正方形ABCD的一边CD于点P,∠FPC的度数是( )
A.135° B.120° C.112.5° D.67.5°
5.(2016 毕节市)如图,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是( )
A.3 B.4 C.5 D.6
【中档题】
6.(2016 贵阳模拟)将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
7.(2016 南充模拟)下列四边形:①正方形、②矩形、③菱形,对角线一定相等的是( )
A.①②③ B.①② C.①③ D.②③
8.(2016 宁阳县模拟)如图,已知P是正方形ABCD对角线BD上一点,且BP=BC,则∠ACP度数是( )
A.45° B.22.5° C.67.5° D.75°
9.(2016 曹县校级模拟)如图,在正方形ABCD中,H是BC延长线上一点,使CE=CH,连接DH,延长BE交DH于G,则下面结论错误的是( )
A.BE=DH B.∠H+∠BEC=90°
C.BG⊥DH D.∠HDC+∠ABE=90°
10.(2016 哈尔滨模拟)如图,在正方形ABCD外侧作等边三角形CDE,AE、BD交于点F,则∠AFB的度数为( )
A.45° B.55° C.60° D.75°
11.(2017 黄冈)如图,在正方形ABCD的外侧,作等边△ADE,则∠BED的度数是 .
12.(2017 六盘水)如图,在正方形ABCD中,等边三角形AEF的顶点E、F分别在边BC和CD上,则∠AEB= 度.
【中档题】
13.(2017 绍兴)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为 m.
14.(2017 莘县三模)有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2= .
15.(2017 娄底模拟)在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作第1个正方形A1B1C1C;延长C1B1交x轴于点A2,作第2个正方形A2B2C2C1,…,按这样的规律进行下去,第2016个正方形的面积是 .
16.(2017 和平区三模)如图所示,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6,那么AC= .
【较难题】
17.(2017 陕西)如图,在正方形ABCD中,E、F分别为边AD和CD上的点,且AE=CF,连接AF、CE交于点G.求证:AG=CG.
18.(2017 杭州)如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
19.(2017 怀化)如图,四边形ABCD是正方形,△EBC是等边三角形.
(1)求证:△ABE≌△DCE;
(2)求∠AED的度数.
20.(2017 番禺区一模)如图,正方形ABCD中,点P,Q分别为AD,CD边上的点,且DQ=CP,连接BQ,AP.求证:BQ=AP.
答案
1.D.2.B.3.D.4.C.5.B6.B.7.B.8.B.9.B.10.C.11.45°.12.75.13.4600
14.4:9.15.5×()403016.16.
17.【解答】证明:∵四边形ABCD是正方形,
∴∠ADF=CDE=90°,AD=CD.
∵AE=CF,
∴DE=DF,
在△ADF和△CDE中,
∴△ADF≌△CDE(SAS),
∴∠DAF=∠DCE,
在△AGE和△CGF中,,
∴△AGE≌△CGF(AAS),
∴AG=CG.
18.
【解答】解:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,MN=x,
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x2+(2x+x)2,
解得x=,
∴BN=,
∴BG=BN÷cos30°=.
19.
【解答】(1)证明:∵四边形ABCD是正方形,△ABC是等边三角形,
∴BA=BC=CD=BE=CE,∠ABC=∠BCD=90°,∠EBC=∠ECB=60°,
∴∠ABE=∠ECD=30°,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS).
(2)∵BA=BE,∠ABE=30°,
∴∠BAE=(180°﹣30°)=75°,
∵∠BAD=90°,
∴∠EAD=90°﹣75°=15°,同理可得∠ADE=15°,
∴∠AED=180°﹣15°﹣15°=150°.
20.
【解答】证明:∵四边形ABCD是正方形,
∴∠BAQ=∠ADP=90°,AB=DA,
∵DQ=CP,
∴AQ=DP,
在△ABQ和△DAP中,
,
∴△ABQ≌△DAP(SAS),
∴BQ=AP.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
