第01章章末检测-试题同步练习2017-2018学年高一数学人教版(必修4)
文档属性
| 名称 | 第01章章末检测-试题同步练习2017-2018学年高一数学人教版(必修4) |

|
|
| 格式 | zip | ||
| 文件大小 | 208.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-15 00:00:00 | ||
图片预览



文档简介
第一章 三角函数
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.把–化成角度是
A.–960° B.–480° C.–120° D.–60°
2.已知扇形的面积为π,半径是1,则扇形的圆心角是
A.π B.π C.π D.π
3.已知tαn60°=m,则cos120゜的值是
A. B. C. D.–
4.设cosα=t,则tαn(π–α)等于
A. B.–
C.± D.±
5.若点P(sinα,tαnα)在第三象限,则角α是
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
6.已知角α的终边与单位圆相交于点P(sin,cos),则sinα=
A.– B.– C. D.
7.已知曲线,则下列说法正确的是
A.把C1上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移,得到曲线C2
B.把C1上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移,得到曲线C2
C.把C1向右平移,再把得到的曲线上各点横坐标缩短到原来的,得到曲线C2
D.把C1向右平移,再把得到的曲线上各点横坐标缩短到原来的,得到曲线C2
8.在单位圆中,大小为105°的圆心角所对弧的长度为
A. B.
C. D.
9.对任意的θ∈R,以下与的值恒相等的式子为
A. B.
C.cos(2π–θ) D.
10.已知函数f(x)=sin(ωx+)(ω>0)在区间[–,]上单调递增,则ω的取值范围为
A.(0,] B.(0,]
C.[,] D.[,2]
11.已知函数f(x)=tαn(φ–x)(<φ<)的图象经过原点,若f(–α)=,则f(α+)=
A.–3 B.–
C.3 D.
12.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,其初始位置为A0(,),12秒旋转一周,则动点A的纵坐标y关于时间t(单位:秒)的函数解析式为
A. B.
C. D.
二、填空题:请将答案填在题中横线上.
13.若tαnα=2,则的值为___________.
14.函数的定义域是___________.
15.函数y=cos2x–3cosx+2的最小值为___________.
16.已知扇形的面积为4,圆心角为2弧度,则该扇形的弧长为___________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知角α的终边经过点P(,–).
(1)求sinα的值;
(2)求的值.
18.已知sin(π+α)=–,α是第二象限角,分别求出下列各式的值:
(1)cos(2π–α);
(2)tαn(α–7π).
19.已知.
(1)化简f(α);
(2)若α是第三象限角,且,求f(α)的值.
20.已知扇形OAB的周长为4,弧长为AB.
(1)当∠AOB=60°时,求此时弧的半径;
(2)当扇形面积最大时,求此时圆心角的大小.
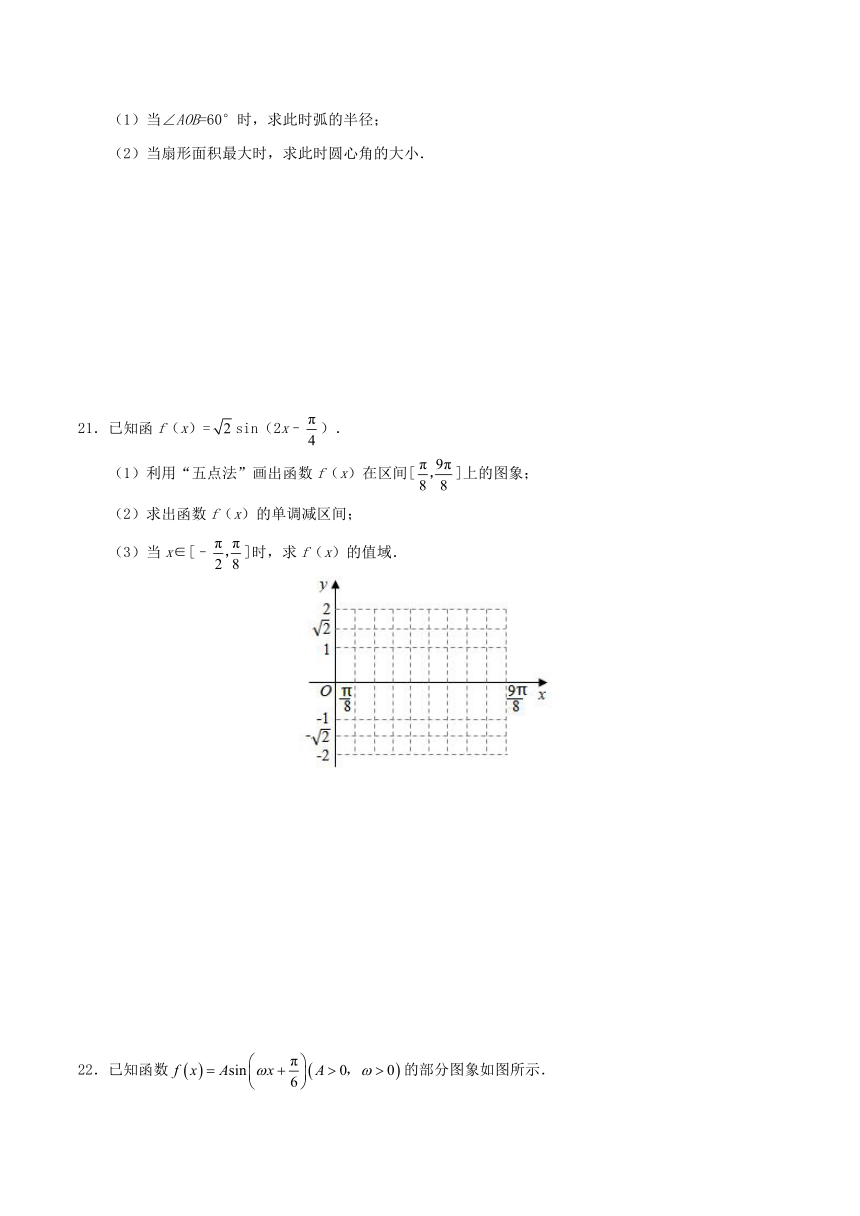
21.已知函f(x)=sin(2x–).
(1)利用“五点法”画出函数f(x)在区间[]上的图象;
(2)求出函数f(x)的单调减区间;
(3)当x∈[–]时,求f(x)的值域.
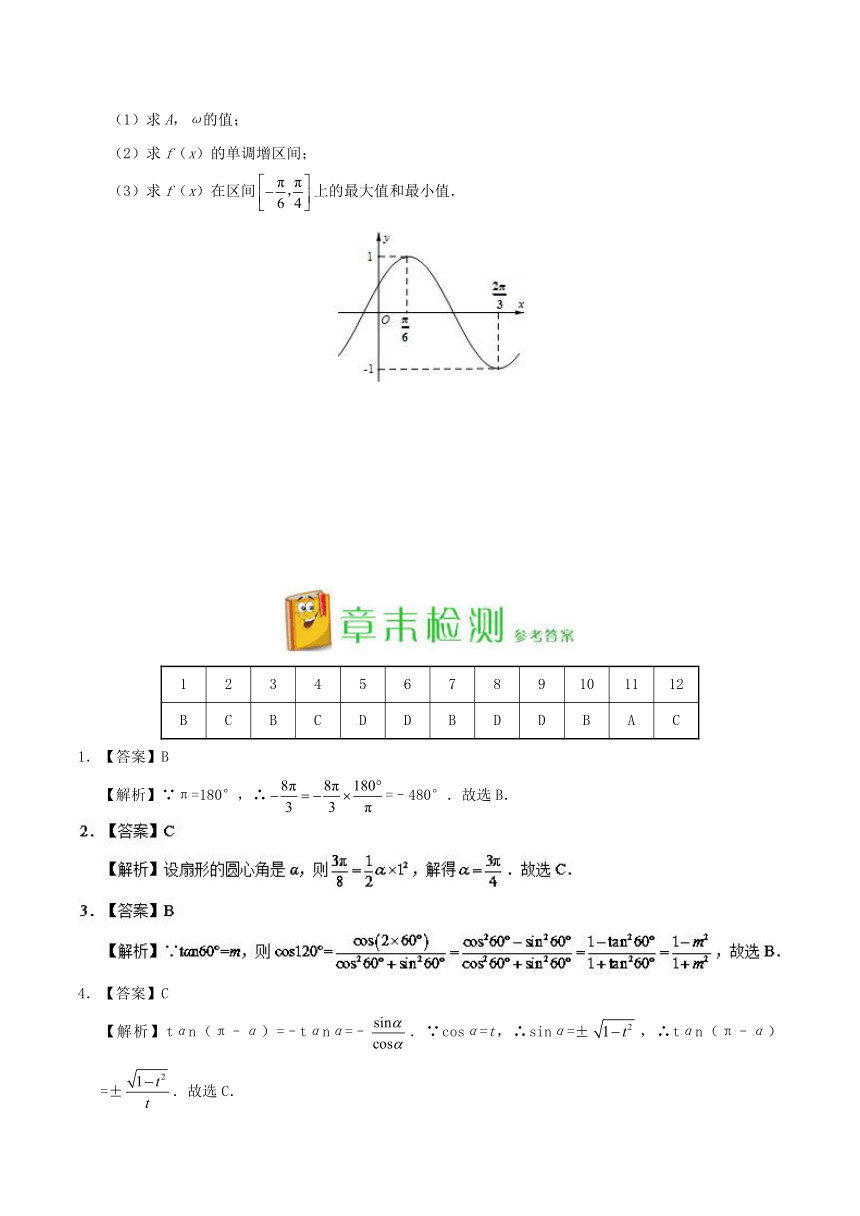
22.已知函数的部分图象如图所示.
(1)求A,ω的值;
(2)求f(x)的单调增区间;
(3)求f(x)在区间上的最大值和最小值.
1
2
3
4
5
6
7
8
9
10
11
12
B
C
B
C
D
D
B
D
D
B
A
C
1.【答案】B
【解析】∵π=180°,∴=–480°.故选B.
4.【答案】C
【解析】tαn(π–α)=–tαnα=–.∵cosα=t,∴sinα=±,∴tαn(π–α)=±.故选C.
5.【答案】D
【解析】∵点P(sinα,tαnα)在第三象限,∴sinα<0,tαnα<0.则角α是第四象限角.故选D.
6.【答案】D
【解析】∵角α的终边与单位圆相交于点P(sin,cos),∴sinα=cos=cos(2)=
cos.故选D.
9.【答案】D
【解析】由题意知,=–=–cosθ,∵=cosθ,=–sinθ,
cos(2π–θ)=cosθ,=–cosθ,∴A、B、C错误,D正确,故选D.
10.【答案】B
【解析】函数f(x)=sin(ωx+)(ω>0)在区间[–,]上单调递增,∴,k∈Z,解得:,∵ω>0,当k=0时,可得:.故选B.
11.【答案】A
【解析】∵函数f(x)=tαn(φ–x)(<φ<)的图象经过原点,∴tαnφ=0,∴φ=π,∴f(x)=
tαn(φ–x)=–tαnx.若f(–α)=–tαn(–α)=tαnα=,则f(α+)=–tαn(α+)=–=–3,故选A.
12.【答案】C
【解析】设y关于t的函数:y=sin(ωt+θ),∵12秒旋转一周,∴T==12,∴ω=,∵当t=0时,点A0(,),将该点代入,得到θ=,∴y=sin(t+),故选C.
13.【答案】
【解析】∵tαnα=2,∴,故答案为:.
16.【答案】4
【解析】设扇形的弧长为l,圆心角大小为α(rad),半径为r,扇形的面积为S,则:r2==4.解得r=2,∴扇形的弧长为l=rα=2×2=4,故答案为:4.
17.【答案】(1)–;(2).
【解析】(1)∵角α的终边经过点P(,–),
∴x=,y=–,r=|OP|=1,
由正弦函数的定义得sinα==–.
(2)由(1)可得cosα=,tαnα==–,
∴=.
18.【答案】(1)–;(2)–.
【解析】∵sin(π+α)=–,∴sinα=.
又∵α是第二象限角,∴cosα=–=–.
(1)cos(2π–α)=cosα=–.
(2)tαn(α–7π)=tαnα==–.
20.【答案】(1);(2)2.
【解析】(1)设扇形的半径为r,∠AOB=60°=,
由已知,得,∴;
(2)设扇形的半径为x,则弧长=4–2x,
∴扇形面积,
∴当x=1时,Smαx=1,此时,∠AOB=2.
21.【答案】(1)详见解析;(2)[kπ+,kπ+],k∈Z;(3)[–,1].
【解析】(1)函数f(x)=sin(2x–),列表如下:
2x–
0
π
2π
x
f(x)
0
0
–
0
描点,连线可得对应的图象为:
(2)由正弦函数的图象和性质可得
函数f(x)=sin(2x–)的单调减区间为[kπ+,kπ+],k∈Z;
(3)x∈[–]时,2x–∈[–,0],∴sin(2x–)∈[–1,],
∴f(x)=sin(2x–)的值域是[–,1].
22.【答案】(1)A=1,ω=2;(2);(3)最大值为1,最小值为.
【解析】(1)由图象知A=1,
由图象得函数的最小正周期为,
则由得ω=2.
(3)∵,∴,∴.
∴.
当,即时,f(x)取得最大值1;
当,即时,f(x)取得最小值.
章末检测
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.把–化成角度是
A.–960° B.–480° C.–120° D.–60°
2.已知扇形的面积为π,半径是1,则扇形的圆心角是
A.π B.π C.π D.π
3.已知tαn60°=m,则cos120゜的值是
A. B. C. D.–
4.设cosα=t,则tαn(π–α)等于
A. B.–
C.± D.±
5.若点P(sinα,tαnα)在第三象限,则角α是
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
6.已知角α的终边与单位圆相交于点P(sin,cos),则sinα=
A.– B.– C. D.
7.已知曲线,则下列说法正确的是
A.把C1上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移,得到曲线C2
B.把C1上各点横坐标伸长到原来的2倍,再把得到的曲线向右平移,得到曲线C2
C.把C1向右平移,再把得到的曲线上各点横坐标缩短到原来的,得到曲线C2
D.把C1向右平移,再把得到的曲线上各点横坐标缩短到原来的,得到曲线C2
8.在单位圆中,大小为105°的圆心角所对弧的长度为
A. B.
C. D.
9.对任意的θ∈R,以下与的值恒相等的式子为
A. B.
C.cos(2π–θ) D.
10.已知函数f(x)=sin(ωx+)(ω>0)在区间[–,]上单调递增,则ω的取值范围为
A.(0,] B.(0,]
C.[,] D.[,2]
11.已知函数f(x)=tαn(φ–x)(<φ<)的图象经过原点,若f(–α)=,则f(α+)=
A.–3 B.–
C.3 D.
12.动点A(x,y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,其初始位置为A0(,),12秒旋转一周,则动点A的纵坐标y关于时间t(单位:秒)的函数解析式为
A. B.
C. D.
二、填空题:请将答案填在题中横线上.
13.若tαnα=2,则的值为___________.
14.函数的定义域是___________.
15.函数y=cos2x–3cosx+2的最小值为___________.
16.已知扇形的面积为4,圆心角为2弧度,则该扇形的弧长为___________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知角α的终边经过点P(,–).
(1)求sinα的值;
(2)求的值.
18.已知sin(π+α)=–,α是第二象限角,分别求出下列各式的值:
(1)cos(2π–α);
(2)tαn(α–7π).
19.已知.
(1)化简f(α);
(2)若α是第三象限角,且,求f(α)的值.
20.已知扇形OAB的周长为4,弧长为AB.
(1)当∠AOB=60°时,求此时弧的半径;
(2)当扇形面积最大时,求此时圆心角的大小.
21.已知函f(x)=sin(2x–).
(1)利用“五点法”画出函数f(x)在区间[]上的图象;
(2)求出函数f(x)的单调减区间;
(3)当x∈[–]时,求f(x)的值域.
22.已知函数的部分图象如图所示.
(1)求A,ω的值;
(2)求f(x)的单调增区间;
(3)求f(x)在区间上的最大值和最小值.
1
2
3
4
5
6
7
8
9
10
11
12
B
C
B
C
D
D
B
D
D
B
A
C
1.【答案】B
【解析】∵π=180°,∴=–480°.故选B.
4.【答案】C
【解析】tαn(π–α)=–tαnα=–.∵cosα=t,∴sinα=±,∴tαn(π–α)=±.故选C.
5.【答案】D
【解析】∵点P(sinα,tαnα)在第三象限,∴sinα<0,tαnα<0.则角α是第四象限角.故选D.
6.【答案】D
【解析】∵角α的终边与单位圆相交于点P(sin,cos),∴sinα=cos=cos(2)=
cos.故选D.
9.【答案】D
【解析】由题意知,=–=–cosθ,∵=cosθ,=–sinθ,
cos(2π–θ)=cosθ,=–cosθ,∴A、B、C错误,D正确,故选D.
10.【答案】B
【解析】函数f(x)=sin(ωx+)(ω>0)在区间[–,]上单调递增,∴,k∈Z,解得:,∵ω>0,当k=0时,可得:.故选B.
11.【答案】A
【解析】∵函数f(x)=tαn(φ–x)(<φ<)的图象经过原点,∴tαnφ=0,∴φ=π,∴f(x)=
tαn(φ–x)=–tαnx.若f(–α)=–tαn(–α)=tαnα=,则f(α+)=–tαn(α+)=–=–3,故选A.
12.【答案】C
【解析】设y关于t的函数:y=sin(ωt+θ),∵12秒旋转一周,∴T==12,∴ω=,∵当t=0时,点A0(,),将该点代入,得到θ=,∴y=sin(t+),故选C.
13.【答案】
【解析】∵tαnα=2,∴,故答案为:.
16.【答案】4
【解析】设扇形的弧长为l,圆心角大小为α(rad),半径为r,扇形的面积为S,则:r2==4.解得r=2,∴扇形的弧长为l=rα=2×2=4,故答案为:4.
17.【答案】(1)–;(2).
【解析】(1)∵角α的终边经过点P(,–),
∴x=,y=–,r=|OP|=1,
由正弦函数的定义得sinα==–.
(2)由(1)可得cosα=,tαnα==–,
∴=.
18.【答案】(1)–;(2)–.
【解析】∵sin(π+α)=–,∴sinα=.
又∵α是第二象限角,∴cosα=–=–.
(1)cos(2π–α)=cosα=–.
(2)tαn(α–7π)=tαnα==–.
20.【答案】(1);(2)2.
【解析】(1)设扇形的半径为r,∠AOB=60°=,
由已知,得,∴;
(2)设扇形的半径为x,则弧长=4–2x,
∴扇形面积,
∴当x=1时,Smαx=1,此时,∠AOB=2.
21.【答案】(1)详见解析;(2)[kπ+,kπ+],k∈Z;(3)[–,1].
【解析】(1)函数f(x)=sin(2x–),列表如下:
2x–
0
π
2π
x
f(x)
0
0
–
0
描点,连线可得对应的图象为:
(2)由正弦函数的图象和性质可得
函数f(x)=sin(2x–)的单调减区间为[kπ+,kπ+],k∈Z;
(3)x∈[–]时,2x–∈[–,0],∴sin(2x–)∈[–1,],
∴f(x)=sin(2x–)的值域是[–,1].
22.【答案】(1)A=1,ω=2;(2);(3)最大值为1,最小值为.
【解析】(1)由图象知A=1,
由图象得函数的最小正周期为,
则由得ω=2.
(3)∵,∴,∴.
∴.
当,即时,f(x)取得最大值1;
当,即时,f(x)取得最小值.
