1.1.1菱形的性质 梯度训练题(含答案)
文档属性
| 名称 | 1.1.1菱形的性质 梯度训练题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-15 00:00:00 | ||
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
菱形的性质与判定
第1课时 菱形的性质
基础题
知识点1 菱形的定义
1.如图,在 ABCD中,∵∠1=∠2,∴BC=DC.∴ ABCD是菱形(________________________).(请在括号内填上理由)
2.如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.小聪认为如果AD平分∠BAC,那么四边形AEDF是菱形,小聪的说法____________(填“正确”或“不正确”).
知识点2 菱形的性质
3.(泸州中考)菱形具有而平行四边形不具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
4.(长沙中考)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.1 B. C.2 D.2
5.(黔西南中考)如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
A.10 B. C.6 D.5
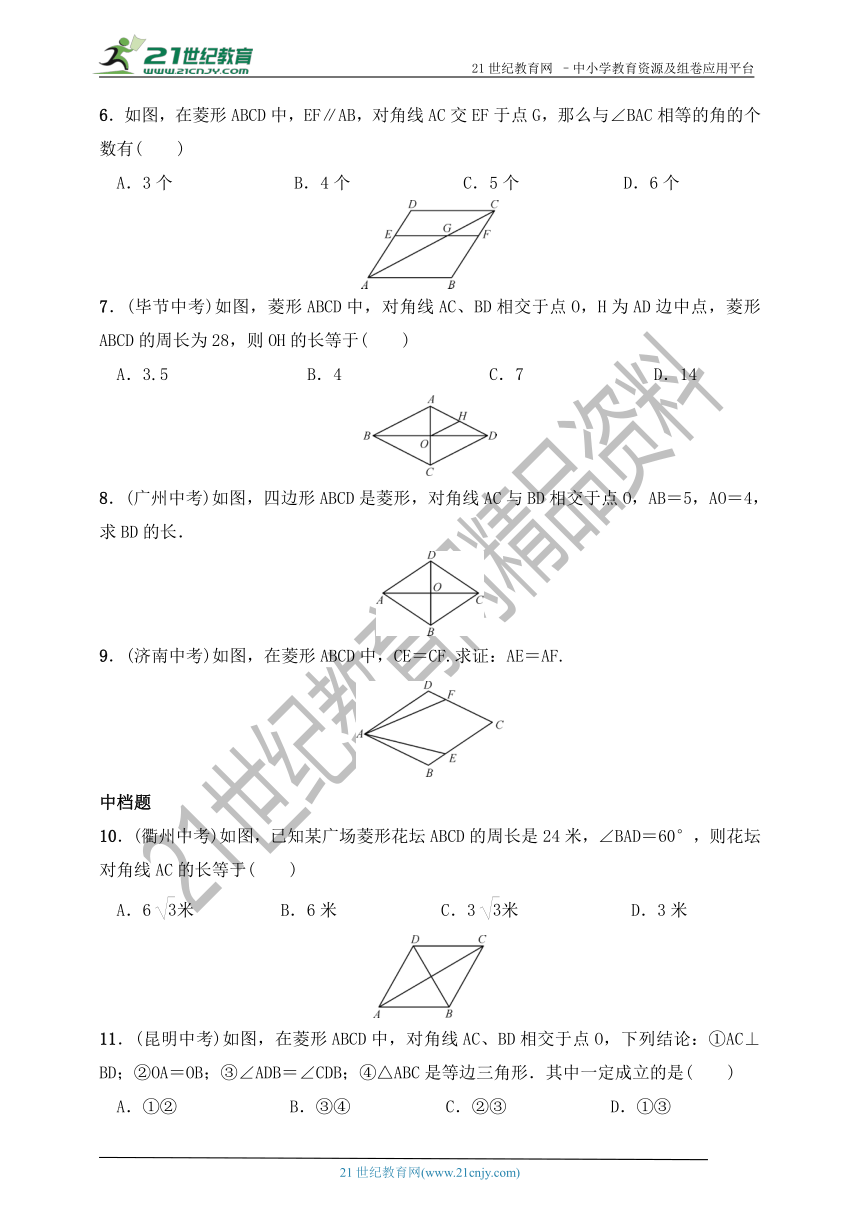
6.如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有( )
A.3个 B.4个 C.5个 D.6个
7.(毕节中考)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )
A.3.5 B.4 C.7 D.14
8.(广州中考)如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AB=5,AO=4,求BD的长.
9.(济南中考)如图,在菱形ABCD中,CE=CF.求证:AE=AF.
中档题
10.(衢州中考)如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
11.(昆明中考)如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形.其中一定成立的是( )
A.①② B.③④ C.②③ D.①③
12.(烟台中考)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
13.(乌鲁木齐中考)若菱形的周长为8,相邻两内角之比为3∶1,则菱形的高是____________.
14.(乐山中考)如图,在△ABC中,AB=AC,四边形ADEF是菱形,求证:BE=CE.
15.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
综合题
16.(贵阳中考)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由
参考答案
1.有一组邻边相等的平行四边形是菱形 2.正确 3.D 4.C 5.D 6.C 7.A
8.∵四边形ABCD是菱形,∴AC⊥BD且BO=DO.在Rt△AOB中,AB=5,AO=4,由勾股定理,得BO=3.∴BD=6.
9.证明:∵四边形ABCD是菱形,∴AD=AB,∠D=∠B,DC=BC.∵CE=CF,∴DC-CF=BC-CE.∴DF=BE.∴△ADF≌△ABE.∴AE=AF.
10.A 11.D 12.C 13.
14.证明:∵四边形ADEF是菱形,∴DE=EF,AB∥EF,DE∥AC.∴∠C=∠BED,∠B=∠CEF.∵AB=AC,∴∠B=∠C.∴∠BED=∠CEF.在△DBE和△FCE中,∴△DBE≌△FCE(AAS).
∴BE=CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
菱形的性质与判定
第1课时 菱形的性质
基础题
知识点1 菱形的定义
1.如图,在 ABCD中,∵∠1=∠2,∴BC=DC.∴ ABCD是菱形(________________________).(请在括号内填上理由)
2.如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.小聪认为如果AD平分∠BAC,那么四边形AEDF是菱形,小聪的说法____________(填“正确”或“不正确”).
知识点2 菱形的性质
3.(泸州中考)菱形具有而平行四边形不具有的性质是( )
A.两组对边分别平行 B.两组对角分别相等
C.对角线互相平分 D.对角线互相垂直
4.(长沙中考)如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线BD的长是( )
A.1 B. C.2 D.2
5.(黔西南中考)如图,在菱形ABCD中,AC与BD相交于点O,AC=8,BD=6,则菱形的边长AB等于( )
A.10 B. C.6 D.5
6.如图,在菱形ABCD中,EF∥AB,对角线AC交EF于点G,那么与∠BAC相等的角的个数有( )
A.3个 B.4个 C.5个 D.6个
7.(毕节中考)如图,菱形ABCD中,对角线AC、BD相交于点O,H为AD边中点,菱形ABCD的周长为28,则OH的长等于( )
A.3.5 B.4 C.7 D.14
8.(广州中考)如图,四边形ABCD是菱形,对角线AC与BD相交于点O,AB=5,AO=4,求BD的长.
9.(济南中考)如图,在菱形ABCD中,CE=CF.求证:AE=AF.
中档题
10.(衢州中考)如图,已知某广场菱形花坛ABCD的周长是24米,∠BAD=60°,则花坛对角线AC的长等于( )
A.6米 B.6米 C.3米 D.3米
11.(昆明中考)如图,在菱形ABCD中,对角线AC、BD相交于点O,下列结论:①AC⊥BD;②OA=OB;③∠ADB=∠CDB;④△ABC是等边三角形.其中一定成立的是( )
A.①② B.③④ C.②③ D.①③
12.(烟台中考)如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO,若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
13.(乌鲁木齐中考)若菱形的周长为8,相邻两内角之比为3∶1,则菱形的高是____________.
14.(乐山中考)如图,在△ABC中,AB=AC,四边形ADEF是菱形,求证:BE=CE.
15.如图,已知菱形ABCD的对角线相交于点O,延长AB至点E,使BE=AB,连接CE.
(1)求证:BD=EC;
(2)若∠E=50°,求∠BAO的大小.
综合题
16.(贵阳中考)已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.
(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由
参考答案
1.有一组邻边相等的平行四边形是菱形 2.正确 3.D 4.C 5.D 6.C 7.A
8.∵四边形ABCD是菱形,∴AC⊥BD且BO=DO.在Rt△AOB中,AB=5,AO=4,由勾股定理,得BO=3.∴BD=6.
9.证明:∵四边形ABCD是菱形,∴AD=AB,∠D=∠B,DC=BC.∵CE=CF,∴DC-CF=BC-CE.∴DF=BE.∴△ADF≌△ABE.∴AE=AF.
10.A 11.D 12.C 13.
14.证明:∵四边形ADEF是菱形,∴DE=EF,AB∥EF,DE∥AC.∴∠C=∠BED,∠B=∠CEF.∵AB=AC,∴∠B=∠C.∴∠BED=∠CEF.在△DBE和△FCE中,∴△DBE≌△FCE(AAS).
∴BE=CE.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
