苏科版八年级数学下册反比例函数专题复习课件 (3课时,共70张PPT)
文档属性
| 名称 | 苏科版八年级数学下册反比例函数专题复习课件 (3课时,共70张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-19 17:31:09 | ||
图片预览











文档简介
课件70张PPT。反比例函数专题复习课件 函数关系式
具有什么共同特征?
课堂探究 具有 的形
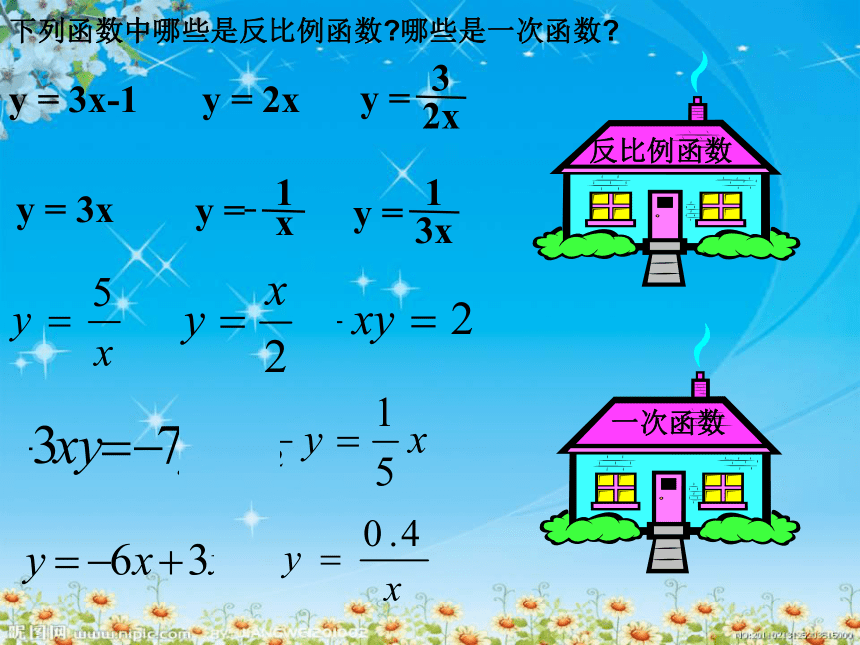
式,其中k≠0,k为常数反比例函数中自变量x的取值范围是什么?不等于o的一切实数。等价形式:(k ≠0)y=kx-1xy=ky与x成反比例例1 下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?可以改写成 ,所以y是x的反比例函数,比例系数k=1。不具备 的形式,所以y不是x的反比例函数。y是x的反比例函数,比例系数k=4。不具备 的形式,所以y不是x的反比例函数。可以改写成 所以y是x的
反比例函数,比例系数k= y = 3x-1y = 2xy = 3x下列函数中哪些是反比例函数?哪些是一次函数? 1. 在下列函数中,y是x的反比例函数的是( )
(A) (B) + 7
(C)xy = 5 (D)
2.已知函数 是正比例函数,则 m=___ ;
已知函数 是反比例函数,则 m = ___ 。C86
关系式xy+4=0中y是x的反比例函数吗?若是,比例系数k等于多少?若不是,请说明理由。xy+4=0可以改写成 比例系数k等于-4所以y是x的反比例函数例1、已知y是x的反比例函数,当x=2时,y=6.
写出y与x的函数关系式:
求当x=4时y的值.因为当 x=2 时y=6,所以有∵y与x的函数关系式为⑵ 把 x=4 代入 得 待定系数法求函数的解析式(1).写出这个反比例函数的表达式;解:∵ y是x的反比例函数,(2).根据函数表达式完成上表.2-41例2:已知y=y1-2y2,y1与x成反比例,y2与x2成正比例,且当x=-1时,y=-5,当x=1时,y=1,求y与x的函数关系式.
及时巩固 将下列各题中y与x的函数关系写出来.
(1)y与x成反比例;
(2)y与z成反比例,z与3x成反比例;
(3)y与2z成反比例,z与X成正比例; 【课堂练习】1.y是x2成反比例,当x=3时,y=4.
(1)写出y与x的函数关系式.
(2)求当y=1.5时x的值.2.已知函y=m+n,其中m与x成正比例,
n与x成反比例,且当x=1时,y=4;
x=2时y=5.
(1)求y与x的函数关系式.
(2)当x=4时,求y的值.当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:{m2-2=-1m+1≠0{即 m=±1m≠-114 .近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式是___________。6、一水池内有污水20 米3,设放完全池污水的时间为t(分钟),每分钟的放水量为w(米3),规定放水时间在4分钟至8分钟之间,请把t表示为w的函数,并给出w的取值范围。
解:由题意知由 x=1 时,y=4由 x=-1 时,y=0反比例函数的图 象 和 性 质 问题:你还记得正比例函数y=kx (k≠0)的图象是什么样子吗?怎样得出来的?它的性质又是什么呢?正比例函数图象是一条过原点直线,通过描点法得来的。活动一动脑思考正比例
y=kx
(k≠0)k>0活动二 分析:所要画的图象是反比例函数的图象,自变量的取值范围是x≠0,怎样取值比较恰当呢?动手画一画1、自变量x需要取多少值?为什么?
2、取值时要注意什么?1、在不知道图象的走向的情况下,取点越多越能反映图象的实际情况,但一般取8—12个值为宜应注意:
1、自变量x≠0;
2、自变量x的取值要对称
3、自变量x的取值要便于计算和描点123456-1-2-3-4-5-6函数图象画法:描点法
1、列表;
2、描点;
3、连线。描点并连线:12345-1-3-2-4-51234-1-2-3-40-6-556xy你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
连线时,一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……画一画
一起看一看活动二动手画一画请模拟例2,在平面直角坐标系中画出反比例函数 与 的函数图像。
活动三仔细看一看 认真想一想 仔细看看教材例2这两个函数图象在同一坐标系内的位置,想想它们之间有什么对称关系?活动三动手画一画活动三看一看 想一想 议一议k=6k=3k=-6k=-31、每个函数的图象是什么形状,有几支?函数有两条曲线,称为双曲线,有两个分支。活动三看一看 想一想 议一议k=6k=3k=-6k=-3k>0k<0 2、每个函数的图象所在的象限与k有什么关系?当k>0时,图象在第一、三象限,
当k<0时,图象在第二、四象限。活动三看一看 想一想 议一议k=6k=3k=-6k=-3k>0k<03、在每一个象限内,y的值随x的值怎样变化?与k有何关系?当k>0时,在每一个象限内,y随x的增大而减小;
当k<0时,在每一个象限内,y随x 的增大而增大。活动三看一看 想一想 议一议k=6k=3k=-6k=-3k>0k<04、它们的图象会与坐标轴相交吗?为什么? 反比例函数的图象可无限接近两坐标轴,但永远不会与坐标轴相交。反比例函数
是不是由k决
定其性质呢?( x≠0, y≠0 )
活动四知识归纳y=kx ( k≠0 )直线双曲线一、三象限一、三象限y随x的增大而增大每个象限内,y随x的增大而减小每个象限内,y随x的增大而增大。y随x的增大而减小二、四象限二、四象限注意:1、双曲线越来越接近两坐标轴,但永远不会与坐标轴相交。活动四火炼真金活动四火炼真金 ( )C活动四火炼真金3. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )D活动四PK中考B解得: k=12∴这个反比例函数的表达式为∵k>0∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。∵图象过点A(2,6)练习:-1AB解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。∵函数的图象在第一、第三象限∴ m-5>0解得 m>5 (2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,∴当a>a′时b<b′变式练习:A(m,n)1思考:=4.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .A.S1>S2
B.S1C.S1 = S2
D.S1和S2的大小关系不能确定. CAA.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S1S3S2求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。1、进一步巩固复习了作函数图象的一般方法和步骤2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。m<23、下列反比例函数图像的一个分支,在第三象限的是( )二、四B2、 下列函数中,其图象位于第二、四象限的有 ,
在其图象所在的象限内,y随x的减小而增大的有 。(1),(4)(2),(3)已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.< 4> 4y1> y2A(x1,y1),B(x2,y2)且x1<0<x2y1 >0>y2若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-10反比例函数图象中的面积问题PB⊥y轴于点B,直线PC经过原点。(1)如图1,反比例函数图像上一点A与坐标轴围成的矩形ABOC的面积是8 ,则该反比例函数的解析式为 .图1xyOCBA(2)如图2,P1、P2、P3是双曲线上的三点.过这三点分别作y轴的垂线,得到三个三角形P1A10、P2A20、P3A30,设它们的面积分别是S1、S2、S3,则( ).
A.S1C.S1(4)如图4,矩形OABC的两边在坐标轴上,且与反比例函数的图像交于点E、F,其中点E、,则k的值 .F分别是BC、AB的中点,若四边形OFBE的面积例MN如图,直线AB过点A(m, 0)、B(0, n)(其中
m>0, n>0).反比例函数 (p>0)的图象与直线AB交于C、D两点,连结OC、OD.
(1)已知m+n=10,△AOB的面积为S,
问:当n何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC、
△COD、△DOB的面积都相等
时,求p的值。作业再见
具有什么共同特征?
课堂探究 具有 的形
式,其中k≠0,k为常数反比例函数中自变量x的取值范围是什么?不等于o的一切实数。等价形式:(k ≠0)y=kx-1xy=ky与x成反比例例1 下列关系式中的y是x的反比例函数吗?如果是,比例系数k是多少?可以改写成 ,所以y是x的反比例函数,比例系数k=1。不具备 的形式,所以y不是x的反比例函数。y是x的反比例函数,比例系数k=4。不具备 的形式,所以y不是x的反比例函数。可以改写成 所以y是x的
反比例函数,比例系数k= y = 3x-1y = 2xy = 3x下列函数中哪些是反比例函数?哪些是一次函数? 1. 在下列函数中,y是x的反比例函数的是( )
(A) (B) + 7
(C)xy = 5 (D)
2.已知函数 是正比例函数,则 m=___ ;
已知函数 是反比例函数,则 m = ___ 。C86
关系式xy+4=0中y是x的反比例函数吗?若是,比例系数k等于多少?若不是,请说明理由。xy+4=0可以改写成 比例系数k等于-4所以y是x的反比例函数例1、已知y是x的反比例函数,当x=2时,y=6.
写出y与x的函数关系式:
求当x=4时y的值.因为当 x=2 时y=6,所以有∵y与x的函数关系式为⑵ 把 x=4 代入 得 待定系数法求函数的解析式(1).写出这个反比例函数的表达式;解:∵ y是x的反比例函数,(2).根据函数表达式完成上表.2-41例2:已知y=y1-2y2,y1与x成反比例,y2与x2成正比例,且当x=-1时,y=-5,当x=1时,y=1,求y与x的函数关系式.
及时巩固 将下列各题中y与x的函数关系写出来.
(1)y与x成反比例;
(2)y与z成反比例,z与3x成反比例;
(3)y与2z成反比例,z与X成正比例; 【课堂练习】1.y是x2成反比例,当x=3时,y=4.
(1)写出y与x的函数关系式.
(2)求当y=1.5时x的值.2.已知函y=m+n,其中m与x成正比例,
n与x成反比例,且当x=1时,y=4;
x=2时y=5.
(1)求y与x的函数关系式.
(2)当x=4时,求y的值.当m= 时,关于x的函数
y=(m+1)xm2-2是反比例函数?
分析:{m2-2=-1m+1≠0{即 m=±1m≠-114 .近视眼镜的度数y(度)与镜片焦距x(米)成反比例,已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数y与镜片焦距x之间的函数关系式是___________。6、一水池内有污水20 米3,设放完全池污水的时间为t(分钟),每分钟的放水量为w(米3),规定放水时间在4分钟至8分钟之间,请把t表示为w的函数,并给出w的取值范围。
解:由题意知由 x=1 时,y=4由 x=-1 时,y=0反比例函数的图 象 和 性 质 问题:你还记得正比例函数y=kx (k≠0)的图象是什么样子吗?怎样得出来的?它的性质又是什么呢?正比例函数图象是一条过原点直线,通过描点法得来的。活动一动脑思考正比例
y=kx
(k≠0)k>0活动二 分析:所要画的图象是反比例函数的图象,自变量的取值范围是x≠0,怎样取值比较恰当呢?动手画一画1、自变量x需要取多少值?为什么?
2、取值时要注意什么?1、在不知道图象的走向的情况下,取点越多越能反映图象的实际情况,但一般取8—12个值为宜应注意:
1、自变量x≠0;
2、自变量x的取值要对称
3、自变量x的取值要便于计算和描点123456-1-2-3-4-5-6函数图象画法:描点法
1、列表;
2、描点;
3、连线。描点并连线:12345-1-3-2-4-51234-1-2-3-40-6-556xy你认为作反比例函数图象时应注意哪些问题?列表时,自变量的值可以选取一些互为相反数的值,这样既可简化计算,又便于对称性描点;
列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便连线,又较准确地表达函数的变化趋势;
连线时,一定要养成按自变量从小到大的顺序,依次用平滑的曲线连接,从中体会函数的增减性;
……画一画
一起看一看活动二动手画一画请模拟例2,在平面直角坐标系中画出反比例函数 与 的函数图像。
活动三仔细看一看 认真想一想 仔细看看教材例2这两个函数图象在同一坐标系内的位置,想想它们之间有什么对称关系?活动三动手画一画活动三看一看 想一想 议一议k=6k=3k=-6k=-31、每个函数的图象是什么形状,有几支?函数有两条曲线,称为双曲线,有两个分支。活动三看一看 想一想 议一议k=6k=3k=-6k=-3k>0k<0 2、每个函数的图象所在的象限与k有什么关系?当k>0时,图象在第一、三象限,
当k<0时,图象在第二、四象限。活动三看一看 想一想 议一议k=6k=3k=-6k=-3k>0k<03、在每一个象限内,y的值随x的值怎样变化?与k有何关系?当k>0时,在每一个象限内,y随x的增大而减小;
当k<0时,在每一个象限内,y随x 的增大而增大。活动三看一看 想一想 议一议k=6k=3k=-6k=-3k>0k<04、它们的图象会与坐标轴相交吗?为什么? 反比例函数的图象可无限接近两坐标轴,但永远不会与坐标轴相交。反比例函数
是不是由k决
定其性质呢?( x≠0, y≠0 )
活动四知识归纳y=kx ( k≠0 )直线双曲线一、三象限一、三象限y随x的增大而增大每个象限内,y随x的增大而减小每个象限内,y随x的增大而增大。y随x的增大而减小二、四象限二、四象限注意:1、双曲线越来越接近两坐标轴,但永远不会与坐标轴相交。活动四火炼真金活动四火炼真金 ( )C活动四火炼真金3. 已知k<0,则函数 y1=kx,y2= 在同一坐标系中的图象大致是 ( )D活动四PK中考B解得: k=12∴这个反比例函数的表达式为∵k>0∴这个函数的图象在第一、第三象限,
在每个象限内,y随x的增大而减小。∵图象过点A(2,6)练习:-1AB解:(1)反比例函数图象的分布只有两种可能,分布在第一、第三象限,或者分布在第二、第四象限。这个函数的图象的一支在第一象限,则另一支必在第三象限。∵函数的图象在第一、第三象限∴ m-5>0解得 m>5 (2)∵m-5>0,在这个函数图象的任一支上,y随x的增大而减小,∴当a>a′时b<b′变式练习:A(m,n)1思考:=4.如图,点P是反比例函数图象上的一点,过点P分别向x轴、y轴作垂线,若阴影部分面积为3,则这个反比例函数的
关系式是 .A.S1>S2
B.S1
D.S1和S2的大小关系不能确定. CAA.S1 = S2 = S3
B. S1 < S2 < S3
C. S3 < S1 < S2
D. S1 > S2 >S3 S1S3S2求(1)一次函数的解析式
(2)根据图像写出使一 次函数的值小于反比例函数的值的x的取值范围。1、进一步巩固复习了作函数图象的一般方法和步骤2、亲手画出函数的图象,用类比的方法,数形结合的思想,有了对图形进行观察、分析和归纳的体验,掌握了反比例函数的图象和性质当k>0时,双曲线的两支分别位于第一、第三象限, 在每个象限内y值随x值的增大而减小。当k<0时,双曲线的两支分别位于第二、第四象限, 在每个象限内y值随x值的增大而增大。m<23、下列反比例函数图像的一个分支,在第三象限的是( )二、四B2、 下列函数中,其图象位于第二、四象限的有 ,
在其图象所在的象限内,y随x的减小而增大的有 。(1),(4)(2),(3)已知反比例函数
若函数的图象位于第一三象限,
则k_____________;
若在每一象限内,y随x增大而增大,
则k_____________.< 4> 4y1> y2A(x1,y1),B(x2,y2)且x1<0<x2y1 >0>y2若点(-2,y1)、(-1,y2)、(2,y3)在
反比例函数 的图象上,则( )A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-1
A.S1
m>0, n>0).反比例函数 (p>0)的图象与直线AB交于C、D两点,连结OC、OD.
(1)已知m+n=10,△AOB的面积为S,
问:当n何值时,S取最大值?并求这个最大值;
(2)若m=8,n=6,当△AOC、
△COD、△DOB的面积都相等
时,求p的值。作业再见
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
