1.1 菱形的性质与判定(1)同步作业
文档属性
| 名称 | 1.1 菱形的性质与判定(1)同步作业 |  | |
| 格式 | doc | ||
| 文件大小 | 773.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-19 12:19:43 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.1 菱形的性质与判定(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.平行四边形的一条边长是10cm,那么它的两条对角线的长可能是( )
A.6cm和8cm B.10cm和20cm C.8cm和12cm D.12cm和32cm
2.如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )
A. 24 B. 16 C. 4 D. 2
3.菱形的两条对角线长分别为和,则它的周长和面积分别为( )
A. B. C. D.
INCLUDEPICTURE "http://img..net/quiz/images/201112/49/8aabb84a.png" \* MERGEFORMATINET INCLUDEPICTURE "http://img..net/quiz/images/201112/49/8aabb84a.png" \* MERGEFORMATINET
4.如图,在菱形中,,,、分别是边、中点,则周长等于( )
A. B. C. D.
5.如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
A. 5 B. 10 C. 15 D. 20
6.如图,已知菱形ABCD的周长为16,面积为,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A. 2 B. 2 C. 4 D. 4
7.在如图直角坐标系内,四边形AOBC是边长为2的菱形,E为边OB的中点,连结AE与对角线OC交于点D,且∠BCO=∠EAO,则点D坐标为( )
A. (,) B. (1,) C. (,) D. (1,)
8.如图,已知菱形ABCD的边长等于2,若∠DAB=60°,则对角线BD的长为( )
A. 1 B. C. 2 D.
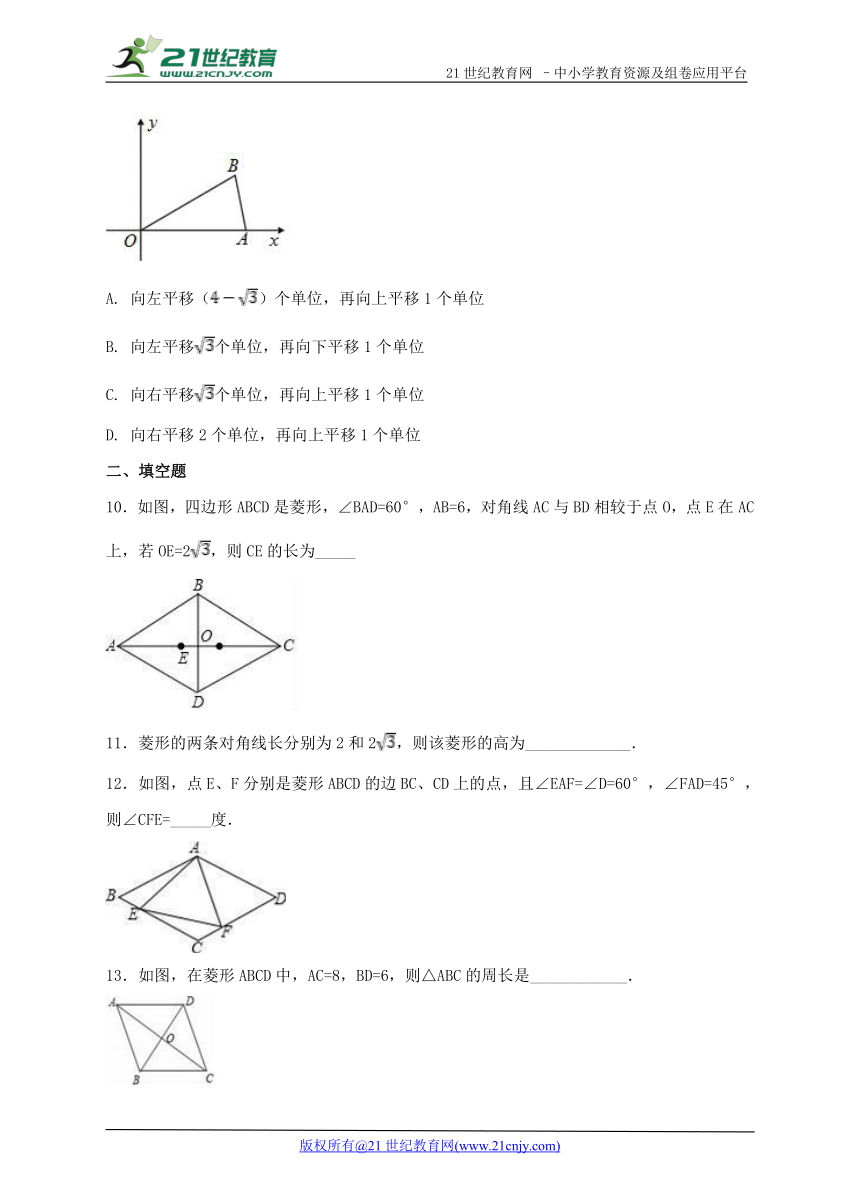
9.如图,在平面直角坐标系中,已知点,若平移点到点,使以点为顶点的四边形是菱形,则正确的平移方法是( )
A. 向左平移()个单位,再向上平移1个单位
B. 向左平移个单位,再向下平移1个单位
C. 向右平移个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
二、填空题
10.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2,则CE的长为_____
11.菱形的两条对角线长分别为2和2,则该菱形的高为_____________.
12.如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_____度.
13.如图,在菱形ABCD中,AC=8,BD=6,则△ABC的周长是____________.
14.菱形ABCD中, ,其周长为32,则菱形面积为____________.
15.如图,菱形ABC的对角线相交于点O,过点D作DE∥AC,且DE= EMBED Equation.DSMT4 AC,连接CE、OE、AE,AE交OD于点F,若AB=2,∠ABC=60°,则AE的长_____.
三、解答题
16.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF.
17.如图,四边形ABCD是边长为2的菱形,E,F分别是AB,AD的中点,连接EF,EC,将△FAE绕点F旋转180°得到△FDM.
(1)补全图形并证明:EF⊥AC;
(2)若∠B=60°,求△EMC的面积.
18.如图,已知E、F分别是 ABCD的边BC、AD上的点,且.
求证:四边形AECF是平行四边形;
若四边形AECF是菱形,且,,求BE的长.
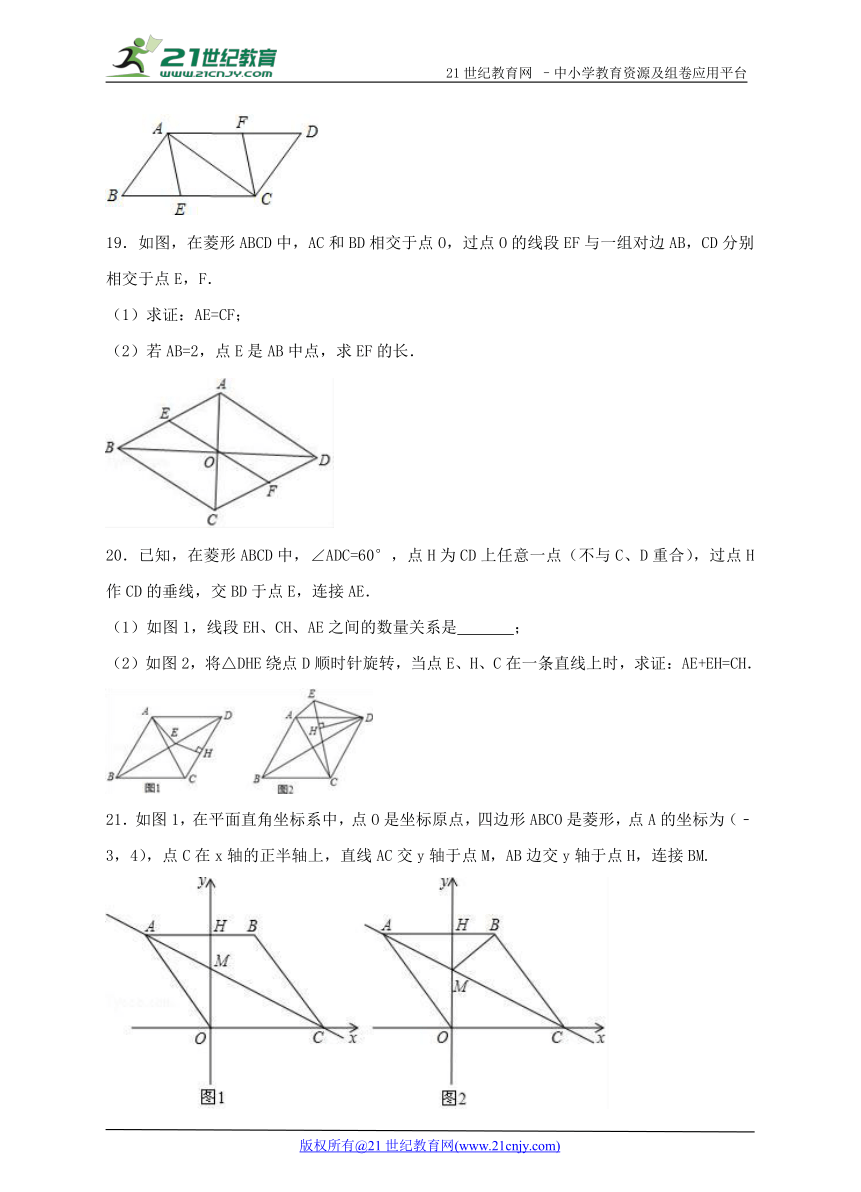
19.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
20.已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
21.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
参考答案
1.B
【解析】解:根据平行四边形的对角线互相平分,所选择作为对角线长度的一半与已知边长需要构成三角形的边长,必须满足三角形的两边之和大于第三边,由此逐一排除;
A、取对角线的一半与已知边长,得3,4,10,不能构成三角形,舍去;
B、取对角线的一半与已知边长,得5,10,10,能构成三角形;
C、取对角线的一半与已知边长,得4,6,10,不能构成三角形,舍去;
D、取对角线的一半与已知边长,得6,16,10,不能构成三角形,舍去.
故选B.
2.C
【解析】【分析】根据菱形的性质可得AO=3,OD=2,AC⊥BD,在Rt△AOD中利用勾股定理求出AD的长,再由菱形的四边相等,即可求得菱形ABCD的周长.
【详解】∵四边形ABCD是菱形,AC=6,BD=4,
∴AO=AC=3,DO=BD=2,AC⊥BD,AB=BC=CD=AD,
在Rt△AOD中,AD=,
∴菱形ABCD的周长为4,
故答案为:4.
【点睛】本题考查了菱形的性质,掌握菱形的对角线互相垂直且平分是解答本题的关键.
3.B
【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD,
∵AC=8cm,BD=6cm,∴AD=5cm,周长=4×5=20 cm, S菱形ABCD=AC BD=24cm2.故选B.
4.B
【解析】分析:分别判断△ABC,△AEF是等边三角形,用勾股定理求出AE的长.
详解:连接AC,因为∠B=60°,BA=BC,所以△ABC是等边三角形,
因为E,F分别是边BC,CD的中点,所以△AEF是等边三角形.
因为AB=2,所以BE=1,由勾股定理得AE=,
所以△AEF的周长为.
故选B.
点睛:在菱形中,如果有60°的内角,则其中一定会有等边三角形,一般结合一边上的高,或对角线互相垂直构造直角三角形,用勾股定理求解.
5.A
【解析】试题解析:∵四边形ABCD是菱形,
∴∠B+∠BCD=180°,AB=BC,
∵∠B:∠BCD=1:2,
∴∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=5.
故选A.
6.B
【解析】试题解析:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB CE′=8,
∴CE′=2,
在Rt△BCE′中,BE′=,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2,
故选:B.
7.D
【解析】分析:首先根据菱形的性质得出△AOD为等腰三角形,根据菱形的性质得出∠BOA=2∠AOE,结合AO=2OE得出△AOD为底角为30°角的等腰三角形,从而得出点D的坐标.
详解:∵BC∥OA, ∴∠BCO=∠COA, 又∵∠BCO=∠EAO, ∴∠COA=∠EAO,
∴△AOD为等腰三角形, ∴点D的横坐标为1, ∵四边形OACB为菱形,
∴∠BOA=2∠AOE, ∵AO=2OE, ∴∠DAO=∠DOA=30°,
∴点D的纵坐标为, ∴点D的坐标为(1,).故选D.
点睛:本题主要考查的是菱形的性质以及等腰三角形的性质,难度中等.理解菱形的性质以及得出△AOD为特殊等腰三角形是解题的关键.
8.C
【解析】试题解析:∵菱形ABCD的边长为2,
∴AD=AB=2,
又∵∠DAB=60°,
∴△DAB是等边三角形,
∴AD=BD=AB=2,
则对角线BD的长是2.
故选C.
9.C
【解析】分析:过点B作BH⊥OA,交OA于点H,利用勾股定理可求出OB的长,进而可得点A向左或向右平移的距离,由菱形的性质可知BC∥OA,所以可得向上或向下平移的距离,问题得解.
详解:过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,
过B作BH⊥x轴于H,
∵B(,1),
∴OB=,
∵A(2,0),
∴C(3,1)
∴OA=OB,
∴则四边形OACB是菱形,
∴平移点A到点C,向右平移个单位,再向上平移1个单位而得到,
故选C.
点睛:本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
10.5或
【解析】分析:由菱形的性质证出△ABD是等边三角形,得出BD=AB=6,由勾股定理得出,即可得出答案.
详解:∵四边形ABCD是菱形,
∴AB=AD=6,AC⊥BD,OB=OD,OA=OC,
∵
∴△ABD是等边三角形,
∴BD=AB=6,
∴
∴
∴
∵点E在AC上,
∴当E在点O左边时
当点E在点O右边时
∴或;
故答案为:或.
点睛:考查菱形的性质,注意分类讨论思想在数学中的应用,不要漏解.
11.
【解析】分析:根据对角线的长度即可计算菱形的面积,根据菱形对角线互相垂直平分的性质,可以求得△AOB为直角三角形,根据AO,BO可以求得AB的值,根据菱形的面积和边长即可解题.
详解:如图,
由题意知AC=2,BD=2,
则菱形的面积S=×2×2=2,
∵菱形对角线互相垂直平分,
∴△AOB为直角三角形,AO=1,BO=,
∴AB= =2,
∴菱形的高h==.
故答案为:.
点睛:本题考查了勾股定理在直角三角形中的运用,菱形面积的计算,本题中求根据AO,BO的值求AB是解题的关键.
12.45
【解析】分析:首先证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,最后可求出∠AFD,∠CFE的度数.
详解:连接AC,
∵菱形ABCD,∴AB=BC,∠B=∠D=60°,
∴△ABC为等边三角形,∠BCD=120°
∴AB=AC,∠ACF=∠BCD=60°,
∴∠B=∠ACF,
∵△ABC为等边三角形,
∴∠BAC=60°,即∠BAE+∠EAC=60°,
又∠EAF=60°,即∠CAF+∠EAC=60°,
∴∠BAE=∠CAF,
在△ABE与△ACF中
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∠EAF=∠D=60°,则△AEF是等边三角形,
∴∠AFE=60°,
又∠AFD=180°-45°-60°=75°,
则∠CFE=180°-75°-60°=45°.
故答案为:45.
点睛:此题主要考查菱形的性质和等边三角形的判定以及三角形的内角和定理.
13.18
【解析】分析:利用菱形的性质结合勾股定理得出AB的长,进而得出答案.
详解:∵在菱形ABCD中,AC=8,BD=6,
∴AB=BC,∠AOB=90°,AO=4,BO=3,
∴BC=AB=,
∴△ABC的周长=AB+BC+AC=5+5+8=18.
故答案为:18
点睛:本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.
14.
【解析】分析:根据菱形的性质易得AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,再判定△ABD为等边三角形,根据等边三角形的性质可得AB=BD=8,从而得OB=4,在Rt△AOB中,根据勾股定理可得OA=4,继而求得AC=2AO=,再由菱形的面积公式即可求得菱形ABCD的面积.
详解:∵菱形ABCD中,其周长为32,
∴AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,
∵,
∴△ABD为等边三角形,
∴AB=BD=8,
∴OB=4,
在Rt△AOB中,OB=4,AB=8,
根据勾股定理可得OA=4,
∴AC=2AO=,
∴菱形ABCD的面积为: =.
点睛:本题考查了菱形性质:1.菱形的四个边都相等;2.菱形对角线相互垂直平分,并且每一组对角线平分一组对角;3.菱形面积公式=对角线乘积的一半.
15.
【解析】在菱形ABCD中,OC=AC,AC⊥BD,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴平行四边形OCED是矩形,
∵在菱形ABCD中,∠ABC=60°,
∴△ABC为等边三角形,
∴AD=AB=AC=2,OA=AC=1,
在矩形OCED中,由勾股定理得:CE=OD===,
在Rt△ACE中,由勾股定理得:AE===;
故答案是:.
16.见解析
【解析】分析:先利用菱形的性质得出∠A=∠C,AD=CD,再结合已知条件中的垂直条件,又可得∠AED=∠CFD,从而利用AAS可证两个三角形全等.
详解:
证明:∵四边形ABCD是菱形,
∴∠A=∠C,AD=CD,
又∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS).
点睛:本题考查了菱形的性质,全等三角形的判定,解题的关键是根据菱形的性质得出两三角形全等的条件.
17.(1)证明见解析;(2).
【解析】分析:
(1)①按要求画出图形即可;②连接BD,由已知条件可知EF是△ABD的中位线,由此可得EF∥BD,由菱形的性质可得AC⊥BD,从而可得EF⊥AC;
(2)由已知条件易得△ABC是等边三角形,结合点E是AB的中点可得CE⊥AB,结合AB∥CD可得CE⊥MC,在Rt△BCE中由已知条件求得CE的长,由已知易得AE=1,由此可得MD=1,从而可得CD的长,这样即可由S△CME=MC·CE求出其面积了.
详解:
(1)①补全图形如下图所示:
②如下图,连接DB,
∵四边形ABCD是菱形,
∴DB⊥AC,
∵E,F分别是AB,AD的中点,
∴EF∥BD.
∴EF⊥AC.
(2)∵四边形ABCD是菱形,
∴AB=BC.
∵∠B=60°,
∴△ABC是等边三角形,
∵E是AB的中点,
∴CE⊥AB,CE⊥MC.
即△EMC是直角三角形,且CE=BC×sin60°=.
由(1)得MD=AE=AB=1.
∴MC=MD+DC=3.
∴S△EMC=MC×CE=.
点睛:(1)解第1小题时,连接BD,证得EF是三角形ABD的中位线得到EF∥BD是解答本问的关键;(2)解第2小题时,证得△ABC是等边三角形,结合点E是AB边的中点得到CE⊥AB,从而得到CE⊥MC是解题的关键.
18.(1)见解析;(2)5
【解析】分析:(1)利用平行四边形的性质得出AF∥EC,进而得出AF=EC,进而求出即可;
(2)利用菱形的性质以及三角形内角和定理得出∠1=∠2,进而求出∠3=∠4,再利用直角三角形的性质得出答案.
详解:证明:四边形ABCD是平行四边形,
,且,
,
,
,
四边形AECF是平行四边形.
解:四边形AECF是菱形,
,
,
,
,,
,
,
.
点睛:此题主要考查了平行四边形的性质与判定,平行线的性质,菱形的性质,直角三角形的性质,等腰三角形的判定,得出∠3=∠4是解答本题的关键.
19.(1)见解析;(2)2
【解析】分析:(1)由四边形ABCD是菱形,可得AB∥CD,OA=OC,继而证得△AOE≌△COF,则可证得结论.
(2)利用平行四边形的判定和性质解答即可.
详解:(1)∵四边形ABCD是菱形,
∴AO=CO,AB∥CD,
∴∠EAO=∠FCO,∠AEO=∠CFO.
在△OAE和△OCF中,
∠EAO=∠FCO,AO=CO,∠AEO=∠CFO,
∴△AOE≌△COF,
∴AE=CF;
(2)∵E是AB中点,
∴BE=AE=CF.
∵BE∥CF,
∴四边形BEFC是平行四边形,
∵AB=2,
∴EF=BC=AB=2.
点睛:此题考查了菱形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
20.(1) EH2+CH2=AE2;(2)见解析.
【解析】分析:(1)如图1,过E作EM⊥AD于M,由四边形ABCD是菱形,得到AD=CD,∠ADE=∠CDE,通过△DME≌△DHE,根据全等三角形的性质得到EM=EH,DM=DH,等量代换得到AM=CH,根据勾股定理即可得到结论;
(2)如图2,根据菱形的性质得到∠BDC=∠BDA=30°,DA=DC,在CH上截取HG,使HG=EH,推出△DEG是等边三角形,由等边三角形的性质得到∠EDG=60°,推出△DAE≌△DCG,根据全等三角形的性质即可得到结论.
详解:
(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG﹣∠ADG=∠ADC﹣∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.
点睛:考查了全等三角形的判定和性质、菱形的性质、旋转的性质、等边三角形的判定和性质,解题的关键是正确的作出辅助线.
21.(1)5;(2)直线AC的解析式y=﹣x+;(3)见解析.
【解析】分析:(1)Rt△AOH中利用勾股定理即可求得菱形的边长;
(2)根据(1)即可求的OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式;
(3)根据S△ABC=S△AMB+S△BMC求得M到直线BC的距离为h,然后分成P在AM上和在MC上两种情况讨论,利用三角形的面积公式求解.
详解:(1)Rt△AOH中,
AO===5,
所以菱形边长为5;
故答案为:5;
(2)∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,得
,解得,
直线AC的解析式y=﹣x+;
(3)设M到直线BC的距离为h,
当x=0时,y=,即M(0,),HM=HO﹣OM=4﹣=,
由S△ABC=S△AMB+SBMC=AB OH=AB HM+BC h,
×5×4=×5×+×5h,解得h=,
①当0<t<时,BP=BA﹣AP=5﹣2t,HM=OH﹣OM=,
S=BP HM=×(5﹣2t)=﹣t+;
②当2.5<t≤5时,BP=2t﹣5,h=,
S=BP h=×(2t﹣5)=t﹣,
把S=3代入①中的函数解析式得,3=﹣t+,
解得:t=,
把S=3代入②的解析式得,3=t﹣,
解得:t=.
∴t=或.
点睛:本题考查了待定系数法求一次函数的解析式以及菱形的性质,根据三角形的面积关系求得M到直线BC的距离h是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
1.1 菱形的性质与判定(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.平行四边形的一条边长是10cm,那么它的两条对角线的长可能是( )
A.6cm和8cm B.10cm和20cm C.8cm和12cm D.12cm和32cm
2.如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )
A. 24 B. 16 C. 4 D. 2
3.菱形的两条对角线长分别为和,则它的周长和面积分别为( )
A. B. C. D.
INCLUDEPICTURE "http://img..net/quiz/images/201112/49/8aabb84a.png" \* MERGEFORMATINET INCLUDEPICTURE "http://img..net/quiz/images/201112/49/8aabb84a.png" \* MERGEFORMATINET
4.如图,在菱形中,,,、分别是边、中点,则周长等于( )
A. B. C. D.
5.如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
A. 5 B. 10 C. 15 D. 20
6.如图,已知菱形ABCD的周长为16,面积为,E为AB的中点,若P为对角线BD上一动点,则EP+AP的最小值为( )
A. 2 B. 2 C. 4 D. 4
7.在如图直角坐标系内,四边形AOBC是边长为2的菱形,E为边OB的中点,连结AE与对角线OC交于点D,且∠BCO=∠EAO,则点D坐标为( )
A. (,) B. (1,) C. (,) D. (1,)
8.如图,已知菱形ABCD的边长等于2,若∠DAB=60°,则对角线BD的长为( )
A. 1 B. C. 2 D.
9.如图,在平面直角坐标系中,已知点,若平移点到点,使以点为顶点的四边形是菱形,则正确的平移方法是( )
A. 向左平移()个单位,再向上平移1个单位
B. 向左平移个单位,再向下平移1个单位
C. 向右平移个单位,再向上平移1个单位
D. 向右平移2个单位,再向上平移1个单位
二、填空题
10.如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2,则CE的长为_____
11.菱形的两条对角线长分别为2和2,则该菱形的高为_____________.
12.如图,点E、F分别是菱形ABCD的边BC、CD上的点,且∠EAF=∠D=60°,∠FAD=45°,则∠CFE=_____度.
13.如图,在菱形ABCD中,AC=8,BD=6,则△ABC的周长是____________.
14.菱形ABCD中, ,其周长为32,则菱形面积为____________.
15.如图,菱形ABC的对角线相交于点O,过点D作DE∥AC,且DE= EMBED Equation.DSMT4 AC,连接CE、OE、AE,AE交OD于点F,若AB=2,∠ABC=60°,则AE的长_____.
三、解答题
16.如图,已知四边形ABCD是菱形,DE⊥AB,DF⊥BC,求证:△ADE≌△CDF.
17.如图,四边形ABCD是边长为2的菱形,E,F分别是AB,AD的中点,连接EF,EC,将△FAE绕点F旋转180°得到△FDM.
(1)补全图形并证明:EF⊥AC;
(2)若∠B=60°,求△EMC的面积.
18.如图,已知E、F分别是 ABCD的边BC、AD上的点,且.
求证:四边形AECF是平行四边形;
若四边形AECF是菱形,且,,求BE的长.
19.如图,在菱形ABCD中,AC和BD相交于点O,过点O的线段EF与一组对边AB,CD分别相交于点E,F.
(1)求证:AE=CF;
(2)若AB=2,点E是AB中点,求EF的长.
20.已知,在菱形ABCD中,∠ADC=60°,点H为CD上任意一点(不与C、D重合),过点H作CD的垂线,交BD于点E,连接AE.
(1)如图1,线段EH、CH、AE之间的数量关系是 ;
(2)如图2,将△DHE绕点D顺时针旋转,当点E、H、C在一条直线上时,求证:AE+EH=CH.
21.如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H,连接BM.
(1)菱形ABCO的边长
(2)求直线AC的解析式;
(3)动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,
①当0<t<时,求S与t之间的函数关系式;
②在点P运动过程中,当S=3,请直接写出t的值.
参考答案
1.B
【解析】解:根据平行四边形的对角线互相平分,所选择作为对角线长度的一半与已知边长需要构成三角形的边长,必须满足三角形的两边之和大于第三边,由此逐一排除;
A、取对角线的一半与已知边长,得3,4,10,不能构成三角形,舍去;
B、取对角线的一半与已知边长,得5,10,10,能构成三角形;
C、取对角线的一半与已知边长,得4,6,10,不能构成三角形,舍去;
D、取对角线的一半与已知边长,得6,16,10,不能构成三角形,舍去.
故选B.
2.C
【解析】【分析】根据菱形的性质可得AO=3,OD=2,AC⊥BD,在Rt△AOD中利用勾股定理求出AD的长,再由菱形的四边相等,即可求得菱形ABCD的周长.
【详解】∵四边形ABCD是菱形,AC=6,BD=4,
∴AO=AC=3,DO=BD=2,AC⊥BD,AB=BC=CD=AD,
在Rt△AOD中,AD=,
∴菱形ABCD的周长为4,
故答案为:4.
【点睛】本题考查了菱形的性质,掌握菱形的对角线互相垂直且平分是解答本题的关键.
3.B
【解析】∵四边形ABCD是菱形,∴AC⊥BD,OA=OC,OB=OD,AB=BC=CD=AD,
∵AC=8cm,BD=6cm,∴AD=5cm,周长=4×5=20 cm, S菱形ABCD=AC BD=24cm2.故选B.
4.B
【解析】分析:分别判断△ABC,△AEF是等边三角形,用勾股定理求出AE的长.
详解:连接AC,因为∠B=60°,BA=BC,所以△ABC是等边三角形,
因为E,F分别是边BC,CD的中点,所以△AEF是等边三角形.
因为AB=2,所以BE=1,由勾股定理得AE=,
所以△AEF的周长为.
故选B.
点睛:在菱形中,如果有60°的内角,则其中一定会有等边三角形,一般结合一边上的高,或对角线互相垂直构造直角三角形,用勾股定理求解.
5.A
【解析】试题解析:∵四边形ABCD是菱形,
∴∠B+∠BCD=180°,AB=BC,
∵∠B:∠BCD=1:2,
∴∠B=60°,
∴△ABC是等边三角形,
∴AB=BC=AC=5.
故选A.
6.B
【解析】试题解析:如图作CE′⊥AB于E′,交BD于P′,连接AC、AP′.
∵已知菱形ABCD的周长为16,面积为8,
∴AB=BC=4,AB CE′=8,
∴CE′=2,
在Rt△BCE′中,BE′=,
∵BE=EA=2,
∴E与E′重合,
∵四边形ABCD是菱形,
∴BD垂直平分AC,
∴A、C关于BD对称,
∴当P与P′重合时,P′A+P′E的值最小,最小值为CE的长=2,
故选:B.
7.D
【解析】分析:首先根据菱形的性质得出△AOD为等腰三角形,根据菱形的性质得出∠BOA=2∠AOE,结合AO=2OE得出△AOD为底角为30°角的等腰三角形,从而得出点D的坐标.
详解:∵BC∥OA, ∴∠BCO=∠COA, 又∵∠BCO=∠EAO, ∴∠COA=∠EAO,
∴△AOD为等腰三角形, ∴点D的横坐标为1, ∵四边形OACB为菱形,
∴∠BOA=2∠AOE, ∵AO=2OE, ∴∠DAO=∠DOA=30°,
∴点D的纵坐标为, ∴点D的坐标为(1,).故选D.
点睛:本题主要考查的是菱形的性质以及等腰三角形的性质,难度中等.理解菱形的性质以及得出△AOD为特殊等腰三角形是解题的关键.
8.C
【解析】试题解析:∵菱形ABCD的边长为2,
∴AD=AB=2,
又∵∠DAB=60°,
∴△DAB是等边三角形,
∴AD=BD=AB=2,
则对角线BD的长是2.
故选C.
9.C
【解析】分析:过点B作BH⊥OA,交OA于点H,利用勾股定理可求出OB的长,进而可得点A向左或向右平移的距离,由菱形的性质可知BC∥OA,所以可得向上或向下平移的距离,问题得解.
详解:过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,
过B作BH⊥x轴于H,
∵B(,1),
∴OB=,
∵A(2,0),
∴C(3,1)
∴OA=OB,
∴则四边形OACB是菱形,
∴平移点A到点C,向右平移个单位,再向上平移1个单位而得到,
故选C.
点睛:本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;
10.5或
【解析】分析:由菱形的性质证出△ABD是等边三角形,得出BD=AB=6,由勾股定理得出,即可得出答案.
详解:∵四边形ABCD是菱形,
∴AB=AD=6,AC⊥BD,OB=OD,OA=OC,
∵
∴△ABD是等边三角形,
∴BD=AB=6,
∴
∴
∴
∵点E在AC上,
∴当E在点O左边时
当点E在点O右边时
∴或;
故答案为:或.
点睛:考查菱形的性质,注意分类讨论思想在数学中的应用,不要漏解.
11.
【解析】分析:根据对角线的长度即可计算菱形的面积,根据菱形对角线互相垂直平分的性质,可以求得△AOB为直角三角形,根据AO,BO可以求得AB的值,根据菱形的面积和边长即可解题.
详解:如图,
由题意知AC=2,BD=2,
则菱形的面积S=×2×2=2,
∵菱形对角线互相垂直平分,
∴△AOB为直角三角形,AO=1,BO=,
∴AB= =2,
∴菱形的高h==.
故答案为:.
点睛:本题考查了勾股定理在直角三角形中的运用,菱形面积的计算,本题中求根据AO,BO的值求AB是解题的关键.
12.45
【解析】分析:首先证明△ABE≌△ACF,然后推出AE=AF,证明△AEF是等边三角形,最后可求出∠AFD,∠CFE的度数.
详解:连接AC,
∵菱形ABCD,∴AB=BC,∠B=∠D=60°,
∴△ABC为等边三角形,∠BCD=120°
∴AB=AC,∠ACF=∠BCD=60°,
∴∠B=∠ACF,
∵△ABC为等边三角形,
∴∠BAC=60°,即∠BAE+∠EAC=60°,
又∠EAF=60°,即∠CAF+∠EAC=60°,
∴∠BAE=∠CAF,
在△ABE与△ACF中
∴△ABE≌△ACF(ASA),
∴AE=AF,
又∠EAF=∠D=60°,则△AEF是等边三角形,
∴∠AFE=60°,
又∠AFD=180°-45°-60°=75°,
则∠CFE=180°-75°-60°=45°.
故答案为:45.
点睛:此题主要考查菱形的性质和等边三角形的判定以及三角形的内角和定理.
13.18
【解析】分析:利用菱形的性质结合勾股定理得出AB的长,进而得出答案.
详解:∵在菱形ABCD中,AC=8,BD=6,
∴AB=BC,∠AOB=90°,AO=4,BO=3,
∴BC=AB=,
∴△ABC的周长=AB+BC+AC=5+5+8=18.
故答案为:18
点睛:本题考查了菱形面积的计算,考查了勾股定理在直角三角形中的运用,考查了菱形各边长相等的性质,本题中根据勾股定理计算AB的长是解题的关键.
14.
【解析】分析:根据菱形的性质易得AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,再判定△ABD为等边三角形,根据等边三角形的性质可得AB=BD=8,从而得OB=4,在Rt△AOB中,根据勾股定理可得OA=4,继而求得AC=2AO=,再由菱形的面积公式即可求得菱形ABCD的面积.
详解:∵菱形ABCD中,其周长为32,
∴AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,
∵,
∴△ABD为等边三角形,
∴AB=BD=8,
∴OB=4,
在Rt△AOB中,OB=4,AB=8,
根据勾股定理可得OA=4,
∴AC=2AO=,
∴菱形ABCD的面积为: =.
点睛:本题考查了菱形性质:1.菱形的四个边都相等;2.菱形对角线相互垂直平分,并且每一组对角线平分一组对角;3.菱形面积公式=对角线乘积的一半.
15.
【解析】在菱形ABCD中,OC=AC,AC⊥BD,
∴DE=OC,
∵DE∥AC,
∴四边形OCED是平行四边形,
∵AC⊥BD,
∴平行四边形OCED是矩形,
∵在菱形ABCD中,∠ABC=60°,
∴△ABC为等边三角形,
∴AD=AB=AC=2,OA=AC=1,
在矩形OCED中,由勾股定理得:CE=OD===,
在Rt△ACE中,由勾股定理得:AE===;
故答案是:.
16.见解析
【解析】分析:先利用菱形的性质得出∠A=∠C,AD=CD,再结合已知条件中的垂直条件,又可得∠AED=∠CFD,从而利用AAS可证两个三角形全等.
详解:
证明:∵四边形ABCD是菱形,
∴∠A=∠C,AD=CD,
又∵DE⊥AB,DF⊥BC,
∴∠AED=∠CFD=90°,
在△ADE和△CDF中,
,
∴△ADE≌△CDF(AAS).
点睛:本题考查了菱形的性质,全等三角形的判定,解题的关键是根据菱形的性质得出两三角形全等的条件.
17.(1)证明见解析;(2).
【解析】分析:
(1)①按要求画出图形即可;②连接BD,由已知条件可知EF是△ABD的中位线,由此可得EF∥BD,由菱形的性质可得AC⊥BD,从而可得EF⊥AC;
(2)由已知条件易得△ABC是等边三角形,结合点E是AB的中点可得CE⊥AB,结合AB∥CD可得CE⊥MC,在Rt△BCE中由已知条件求得CE的长,由已知易得AE=1,由此可得MD=1,从而可得CD的长,这样即可由S△CME=MC·CE求出其面积了.
详解:
(1)①补全图形如下图所示:
②如下图,连接DB,
∵四边形ABCD是菱形,
∴DB⊥AC,
∵E,F分别是AB,AD的中点,
∴EF∥BD.
∴EF⊥AC.
(2)∵四边形ABCD是菱形,
∴AB=BC.
∵∠B=60°,
∴△ABC是等边三角形,
∵E是AB的中点,
∴CE⊥AB,CE⊥MC.
即△EMC是直角三角形,且CE=BC×sin60°=.
由(1)得MD=AE=AB=1.
∴MC=MD+DC=3.
∴S△EMC=MC×CE=.
点睛:(1)解第1小题时,连接BD,证得EF是三角形ABD的中位线得到EF∥BD是解答本问的关键;(2)解第2小题时,证得△ABC是等边三角形,结合点E是AB边的中点得到CE⊥AB,从而得到CE⊥MC是解题的关键.
18.(1)见解析;(2)5
【解析】分析:(1)利用平行四边形的性质得出AF∥EC,进而得出AF=EC,进而求出即可;
(2)利用菱形的性质以及三角形内角和定理得出∠1=∠2,进而求出∠3=∠4,再利用直角三角形的性质得出答案.
详解:证明:四边形ABCD是平行四边形,
,且,
,
,
,
四边形AECF是平行四边形.
解:四边形AECF是菱形,
,
,
,
,,
,
,
.
点睛:此题主要考查了平行四边形的性质与判定,平行线的性质,菱形的性质,直角三角形的性质,等腰三角形的判定,得出∠3=∠4是解答本题的关键.
19.(1)见解析;(2)2
【解析】分析:(1)由四边形ABCD是菱形,可得AB∥CD,OA=OC,继而证得△AOE≌△COF,则可证得结论.
(2)利用平行四边形的判定和性质解答即可.
详解:(1)∵四边形ABCD是菱形,
∴AO=CO,AB∥CD,
∴∠EAO=∠FCO,∠AEO=∠CFO.
在△OAE和△OCF中,
∠EAO=∠FCO,AO=CO,∠AEO=∠CFO,
∴△AOE≌△COF,
∴AE=CF;
(2)∵E是AB中点,
∴BE=AE=CF.
∵BE∥CF,
∴四边形BEFC是平行四边形,
∵AB=2,
∴EF=BC=AB=2.
点睛:此题考查了菱形的性质以及全等三角形的判定与性质.此题难度不大,注意掌握数形结合思想的应用.
20.(1) EH2+CH2=AE2;(2)见解析.
【解析】分析:(1)如图1,过E作EM⊥AD于M,由四边形ABCD是菱形,得到AD=CD,∠ADE=∠CDE,通过△DME≌△DHE,根据全等三角形的性质得到EM=EH,DM=DH,等量代换得到AM=CH,根据勾股定理即可得到结论;
(2)如图2,根据菱形的性质得到∠BDC=∠BDA=30°,DA=DC,在CH上截取HG,使HG=EH,推出△DEG是等边三角形,由等边三角形的性质得到∠EDG=60°,推出△DAE≌△DCG,根据全等三角形的性质即可得到结论.
详解:
(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
故答案为:EH2+CH2=AE2;
(2)如图2,
∵菱形ABCD,∠ADC=60°,
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG﹣∠ADG=∠ADC﹣∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,
,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.
点睛:考查了全等三角形的判定和性质、菱形的性质、旋转的性质、等边三角形的判定和性质,解题的关键是正确的作出辅助线.
21.(1)5;(2)直线AC的解析式y=﹣x+;(3)见解析.
【解析】分析:(1)Rt△AOH中利用勾股定理即可求得菱形的边长;
(2)根据(1)即可求的OC的长,则C的坐标即可求得,利用待定系数法即可求得直线AC的解析式;
(3)根据S△ABC=S△AMB+S△BMC求得M到直线BC的距离为h,然后分成P在AM上和在MC上两种情况讨论,利用三角形的面积公式求解.
详解:(1)Rt△AOH中,
AO===5,
所以菱形边长为5;
故答案为:5;
(2)∵四边形ABCO是菱形,
∴OC=OA=AB=5,即C(5,0).
设直线AC的解析式y=kx+b,函数图象过点A、C,得
,解得,
直线AC的解析式y=﹣x+;
(3)设M到直线BC的距离为h,
当x=0时,y=,即M(0,),HM=HO﹣OM=4﹣=,
由S△ABC=S△AMB+SBMC=AB OH=AB HM+BC h,
×5×4=×5×+×5h,解得h=,
①当0<t<时,BP=BA﹣AP=5﹣2t,HM=OH﹣OM=,
S=BP HM=×(5﹣2t)=﹣t+;
②当2.5<t≤5时,BP=2t﹣5,h=,
S=BP h=×(2t﹣5)=t﹣,
把S=3代入①中的函数解析式得,3=﹣t+,
解得:t=,
把S=3代入②的解析式得,3=t﹣,
解得:t=.
∴t=或.
点睛:本题考查了待定系数法求一次函数的解析式以及菱形的性质,根据三角形的面积关系求得M到直线BC的距离h是关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
