1.1 菱形的性质与判定(2)同步作业
文档属性
| 名称 | 1.1 菱形的性质与判定(2)同步作业 |  | |
| 格式 | docx | ||
| 文件大小 | 516.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-19 12:23:43 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.1 菱形的性质与判定(2)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.如图,在 ABCD中,对角线相交于点O,添加下列条件不能判定 ABCD是菱形的只有( )
A. B. C. D.
2.下列命题中正确的是( )
A. 对角线相等的四边形是菱形 B. 对角线互相垂直的四边形是菱形
C. 对角线相等的平行四边形是菱形 D. 对角线互相垂直的平行四边形是菱形
3.已知四边形ABCD是平行四边形,如果要使它成为菱形,那么需要添加的条件是( )
A. ; B. ; C. ; D. .
4.四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
5.在平面直角坐标系中,已知点A(0,2),B(﹣2,0),C(0,﹣2),D(2,0),则以这四个点为顶点的四边形ABCD是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
6.红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示.红丝带重叠部分形成的图形是( )
A. 正方形 B. 等腰梯形 C. 菱形 D. 矩形
7.如图,在平面直角坐标系xOy中,已知点A(,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
A. 向左平移1个单位,再向下平移1个单位
B. 向左平移()个单位,再向上平移1个单位
C. 向右平移个单位,再向上平移1个单位
D. 向右平移1个单位,再向上平移1个单位
8.如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:
对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确 C. 甲、乙均正确 D. 甲、乙均错误
9.如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
A. AD平分∠MAN B. AD垂直平分BC C. ∠MBD=∠NCD D. 四边形ACDB一定是菱形
二、填空题
10.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形.如(1)(2)(5) ABCD是菱形,再写出符合要求的两个:__________ ABCD是菱形;_________ ABCD是菱形.
11.如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是____cm2.
12.如图,在ABCD中,对角线AC,BD相交于点O,若再增加一个条件,就可得出ABCD是菱形,则你添加的条件是___________.
13.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的形状是__________.
14.在数学课上,老师提出如下问题:
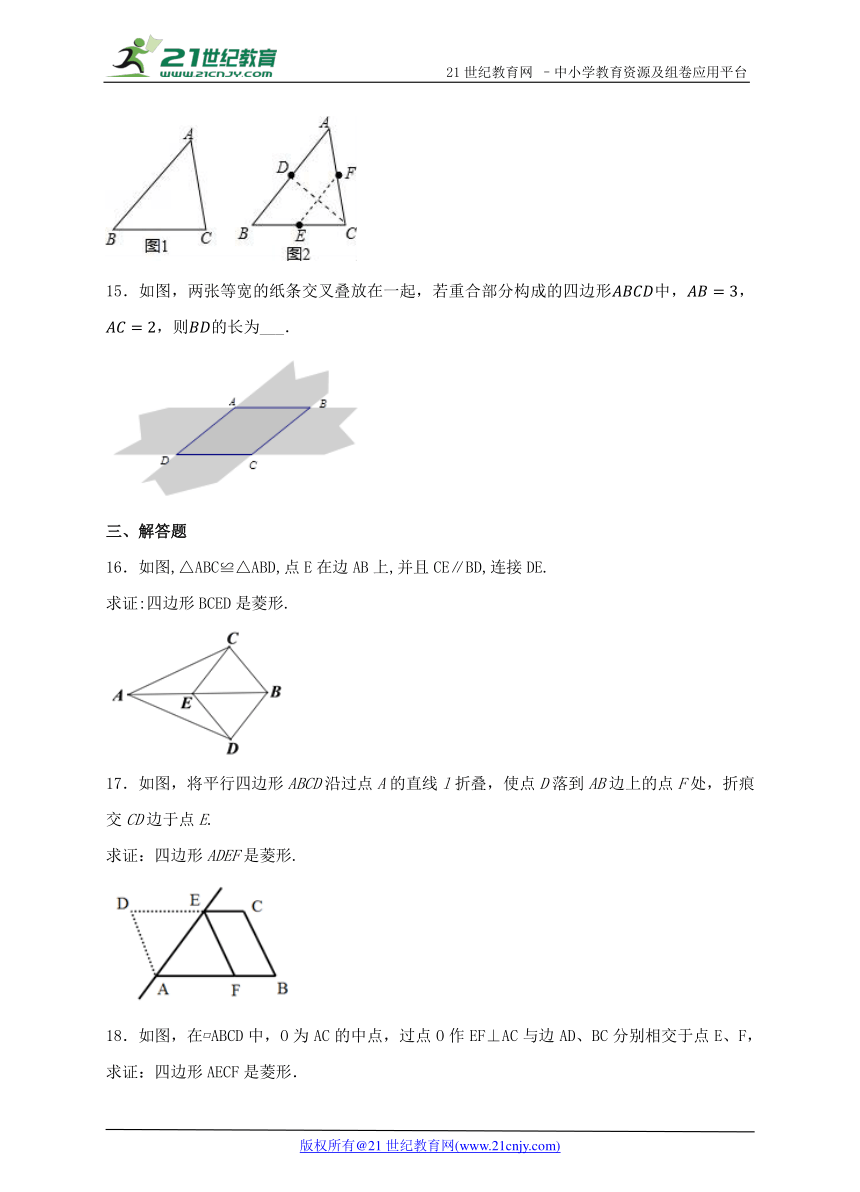
如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是 ____________________.
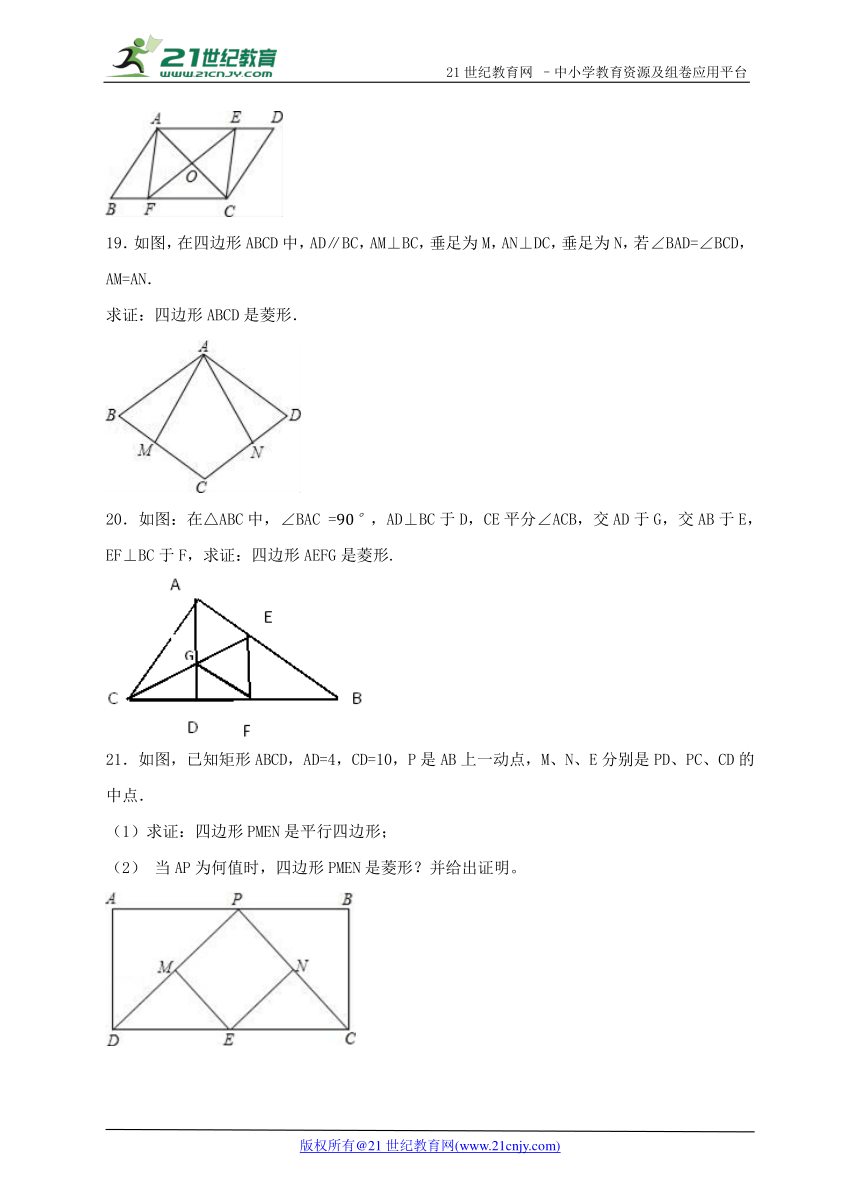
15.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形中,,,则的长为___.
三、解答题
16.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE.
求证:四边形BCED是菱形.
17.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E.
求证:四边形ADEF是菱形.
18.如图,在 ABCD中,O为AC的中点,过点O作EF⊥AC与边AD、BC分别相交于点E、F,求证:四边形AECF是菱形.
19.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN.
求证:四边形ABCD是菱形.
20.如图:在△ABC中,∠BAC =,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
21.如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。
参考答案
1.C
【解析】因为对角线互相垂直的平行四边形是菱形,所以A能够判定 ABCD是菱形;因为一组邻边相等的平行四边形是菱形,所以B能够判定 ABCD是菱形;因为对角线相等的平行四边形是矩形,所以C不能够判定 ABCD是菱形;因为∠1=∠2,OB=OD,所以AB=AD,所以D能够判定 ABCD是菱形,故选C.
2.D
【解析】试题分析:在一个平面内,一组邻边相等的平行四边形是菱形。对角线相互垂直的平行四边形是菱形,四条边都相等的四边形是菱形。故选D
3.B
【解析】分析:由四个选项均为相等的线段这一条件,根据菱形定义:一组邻边相等的平行四边形是菱形,即可判断出所添加的条件.
详解:∵四边形ABCD是平行四边形,
当时,
平行四边形ABCD是菱形.
∴添加的条件为:.
故选B.
点睛:本题考查了菱形的判定方法. 结合选项并根据菱形的判定方法来选取所添加的条件是解题的关键.
4.C
【解析】试题解析:整理配方式子
由非负数的性质可知:
∴四边形一定是菱形,
故选C.
5.B
【解析】试题解析:在平面直角坐标系中画出图后,可发现这个四边形的对角线互相平分,先判断为平行四边形,对角线还垂直,那么这样的平行四边形应是菱形.
故选B.
6.C
【解析】试题解析:
过点A作于E,于F,因为两条彩带宽度相同,
所以AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
又
∴四边形ABCD是菱形.
故选C.
点睛:首先可判断重叠部分为平行四边形,且两条彩带宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.
点睛:菱形的判定方法:有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
7.D
【解析】过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,
过B作DH⊥x轴于H,
∵B(1,1),
∴OB= ,
∵A( ,0),
∴C(1+,1)
∴OA=OB,
∴则四边形OACB是菱形,
∴平移点A到点C,向右平移1个单位,再向上平移1个单位而得到,
故选D.
8.C
【解析】试题解析:根据甲的作法作出图形,如下图所示.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EF是AC的垂直平分线,
在和中,
∴≌,
又∵AE∥CF,
∴四边形AECF是平行四边形.
∴四边形AECF是菱形.
故甲的作法正确.
根据乙的作法作出图形,如下图所示.
∵AD∥BC,
∴∠1=∠2,∠6=∠7.
∵BF平分,AE平分
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∵AF∥BE,且
∴四边形ABEF是平行四边形.
∵
∴平行四边形ABEF是菱形.
故乙的作法正确.
故选C.
点睛:菱形的判定方法:有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边相等的平行四边形是菱形.
9.D
【解析】试题解析:A、由作法可得AD平分∠MAN,所以A选项的结论正确;
B、因为AB=AC,DB=DC,所以AD垂直平分BC,所以B选项的结论正确;
C、因为AB=AC,DB=DC,所以∠ABC=∠ACB,∠DBC=∠DCB,则∠ABD=∠ACD,所以∠MBD=∠NCD,所以C选项的结论正确;
D、BA不一定等于BD,所以四边形ABDC不一定是菱形,所以D选项的结论错误.
故选D.
10. (1)(2)(6), (3)(4)(5)或者(3)(4)(6)
【解析】试题解析:菱形的判定方法有三种:
定义:一组邻边相等的平行四边形是菱形;
四边相等;
③对角线互相垂直平分的四边形是菱形.
(1)(2)(6) ABCD是菱形.
先由(1)(2)得出四边形是平行四边形,
再由(6)和(2)得出
由等角对等边得
所以平行四边形是菱形.
(3)(4)(5) ABCD是菱形.
由对角线互相平分且垂直的四边形是菱形.
(3)(4)(6) ABCD是菱形.
由(3)(4)得出四边形是平行四边形,
再由(6)得出
由等角对等边得
所以平行四边形是菱形.
故答案为:
11.8
【解析】∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,
分别作CD,BC边上的高为AE,AF,如图所示:
∵两纸条相同,∴纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,∴CD=BC.∴平行四边形ABCD为菱形,
∴AB=AD=4cm,
∵∠ABC=30°,∴AE=AB=2cm,∴S菱形ABCD=BC AE=4×2=8,
故答案为8.
12.AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA
【解析】根据一组邻边相等的平行四边形是菱形可得,添加的条件可以是:AB=BC或BC=CD或CD=AD或AD=AB;
根据对角线互相垂直的平行四边形是菱形可得,添加的条件可以是:AC⊥BD;
根据四边相等的平行四边形是菱形可得,添加的条件可以是:AB=BC=CD=DA.
故答案是:AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA.
13.菱形
【解析】根据题意,DE∥AC,DF∥AB,
则四边形AEDF是平行四边形,
又∵AD是△ABC的角平分线,
∴∠EAD=∠DAF=∠ADE,
则AE=ED,
即四边形AEDF是菱形.
故答案是:菱形.
14.对角线互相垂直平分的四边形是菱形
【解析】对角线互相垂直平分的四边形是菱形
15.
【解析】
连接AC,BD由题意得,四边形ABCD是菱形,∴AO=1,AC⊥BD.
由勾股定理得, , .
16.见解析
【解析】分析:根据≌得到证明≌,得到,
根据平行线的性质证明,得到,即可证明四边形BCED是菱形.
详解:∵≌,
∴ ,
在和中
,
∴≌ ,
∴,
又∵,
∴ ,
∴,
∴,
∴,
∴四边形BCED是菱形.
点睛:考查菱形的判定方法,常见的判定方法有:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
17.证明见解析
【解析】分析:利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论.
详解:证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA
∵四边形ABCD是平行四边形
∴DE∥AF
∴∠DEA=∠EAF
∴∠EAF=∠FEA
∴AF=EF
∴AF=AD=DE=EF
∴四边形ADEF是菱形.
点睛:本题考查了平行四边形的性质,菱形的判定和性质,理解性质和判定是解题的关键.
18.见解析
【解析】分析:先判定△AOE≌△COF得到AE=CF,,再根据AE∥CF,即可得到四边形AECF是平行四边形,最后根据EF与AC垂直,得到四边形AECF是菱形.
详解:证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴AE∥CF,
∴∠OAE=∠OCF,
∵点O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF与AC垂直,
∴四边形AECF是菱形
点睛:考查菱形的判定,熟记菱形的判定方法是解题的关键.
19.证明见解析
【解析】分析:首先证明,可得四边形是平行四边形,然后再证明≌可得,再根据菱形的判定定理可得结论.
详解:证明:∵AD∥BC,
∴,
∵∠BAD=∠BCD,
∴∠B=∠D,
∴四边形ABCD是平行四边形,
∵AM⊥BC,AN⊥DC,
∴
在△ABM和△ADN中,
∴△ABM≌△ADN(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
点睛:考查菱形的判定,掌握判定方法是解题的关键.
20.证明见解析.
【解析】分析:根据三角形内角和定理求出∠B=∠CAD,根据角平分线性质求出AE=EF,由勾股定理求出AC=CF,证△ACG≌△FCG,推出∠CAD=∠CFG,得出∠B=∠CFG,推出GF∥AB,AD∥EF,得出平行四边形,根据菱形的判定判断即可.
详解:证明:∵AD⊥BC,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),
∴AE=EF(角平分线上的点到角两边的距离相等),
∵CE=CE,∴由勾股定理得:AC=CF,
∵△ACG和△FCG中
∴△ACG≌△FCG,
∴∠CAD=∠CFG,
∵∠B=∠CAD,
∴∠B=∠CFG,
∴GF∥AB,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,
∵AE=EF,
∴平行四边形AEFG是菱形.
点睛:本题考查了平行四边形的性质和判定,菱形的判定,勾股定理,全等三角形的性质和判定的应用,通过做此题培养了学生的推理能力,题目比较好,综合性也比较强.
21.(1)证明见解析;(2)当PA=5时,四边形PMEN为菱形,理由见解析.
【解析】分析:(1)用三角形的中位线定理证明四边形PMEN的两组对边分别平行;(2)由(1)得四边形PMEN是平行四边形,只需证PM=PN,即PC=PD,故要证△APD≌△BPC.
详解:(1)∵M,E分别为PD,CD的中点,∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形;
(2)当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,∴AP=BP,
在△APD和△BPC中,
AP=BP,∠A=∠B,AD=BC,
∴△APD≌△BPC(SAS),∴PD=PC,
∵M,N,E分别是PD,PC,CD的中点,
∴EN=PM=PD,PN=EM=PC,∴PM=EM=EN=PN,
∴四边形PMEN是菱形.
点睛:本题考查了平行四边形,菱形的判定和矩形的性质,三角形的中位定理反应了两条线段之间的数量关系与位置关系,所以,当题中有多个中点时,常常考虑用三角形的中位线来解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
1.1 菱形的性质与判定(2)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.如图,在 ABCD中,对角线相交于点O,添加下列条件不能判定 ABCD是菱形的只有( )
A. B. C. D.
2.下列命题中正确的是( )
A. 对角线相等的四边形是菱形 B. 对角线互相垂直的四边形是菱形
C. 对角线相等的平行四边形是菱形 D. 对角线互相垂直的平行四边形是菱形
3.已知四边形ABCD是平行四边形,如果要使它成为菱形,那么需要添加的条件是( )
A. ; B. ; C. ; D. .
4.四边形的四边长顺次为a、b、c、d,且a2+b2+c2+d2=ab+bc+cd+ad,则此四边形一定是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 正方形
5.在平面直角坐标系中,已知点A(0,2),B(﹣2,0),C(0,﹣2),D(2,0),则以这四个点为顶点的四边形ABCD是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
6.红丝带是关注艾滋病防治问题的国际性标志,人们将红丝带剪成小段,并用别针将折叠好的红丝带别在胸前,如图所示.红丝带重叠部分形成的图形是( )
A. 正方形 B. 等腰梯形 C. 菱形 D. 矩形
7.如图,在平面直角坐标系xOy中,已知点A(,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
A. 向左平移1个单位,再向下平移1个单位
B. 向左平移()个单位,再向上平移1个单位
C. 向右平移个单位,再向上平移1个单位
D. 向右平移1个单位,再向上平移1个单位
8.如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:
对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确 C. 甲、乙均正确 D. 甲、乙均错误
9.如图,以A点为圆心,以相同的长为半径作弧,分别与射线AM,AN交于B,C两点,连接BC,再分别以B,C为圆心,以相同长(大于BC)为半径作弧,两弧相交于点D,连接AD,BD,CD.则下列结论错误的是( )
A. AD平分∠MAN B. AD垂直平分BC C. ∠MBD=∠NCD D. 四边形ACDB一定是菱形
二、填空题
10.在四边形ABCD中,对角线AC、BD交于点O,从(1)AB=CD;(2)AB∥CD;(3)OA=OC;(4)OB=OD;(5)AC⊥BD;(6)AC平分∠BAD这六个条件中,选取三个推出四边形ABCD是菱形.如(1)(2)(5) ABCD是菱形,再写出符合要求的两个:__________ ABCD是菱形;_________ ABCD是菱形.
11.如图所示,将两张等宽的长方形条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则四边形ABCD的面积是____cm2.
12.如图,在ABCD中,对角线AC,BD相交于点O,若再增加一个条件,就可得出ABCD是菱形,则你添加的条件是___________.
13.如图,DE∥AC交AB于点E,DF∥AB交AC于F,∠1=∠2,四边形AEDF的形状是__________.
14.在数学课上,老师提出如下问题:
如图1,将锐角三角形纸片ABC(BC>AC)经过两次折叠,得到边AB,BC,CA上的点D,E,F.使得四边形DECF恰好为菱形.小明的折叠方法如下:
如图2,(1)AC边向BC边折叠,使AC边落在BC边上,得到折痕交AB于D; (2)C点向AB边折叠,使C点与D点重合,得到折痕交BC边于E,交AC边于F.
老师说:“小明的作法正确.”
请回答:小明这样折叠的依据是 ____________________.
15.如图,两张等宽的纸条交叉叠放在一起,若重合部分构成的四边形中,,,则的长为___.
三、解答题
16.如图,△ABC≌△ABD,点E在边AB上,并且CE∥BD,连接DE.
求证:四边形BCED是菱形.
17.如图,将平行四边形ABCD沿过点A的直线l折叠,使点D落到AB边上的点F处,折痕交CD边于点E.
求证:四边形ADEF是菱形.
18.如图,在 ABCD中,O为AC的中点,过点O作EF⊥AC与边AD、BC分别相交于点E、F,求证:四边形AECF是菱形.
19.如图,在四边形ABCD中,AD∥BC,AM⊥BC,垂足为M,AN⊥DC,垂足为N,若∠BAD=∠BCD,AM=AN.
求证:四边形ABCD是菱形.
20.如图:在△ABC中,∠BAC =,AD⊥BC于D,CE平分∠ACB,交AD于G,交AB于E,EF⊥BC于F,求证:四边形AEFG是菱形.
21.如图,已知矩形ABCD,AD=4,CD=10,P是AB上一动点,M、N、E分别是PD、PC、CD的中点.
(1)求证:四边形PMEN是平行四边形;
(2) 当AP为何值时,四边形PMEN是菱形?并给出证明。
参考答案
1.C
【解析】因为对角线互相垂直的平行四边形是菱形,所以A能够判定 ABCD是菱形;因为一组邻边相等的平行四边形是菱形,所以B能够判定 ABCD是菱形;因为对角线相等的平行四边形是矩形,所以C不能够判定 ABCD是菱形;因为∠1=∠2,OB=OD,所以AB=AD,所以D能够判定 ABCD是菱形,故选C.
2.D
【解析】试题分析:在一个平面内,一组邻边相等的平行四边形是菱形。对角线相互垂直的平行四边形是菱形,四条边都相等的四边形是菱形。故选D
3.B
【解析】分析:由四个选项均为相等的线段这一条件,根据菱形定义:一组邻边相等的平行四边形是菱形,即可判断出所添加的条件.
详解:∵四边形ABCD是平行四边形,
当时,
平行四边形ABCD是菱形.
∴添加的条件为:.
故选B.
点睛:本题考查了菱形的判定方法. 结合选项并根据菱形的判定方法来选取所添加的条件是解题的关键.
4.C
【解析】试题解析:整理配方式子
由非负数的性质可知:
∴四边形一定是菱形,
故选C.
5.B
【解析】试题解析:在平面直角坐标系中画出图后,可发现这个四边形的对角线互相平分,先判断为平行四边形,对角线还垂直,那么这样的平行四边形应是菱形.
故选B.
6.C
【解析】试题解析:
过点A作于E,于F,因为两条彩带宽度相同,
所以AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形.
又
∴四边形ABCD是菱形.
故选C.
点睛:首先可判断重叠部分为平行四边形,且两条彩带宽度相同;再由平行四边形的面积可得邻边相等,则重叠部分为菱形.
点睛:菱形的判定方法:有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
7.D
【解析】过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,
过B作DH⊥x轴于H,
∵B(1,1),
∴OB= ,
∵A( ,0),
∴C(1+,1)
∴OA=OB,
∴则四边形OACB是菱形,
∴平移点A到点C,向右平移1个单位,再向上平移1个单位而得到,
故选D.
8.C
【解析】试题解析:根据甲的作法作出图形,如下图所示.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∵EF是AC的垂直平分线,
在和中,
∴≌,
又∵AE∥CF,
∴四边形AECF是平行四边形.
∴四边形AECF是菱形.
故甲的作法正确.
根据乙的作法作出图形,如下图所示.
∵AD∥BC,
∴∠1=∠2,∠6=∠7.
∵BF平分,AE平分
∴∠2=∠3,∠5=∠6,
∴∠1=∠3,∠5=∠7,
∵AF∥BE,且
∴四边形ABEF是平行四边形.
∵
∴平行四边形ABEF是菱形.
故乙的作法正确.
故选C.
点睛:菱形的判定方法:有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边相等的平行四边形是菱形.
9.D
【解析】试题解析:A、由作法可得AD平分∠MAN,所以A选项的结论正确;
B、因为AB=AC,DB=DC,所以AD垂直平分BC,所以B选项的结论正确;
C、因为AB=AC,DB=DC,所以∠ABC=∠ACB,∠DBC=∠DCB,则∠ABD=∠ACD,所以∠MBD=∠NCD,所以C选项的结论正确;
D、BA不一定等于BD,所以四边形ABDC不一定是菱形,所以D选项的结论错误.
故选D.
10. (1)(2)(6), (3)(4)(5)或者(3)(4)(6)
【解析】试题解析:菱形的判定方法有三种:
定义:一组邻边相等的平行四边形是菱形;
四边相等;
③对角线互相垂直平分的四边形是菱形.
(1)(2)(6) ABCD是菱形.
先由(1)(2)得出四边形是平行四边形,
再由(6)和(2)得出
由等角对等边得
所以平行四边形是菱形.
(3)(4)(5) ABCD是菱形.
由对角线互相平分且垂直的四边形是菱形.
(3)(4)(6) ABCD是菱形.
由(3)(4)得出四边形是平行四边形,
再由(6)得出
由等角对等边得
所以平行四边形是菱形.
故答案为:
11.8
【解析】∵AD∥BC,AB∥CD,∴四边形ABCD是平行四边形,
分别作CD,BC边上的高为AE,AF,如图所示:
∵两纸条相同,∴纸条宽度AE=AF.
∵平行四边形的面积为AE×CD=BC×AF,∴CD=BC.∴平行四边形ABCD为菱形,
∴AB=AD=4cm,
∵∠ABC=30°,∴AE=AB=2cm,∴S菱形ABCD=BC AE=4×2=8,
故答案为8.
12.AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA
【解析】根据一组邻边相等的平行四边形是菱形可得,添加的条件可以是:AB=BC或BC=CD或CD=AD或AD=AB;
根据对角线互相垂直的平行四边形是菱形可得,添加的条件可以是:AC⊥BD;
根据四边相等的平行四边形是菱形可得,添加的条件可以是:AB=BC=CD=DA.
故答案是:AB=BC或BC=CD或CD=AD或AD=AB或AC⊥BD或AB=BC=CD=DA.
13.菱形
【解析】根据题意,DE∥AC,DF∥AB,
则四边形AEDF是平行四边形,
又∵AD是△ABC的角平分线,
∴∠EAD=∠DAF=∠ADE,
则AE=ED,
即四边形AEDF是菱形.
故答案是:菱形.
14.对角线互相垂直平分的四边形是菱形
【解析】对角线互相垂直平分的四边形是菱形
15.
【解析】
连接AC,BD由题意得,四边形ABCD是菱形,∴AO=1,AC⊥BD.
由勾股定理得, , .
16.见解析
【解析】分析:根据≌得到证明≌,得到,
根据平行线的性质证明,得到,即可证明四边形BCED是菱形.
详解:∵≌,
∴ ,
在和中
,
∴≌ ,
∴,
又∵,
∴ ,
∴,
∴,
∴,
∴四边形BCED是菱形.
点睛:考查菱形的判定方法,常见的判定方法有:
有一组邻边相等的平行四边形是菱形.
对角线互相垂直的平行四边形是菱形.
四条边都相等的四边形是菱形.
17.证明见解析
【解析】分析:利用翻折变换的性质以及平行线的性质得出∠DAE=∠EAD′=∠DEA=∠D′EA,进而利用平行四边形的判定方法得出四边形DAD′E是平行四边形,进而求出四边形BCED′是平行四边形,根据折叠的性质得到AD=AD′,然后又菱形的判定定理即可得到结论.
详解:证明:由折叠可知,DE=EF,AD=AF,∠DEA=∠FEA
∵四边形ABCD是平行四边形
∴DE∥AF
∴∠DEA=∠EAF
∴∠EAF=∠FEA
∴AF=EF
∴AF=AD=DE=EF
∴四边形ADEF是菱形.
点睛:本题考查了平行四边形的性质,菱形的判定和性质,理解性质和判定是解题的关键.
18.见解析
【解析】分析:先判定△AOE≌△COF得到AE=CF,,再根据AE∥CF,即可得到四边形AECF是平行四边形,最后根据EF与AC垂直,得到四边形AECF是菱形.
详解:证明:∵四边形ABCD是平行四边形,
∴BC∥AD,
∴AE∥CF,
∴∠OAE=∠OCF,
∵点O是AC的中点,
∴OA=OC,
在△AOE和△COF中,
∴△AOE≌△COF(ASA),
∴AE=CF,
∵AE∥CF,
∴四边形AECF是平行四边形,
∵EF与AC垂直,
∴四边形AECF是菱形
点睛:考查菱形的判定,熟记菱形的判定方法是解题的关键.
19.证明见解析
【解析】分析:首先证明,可得四边形是平行四边形,然后再证明≌可得,再根据菱形的判定定理可得结论.
详解:证明:∵AD∥BC,
∴,
∵∠BAD=∠BCD,
∴∠B=∠D,
∴四边形ABCD是平行四边形,
∵AM⊥BC,AN⊥DC,
∴
在△ABM和△ADN中,
∴△ABM≌△ADN(AAS),
∴AB=AD,
∴四边形ABCD是菱形.
点睛:考查菱形的判定,掌握判定方法是解题的关键.
20.证明见解析.
【解析】分析:根据三角形内角和定理求出∠B=∠CAD,根据角平分线性质求出AE=EF,由勾股定理求出AC=CF,证△ACG≌△FCG,推出∠CAD=∠CFG,得出∠B=∠CFG,推出GF∥AB,AD∥EF,得出平行四边形,根据菱形的判定判断即可.
详解:证明:∵AD⊥BC,
∴∠ADB=90°,
∵∠BAC=90°,
∴∠B+∠BAD=90°,∠BAD+∠CAD=90°,
∴∠B=∠CAD,
∵CE平分∠ACB,EF⊥BC,∠BAC=90°(EA⊥CA),
∴AE=EF(角平分线上的点到角两边的距离相等),
∵CE=CE,∴由勾股定理得:AC=CF,
∵△ACG和△FCG中
∴△ACG≌△FCG,
∴∠CAD=∠CFG,
∵∠B=∠CAD,
∴∠B=∠CFG,
∴GF∥AB,
∵AD⊥BC,EF⊥BC,
∴AD∥EF,
即AG∥EF,AE∥GF,
∴四边形AEFG是平行四边形,
∵AE=EF,
∴平行四边形AEFG是菱形.
点睛:本题考查了平行四边形的性质和判定,菱形的判定,勾股定理,全等三角形的性质和判定的应用,通过做此题培养了学生的推理能力,题目比较好,综合性也比较强.
21.(1)证明见解析;(2)当PA=5时,四边形PMEN为菱形,理由见解析.
【解析】分析:(1)用三角形的中位线定理证明四边形PMEN的两组对边分别平行;(2)由(1)得四边形PMEN是平行四边形,只需证PM=PN,即PC=PD,故要证△APD≌△BPC.
详解:(1)∵M,E分别为PD,CD的中点,∴ME∥PC,
同理可证:ME∥PD,
∴四边形PMEN为平行四边形;
(2)当PA=5时,四边形PMEN为菱形.
理由:∵四边形ABCD是矩形,∴∠A=∠B=90°,AD=BC,
∵AP=5,AB=CD=10,∴AP=BP,
在△APD和△BPC中,
AP=BP,∠A=∠B,AD=BC,
∴△APD≌△BPC(SAS),∴PD=PC,
∵M,N,E分别是PD,PC,CD的中点,
∴EN=PM=PD,PN=EM=PC,∴PM=EM=EN=PN,
∴四边形PMEN是菱形.
点睛:本题考查了平行四边形,菱形的判定和矩形的性质,三角形的中位定理反应了两条线段之间的数量关系与位置关系,所以,当题中有多个中点时,常常考虑用三角形的中位线来解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
