数学六年级下北师大版总复习 式与方程课件 (共49张)
文档属性
| 名称 | 数学六年级下北师大版总复习 式与方程课件 (共49张) |  | |
| 格式 | zip | ||
| 文件大小 | 919.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-20 16:07:03 | ||
图片预览











文档简介
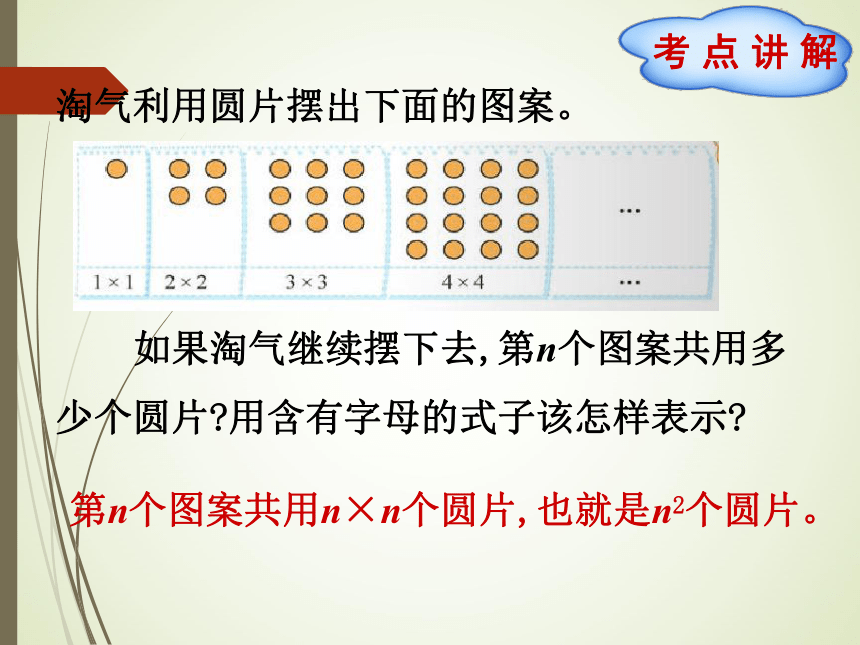
课件49张PPT。六年级数学·下 新课标[北师]总 复 习1 数与代数第8课时 式与方程淘气利用圆片摆出下面的图案。 如果淘气继续摆下去,第n个图案共用多少个圆片?用含有字母的式子该怎样表示?第n个图案共用n×n个圆片,也就是n2个圆片。加法交换律:a+b=b+a
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c长方形的周长和面积公式:C=(a+b)×2 S=ab
正方形的周长和面积公式:C=4a S=a·a=a2
三角形的面积公式:S=ah÷2
平行四边形的面积公式:S=ah
梯形的面积公式:S=(a+b)h÷2
圆的周长和面积公式:C=πd或C=2πr S=πr2正方体的表面积和体积公式:
S=6a2 V=a·a·a=a3
长方体的体积公式:V=abh
圆柱的体积公式:V=Sh=πr2h
圆锥的体积公式:V= Sh= πr2h用字母表示数注意的问题:1.在含有字母的式子里,字母就读字母的名称,
字母与字母、字母与数字之间的乘号可以记
作“·”或省略不写。但要注意,在省略乘号
的时候,应当把数字写在字母的前面。
例如:a×4=4·a(或4a),n×m=n·m(或nm),
5×b×c=5·b·c(或5bc)。用字母表示数注意的问题:2.用字母表示除法、分数和比时,表示除数、分
母及比的后项的字母不能为0。3.用字母表示运算结果时,必须是最简单的式子。例1 如果速度用v表示、时间用t表示、路程用s表示,请你用字母表示它们之间的关系。S=vt练习一个长方形,它的长是宽的4倍。(1)如果宽是a厘米,那么长方形的周长是多少?周长:2×(4a+a)=10a(厘米)(2)在第(1)问的情况下,如果a=5,那么长方形的周
长和面积各是多少?周长:10a=10×5=50(厘米)面积:20×5=100(平方厘米)表示相等关系的式子叫等式。 等式的性质:等式两边同时加上或减去相同的一个数,等式仍然成立。等式的两边同时乘或除以相同的一个数(0除外),等式仍然成立。含有未知数的等式叫作方程。 使方程左右两边相等的未知数的值叫作方程的解。求方程的解的过程叫解方程。3.解下面的方程,并说一说你是怎么解的。9x-1.8=5.40.8x+1.2x=25解:9x=5.4+1.89x=7.2x=7.2÷9x=0.8解:2x=25x=25÷2x=12.5 方法1:直接根据四则运算中已知数与得数之间的关系,求未知数的值。 方法2:根据等式的性质计算。例2解方程:60%x-2×4=10.6。解法一解: 60%x-8=10.6
60%x=10.6+8
60%x=18.6
x=18.6÷0.6
x=31例2解方程:60%x-2×4=10.6。解法二解: 60%x-8=10.6
60%x-8+8=10.6+8,
60%x=10.6+8
60%x=18.6
60%x÷60%=18.6÷60%
x=18.6÷0.6
x=31练习解方程0.6x-2×4=52。解: 0.6x-8+8=52+8
0.6x=60
0.6x÷0.6=60÷0.6
x=1004.列方程解决下列问题。(1)果品商店购进20箱苹果,购进苹果的箱数是
橘子箱数的 。商店购进了多少箱橘子?解:设商店购进了x箱橘子。答:商店购进了25箱橘子。(2)妙想、乐乐各收集了多少枚邮票?解:设乐乐收集了x枚邮票。
x+3x=128
x=3232×3=96(枚)答:妙想收集了96枚,乐乐收集了32枚。(3)淘气家和奇思家相距1240 m。一天,两人约
定在两家之间的路上回合。淘气每分走75 m,
奇思每分走80 m。两人同时从家出发,多长
时间后能相遇?解:设x分后能相遇。
75x+80x=1240
x=8答:8分后能相遇。例3 笑笑到文具店去买铅笔。如果买5支,还剩0.3元;如果买6支,则差0.2元。笑笑带了多少元钱?解:设每支铅笔的价钱为x元。
5x+0.3=6x-0.2
x=0.5
5×0.5+0.3=2.8(元)或6×0.5-0.2=2.8(元)
答:笑笑带了2.8元钱。 利民超市原来有一些饺子粉,每袋5千克,卖出7袋以后,还剩40千克。这个超市原来有多少千克饺子粉?(用方程解)解:设这个超市原来有x千克饺子粉。
x-5×7=40
x-35+35=40+35
x=75
答:这个超市原来有75千克饺子粉。列方程解应用题的一般步骤:1.分析题意,明确题中的数量关系。2.用字母(x或y)表示题中的未知数。设未知数的
方法有两种:一种是直接设定,即题中求什么就
设什么;二是间接设定,先设某一个数为x后,通
过这个数去求所求的未知数。列方程解应用题的一般步骤:3.找出题中数量间的等量关系,并根据等量关系
列方程。4.解方程,求出未知数的值。5.可以检验,之后写出答语。1.填一填。 教材第81页“巩固与应用”第1题 。(1)比x少25的数是 。(2)n的5倍与m的差是 。(3)一件衬衫a元,一件毛衣的价格比它的2倍
还多6元,毛衣的价格是 元。(4)原价a元的产品打八折后的价钱是 元。x-255n-m2a+680%a4.摆正方形。 教材第81页“巩固与应用”第4题 。(1)你发现了什么规律?用含有字母的式子表示出来。正方形的个数为n时,所需小棒的根数为1+3n。(2)如果摆100个正方形,需要多少根小棒? 当n=100时,1+3n的值是301,即摆100个正方形,需要301根小棒。8.猜一猜。 教材第81页“巩固与应用”第8题 。解:设这个数为x。
5x+5=100
x=19
答:这个数是19。8.猜一猜。 教材第81页“巩固与应用”第8题 。解:设这个数是x。答:这个数是8。谈谈你的收获吧!1.用字母表示规律、公式的方法。
2.解方程的方法。
3. 用方程解决简单的实际问题。3. 教材第81页“巩固与应用”第3题 。左图中,圆的半径是r,请你用含有字母的式子表示出正方形的周长和面积。周长:8r面积:4r215x=60x+2x=12.6解:x=60÷15x=4解:3x=12.6x=12.6÷3x=4.240%x=4.2解:x=4.2÷40%x=10.55.解方程。 教材第81页“巩固与应用”第5题 。5.解方程。 教材第81页“巩固与应用”第5题 。12+x=252x÷5=15解:x=25-12x=13解:2x=15×5x=75÷2x=37.54x-1.6x=36解:2.4x=36x=157.每种丛书有多少本? 教材第81页“巩固与应用”第7题 。解:设每种丛书有x本。
8.2x+6.8x=120
x=8
答:每种丛书有8本。一、想一想,填一填1.甲数是a,比乙数少2,乙数是( )。a+22.工地有x(x>15)吨沙子,每天用2.5吨,用了6天后
还剩( )吨。x-153.某路公交车上原有y人,在某站点下车6人,上来
15人,车上现有( )人。y+94.张老师买了3个足球,每个足球x元,他付给售货
员300元,那么3x表示( ),
300-3x表示( )。买3个足球共用去的钱数应该找回的钱数5.一个边长为a分米的正方形,边长增加1分米后,
面积可增加( )平方分米。2a+16.在三角形中,如果用S表示面积,a表示底,h表示
底边上的高,用字母表示求高的公式:
h=( )。2S÷a7.用x与y的和除以它们的差,列式为
( )。(x与y不相等)(x+y)÷(x-y)8.在一列数1,4,7,10,13……中,第n个数用式子表
示为( )。3n-29.三个连续自然数,中间数是a,其他两个数分别
是( )和( )。a-1a+110.小明今年比妈妈小a岁,3年后,小明比妈妈小
( )岁。a二、我是聪明的小法官1.4x+84是方程。 ( )
2.10x=0,这个方程没有解。 ( )
3.5(a+3)=5a+3。 ( )
4.当a=2时,a·a=2a。 ( )×××√三、用线把下面各方程和它的解连接起来x+12=40 x=52
84-x=32 x=28
x÷14=5 x=0.5
2x+9=10 x=10
2(x-4)=12 x=2.25
12x-4x=10+8 x=70四、解方程解:解:解:解:五、选择题(将正确答案的序号填在括号里)1.下面的式子中,是方程的是( )。
A.3x+15 B.8-x>6 C.2x=18+92C2.一个两位数,它的十位数字是9,个位上的数
字是a,表示这个两位数的式子是( )。
A.9+a B.9a C.9×10+aC3.水果超市运进苹果m kg,比梨的2倍多n kg,求
运进梨的千克数的算式是( )。
A.m÷2-n
B.(m-n)÷2
C.(m+n)÷2B六、解决问题1.徒弟每天做a个零件,师傅每天做的零件数比
徒弟每天做的零件数的2倍少10个。(1)用式子表示师傅每天做的零件个数。(2a-10)个(2)用式子表示师徒二人合做一天做的零件个数。(3a-10)个2.学校买了2箱乒乓球,每箱25个,共花去25元,每
个乒乓球多少元?解:设每个乒乓球x元。
(25×2)×x=25
x=0.5
答:每个乒乓球0.5元。3.某食堂有煤14吨,烧了3个月后还剩2吨,这个食
堂平均每个月烧煤多少吨?解:设这个食堂平均每个月烧煤x吨。
3x+2=14
x=4
答:这个食堂平均每个月烧煤4吨。4.妈妈买了苹果和梨各2千克,共付10.4元,已知
梨每千克2.8元,则苹果每千克多少元?解:设苹果每千克x元。
2.8×2+2x=10.4
x=2.4
答:苹果每千克2.4元。5.一条公路,每天修75米,可20天修完。若想15天
修完这条公路,则平均每天要修多少米?解:设平均每天要修x米。
15x=75×20
x=100
答:平均每天要修100米。6.李明买了一件打八折的衣服,花了400元,这件
衣服的原价是多少元?解:设这件衣服的原价是x元。
80%x=400
x=500
答:这件衣服的原价是500元。7.修一条路,已经修了全长的 ,正好修了400米,
这条路全长多少米?解:设这条路全长x米。
x=2000
答:这条路全长2000米。
加法结合律:(a+b)+c=a+(b+c)
乘法交换律:a×b=b×a
乘法结合律:(a×b)×c=a×(b×c)
乘法分配律:(a+b)×c=a×c+b×c长方形的周长和面积公式:C=(a+b)×2 S=ab
正方形的周长和面积公式:C=4a S=a·a=a2
三角形的面积公式:S=ah÷2
平行四边形的面积公式:S=ah
梯形的面积公式:S=(a+b)h÷2
圆的周长和面积公式:C=πd或C=2πr S=πr2正方体的表面积和体积公式:
S=6a2 V=a·a·a=a3
长方体的体积公式:V=abh
圆柱的体积公式:V=Sh=πr2h
圆锥的体积公式:V= Sh= πr2h用字母表示数注意的问题:1.在含有字母的式子里,字母就读字母的名称,
字母与字母、字母与数字之间的乘号可以记
作“·”或省略不写。但要注意,在省略乘号
的时候,应当把数字写在字母的前面。
例如:a×4=4·a(或4a),n×m=n·m(或nm),
5×b×c=5·b·c(或5bc)。用字母表示数注意的问题:2.用字母表示除法、分数和比时,表示除数、分
母及比的后项的字母不能为0。3.用字母表示运算结果时,必须是最简单的式子。例1 如果速度用v表示、时间用t表示、路程用s表示,请你用字母表示它们之间的关系。S=vt练习一个长方形,它的长是宽的4倍。(1)如果宽是a厘米,那么长方形的周长是多少?周长:2×(4a+a)=10a(厘米)(2)在第(1)问的情况下,如果a=5,那么长方形的周
长和面积各是多少?周长:10a=10×5=50(厘米)面积:20×5=100(平方厘米)表示相等关系的式子叫等式。 等式的性质:等式两边同时加上或减去相同的一个数,等式仍然成立。等式的两边同时乘或除以相同的一个数(0除外),等式仍然成立。含有未知数的等式叫作方程。 使方程左右两边相等的未知数的值叫作方程的解。求方程的解的过程叫解方程。3.解下面的方程,并说一说你是怎么解的。9x-1.8=5.40.8x+1.2x=25解:9x=5.4+1.89x=7.2x=7.2÷9x=0.8解:2x=25x=25÷2x=12.5 方法1:直接根据四则运算中已知数与得数之间的关系,求未知数的值。 方法2:根据等式的性质计算。例2解方程:60%x-2×4=10.6。解法一解: 60%x-8=10.6
60%x=10.6+8
60%x=18.6
x=18.6÷0.6
x=31例2解方程:60%x-2×4=10.6。解法二解: 60%x-8=10.6
60%x-8+8=10.6+8,
60%x=10.6+8
60%x=18.6
60%x÷60%=18.6÷60%
x=18.6÷0.6
x=31练习解方程0.6x-2×4=52。解: 0.6x-8+8=52+8
0.6x=60
0.6x÷0.6=60÷0.6
x=1004.列方程解决下列问题。(1)果品商店购进20箱苹果,购进苹果的箱数是
橘子箱数的 。商店购进了多少箱橘子?解:设商店购进了x箱橘子。答:商店购进了25箱橘子。(2)妙想、乐乐各收集了多少枚邮票?解:设乐乐收集了x枚邮票。
x+3x=128
x=3232×3=96(枚)答:妙想收集了96枚,乐乐收集了32枚。(3)淘气家和奇思家相距1240 m。一天,两人约
定在两家之间的路上回合。淘气每分走75 m,
奇思每分走80 m。两人同时从家出发,多长
时间后能相遇?解:设x分后能相遇。
75x+80x=1240
x=8答:8分后能相遇。例3 笑笑到文具店去买铅笔。如果买5支,还剩0.3元;如果买6支,则差0.2元。笑笑带了多少元钱?解:设每支铅笔的价钱为x元。
5x+0.3=6x-0.2
x=0.5
5×0.5+0.3=2.8(元)或6×0.5-0.2=2.8(元)
答:笑笑带了2.8元钱。 利民超市原来有一些饺子粉,每袋5千克,卖出7袋以后,还剩40千克。这个超市原来有多少千克饺子粉?(用方程解)解:设这个超市原来有x千克饺子粉。
x-5×7=40
x-35+35=40+35
x=75
答:这个超市原来有75千克饺子粉。列方程解应用题的一般步骤:1.分析题意,明确题中的数量关系。2.用字母(x或y)表示题中的未知数。设未知数的
方法有两种:一种是直接设定,即题中求什么就
设什么;二是间接设定,先设某一个数为x后,通
过这个数去求所求的未知数。列方程解应用题的一般步骤:3.找出题中数量间的等量关系,并根据等量关系
列方程。4.解方程,求出未知数的值。5.可以检验,之后写出答语。1.填一填。 教材第81页“巩固与应用”第1题 。(1)比x少25的数是 。(2)n的5倍与m的差是 。(3)一件衬衫a元,一件毛衣的价格比它的2倍
还多6元,毛衣的价格是 元。(4)原价a元的产品打八折后的价钱是 元。x-255n-m2a+680%a4.摆正方形。 教材第81页“巩固与应用”第4题 。(1)你发现了什么规律?用含有字母的式子表示出来。正方形的个数为n时,所需小棒的根数为1+3n。(2)如果摆100个正方形,需要多少根小棒? 当n=100时,1+3n的值是301,即摆100个正方形,需要301根小棒。8.猜一猜。 教材第81页“巩固与应用”第8题 。解:设这个数为x。
5x+5=100
x=19
答:这个数是19。8.猜一猜。 教材第81页“巩固与应用”第8题 。解:设这个数是x。答:这个数是8。谈谈你的收获吧!1.用字母表示规律、公式的方法。
2.解方程的方法。
3. 用方程解决简单的实际问题。3. 教材第81页“巩固与应用”第3题 。左图中,圆的半径是r,请你用含有字母的式子表示出正方形的周长和面积。周长:8r面积:4r215x=60x+2x=12.6解:x=60÷15x=4解:3x=12.6x=12.6÷3x=4.240%x=4.2解:x=4.2÷40%x=10.55.解方程。 教材第81页“巩固与应用”第5题 。5.解方程。 教材第81页“巩固与应用”第5题 。12+x=252x÷5=15解:x=25-12x=13解:2x=15×5x=75÷2x=37.54x-1.6x=36解:2.4x=36x=157.每种丛书有多少本? 教材第81页“巩固与应用”第7题 。解:设每种丛书有x本。
8.2x+6.8x=120
x=8
答:每种丛书有8本。一、想一想,填一填1.甲数是a,比乙数少2,乙数是( )。a+22.工地有x(x>15)吨沙子,每天用2.5吨,用了6天后
还剩( )吨。x-153.某路公交车上原有y人,在某站点下车6人,上来
15人,车上现有( )人。y+94.张老师买了3个足球,每个足球x元,他付给售货
员300元,那么3x表示( ),
300-3x表示( )。买3个足球共用去的钱数应该找回的钱数5.一个边长为a分米的正方形,边长增加1分米后,
面积可增加( )平方分米。2a+16.在三角形中,如果用S表示面积,a表示底,h表示
底边上的高,用字母表示求高的公式:
h=( )。2S÷a7.用x与y的和除以它们的差,列式为
( )。(x与y不相等)(x+y)÷(x-y)8.在一列数1,4,7,10,13……中,第n个数用式子表
示为( )。3n-29.三个连续自然数,中间数是a,其他两个数分别
是( )和( )。a-1a+110.小明今年比妈妈小a岁,3年后,小明比妈妈小
( )岁。a二、我是聪明的小法官1.4x+84是方程。 ( )
2.10x=0,这个方程没有解。 ( )
3.5(a+3)=5a+3。 ( )
4.当a=2时,a·a=2a。 ( )×××√三、用线把下面各方程和它的解连接起来x+12=40 x=52
84-x=32 x=28
x÷14=5 x=0.5
2x+9=10 x=10
2(x-4)=12 x=2.25
12x-4x=10+8 x=70四、解方程解:解:解:解:五、选择题(将正确答案的序号填在括号里)1.下面的式子中,是方程的是( )。
A.3x+15 B.8-x>6 C.2x=18+92C2.一个两位数,它的十位数字是9,个位上的数
字是a,表示这个两位数的式子是( )。
A.9+a B.9a C.9×10+aC3.水果超市运进苹果m kg,比梨的2倍多n kg,求
运进梨的千克数的算式是( )。
A.m÷2-n
B.(m-n)÷2
C.(m+n)÷2B六、解决问题1.徒弟每天做a个零件,师傅每天做的零件数比
徒弟每天做的零件数的2倍少10个。(1)用式子表示师傅每天做的零件个数。(2a-10)个(2)用式子表示师徒二人合做一天做的零件个数。(3a-10)个2.学校买了2箱乒乓球,每箱25个,共花去25元,每
个乒乓球多少元?解:设每个乒乓球x元。
(25×2)×x=25
x=0.5
答:每个乒乓球0.5元。3.某食堂有煤14吨,烧了3个月后还剩2吨,这个食
堂平均每个月烧煤多少吨?解:设这个食堂平均每个月烧煤x吨。
3x+2=14
x=4
答:这个食堂平均每个月烧煤4吨。4.妈妈买了苹果和梨各2千克,共付10.4元,已知
梨每千克2.8元,则苹果每千克多少元?解:设苹果每千克x元。
2.8×2+2x=10.4
x=2.4
答:苹果每千克2.4元。5.一条公路,每天修75米,可20天修完。若想15天
修完这条公路,则平均每天要修多少米?解:设平均每天要修x米。
15x=75×20
x=100
答:平均每天要修100米。6.李明买了一件打八折的衣服,花了400元,这件
衣服的原价是多少元?解:设这件衣服的原价是x元。
80%x=400
x=500
答:这件衣服的原价是500元。7.修一条路,已经修了全长的 ,正好修了400米,
这条路全长多少米?解:设这条路全长x米。
x=2000
答:这条路全长2000米。
