1.2 矩形的性质与判定（3）同步作业

21世纪教育网 –中小学教育资源及组卷应用平台
1.2 矩形的性质与判定（3）同步作业
姓名：___________班级：___________考号：___________
一、选择题
1．如图，在矩形ABCD中，对角线相交于点，则AB的长是（ ）
A. 3cm B. 6cm C. 10cm D. 12cm
2．如图，点O是矩形ABCD的对角线AC的中点，OM//AB交AD于点M，若OM=3，BC=10，则OB的长为（ ）
A. 5 B. 4 C. D.
3．如图，将长方形ABCD沿直线BD折叠，使点C落在点E处，BE交AD于F，连接CE，下列结论①FA=FE ②BD平分∠FBC ③∠DEC=∠EBD ④EC垂直平分BD，正确的是（　　）
A. ①② B. ①②③ C. ②③④ D. ①②③④
4．如图，在矩形ABCD中，AB＝2，BC＝3，M为BC中点，连接AM，过D作DE⊥AM于E，则DE的长度为( )
A. 2 B. EMBED Equation.DSMT4 C. 3 D.
5．如图，E、F分别是矩形ABCD的边AD、AB上的点，若EF=EC，EF⊥EC，DC= EMBED Equation.DSMT4 ，则BE的长为（　　）
A. B. C. 4 D. 2
6．如图，矩形ABCD的两条对角线相交于点O，∠AOB＝120°，AD＝2，点E是BC的中点，连结OE，则OE的长是（ ）
A. B. 2 C. 2 D. 4
7．如图，△ABC中，∠ABC＝∠BAC，D是AB的中点，EC∥AB，DE∥BC，AC与DE交于点O．下列结论中，不一定成立的是（　　）
A. AC＝DE B. AB＝AC C. AD＝EC D. OA＝OE
8．如图，E是矩形ABCD内的一个动点，连接EA、EB、EC、ED，得到△EAB、△EBC、△ECD、△EDA，设它们的面积分别是m、n、p、q，给出如下结论：①m+n=q+p；②m+p=n+q；③若m=n，则E点一定是AC与BD的交点；④若m=n，则E点一定在BD上．其中正确结论的序号是（　　）
A. ①③ B. ②④ C. ①②③ D. ②③④
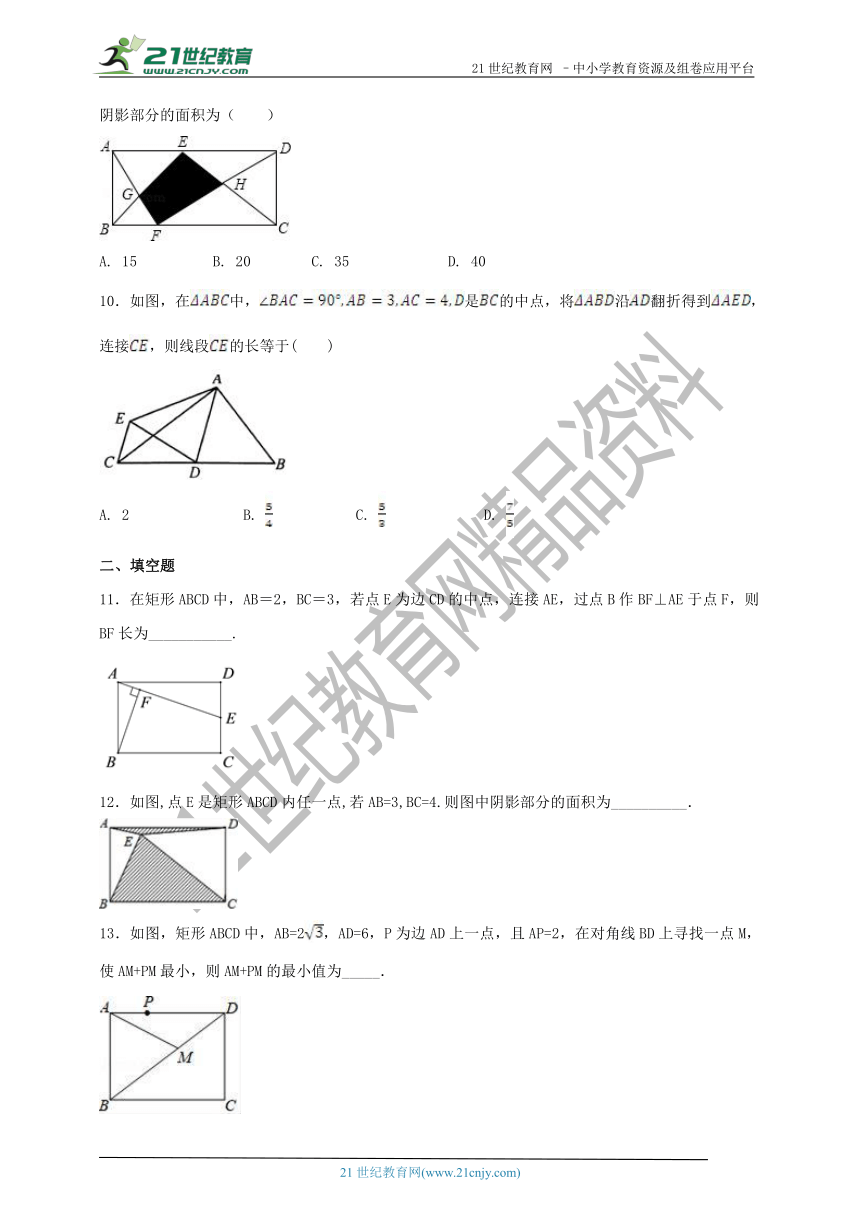
9．如图，E，F分别是矩形ABCD边AD、BC上的点，且△ABG，△DCH的面积分别为15和20，则图中阴影部分的面积为（　　）
A. 15 B. 20 C. 35 D. 40
10．如图，在中，是的中点，将沿翻折得到，连接，则线段的长等于( )
A. 2 B. C. D.
二、填空题
11．在矩形ABCD中，AB＝2，BC＝3，若点E为边CD的中点，连接AE，过点B作BF⊥AE于点F，则BF长为___________.
12．如图,点E是矩形ABCD内任一点,若AB=3,BC=4.则图中阴影部分的面积为__________．
13．如图，矩形ABCD中，AB=2，AD=6，P为边AD上一点，且AP=2，在对角线BD上寻找一点M，使AM+PM最小，则AM+PM的最小值为_____．
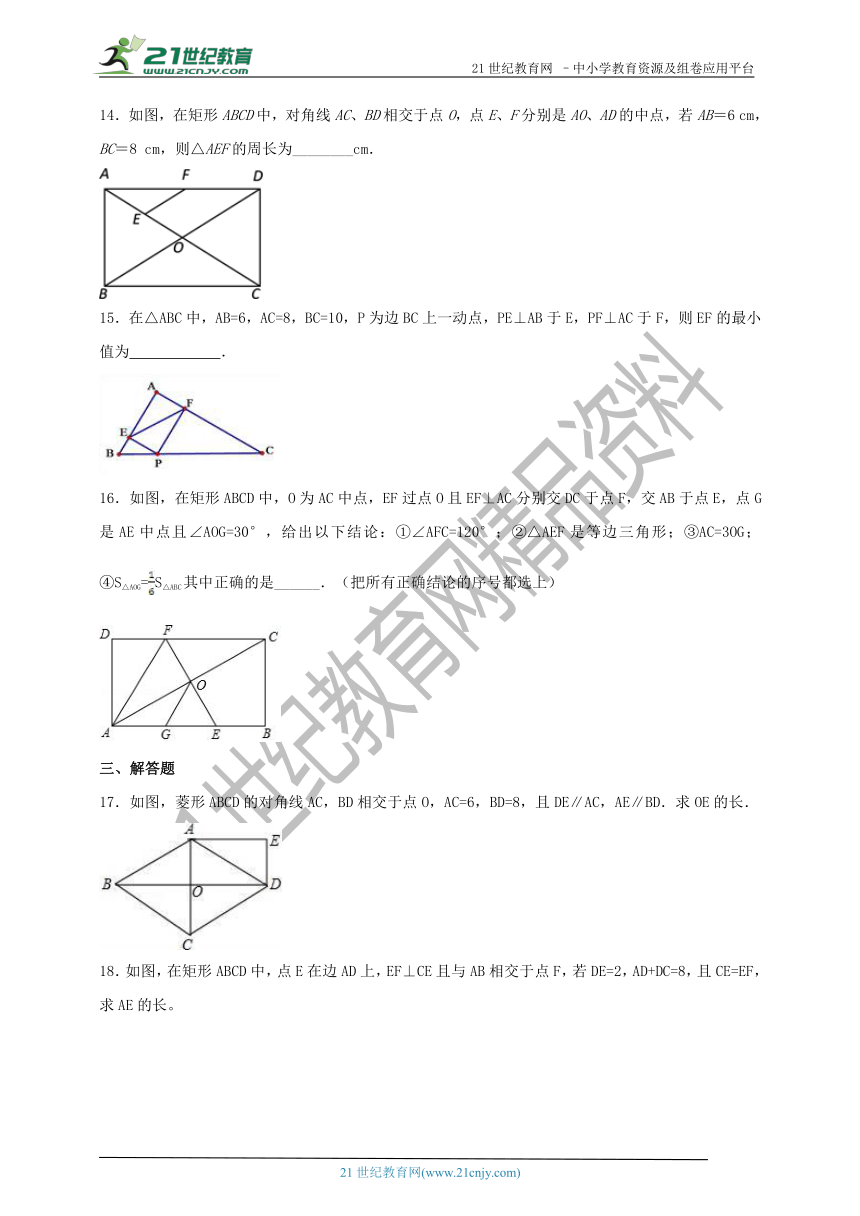
14．如图，在矩形ABCD中，对角线AC、BD相交于点O，点E、F分别是AO、AD的中点，若AB＝6 cm，BC＝8 cm，则△AEF的周长为________cm．
15．在△ABC中，AB=6，AC=8，BC=10，P为边BC上一动点，PE⊥AB于E，PF⊥AC于F，则EF的最小值为　　　　　　．
16．如图，在矩形ABCD中，O为AC中点，EF过点O且EF⊥AC分别交DC于点F，交AB于点E，点G是AE中点且∠AOG=30°，给出以下结论：①∠AFC=120°；②△AEF是等边三角形；③AC=3OG；④S△AOG=S△ABC其中正确的是______．（把所有正确结论的序号都选上）
三、解答题
17．如图，菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，且DE∥AC，AE∥BD．求OE的长．
18．如图，在矩形ABCD中，点E在边AD上，EF⊥CE且与AB相交于点F，若DE=2，AD+DC=8，且CE=EF，求AE的长。
19．如图，在矩形ABCD中，M，N分别是AD，BC的中点，E，F分别是线段BM，CM的中点，若AB=8，AD=12，则四边形ENFM的周长是多少？
20．如图，已知□ABCD，延长AB到E使BE=AB，连接BD，ED，EC，若ED=AD．
（1）求证：四边形BECD是矩形；
（2）连接AC，若AD=4，CD= 2，求AC的长．
21．如图，在四边形ABCD中，AD∥BC，∠ABC=∠ADC=90°，对角线AC，BD交于点O，DE平分∠ADC交BC于点E，连接OE．
（1）求证：四边形ABCD是矩形；
（2）若AB=2，求△OEC的面积．
22．如图，等腰△ABC中，AB＝AC，BD，CE分别是边AC，AB上的中线，BD与CE相交于点O，点M，N分别为线段BO和CO的中点．求证：四边形EDNM是矩形．
参考答案
1．A
【解析】试题解析：∵四边形ABCD是矩形，
∴OA=OC=OB=OD=3，
∴△AOB是等边三角形，
∴AB=OA=3，
故选A.
点睛：有一个角等于得等腰三角形是等边三角形.
2．D
【解析】分析：在Rt△AOM中，用勾股定理求AO，根据BO是Rt△ABC斜边上的中线求解.
详解：因为四边形ABCD是矩形，所以AD＝BC＝10，∠ABC＝∠D＝90°.
因为OM∥AB，所以∠AMO＝∠D＝90°.
因为OM＝3，AM＝AD＝×10＝5.
Rt△AMO中，由勾股定理得AO＝.
因为O是矩形ABCD的对角线AC的中点，
所以OB＝AO＝.
故选D.
点睛：本题考查了勾股定理和矩形的性质及直角三角形斜边上的中线,矩形的对边相等，四个角都是直角，直角三角形斜边上的中线等于斜边的一半.
3．B
【解析】试题解析：由折叠的性质可知，DE=DC，∠BED=∠BCD=90°，
在△ABF和△EDF中，
，
∴△ABF≌△EDF，
∴FA=FE，①正确；
由折叠的性质可知，∠EBD=∠CBD，
∴BD平分∠FBC，②正确；
∵∠BED=∠BCD=90°，
∴E、B、C、D四点共圆，又DE=DC，
∴∠DEC=∠EBD，③正确；
由折叠的性质可知，BD垂直平分EC，④错误，
故选B．
4．B
【解析】连接DM，
则△ADM的面积为3，根据中点的性质可得：BM=1.5，在Rt△ABM中，根据勾股定理可得：AM=2.5，则根据等面积法可得：DE=3×2÷2.5=.
故选B.
5．D
【解析】根据矩形的性质和已知条件，由全等三角形的判定AAS，可证明△AEF≌△DCE；根据全等三角形的的性质，可知AE=DC=，在Rt△ABE中由勾股定理可求得BE=2．
故选：D.
6．A
【解析】试题解析：∵四边形ABCD 是矩形，
∴AC=BD，OA=OB，∠DAB=90°
∵∠AOB＝120°
∴∠BAO＝30°
在RtΔABD中，BD=2AD=4
∴AB=
∵点E是CB的中点，
∴OE是△ACD的中位线，
∴OE=AB=．
故选A.
7．B
【解析】A.连接AE，CD，则四边形ADCE是平行四边形，因为∠ABC＝∠BAC，D是AB的中点，所以CD⊥AB，所以四边形ADCE是矩形，所以AC=DE，则A成立；B.因为∠ABC＝∠BAC，D是AB的中点，所以CA=CB，不能得到AB=AC，则B不一定成立；C.因为四边形ADCE是矩形，所以AD=CE，OA=OE，则C，D成立，故选B.
8．B
【解析】分析：过E作MN⊥AB，交AB于M，CD于N，作GH⊥AD，交AD于G，BC于H，由矩形的性质容易证出①不正确，②正确；若m=n，则p=q，作AP⊥BE于P，作CQ⊥DE于Q，延长BE交CD于F，先证AP=CQ，再证明△ABP≌△CFQ，得出AB=CF，F与D重合，得出③不正确，④正确，即可得出结论．
详解：过E作MN⊥AB，交AB于M，CD于N，作GH⊥AD，交AD于G，BC于H，如图1所示： 则m=AB EM，n=BC EH，p=CD EN，q=AD EG，
∵四边形ABCD是矩形， ∴AB=CD=GH，BC=AD=MN，
∴m+p=AB MN=AB BC，n+q=BC GH=BC AB， ∴m+p=n+q；∴①不正确，②正确；
若m=n，则p=q，作AP⊥BE于P，作CQ⊥BE于Q，延长BE交CD于F，如图2所示：
则∠APB=∠CQF=90°， ∵m=BE AP，n=BE CQ， ∵m=n， ∴AP=CQ，
∵AB∥CD， ∴∠1=∠2， ∴△ABP≌△CFQ（AAS）， ∴AB=CF， ∴F与D重合，
∴E一定在BD上； ∴③不正确，④正确． 故选：B．
点睛：本题考查了矩形的性质、三角形面积的计算、全等三角形的判定与性质；熟练掌握矩形的性质，证明三角形全等是解决问题的关键．
9．C
【解析】试题解析：连接EF，由图可知 ，那么 ，
所以 ，同理， ，则,
故本题应选C.
10．D
【解析】分析：连接BE交AD于O，作AH⊥BC于H．首先证明AD垂直平分线段BE，△BCE是直角三角形，求出BC、BE，在Rt△BCE中，利用勾股定理即可解决问题．
详解： 如图连接BE交AD于O，作AH⊥BC于H．
在Rt△ABC中，∵AC=4，AB=3，
∴BC==5，
∵CD=DB，
∴AD=DC=DB=，
∵ BC AH= AB AC，
∴AH=，
∵AE=AB，DE=DB=DC，
∴AD垂直平分线段BE，△BCE是直角三角形，
∵ AD BO= BD AH，
∴OB=，
∴BE=2OB=，
在Rt△BCE中，EC=，
故选：D．
点睛：本题考查翻折变换、直角三角形的斜边中线的性质、勾股定理等知识，解题的关键是学会利用面积法求高，属于中考常考题型．
11．
【解析】分析：根据S△ABE=S矩形ABCD=3= AE BF，先求出AE，再求出BF即可．
详解：如图，连接BE．
∵四边形ABCD是矩形，
∴AB=CD=2，BC=AD=3，∠D=90°，
在Rt△ADE中，AE=，
∵S△ABE=S矩形ABCD=3= AE BF，
∴BF=．
故答案为．
点睛：本题考查矩形的性质、勾股定理、三角形的面积公式等知识，解题的关键是灵活运用所学知识解决问题，学会用面积法解决有关线段问题，
12．6
【解析】试题解析：∵四边形ABCD是矩形，
∴AD=BC=4，
设两个阴影部分三角形的底为AD，BC，高分别为h1，h2，则h1+h2=AB，
∴S△EAB+S△ECD=AD h1+BC h2=AD（h1+h2）=AD AB=矩形ABCD的面积=×3×4=6；
故答案为：6．
13．2
【解析】分析：作DH平分∠BDC交BC于H．连接AH交BD于M．首先证明P、H关于BD对称,连接AH交BD于M,则AM+PM的值最小,最小值=AH.
详解：作DH平分∠BDC交BC于H．连接AH交BD于M．
∵四边形ABCD是矩形，
∴∠C=∠BAD=∠ADC=90°，
∴tan∠ADB=，
∴∠ADB=30°，
∴∠BDC=60°，
∴∠CDH=30°，
∵CD= AB=2，
∴CH= tan30 ×22，
∴DH=2CH=4，
∴DP=DH，
∵∠MDP=∠MDH，
∴P、H关于BD对称，连接AH交BD于M，则AM+PM的值最小，最小值=AH=．
点睛：本题考查了矩形的性质，解直角三角形，勾股定理，含30 角的直角三角形的性质，轴对称的性质，作DH平分∠BDC交BC于H．连接AH交BD于M．说明P和H关于BD成轴对称是解答本题的关键.
14．9
【解析】利用勾股定理求出AC，再根据矩形的对角线互相平分且相等求出OA=OD=AC，然后根据三角形的中位线平行于第三边并且等于第三边的一半可得EF=OD，再求出AF，AE，然后根据三角形的周长公式列式计算即可得解．
解：由勾股定理得，AC===10cm，
∵四边形ABCD是矩形，
∴OA=OD=AC=×10=5cm，
∵点E、F分别是AO、AD的中点，
∴EF=OD=cm，
AF=×8=4cm，
AE=OA=cm，
∴△AEF的周长=+4+=9cm.
故答案为：9.
15．4.8
【解析】试题解析：∵AB=6cm，AC=8cm，BC=10cm，
∴AB2+AC2=BC2，
∴△ABC为直角三角形，∠A=90°，
∵PE⊥AB于E，PF⊥AC于F，
∴∠AEP=∠AFP=90°，
∴四边形AEPF为矩形，
连接AP，如图，EF=AP，当AP的值最小时，EF的值最小，
当AP⊥BC时，AP的值最，此时AP=，
∴EF的最小值为．
故答案为4.8．
点睛：此题考查了矩形的判定与性质：关于矩形，应从平行四边形的内角的变化上认识其特殊性：一个内角是直角的平行四边形，进一步研究其特有的性质：是轴对称图形、内角都是直角、对角线相等．同时平行四边形的性质矩形也都具有．在处理许多几何问题中，若能灵活运用矩形的这些性质，则可以简捷地解决与角、线段等有关的问题．
16．①②④．
【解析】试题分析：根据直角三角形斜边上的中线等于斜边的一半可得OG=AG=GE=AE，再根据等边对等角可得∠OAG=30°，∠EOG=60°，从而根据矩形的性质得到∠ACF=30°，因此由线段垂直平分线的性质可得FC=AF，因此可根据等边对等角得到∠FAE=30°，根据三角形的内角和求得∠AFC=120°，故①正确；
由∠AFC=120°，∠FCA=30°，可知∠AFE=60°，因此△AEF是等边三角形，故②正确；
连接CE，则根据三角形的中位线可知CE=2OG，由矩形的性质可得四边形AECF是菱形，且，由OE=OG，OA=AC，可知，解得AC=OG，故③不正确；
令AE=2a，则OG=OE=a，AO=a，AC=2a，由S△AOE=×a×a=2，S矩形ABCD=3a×a=3a2 ，即S△AOG＝S△ABC，故④正确.
故答案为：①②④.
17．5
【解析】试题分析：根据菱形的性质得出AC⊥BD,再根据平行四边形的判定定理得四边形AODE为平行四边形,由矩形的判定定理得出四边形AODE是矩形,则该矩形的对角线相等,即AD=OE.
解：∵四边形ABCD为菱形，
∴AC⊥BD，OA=AC=3，OD=BD=4，
∴∠AOD=90°，
∴AD===5．
∵DE∥AC，AE∥BD，
∴四边形AODE为平行四边形，
∴四边形AODE是矩形，
∴OE=AD=5．
点睛：本题考查了矩形的判定及性质，及菱形的性质，勾股定理的应用，熟练掌握平行菱形的性质和矩形的判定方法是解题的关键．
18．AE=3
【解析】试题分析：先利用AAS证明 EMBED Equation.DSMT4 ,得到AE=CD,可求AE值.
试题解析：
∠AEF+∠DEC=90°，∠DCE+∠DEC=90°，
∠AEF=∠DCE， CE=EF,∠EAF=∠EDC,
,
CD=EA,
DE=2，AD+DC=8,DE+2AE=8，
AE=3.
19．20
【解析】分析：根据M是边AD的中点，得AM=DM=6，根据勾股定理得出BM=CM=10，再根据E、F分别是线段BM、CM的中点，即可得出EM=FM=5，再根据N是边BC的中点，得出EM=FN，EN=FM，从而得出四边形ENFM的周长．
详解：∵M、N分别是边AD、BC的中点，AB=8，AD=12，
∴AM=DM=6，
∵四边形ABCD为矩形，
∴∠A=∠D=90°，
∴BM=CM=10，
∵E、F分别是线段BM、CM的中点，
∴EM=FM=5，
∴EN，FN都是△BCM的中位线，
∴EN=FN=5，
∴四边形ENFM的周长为5+5+5+5=20．
20．（1）证明见解析；（2）
【解析】分析：
（1）由已知条件易得四边形BECD是平行四边形及AD=BC，结合ED=AD可得BC=ED，由此可得平行四边形BECD是矩形；
（2）如下图，连接AC，由已知条件和（1）中结论易得BC=AD=4，BE=CD=AB=2，∠AEC=90°，由此在Rt△BCE中，可得CE=，这样在Rt△ACE中，由勾股定理可得AC=.
详解：
（1）∵四边形ABCD是平行四边形，
∴AB∥CD，AB=CD．
∵BE=AB，
∴BE=CD．
∴四边形BECD是平行四边形．
∵AD=BC，AD =DE，
∴BC=DE．
∴平行四边形BECD是矩形．
（2）如下图，连接AC，
∵AD=4，CD=2，四边形ABCD是平行四边形，四边形BECD是矩形，
∴AB=BE=CD=2,BC=AD=4，∠AEC=90°，
∴AE=AB+BE=4，在Rt△BCE中，CE=，
∴在Rt△ACE中，AC=.
点睛：熟悉“平行四边形的性质与判定和矩形的判定方法”是正确解答本题的关键.
21．（1）证明见解析；（2）1.
【解析】分析：（1）只要证明三个角是直角即可解决问题；
（2）作OF⊥BC于F．求出EC、OF的长即可；
详解：（1）证明：∵AD∥BC，
∴∠ABC+∠BAD=180°，
∵∠ABC=90°，
∴∠BAD=90°，
∴∠BAD=∠ABC=∠ADC=90°，
∴四边形ABCD是矩形．
（2）作OF⊥BC于F．
∵四边形ABCD是矩形，
∴CD=AB=2，∠BCD=90°，AO=CO，BO=DO，AC=BD，
∴AO=BO=CO=DO，
∴BF=FC，
∴OF=CD=1，
∵DE平分∠ADC，∠ADC=90°，
∴∠EDC=45°，
在Rt△EDC中，EC=CD=2，
∴△OEC的面积= EC OF=1．
点睛：本题考查矩形的判定和性质、角平分线的定义、三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题
22．见解析
【解析】试题分析：由题意得出ED是△ABC的中位线，得出ED∥BC，ED=BC，由题意得出MN是△OBC的中位线，得出MN∥BC，MN=BC，因此ED∥MN，ED=MN，证明四边形EDNM是平行四边形，再由SAS证明△ABD≌△ACE，得出BD=CE，证出DM=EN，即可得出四边形EDNM是矩形．
试题解析：证明：∵BD，CE分别是AC，AB边上的中线
∴AE＝AB，AD＝AC，ED是△ABC的中位线
∴ED∥BC，ED＝BC.
∵点M，N分别为线段BO和CO的中点
∴OM＝BM，ON＝CN，MN是△OBC的中位线
∴MN∥BC，MN＝BC
∴ED∥MN，ED＝MN
∴四边形EDNM是平行四边形
∴OE＝ON，OD＝OM.∵AB＝AC
∴AE＝AD.
在△ABD和△ACE中，
∴△ABD≌△ACE
∴BD＝CE
∴EO＋ON＋CN＝BM＋OM＋OD
∴3OE＝3OM，
即OE＝OM.
又∵DM＝2OM，EN＝2OE，
∴DM＝EN
∴四边形EDNM是矩形
点睛：本题考查了等腰三角形的性质、三角形中位线定理、矩形的判定、平行四边形的判定与性质、全等三角形的判定与性质；熟练掌握等腰三角形的性质和三角形中位线定理，并能进行推理论证是解决问题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)