数学六年级下苏教版5大树有多高 (共15张)
文档属性
| 名称 | 数学六年级下苏教版5大树有多高 (共15张) |  | |
| 格式 | ppt | ||
| 文件大小 | 507.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-21 06:24:12 | ||
图片预览





文档简介
(共12张PPT)
苏教版六年级数学下册
有个好朋友,天天跟我走。
有时走在前,有时走在后。
我和他说话,就是不开口。
(谜底:影子)
你能举例说明影子的什么作用吗?
要知道一棵大树的高度,可以怎样做?
与同学交流一下。
太阳光下,把几根同样长的竹竿直立在地面上,同时量出每根竹竿的影长。
把几根长度不同的竹竿直立在地面上,同时量出每根竹竿的影长。
1 2 3 4 ……
竹竿长 ……
影 长 ……
竹竿长与影长的比值 ……
(1)按要求填表。
(2)计算竹竿与影长的比值。(得数保留两位小数)
(3)讨论:根据每次求得的比值,你有什么发现?
在同一地点同时测量不同的竹竿高度与影长的比值是相等的。
1 2 3 4 ……
竹竿长 ……
影 长 ……
竹竿长与影长的比值 ……
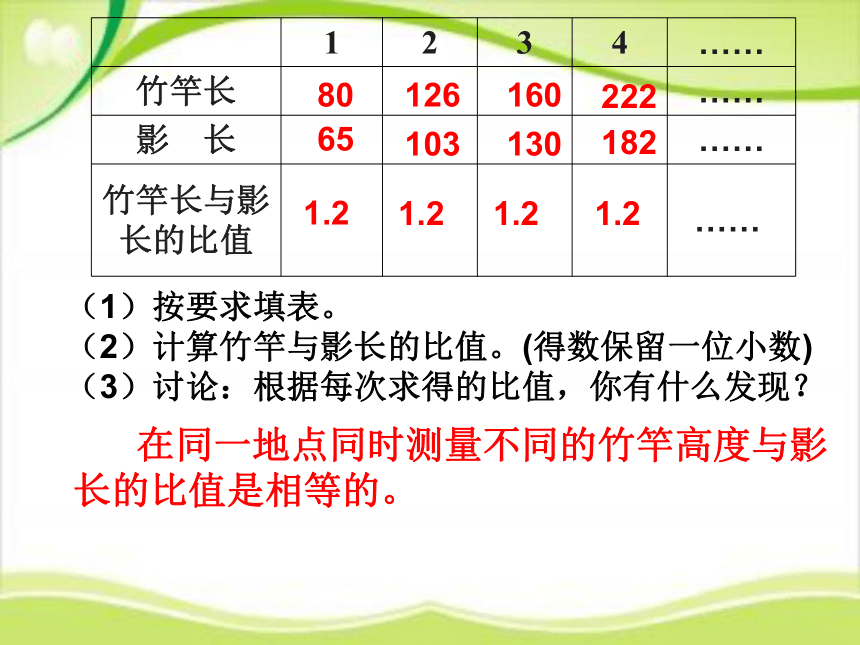
(1)按要求填表。
(2)计算竹竿与影长的比值。(得数保留一位小数)
(3)讨论:根据每次求得的比值,你有什么发现?
80
126
222
160
1.2
103
65
130
182
1.2
1.2
1.2
在同一地点同时测量物体高度与影长成正比例。
结论:
你能应用上面发现的规律,通过测量和计算求出大树的高度吗?
说说你的想法。
影长/cm 实际高度/cm
竹 竿
大 树
在太阳光下,先用一根竹竿的高度和影长及量出当时大树的影长,并把结果填在下表里。
根据表中的数据,可以怎样推算大树的高度?与同学交流你的想法
影长/cm 实际高度/cm
竹 竿
大 树
在太阳光下,先用一根竹竿的高度和影长及量
出当时大树的影长,并把结果填在下表里。
根据表中的数据,可以怎样推算大树的高度?(得数保留整数)与同学交流你的想法.
160
145
600
662
?
同一棵大树,在不同时间测量它的影长,结果相同吗?
通过上面的活动,你还能想到什么?
在同一时间、同一地点,物体的高度和影长成正比例。
同样高度的物体在不同的时间、不同的地点测出的影长是会变化的。
比较物体的高度和影长时,要在同一时间、同一地点进行。
1、 佳航在操场上插几根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长,情况如下表。
影长(米) 0.5 0.7 0.8 0.9 1.1 1.5
竹竿长(米) 1 1.4 1.6 1.8 2.2 3
这时,佳航身边的王强测量出了教学楼的影长
是6米,可推算出教学楼的实际高度是多少米?
2、 同学们测得旗杆的影长为21米,同时测得一旁直立的150厘米竹竿影长为225厘米,你能算出旗杆的实际高度吗?
苏教版六年级数学下册
有个好朋友,天天跟我走。
有时走在前,有时走在后。
我和他说话,就是不开口。
(谜底:影子)
你能举例说明影子的什么作用吗?
要知道一棵大树的高度,可以怎样做?
与同学交流一下。
太阳光下,把几根同样长的竹竿直立在地面上,同时量出每根竹竿的影长。
把几根长度不同的竹竿直立在地面上,同时量出每根竹竿的影长。
1 2 3 4 ……
竹竿长 ……
影 长 ……
竹竿长与影长的比值 ……
(1)按要求填表。
(2)计算竹竿与影长的比值。(得数保留两位小数)
(3)讨论:根据每次求得的比值,你有什么发现?
在同一地点同时测量不同的竹竿高度与影长的比值是相等的。
1 2 3 4 ……
竹竿长 ……
影 长 ……
竹竿长与影长的比值 ……
(1)按要求填表。
(2)计算竹竿与影长的比值。(得数保留一位小数)
(3)讨论:根据每次求得的比值,你有什么发现?
80
126
222
160
1.2
103
65
130
182
1.2
1.2
1.2
在同一地点同时测量物体高度与影长成正比例。
结论:
你能应用上面发现的规律,通过测量和计算求出大树的高度吗?
说说你的想法。
影长/cm 实际高度/cm
竹 竿
大 树
在太阳光下,先用一根竹竿的高度和影长及量出当时大树的影长,并把结果填在下表里。
根据表中的数据,可以怎样推算大树的高度?与同学交流你的想法
影长/cm 实际高度/cm
竹 竿
大 树
在太阳光下,先用一根竹竿的高度和影长及量
出当时大树的影长,并把结果填在下表里。
根据表中的数据,可以怎样推算大树的高度?(得数保留整数)与同学交流你的想法.
160
145
600
662
?
同一棵大树,在不同时间测量它的影长,结果相同吗?
通过上面的活动,你还能想到什么?
在同一时间、同一地点,物体的高度和影长成正比例。
同样高度的物体在不同的时间、不同的地点测出的影长是会变化的。
比较物体的高度和影长时,要在同一时间、同一地点进行。
1、 佳航在操场上插几根长短不同的竹竿,在同一时间里测量竹竿长和相应的影长,情况如下表。
影长(米) 0.5 0.7 0.8 0.9 1.1 1.5
竹竿长(米) 1 1.4 1.6 1.8 2.2 3
这时,佳航身边的王强测量出了教学楼的影长
是6米,可推算出教学楼的实际高度是多少米?
2、 同学们测得旗杆的影长为21米,同时测得一旁直立的150厘米竹竿影长为225厘米,你能算出旗杆的实际高度吗?
