数学六年级下人教新课标3.2圆锥的体积课件(21张)
文档属性
| 名称 | 数学六年级下人教新课标3.2圆锥的体积课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-21 09:05:34 | ||
图片预览







文档简介
(共21张PPT)
第三单元 圆柱和圆锥
3.5 圆锥的体积
教材第33~36页
课题引入
小麦堆得像小山一样,小麦丰收了。张小虎和爷爷笑得合不拢嘴。这时,爷爷用竹棍量了量麦堆的高和底面的直径,出了个难题要考考小虎:你能算出这堆小麦大约有多少立方米吗?这下可难住了小虎,因为他只学了圆柱的体积计算,圆锥的体积怎么计算还没有学,怎么办?捏那个帮助下小虎吗?
教学新知
想一想:我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
教学新知
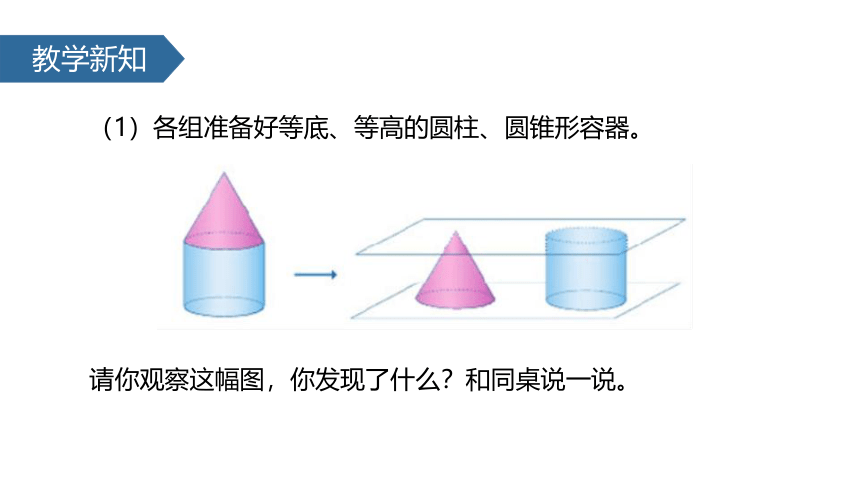
(1)各组准备好等底、等高的圆柱、圆锥形容器。
请你观察这幅图,你发现了什么?和同桌说一说。
教学新知
(2)用倒沙子或水的方法试一试。
知识要点
通过试验,我们发现圆锥的体积是与它等底、等高的圆柱的三分之一,所以:
V圆锥= V圆柱= sh= πr h
①沙堆底面积:
3.14×2 =3.14×4=12.56(㎡)
②沙堆的体积:
× 12.56×1.2=5.024≈5.02(m )
③沙堆的重量: 5.02×1.5=7.53(t)
答: 这吨沙子大约重7.53t 。
教学新知
试一试:工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的
体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重
多少吨?(得数保留两位小数。)
教学新知
做一做:
1.一个圆锥形的零件,底面积是19cm ,高是12cm。这个零件的体积
是多少?
V=
答:这个零件的体积是76cm 。
2.一个用钢铸造成的圆锥形铅锤,底面直径是4 cm, 高5 cm。每立方
厘米钢大约重7.8 g。这个铅锤重多少克?(得数保留整数。)
×3.14×2 ×5×7.8=163.28(克)
答:这个铅锤重163.28g。
教学新知
练一练:
1.一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4
dm,圆锥的高是多少?
2.一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是
28.26cm ,圆柱的底面积是多少?
4×3=12(dm)
答:圆锥的高是12dm。
28.26÷3=9.42(cm)
答:圆柱的底面积是9.42cm。
教学新知
例一:一个圆锥的底面积为6平方厘米,高为8厘米,这个圆锥的体积
是多少立方厘米?
【解析】根据圆锥的体积公式可以直接列式计算,6×8=48(立方厘米)。
【方法小结】求圆锥的体积就要找到圆锥的底面积和高,如果题中没有直接告诉底面积,就要通过找半径的方式求底面积再计算。
教学新知
例二:一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸完后沙堆成了一个高是5分米的圆锥形,它的底面积是多少平方米?
【解析】我们首先要清楚,这堆沙前后的体积是不变,要先用长方体的体积公式算出这些沙的体积,然后在根据圆锥体积公式的逆运算计算出底面积。当然根据前后体积不变的原理也可以列方程解决问题。参考答案为:4×1.5×4=24(立方米)
5分米=0.5米 24÷ ÷0.5=144(平方米)
课堂练习
1.判断。
(1)圆锥的体积等于圆柱体积的。 ( )
(2)两个体积相等、底面积相等的圆柱和圆锥,圆锥的高一定是圆
柱高的3倍。 ( )
(3)一个圆锥形物体,底面积是 a 平方米,高是 b 米,它的体积是
ab 立方米。 ( )
(4)把一根圆柱体木头,削成一个最大的圆锥体, 削去体积是圆锥
体积的2倍。 ( )
√
×
√
×
课堂练习
一、判断。
(5)圆柱体的体积一定比圆锥体的体积大。 ( )
(6)圆锥的体积等于和它等底等高圆柱体积的三分之一。 ( )
(7)正方体、长方体、圆柱体、圆锥体的体积都等于底面积×高。
( )
(8)一个圆柱的体积是27立方米,和它等底等高的圆锥的体积是9立
方米。 ( )
√
×
√
×
课堂练习
2.求下面圆锥的体积。(单位:dm)
V圆锥== sh= πr h= π×6 ×20=753.6(立方厘米)
课堂练习
3.一个圆锥的体积是32立方米,它的底面积为16平方米,那么这个圆
锥的高为多少米?
4.—个圆锥体和—个圆柱体的底面积和高都相等,它们的体积之和是
72立方厘米,这个圆锥体的体积是多少立方厘米?
3×32÷16=6(米)
答:这个圆锥的高为6米。
72÷(1+3)=18(立方厘米)
答:这个圆锥的体积为18立方厘米。
课堂练习
5.我班数学小组的同学利用课余时间测量了一堆沙子,得到了以下信
息:底面半径2米,底面直径4米,底面周长12.56米,底面积12.56平
方米,高1.2米,
(1)你能根据这些信息,用不同的方法计算出这堆沙子的体积吗?
(2)比较这些计算方法你发现了什么?
(3)准备把这堆沙填在一个长3.14米,宽2米的沙坑里,请同学们算
一算能填多深?
(1)略;(2)直接应用底面积乘高的方法最简便;
(3)12.56×1.2×÷(3.14×2)=0.8(米)
课后习题
1.填空题。
(1)圆锥的底面是个( );圆锥的侧面是一个( ),展开后
是一个( )。
(2)从圆锥的( )到( )的距离是圆锥的高。
(3)一个圆柱和一个圆锥等底等高时,圆锥的体积是圆柱的体积的
( );圆柱的体积是圆锥的体积的( ) 。
(4)圆柱的体积是18立方厘米,与它等底等高的圆锥的体积是
( )。
圆形
曲面
扇形
顶点
圆心
三倍
6立方厘米
课后习题
1.填空题。
(5)圆锥的体积是18立方厘米,与它等底等高的圆柱的体积是
( )。
(6)一个圆柱和一个圆锥等底等高,他们体积的和是48立方分米,
圆锥的体积是( )。
(7)一个圆柱和一个圆锥等底等高,圆柱的体积比圆锥的体积多7.8
立方米,圆柱的体积是( ),圆锥的体积是( )。
3.9立方米
11.7立方米
54立方厘米
12立方分米
2.求下面圆锥体的体积。
(1)底面积14.7平方厘米,高1分米。
(2)底面周长31.4米,高是3.9米。
(3)底面直径是4厘米,高是15厘米
课后习题
1分米=10厘米 ×14.7×10=49(立方厘米)
31.4÷3.14÷2=5(米) ×3.14×5 ×3.9=102.05(立方米)
×3.14×2 ×15=62.8(立方厘米)
课后习题
3.一个圆锥形沙堆,底面周长50.24米,高6米。这堆沙的体积是多少
立方米?
4.一个圆柱体,底面直径是8米,高是3米,求与它等底等高的圆锥体
的体积。
50.24÷3.14÷2=8(米) ×3.14×8 ×3=200.96(立方米)
答:这堆沙的体积是200.96立方米。
×3.14×4 ×3=50.24(立方米))
答:圆锥的体积是50.24立方米。
课后习题
5.将直角三角形ABC(如图),以AB为边为轴旋转一周,得到的圆锥体积
是V,那么V= 。
6.蒙古包也称“毡包”,是蒙古族传统民居,下图中的蒙古包是由一个
圆柱体和一个圆锥体组成的(单位:米)。这个蒙古包占地多少?内
部的空间约是多少?(得数保留整数。)
×3.14×4 ×3=50.24
50.24
3.14×4 =50.24(平方米)
×50.24×1.2+50.24×2=120.576
≈121(立方米)
第三单元 圆柱和圆锥
3.5 圆锥的体积
教材第33~36页
课题引入
小麦堆得像小山一样,小麦丰收了。张小虎和爷爷笑得合不拢嘴。这时,爷爷用竹棍量了量麦堆的高和底面的直径,出了个难题要考考小虎:你能算出这堆小麦大约有多少立方米吗?这下可难住了小虎,因为他只学了圆柱的体积计算,圆锥的体积怎么计算还没有学,怎么办?捏那个帮助下小虎吗?
教学新知
想一想:我们已经会计算圆柱的体积,如何计算圆锥的体积呢?
下面通过试验,探究一下圆锥和圆柱体积之间的关系。
教学新知
(1)各组准备好等底、等高的圆柱、圆锥形容器。
请你观察这幅图,你发现了什么?和同桌说一说。
教学新知
(2)用倒沙子或水的方法试一试。
知识要点
通过试验,我们发现圆锥的体积是与它等底、等高的圆柱的三分之一,所以:
V圆锥= V圆柱= sh= πr h
①沙堆底面积:
3.14×2 =3.14×4=12.56(㎡)
②沙堆的体积:
× 12.56×1.2=5.024≈5.02(m )
③沙堆的重量: 5.02×1.5=7.53(t)
答: 这吨沙子大约重7.53t 。
教学新知
试一试:工地上有一堆沙子,近似于一个圆锥(如下图)。这堆沙子的
体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重
多少吨?(得数保留两位小数。)
教学新知
做一做:
1.一个圆锥形的零件,底面积是19cm ,高是12cm。这个零件的体积
是多少?
V=
答:这个零件的体积是76cm 。
2.一个用钢铸造成的圆锥形铅锤,底面直径是4 cm, 高5 cm。每立方
厘米钢大约重7.8 g。这个铅锤重多少克?(得数保留整数。)
×3.14×2 ×5×7.8=163.28(克)
答:这个铅锤重163.28g。
教学新知
练一练:
1.一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4
dm,圆锥的高是多少?
2.一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是
28.26cm ,圆柱的底面积是多少?
4×3=12(dm)
答:圆锥的高是12dm。
28.26÷3=9.42(cm)
答:圆柱的底面积是9.42cm。
教学新知
例一:一个圆锥的底面积为6平方厘米,高为8厘米,这个圆锥的体积
是多少立方厘米?
【解析】根据圆锥的体积公式可以直接列式计算,6×8=48(立方厘米)。
【方法小结】求圆锥的体积就要找到圆锥的底面积和高,如果题中没有直接告诉底面积,就要通过找半径的方式求底面积再计算。
教学新知
例二:一辆货车箱是一个长方体,它的长是4米,宽是1.5米,高是4米,装满一车沙,卸完后沙堆成了一个高是5分米的圆锥形,它的底面积是多少平方米?
【解析】我们首先要清楚,这堆沙前后的体积是不变,要先用长方体的体积公式算出这些沙的体积,然后在根据圆锥体积公式的逆运算计算出底面积。当然根据前后体积不变的原理也可以列方程解决问题。参考答案为:4×1.5×4=24(立方米)
5分米=0.5米 24÷ ÷0.5=144(平方米)
课堂练习
1.判断。
(1)圆锥的体积等于圆柱体积的。 ( )
(2)两个体积相等、底面积相等的圆柱和圆锥,圆锥的高一定是圆
柱高的3倍。 ( )
(3)一个圆锥形物体,底面积是 a 平方米,高是 b 米,它的体积是
ab 立方米。 ( )
(4)把一根圆柱体木头,削成一个最大的圆锥体, 削去体积是圆锥
体积的2倍。 ( )
√
×
√
×
课堂练习
一、判断。
(5)圆柱体的体积一定比圆锥体的体积大。 ( )
(6)圆锥的体积等于和它等底等高圆柱体积的三分之一。 ( )
(7)正方体、长方体、圆柱体、圆锥体的体积都等于底面积×高。
( )
(8)一个圆柱的体积是27立方米,和它等底等高的圆锥的体积是9立
方米。 ( )
√
×
√
×
课堂练习
2.求下面圆锥的体积。(单位:dm)
V圆锥== sh= πr h= π×6 ×20=753.6(立方厘米)
课堂练习
3.一个圆锥的体积是32立方米,它的底面积为16平方米,那么这个圆
锥的高为多少米?
4.—个圆锥体和—个圆柱体的底面积和高都相等,它们的体积之和是
72立方厘米,这个圆锥体的体积是多少立方厘米?
3×32÷16=6(米)
答:这个圆锥的高为6米。
72÷(1+3)=18(立方厘米)
答:这个圆锥的体积为18立方厘米。
课堂练习
5.我班数学小组的同学利用课余时间测量了一堆沙子,得到了以下信
息:底面半径2米,底面直径4米,底面周长12.56米,底面积12.56平
方米,高1.2米,
(1)你能根据这些信息,用不同的方法计算出这堆沙子的体积吗?
(2)比较这些计算方法你发现了什么?
(3)准备把这堆沙填在一个长3.14米,宽2米的沙坑里,请同学们算
一算能填多深?
(1)略;(2)直接应用底面积乘高的方法最简便;
(3)12.56×1.2×÷(3.14×2)=0.8(米)
课后习题
1.填空题。
(1)圆锥的底面是个( );圆锥的侧面是一个( ),展开后
是一个( )。
(2)从圆锥的( )到( )的距离是圆锥的高。
(3)一个圆柱和一个圆锥等底等高时,圆锥的体积是圆柱的体积的
( );圆柱的体积是圆锥的体积的( ) 。
(4)圆柱的体积是18立方厘米,与它等底等高的圆锥的体积是
( )。
圆形
曲面
扇形
顶点
圆心
三倍
6立方厘米
课后习题
1.填空题。
(5)圆锥的体积是18立方厘米,与它等底等高的圆柱的体积是
( )。
(6)一个圆柱和一个圆锥等底等高,他们体积的和是48立方分米,
圆锥的体积是( )。
(7)一个圆柱和一个圆锥等底等高,圆柱的体积比圆锥的体积多7.8
立方米,圆柱的体积是( ),圆锥的体积是( )。
3.9立方米
11.7立方米
54立方厘米
12立方分米
2.求下面圆锥体的体积。
(1)底面积14.7平方厘米,高1分米。
(2)底面周长31.4米,高是3.9米。
(3)底面直径是4厘米,高是15厘米
课后习题
1分米=10厘米 ×14.7×10=49(立方厘米)
31.4÷3.14÷2=5(米) ×3.14×5 ×3.9=102.05(立方米)
×3.14×2 ×15=62.8(立方厘米)
课后习题
3.一个圆锥形沙堆,底面周长50.24米,高6米。这堆沙的体积是多少
立方米?
4.一个圆柱体,底面直径是8米,高是3米,求与它等底等高的圆锥体
的体积。
50.24÷3.14÷2=8(米) ×3.14×8 ×3=200.96(立方米)
答:这堆沙的体积是200.96立方米。
×3.14×4 ×3=50.24(立方米))
答:圆锥的体积是50.24立方米。
课后习题
5.将直角三角形ABC(如图),以AB为边为轴旋转一周,得到的圆锥体积
是V,那么V= 。
6.蒙古包也称“毡包”,是蒙古族传统民居,下图中的蒙古包是由一个
圆柱体和一个圆锥体组成的(单位:米)。这个蒙古包占地多少?内
部的空间约是多少?(得数保留整数。)
×3.14×4 ×3=50.24
50.24
3.14×4 =50.24(平方米)
×50.24×1.2+50.24×2=120.576
≈121(立方米)
