物理:1.4《怎样描述速度变化的快慢》教案(沪科版必修1)
文档属性
| 名称 | 物理:1.4《怎样描述速度变化的快慢》教案(沪科版必修1) |

|
|
| 格式 | rar | ||
| 文件大小 | 161.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2009-07-21 21:26:00 | ||
图片预览



文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第一章 怎样描述物体的运动
4、怎样描述速度变化的快慢
张成进 江苏徐州睢宁魏集中学
★教学目标
(1) 知识与技能
1. 知道物体的速度变化是有快慢之分的,理解加速度的含义及物理意义,知道加速度的定义符号、公式和单位。
1. 知道加速度是矢量,了解加速度的方向。会区分加速度与速度、速度的变化、速度的变化率之间的关系
1. 会用匀变速直线运动的图像求加速度
(1) 过程与方法
1. 通过多媒体课件对生活实例中运动物体速度变化快慢的感受,以及类比法的探究推理,培养学生抽象逻辑思维能力。
1. 培养学生主动、积极的科学探究能力和创新精神。
1. 强化用比值定义的物理思想方法。
(1) 情感态度与价值观
1. 培养学生学习物理的兴趣和积极性及善于区分事物的能力。
★教学重点
1. 加速度的概念及理解。
★教学难点
1. 加速度方向的理解。
1. 加速度与速度之间有关系吗?
★教学过程
引入:
一、加速度
师:同学们,上节课的学习中我们知道用速度—时间图象可以非常直观反映物体速度随时间的变化规律。那请同学们仔细观察下面几个图象,告诉我它们分别反映了怎么的运动规律。
生:甲:A以与正方向同向的速度匀速,B初速度与正方向相反,然后开始减速至零后调头朝着正方向加速度。
乙:AB均是先加速后匀速;
丙:AB均是先加速后匀速。
师:引入提问:乙丙中AB均是先加速度后匀速,那它们是完全一样的运动吗?如果不一样,说出它们的区别。
生:乙中:虽然AB均是先加速后匀速,但它们从零增加到相同的速度所用的时间不同,A的时间小于B的时间,也就是说A的速度增加得比B的速度增加得快。丙中:AB在相同的时间内,速度增加得不一样多,还是A的速度增加得快。
师:好,总的来说就是AB加速过程中速度增加的快慢不同。那我们应该用哪个物理量来描述它们之间的不同呢?是A的速度比B的速度大?还是A的速度增加量比B的速度增加量多?
生:好像可以讲每个时刻A的速度比B的速度大。乙中速度变化量一样,丙中A的速度变化量比B的速度变化量大。
师:若两图中均把A图象往右平移一格呢?
生:说A每个时刻的速度比B的速度大的说法好像不正确了。
师:说得很好。AB之间的不同不在于速度的大小不同,也不是速度变化量的不同,而是速度变化快慢的不同。为了描述物体运动过程中速度变化快慢的不同,现有的物理量无法描述,我们有必要引入一个新的物理量:加速度。
加速度的物理意义:表示物体速度变化的快慢。
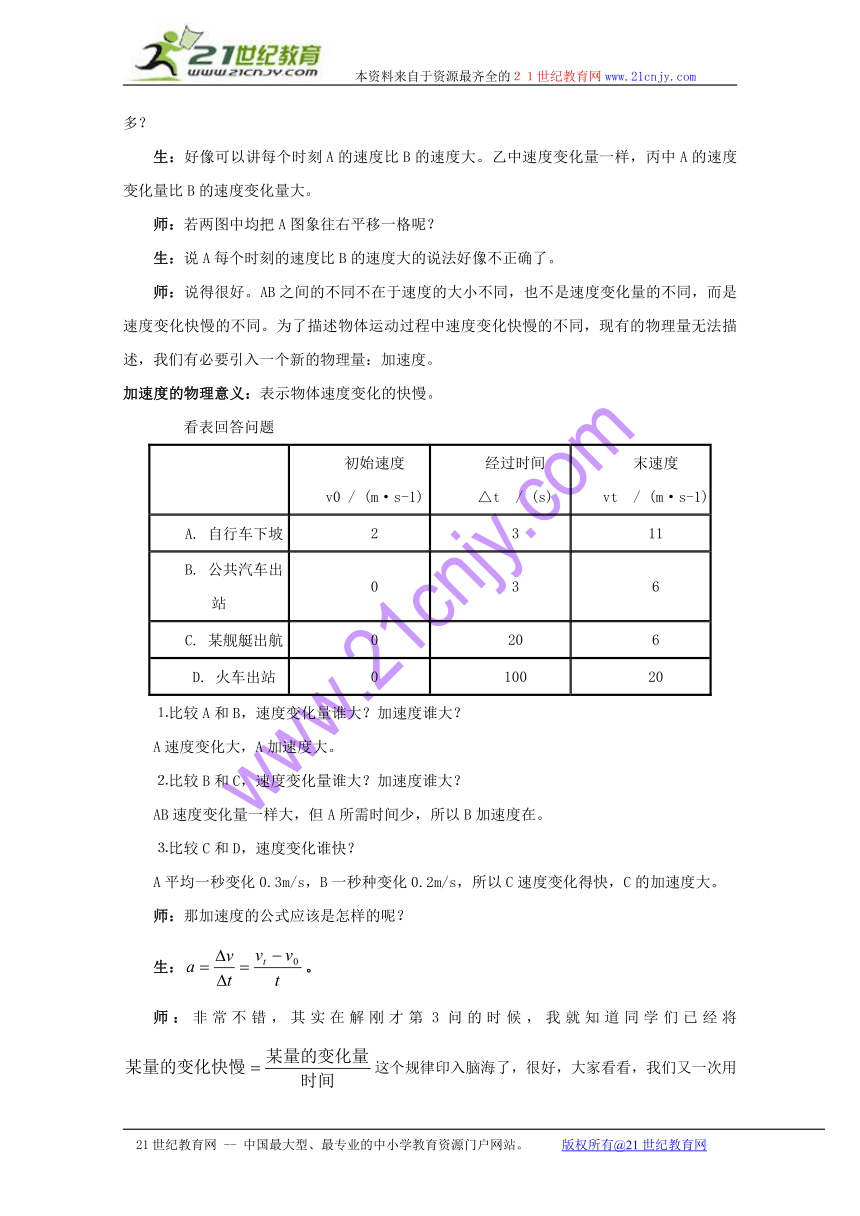
看表回答问题
初始速度v0 / (m·s-1) 经过时间△t / (s) 末速度vt / (m·s-1)
A. 自行车下坡 2 3 11
B. 公共汽车出站 0 3 6
C. 某舰艇出航 0 20 6
D. 火车出站 0 100 20
⒈比较A和B,速度变化量谁大?加速度谁大?
A速度变化大,A加速度大。
⒉比较B和C,速度变化量谁大?加速度谁大?
AB速度变化量一样大,但A所需时间少,所以B加速度在。
⒊比较C和D,速度变化谁快?
A平均一秒变化0.3m/s,B一秒种变化0.2m/s,所以C速度变化得快,C的加速度大。
师:那加速度的公式应该是怎样的呢?
生:。
师:非常不错,其实在解刚才第3问的时候,我就知道同学们已经将这个规律印入脑海了,很好,大家看看,我们又一次用到了比值法来定义物理量。
加速度:速度的变化量与发生这一变化所用时间的比值。通常用a表示。
公式:。
标矢性:矢量
方向:与△V方向相同。
物理意义:表示物体速度变化的快慢和方向的物理量。
单位: m/s2。
三幅图中的小车运动时有加速度吗?请说明理由。
牢记:加速度是速度变化量与时间的比值,速度是矢量,有大小方向,只要大小和方向任一变了,则速度变了,则必有加速度。
二、日常生活中的加速度
师:学到这儿,很多人肯定会想,怎么我在日常生活中没有听说过加速度这个词,是不是日常生活中用不到呢?还是在日常生活中它有另一种说法?比如:我们常说物体走了多远,是指路或位移。说它跑得快是指速度大。加速度在日常生活中的另一种说法是什么呢?
师:其实在日常生活中,加速度并没有相对应的典型词语。一般只能笼统的快和慢。我们常说的快和慢有时指速度,有时指加速度。如下
1、火车经过大提速后,真快。 速度快
2、我这车好,启动快。(就是加速快) 加速度大
3、这个同学素质好,有很好的爆发力,起跑快。 加速度大
三、一维坐标中加速度表示方法
知道了一维坐标中位置、位移、速度的表示方法,同样用公式求加速度时,只需根据“同向为正、反向为负“标出各物理量的正负以后代入公式计算即可,所得结果,同向为正反向为负。
比较大小:-3m/s2与2m/s2
四、经典例题
例1、求下列各种情况下物体的加速度。
一、汽车以20m/s的速度沿正东方向做匀速直线运动。
二、汽车现在速度是5m/s,正东方向,10S后,速度变为15m/s,方向仍为正东方向。
三、汽车现在速度是15m/s,正东方向,10S后,速度变为5m/s,方向仍为正东方向。
四、汽车现在速度是15m/s,正东方向,10S后,速度变为5m/s,方向为正西方向。
解:设正方向:以正东为正方向。
一、初末速度相同=0,=0,所以a=0。
二、,正东方向。
三、,正西方向。
五、,正西方向。
扩展:若以正西方向为正方向呢?
例2、自然界中隼(sǔn)的速度是比较快的,它是田鼠等啮齿类动物的天敌。
假如隼在300m处发现一只田鼠并立即开始直线加速,设隼在2s的时间内,速度从10m/s增大到130m/s,求这只隼的加速度为多大?
解:设初速度方向为正方向,有
五、加速度与速度的关系
师:若已知物体的加速度你能从这个已知量知道哪些信息?
生:我可以知道速度每秒变化2m/s。
师:不错!那是变大还是变小呢?
生:应该是变小吧?
师:为什么呢?
生:因为加速度是负的嘛!
师:是吗?大家仔细看看上面“例1“再回答我这个问题。
生:不是的!好像是a与v同号时,加速;a与v异号时,减速。
师:很好!计算中同号即同向,异号即反向。所以我们要牢记:初速度与加速度方向相同,物体加速;初速度与加速度方向相反,物体减速。物体是加速还是减速由初速度与加速度的方向决定,加速度的大小只能决定速度变化的快慢。
六、速度—时间图象看加速度
师:看引入时的乙、丙两图,思考。
结论:从函数图象的倾斜程度可以看出加速度的大小。
七、加速度与速度的关系
例2、判断下列说法是否正确
A. 从加速度公式可知:加速度a与速度变化量成正比,与时间成反比。
A. 速度很大,加速度肯定很大。
A. 速度很大,加速度可能为0。
A. 速度为0,加速度一定为0。
A. 速度增大,加速度一定增大。
A. 速度减小,加速度一定减小。
A. 速度变化量越大,加速度就越大。
A. 加速度为0,速度一定为0。
A. 加速度很小,速度一定很小。
A. 加速度很大,速度一定很大。
A. 加速度增大,速度一定增大。
A. 加速度减小,速度一定减小。
A. 速度改变越快,加速度就越大。
A. 速度变化率越大,加速度就越大。
解:逐条分析,D项可以这样说明,上抛物体到最高点时,速度为0 ,此时加速度不为0,因为若加速度为0,那物体就应该不再变速,下一时刻速度还应该是0,但事实是物体不会停在空中,会下落,所以加速度不是0.(生动说明物体某一时刻的速度是由上一时刻的速度及加速度共同决定;如我此刻取得的成绩是由今天之前我努力得到的,至于今后会怎样,要看我今天的表现。)
牢记:加速度与速度间无必然联系,若讲速度怎样,加速度就怎样或加速度怎样,速度就怎样,肯定是错的。
例3、物体做匀加速直线运动,加速度为2m/s2,那么任意一秒内(B)
A. 物体的末速度一定等于初速度的2倍
A. 物体的末速度一定比初速度大2m/s
A. 物体在这一秒的初速度比前一秒的末速度大2m/s
A. 物体在这一秒的末速度比前一秒的初速度大2m/s
例4、小木块以5m/s的初速度自由冲上光滑斜面,2S内速度大小变为1m/s,求这段时间内速度变化量。(注意的是题目只告诉了你末速度的大小,并没有讲方向,所以有两个解)
八、科学漫步
了解:某量随时间的变化快慢又可以叫做某量的变化率。
了解:加速度=速度变化快慢=速度变化率=单位时间内速度变化量。
九、平均加速度和瞬时加速度
看图作答:
师:t0时间内,AB的加速度一样吗?
生:一样的。
师:那这段时间内AB的速度变化情况一样吗?
生:不一样,A的图象是一条直线,根据数学知道,我们知道是速度随时间均匀增大,而B是先增加得慢,后增加得快。
师:如同平均速度和瞬时速度一样,加速度同样也有平均加速度与瞬时加速度。用公式求出来的只能是平均加速度,因为它对应的是一段时间,只能求出这段时间内速度的平均变化快慢,要更精确地研究运动,还必须引入瞬时加速度这个物理量。比如:10S内速度从0变到20,用公式求得加速度为2m/s2,只能说明这个过程平均下来每秒速度增加2m/s,并不能说明这个过程中每个一秒内速度都是变化2m/s,有可能在前8秒内从0变到14,在后2秒内从14谈到 20。
系统结构图:
章内概念关系总结:
w.w.w.k.s.5.u.c.o.m
www.
t
v
0
t
v
0
A
A
B
A
乙
甲
C
B
t
v
0
丙
B
12m/s
20m/s
0m/s
v
t
A
t0
V0
B
知道了平均速度就能知道该过程中每个时刻的瞬时速度
整个运动过程中,
瞬时速度始终保持不变。该运动叫做匀速直线运动(理想化)。
整个过程不能保持瞬时速度始终不变。叫做变速运动
但当时间间隔足够
小时,可以把该过程的平
均速度看成该过程内任
一时刻的瞬时速度
因为每个时刻
的速度均不变,所以加速度a=0
速度不断变化,所以加速
度a≠0
速度变化均匀,任何相等时间间隔内速度变化量均一样,即瞬时加速度保持不变,叫做匀变速运动(理想化)。且有
速度变化不均匀,不能保证相等的时间间隔内速度变化量一样,即瞬时加速度一直在变。叫做变加速(度)运动。 ,同样可以当时间间隔足够小时,可以用整个过程的平均加速度近似代表该过程内任一时刻的瞬时加速度。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第一章 怎样描述物体的运动
4、怎样描述速度变化的快慢
张成进 江苏徐州睢宁魏集中学
★教学目标
(1) 知识与技能
1. 知道物体的速度变化是有快慢之分的,理解加速度的含义及物理意义,知道加速度的定义符号、公式和单位。
1. 知道加速度是矢量,了解加速度的方向。会区分加速度与速度、速度的变化、速度的变化率之间的关系
1. 会用匀变速直线运动的图像求加速度
(1) 过程与方法
1. 通过多媒体课件对生活实例中运动物体速度变化快慢的感受,以及类比法的探究推理,培养学生抽象逻辑思维能力。
1. 培养学生主动、积极的科学探究能力和创新精神。
1. 强化用比值定义的物理思想方法。
(1) 情感态度与价值观
1. 培养学生学习物理的兴趣和积极性及善于区分事物的能力。
★教学重点
1. 加速度的概念及理解。
★教学难点
1. 加速度方向的理解。
1. 加速度与速度之间有关系吗?
★教学过程
引入:
一、加速度
师:同学们,上节课的学习中我们知道用速度—时间图象可以非常直观反映物体速度随时间的变化规律。那请同学们仔细观察下面几个图象,告诉我它们分别反映了怎么的运动规律。
生:甲:A以与正方向同向的速度匀速,B初速度与正方向相反,然后开始减速至零后调头朝着正方向加速度。
乙:AB均是先加速后匀速;
丙:AB均是先加速后匀速。
师:引入提问:乙丙中AB均是先加速度后匀速,那它们是完全一样的运动吗?如果不一样,说出它们的区别。
生:乙中:虽然AB均是先加速后匀速,但它们从零增加到相同的速度所用的时间不同,A的时间小于B的时间,也就是说A的速度增加得比B的速度增加得快。丙中:AB在相同的时间内,速度增加得不一样多,还是A的速度增加得快。
师:好,总的来说就是AB加速过程中速度增加的快慢不同。那我们应该用哪个物理量来描述它们之间的不同呢?是A的速度比B的速度大?还是A的速度增加量比B的速度增加量多?
生:好像可以讲每个时刻A的速度比B的速度大。乙中速度变化量一样,丙中A的速度变化量比B的速度变化量大。
师:若两图中均把A图象往右平移一格呢?
生:说A每个时刻的速度比B的速度大的说法好像不正确了。
师:说得很好。AB之间的不同不在于速度的大小不同,也不是速度变化量的不同,而是速度变化快慢的不同。为了描述物体运动过程中速度变化快慢的不同,现有的物理量无法描述,我们有必要引入一个新的物理量:加速度。
加速度的物理意义:表示物体速度变化的快慢。
看表回答问题
初始速度v0 / (m·s-1) 经过时间△t / (s) 末速度vt / (m·s-1)
A. 自行车下坡 2 3 11
B. 公共汽车出站 0 3 6
C. 某舰艇出航 0 20 6
D. 火车出站 0 100 20
⒈比较A和B,速度变化量谁大?加速度谁大?
A速度变化大,A加速度大。
⒉比较B和C,速度变化量谁大?加速度谁大?
AB速度变化量一样大,但A所需时间少,所以B加速度在。
⒊比较C和D,速度变化谁快?
A平均一秒变化0.3m/s,B一秒种变化0.2m/s,所以C速度变化得快,C的加速度大。
师:那加速度的公式应该是怎样的呢?
生:。
师:非常不错,其实在解刚才第3问的时候,我就知道同学们已经将这个规律印入脑海了,很好,大家看看,我们又一次用到了比值法来定义物理量。
加速度:速度的变化量与发生这一变化所用时间的比值。通常用a表示。
公式:。
标矢性:矢量
方向:与△V方向相同。
物理意义:表示物体速度变化的快慢和方向的物理量。
单位: m/s2。
三幅图中的小车运动时有加速度吗?请说明理由。
牢记:加速度是速度变化量与时间的比值,速度是矢量,有大小方向,只要大小和方向任一变了,则速度变了,则必有加速度。
二、日常生活中的加速度
师:学到这儿,很多人肯定会想,怎么我在日常生活中没有听说过加速度这个词,是不是日常生活中用不到呢?还是在日常生活中它有另一种说法?比如:我们常说物体走了多远,是指路或位移。说它跑得快是指速度大。加速度在日常生活中的另一种说法是什么呢?
师:其实在日常生活中,加速度并没有相对应的典型词语。一般只能笼统的快和慢。我们常说的快和慢有时指速度,有时指加速度。如下
1、火车经过大提速后,真快。 速度快
2、我这车好,启动快。(就是加速快) 加速度大
3、这个同学素质好,有很好的爆发力,起跑快。 加速度大
三、一维坐标中加速度表示方法
知道了一维坐标中位置、位移、速度的表示方法,同样用公式求加速度时,只需根据“同向为正、反向为负“标出各物理量的正负以后代入公式计算即可,所得结果,同向为正反向为负。
比较大小:-3m/s2与2m/s2
四、经典例题
例1、求下列各种情况下物体的加速度。
一、汽车以20m/s的速度沿正东方向做匀速直线运动。
二、汽车现在速度是5m/s,正东方向,10S后,速度变为15m/s,方向仍为正东方向。
三、汽车现在速度是15m/s,正东方向,10S后,速度变为5m/s,方向仍为正东方向。
四、汽车现在速度是15m/s,正东方向,10S后,速度变为5m/s,方向为正西方向。
解:设正方向:以正东为正方向。
一、初末速度相同=0,=0,所以a=0。
二、,正东方向。
三、,正西方向。
五、,正西方向。
扩展:若以正西方向为正方向呢?
例2、自然界中隼(sǔn)的速度是比较快的,它是田鼠等啮齿类动物的天敌。
假如隼在300m处发现一只田鼠并立即开始直线加速,设隼在2s的时间内,速度从10m/s增大到130m/s,求这只隼的加速度为多大?
解:设初速度方向为正方向,有
五、加速度与速度的关系
师:若已知物体的加速度你能从这个已知量知道哪些信息?
生:我可以知道速度每秒变化2m/s。
师:不错!那是变大还是变小呢?
生:应该是变小吧?
师:为什么呢?
生:因为加速度是负的嘛!
师:是吗?大家仔细看看上面“例1“再回答我这个问题。
生:不是的!好像是a与v同号时,加速;a与v异号时,减速。
师:很好!计算中同号即同向,异号即反向。所以我们要牢记:初速度与加速度方向相同,物体加速;初速度与加速度方向相反,物体减速。物体是加速还是减速由初速度与加速度的方向决定,加速度的大小只能决定速度变化的快慢。
六、速度—时间图象看加速度
师:看引入时的乙、丙两图,思考。
结论:从函数图象的倾斜程度可以看出加速度的大小。
七、加速度与速度的关系
例2、判断下列说法是否正确
A. 从加速度公式可知:加速度a与速度变化量成正比,与时间成反比。
A. 速度很大,加速度肯定很大。
A. 速度很大,加速度可能为0。
A. 速度为0,加速度一定为0。
A. 速度增大,加速度一定增大。
A. 速度减小,加速度一定减小。
A. 速度变化量越大,加速度就越大。
A. 加速度为0,速度一定为0。
A. 加速度很小,速度一定很小。
A. 加速度很大,速度一定很大。
A. 加速度增大,速度一定增大。
A. 加速度减小,速度一定减小。
A. 速度改变越快,加速度就越大。
A. 速度变化率越大,加速度就越大。
解:逐条分析,D项可以这样说明,上抛物体到最高点时,速度为0 ,此时加速度不为0,因为若加速度为0,那物体就应该不再变速,下一时刻速度还应该是0,但事实是物体不会停在空中,会下落,所以加速度不是0.(生动说明物体某一时刻的速度是由上一时刻的速度及加速度共同决定;如我此刻取得的成绩是由今天之前我努力得到的,至于今后会怎样,要看我今天的表现。)
牢记:加速度与速度间无必然联系,若讲速度怎样,加速度就怎样或加速度怎样,速度就怎样,肯定是错的。
例3、物体做匀加速直线运动,加速度为2m/s2,那么任意一秒内(B)
A. 物体的末速度一定等于初速度的2倍
A. 物体的末速度一定比初速度大2m/s
A. 物体在这一秒的初速度比前一秒的末速度大2m/s
A. 物体在这一秒的末速度比前一秒的初速度大2m/s
例4、小木块以5m/s的初速度自由冲上光滑斜面,2S内速度大小变为1m/s,求这段时间内速度变化量。(注意的是题目只告诉了你末速度的大小,并没有讲方向,所以有两个解)
八、科学漫步
了解:某量随时间的变化快慢又可以叫做某量的变化率。
了解:加速度=速度变化快慢=速度变化率=单位时间内速度变化量。
九、平均加速度和瞬时加速度
看图作答:
师:t0时间内,AB的加速度一样吗?
生:一样的。
师:那这段时间内AB的速度变化情况一样吗?
生:不一样,A的图象是一条直线,根据数学知道,我们知道是速度随时间均匀增大,而B是先增加得慢,后增加得快。
师:如同平均速度和瞬时速度一样,加速度同样也有平均加速度与瞬时加速度。用公式求出来的只能是平均加速度,因为它对应的是一段时间,只能求出这段时间内速度的平均变化快慢,要更精确地研究运动,还必须引入瞬时加速度这个物理量。比如:10S内速度从0变到20,用公式求得加速度为2m/s2,只能说明这个过程平均下来每秒速度增加2m/s,并不能说明这个过程中每个一秒内速度都是变化2m/s,有可能在前8秒内从0变到14,在后2秒内从14谈到 20。
系统结构图:
章内概念关系总结:
w.w.w.k.s.5.u.c.o.m
www.
t
v
0
t
v
0
A
A
B
A
乙
甲
C
B
t
v
0
丙
B
12m/s
20m/s
0m/s
v
t
A
t0
V0
B
知道了平均速度就能知道该过程中每个时刻的瞬时速度
整个运动过程中,
瞬时速度始终保持不变。该运动叫做匀速直线运动(理想化)。
整个过程不能保持瞬时速度始终不变。叫做变速运动
但当时间间隔足够
小时,可以把该过程的平
均速度看成该过程内任
一时刻的瞬时速度
因为每个时刻
的速度均不变,所以加速度a=0
速度不断变化,所以加速
度a≠0
速度变化均匀,任何相等时间间隔内速度变化量均一样,即瞬时加速度保持不变,叫做匀变速运动(理想化)。且有
速度变化不均匀,不能保证相等的时间间隔内速度变化量一样,即瞬时加速度一直在变。叫做变加速(度)运动。 ,同样可以当时间间隔足够小时,可以用整个过程的平均加速度近似代表该过程内任一时刻的瞬时加速度。
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 开篇 激动人心的万千体验
- 01物理学——理性的追求
- 02物理学——人类文明的奇葩
- 03学物理——探究求真
- 第一章 怎样描述物体的运动
- 1 走近运动
- 2 怎样描述运动的快慢
- 3 怎样描述运动的快慢(续)
- 4 怎样描述速度变化的快慢
- 第二章 研究匀变速直线运动的规律
- 1 伽利略对落体运动的研究
- 2 自由落体运动的规律
- 3 匀变速直线运动的规律
- 4 匀变速直线运动规律的应用
- 第三章 力与相互作用
- 1 牛顿第三定律
- 2 弹力
- 3 摩擦力
- 4 分析物体的受力
- 第四章 怎样求合力与分力
- 1 怎样求合力
- 2 怎样分解力
- 3 共点力的平衡及其应用
- 第五章 研究力和运动的关系
- 1 牛顿第一定律
- 2 探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 牛顿运动定律的案例分析
- 5 超重与失重
