专题02二次函数、三次函数、指对数函数-2017-2018学年下学期期末复习备考高二数学(文)备考热点难点突破练(江苏版)
文档属性
| 名称 | 专题02二次函数、三次函数、指对数函数-2017-2018学年下学期期末复习备考高二数学(文)备考热点难点突破练(江苏版) |

|
|
| 格式 | zip | ||
| 文件大小 | 169.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-22 00:00:00 | ||
图片预览



文档简介
填空题
1. 若方程a·4x+2x+1+1=0至少有一个正根,则实数a的取值范围是____.
答案: -3
解析:由题意,问题等价于,其表示的区域如图所示,
可看作是可行域内的点到点(1,2)连线的斜率,点(1,2)与点(-1,0)连线的斜率取得最大值1,然后绕点(1,2)顺时针旋转至(-3,1)时,取得斜率的最小值,所以∈.
答案: ∈
3. 已知函数f(x)=x2+|x-a|-1有大于0的零点,则实数a的取值范围是________.
解析1:记f(x)=x2+|x-a|-1=,
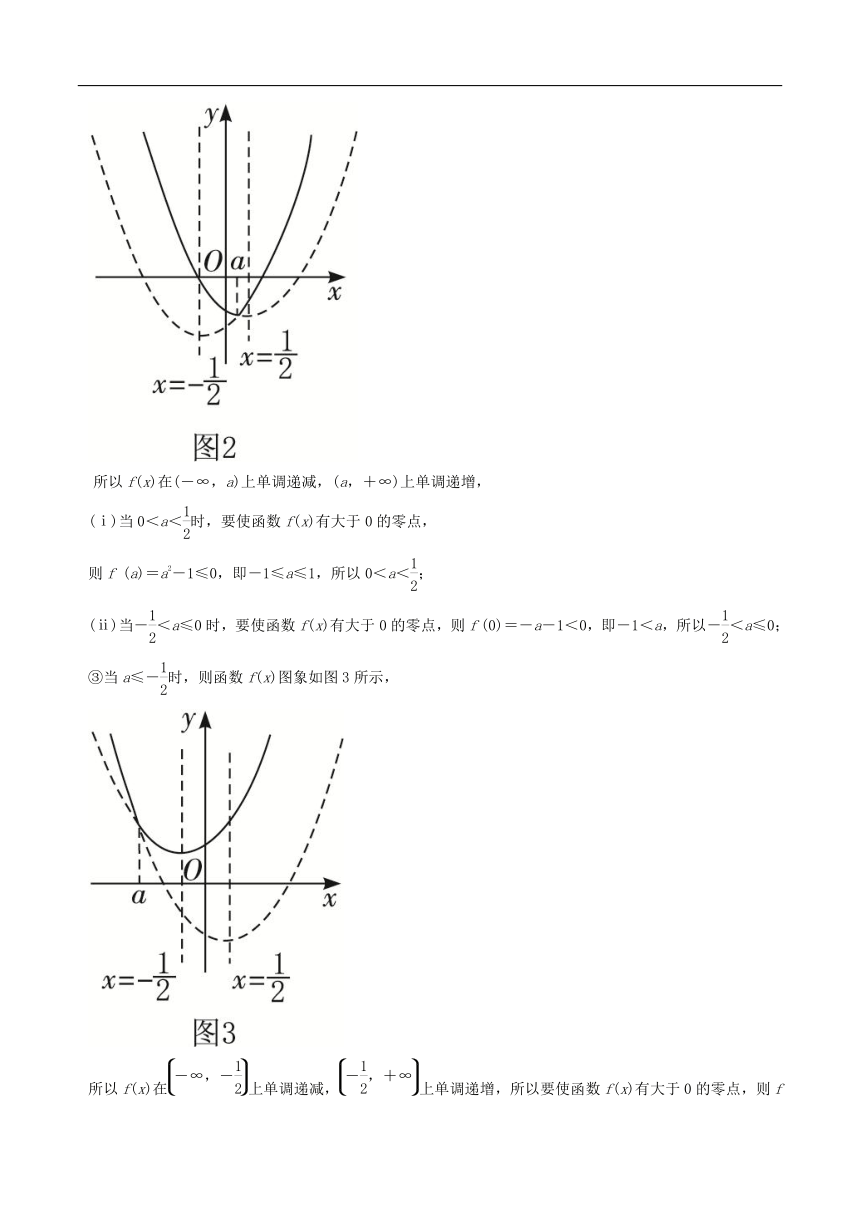
②当-<a<时,则函数f(x)图象如图2所示,
所以f(x)在(-∞,a)上单调递减,(a,+∞)上单调递增,
(ⅰ)当0<a<时,要使函数f(x)有大于0的零点,
则f (a)=a2-1≤0,即-1≤a≤1,所以0<a<;
(ⅱ)当-<a≤0时,要使函数f(x)有大于0的零点,则f (0)=-a-1<0,即-1<a,所以-<a≤0;
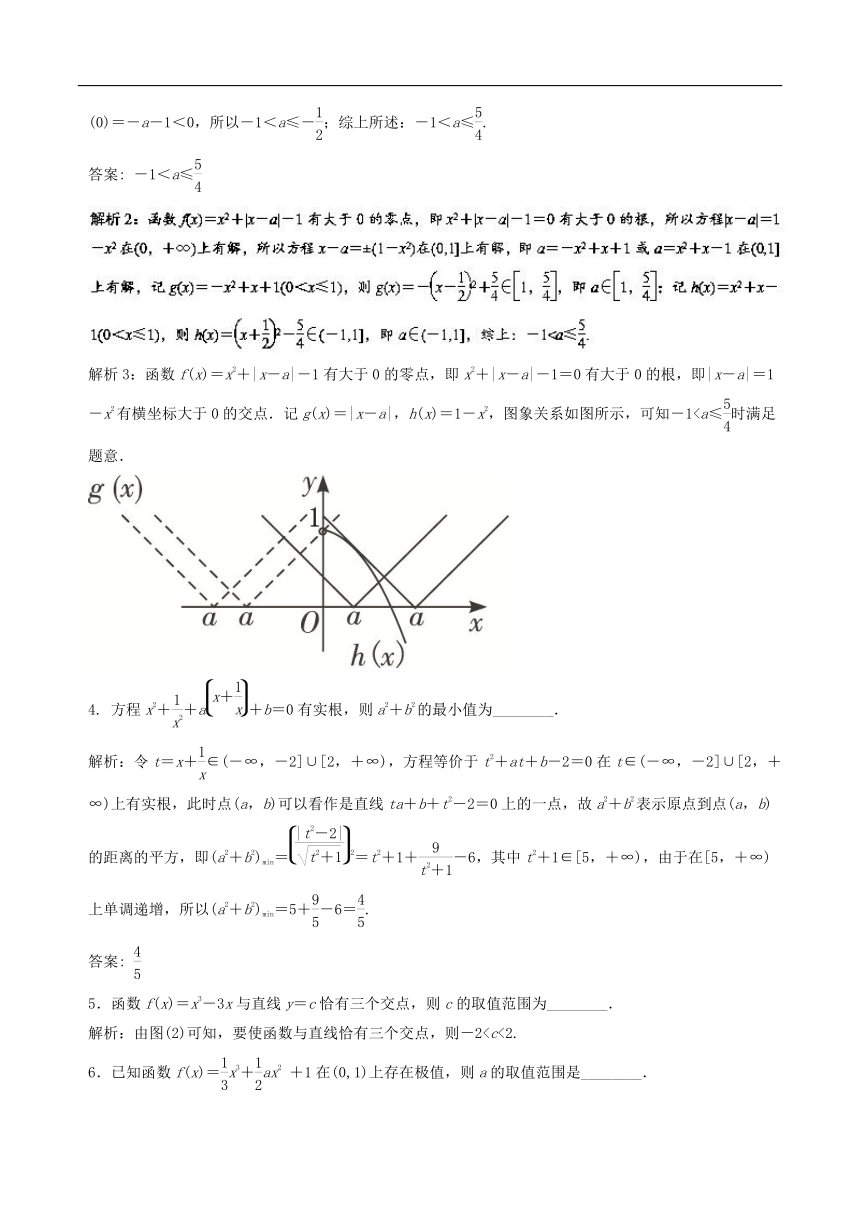
③当a≤-时,则函数f(x)图象如图3所示,
所以f(x)在上单调递减,上单调递增,所以要使函数f(x)有大于0的零点,则f (0)=-a-1<0,所以-1<a≤-;综上所述:-1<a≤.
答案: -1<a≤
解析3:函数f(x)=x2+|x-a|-1有大于0的零点,即x2+|x-a|-1=0有大于0的根,即|x-a|=1-x2有横坐标大于0的交点.记g(x)=|x-a|,h(x)=1-x2,图象关系如图所示,可知-1
解析:令t=x+∈(-∞,-2]∪[2,+∞),方程等价于t2+at+b-2=0在t∈(-∞,-2]∪[2,+∞)上有实根,此时点(a,b)可以看作是直线ta+b+t2-2=0上的一点,故a2+b2表示原点到点(a,b)的距离的平方,即(a2+b2)min=2=t2+1+-6,其中t2+1∈[5,+∞),由于在[5,+∞)上单调递增,所以(a2+b2)min=5+-6=.
答案:
5.函数f(x)=x3-3x与直线y=c恰有三个交点,则c的取值范围为________.
解析:由图(2)可知,要使函数与直线恰有三个交点,则-2
解析:f′(x) =x2+ax在(0,1)上存在非重根,所以0<-a<1,即a的取值范围是(-1,0).
7.已知函数f(x)=x3+ax2+1在(0,1)上存在单调递减区间,则实数a的取值范围是________.
解析:f′(x)=x2+ax<0在(0,1)上有解,化为a<-x在(0,1)上有解,即a<0.
8.已知函数f(x)=ax3-3x2 +1,若f(x)存在唯一的零点x0,且x0>0,则a的取值范围是________.
9. 已知函数f(x)=(x2-1)(x2+ax+b)的图象关于直线x=3对称,则函数f(x)的值域为________.
解析:由题知f (-1)=0,f (1)=0,因为函数f(x)的图象关于直线x=3对称,所以 f (7)=f (-1)=0且f (5)=f (1)=0,即,解得a=-12,b=35,
所以f(x)=(x2-1)( x2-12x+35)= (x+1)(x-1)(x-5)(x-7)=(x2-6x+5)(x2-6x-7),
设t=x2-6x-1(t≥-10),则f (t)=(t+6)(t-6)=t2-36≥-36,故函数f(x)的值域为[-36,+∞).
10. 若函数f(x)=(x-a)2|x-a|-x2|x|+a在(0,1)存在零点,则实数a的取值范围是________.
解析:注意到f (a-x)=(-x)2|-x|-(a-x)2|a-x|+a=-(x-a)2|x-a|+x2|x|+a,所以f(x)+f (a-x)=2a,从而y=f(x)的图象关于点对称,下面考虑y=f(x)在的图象.
当a>0时,f(x)=(x-a)2|x-a|-x2|x|+a=,易得f(x)在上单调递减,因为y=f(x)的图象关于点对称,所以f(x)在R上单调递减;
因为f(x)在(0,1)上有零点,所以[a2 |a|+a] ·[(a-1)2 |a-1|+(a -1)]<0,即或解得0
当a<0时,同理可得f(x)在R上单调递增,同样有f (0)·f (1)<0,即
即解得-1
12.方程|ex-1|+ax+1=0有两个不同的解,则实数a的取值范围是________.
解析:化为|ex-1|+1=-ax,令f(x)=|ex-1|+1=,作出图象可知,y=-ax与f(x)应在x≥0上有两个不同的交点,考虑相切时,设切点P(x0,y0),则?x0=1,此时P(1,e),所以-a>e,得a<-e.
13.定义在R上的函数f(x)满足:f′(x)>f(x)恒成立,若x1
14.已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=________.
解析:函数的零点满足x2-2x=-a(ex-1+e-x+1),设g(x)=ex-1+e-x+1,则g′(x)=ex-1-e-x+1=ex-1-=,当g′(x)=0时,x=1,当x<1时,g′(x)<0,函数g(x)单调递减,当x>1时,g′(x)>0,函数g(x)单调递增,当x=1时,函数取得最小值g(1)=2,设h(x)=x2-2x,当x=1时,函数取得最小值-1,若-a>0,函数h(x)与函数ag(x)没有交点,若-a<0,-ag(1)=h(1)时,函数h(x)与函数ag(x)有一个交点,即-a×2=-1,解得a=.
解答题
15. 已知函数f(x)=x2-2x+a(a∈R)的最小值为0,记函数g(x)=.
(1)求实数a的值;
(2)若不等式g(2x)-m·2x+1≤0对任意x∈[-1,1]都成立,求实数m的取值范围;
(3)若关于x的方程g(|f(x)-1|)=k-有六个不相等的实数根,求实数k的取值范围.
解析:(1)f(x)=x2-2x+a=(x-1)2+a-1,即有x=1时f(x)取最小值a-1,令a-1=0,解得:a=;
答案: 1
令t=∈,则问题转化为不等式m≥(t-1)2对任意的t∈都成立,记h(t)=(t-1)2,则h(t)max=h=,所以m的取值范围是;
答案:
(3)当x=0,2时,f(x)-1=0,
所以x=0,2不是方程的解;
当x≠0且x≠2时,令t=|f(x)-1|=|x2-2x|,
则当x∈(-∞,0)时,t=x2-2x单调递减,且t∈(0,+∞),
当x∈(0,1]时,t=2x-x2单调递增,且t∈(0,1],
当x∈(1,2)时,t=2x-x2单调递减,且t∈(0,1),
当x∈(2,+∞)时,t=x2-2x单调递增,且t∈(0,+∞);
故原方程有六个不相等的实数根可转化为t2-(k+2)t+(2k+1)=0有两个不相等的实数根t1,t2,其中0
记φ(t)=t2-(k+2)t+(2k+1),则,所以实数k的取值范围是.
答案:
16. 已知函数f(x)=.
(1)当a=b=1时,求满足f(x)=3x的x的取值;
(2)若函数f(x)是定义在R上的奇函数,
①存在t∈R,不等式f(t2-2t)
解析:(1)由题意=3x,得3·(3x)2+2·3x-1=0,解得3x=-1(舍)或3x=,所以x=-1;
答案: -1
①f(x)==,对任意x1,x2∈R,x1<x2有:f(x1)-f(x2)==
因为x1<x2,所以3x2-3x1>0,所以f(x1)>f(x2),f(x)在R上递减.
因为f (t2-2t)<f (2t2-k),所以t2-2t>2t2-k,即t2+2t-k<0在t∈R时有解
所以Δ=4+4k>0,解得:k>-1,所以k的取值范围为(-1,+∞);
②因为f(x)·[g(x)+2]=(3-x-3x),所以g(x)=-2=3x+3-x,所以g(2x)=32x+3-2x=(3x+3-x)2-2,不等式g(2x)≥mg(x)-11恒成立,即(3x+3-x)2-2≥m(3x+3-x)-11恒成立,令t=3x+3-x∈[2,+∞),即t2-mt+9≥0对t∈[2,+∞)恒成立,设h(t)=t2-mt+9,t∈[2,+∞)
①当≤2时,即m≤4时,h(t)min=h(2)=13-2m≥0,解得m≤4;
②当>2时,即m>4时,h(t)min=h=-+9≥0,解得4<m≤6;
综上m≤6,所以m的最大值为6.
答案: 6
17. 已知函数f(x)=x3-x.
(1) 求曲线y=f(x)在点M(t,f(t))处的切线方程;
(2) 设a>0,如果过点(a,b)可作曲线y=f(x)的三条切线,证明:-a
(2) 将(a,b)代入y=(3t2-1)x-2t3,得b=(3t2-1)a-2t3.过点(a,b)可作曲线y=f(x)的三条切线等价于方程2t3-3at2 +a+b=0有三个相异的实数根,记g(t)=2t3-3at2+a+b,则g′(t)=6t2-6at=6t(t-a).
当t变化时,g(t),g′(t)变化情况如表所示:
t
(-∞,0)
0
(0,a)
a
(a,+∞)
g′(t)
+
0
-
0
+
g(t)
↗
极大极
a+b
?
极小值
b-f (a)
↗
由g(t)的单调性,当极大值a+b<0或极小值b-f (a)>0时,方程g(t)=0最多有一个实数根;当a+b=0时,解方程g(t)=0得t=0,t=,即方程g(t)=0只有两个相异的实数根;当b-f (a)=0时,解方程g(t)=0得t=-,t=a,即方程g(t)=0只有两个相异的实数根.
综上,如果过(a,b)可作曲线y=f(x)三条切线,即g(t)=0有三个相异的实数根,则
即-a
(1) 求以P(2,f(2))为切点的切线方程,并证明此切线恒过一个定点;
(2) 若g(x)≤kx对一切x∈[0,2]恒成立,求k的最小值h(a)的表达式;
(3) 设a>0,求y=g(x)的单调增区间.
① 当a≥时,|x2- 3x+a|max在x=0时取得,所以h(a)=a;
② 当a<时,|x2-3x+a|max=max=由①②,得g(a)=
(3) f(x)=x3-3x2+ax,f′(x)=3x2-6x+a=3(x-1)2+a-3,
令f(x)=0,得x=0或x2-3x+a=0,
当a<时,由x2-3x+a=0,解得x1=-,x2=+,令f′(x)=0,得3(x-1)2+a-3=0,当a<3时,由3(x-1)2+a-3=0,解得x3=1-,x4=1+.
1) 当a≥3时,y=g(x)的单调增区间为(0,+∞);
2) 当≤a<3时,y=g(x)的单调增区间为(0,x3)和(x4,+∞);
3) 当0
(1)当a=1时,求函数f(x)的单调区间;
(2)①若存在实数x,满足f(x)<0,求实数a的取值范围;
②若有且只有唯一整数x0,满足f(x0)<0,求实数a的取值范围.
当x>1时,a>;当x<1时,a<.
记g(x)=,g′(x)==,所以g(x)在区间(-∞,0)和(,+∞)上为增函数,在(0,1)和(1,)上为减函数.
所以当x>1时,a>g()=4e,当x<1时,a
②由①知a<1时,x0∈(-∞,1),由f(x0)<0,得g(x0)>a,又g(x)在区间(-∞,0)上单调递增,在(0,1)上单调递减,且g(0)=1>a,所以g(-1)≤a,即a≥,所以≤a<1;
当a>4e时,x0∈(1,+∞),由f(x0)<0,得g(x0)
20. 已知函数f(x)=ex-ax-2,其中a为常数.
(1)求函数f(x)的单调区间;
(2)已知a=1,k为整数,若对任意x∈(0,+∞),都有(x-k)f′(x)+x+1>0都成立,求k的最大值.
解析:(1)函数f(x)的定义域为(-∞,+∞),f′(x)=ex-a.
若a≤0时,则f′(x)>0,所以f(x)在(-∞,+∞)上单调递增;
若a>0时,则当x∈(-∞,ln a)时,f′(x)<0,当x∈(ln a,+∞)时,f′(x)>0,所以f(x)在(-∞,ln a)上递减,在(ln a,+∞)上递增.
因为当x∈(0,x0)时,g′(x)<0,当x∈(x0,+∞)时,g′(x)>0,
所以g(x)在(0,+∞)上的最小值为g(x0)=+x0,所以k<+x0.又因为g′(x0)=e-x0-2=0,所以e=x0+2,所以k
(1)若f(x)≥0,求a的值;
(2)设m为整数,且对于任意正整数n,(1+)(1+)…(1+)
对f(x)求导得f′(x)=1-=(x>0),①若a≤0,则f′(x)>0恒成立,f(x)在(0,+∞)上递增,则x∈(0,1)时,f(x)<0,所以a≤0不合题意;
②若a>0,则x∈(0,a)时f′(x)<0,f(x)递减,x∈(a,+∞)时,f′(x)>0,f(x)递增,f(x)min=f (a)=a-1-a ln a,令g(a)=a-1-a ln a,g′(a)=1-a·-ln a=-ln a,a∈(0,1)时,g(a)递增,a∈(1,+∞)时,g(a)递减,g(a)≤g(a)max=g(1)=0,故当且仅当a=1时,f(x)min=f (1)=0,符合题意.综上,a=1.
(2)由(1)得x-1-ln x≥0在 (0,+∞)上恒成立,所以x-1≥ln x,令x=1+,即有≥ln(1+),因为ln[(1+)(1+)…(1+)]=ln(1+)+ln(1+)+…+ln(1+)≤++…+=<1,所以若对于任意正整数n,(1+)(1+)…(1+)
同课章节目录
