物理:5.4《平衡条件的应用》教案(鲁科版必修1)
文档属性
| 名称 | 物理:5.4《平衡条件的应用》教案(鲁科版必修1) |  | |
| 格式 | rar | ||
| 文件大小 | 112.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2009-07-22 08:53:00 | ||
图片预览

文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
第四节 平衡条件的应用
从容说课
力的平衡要有正确的思路:首先确定研究对象,
其次是正确分析物体的受力,然后根据平衡条件列方程求解.对于比较简单的问题,可以用直角三角形的知识求解,对于不成直角的受力问题可以用正交分解方法求解.
三维目标
知识与技能
1.知道共点力作用下物体的平衡概念.
2.掌握在共点力作用下物体的平衡条件.
3.知道如何用实验验证共点力作用下的物体的平衡条件.
4.应用共点力的平衡条件解决具体问题.
过程与方法
1.正确判断物体的运动状态,培养学生的观察和鉴别能力.
2.进一步培养学生分析物体受力的能力.
3.应用平衡条件解决实际问题的能力.
情感态度与价值观
1.了解运动和静止的相对性,培养学生的辩证唯物主义观点.
2.通过对周围处于静止状态的物体的观察和实验,总结出力的平衡条件,再用这个理论来解决和处理实际问题,使学生树立正确的认识观.
通过对物体受力分析图的绘画,使学生了解到物理学中的对称美.
教学设计
教学重点 1.共点力的平衡条件.
2.熟练运用共点力的平衡条件,解决平衡状态下有关力的计算.
3.进一步熟练受力分析的方法.
教学难点 1.物体的受力分析.
2.物体在什么条件下,可以认为是受到共点力作用?
3.物体受到三个不在一条直线上的力作用而处于平衡状态时,这三个力一定共点.
教具准备 投影仪、投影片.
课时安排 1课时
教学过程
导入新课式
1.用投影片出示复合题:
(1)如果一个物体能够保持_________或_________,我们就说物体处于平衡状态.
(2)当物体处于平衡状态时:
a.物体所受各个力的合力等于_________,这就是物体在共点力作用下的平衡条件.
b.它所受的某一个力与它所受的其余外力的合力关系是_________.
2.学生回答问题后,教师进行评价和纠正.
3.引入:本节课我们来运用共点力的平衡条件求解一些实际问题.
推进新课
1.共点力作用下物体的平衡条件的应用举例:
用投影片出示例题1:
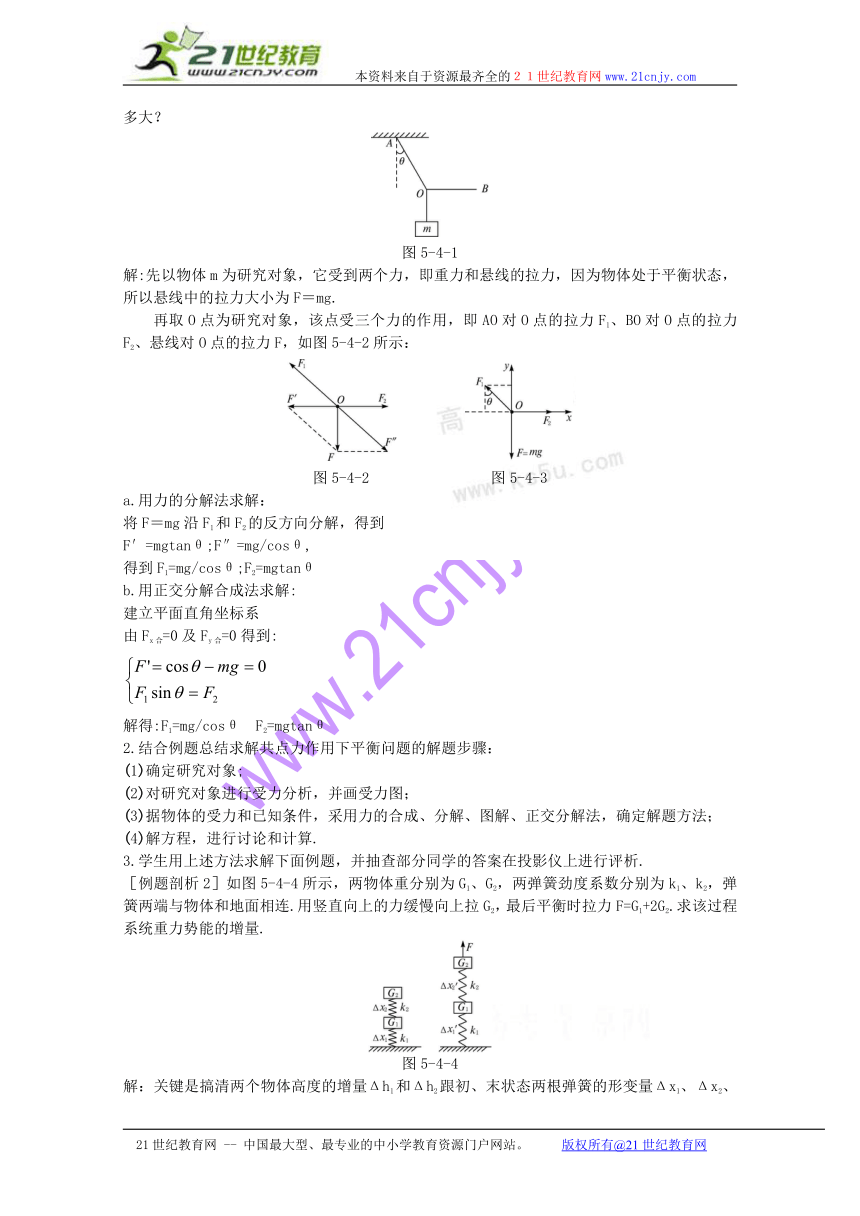
[例题剖析1]如图5-4-1所示.细线的一端固定于A点,线的中点挂一质量为m的物体,另一端B用手拉住,当AO与竖直方向成θ角,OB沿水平方向时,AO及BO对O点的拉力分别是多大?
图5-4-1
解:先以物体m为研究对象,它受到两个力,即重力和悬线的拉力,因为物体处于平衡状态,所以悬线中的拉力大小为F=mg.
再取O点为研究对象,该点受三个力的作用,即AO对O点的拉力F1、BO对O点的拉力F2、悬线对O点的拉力F,如图5-4-2所示:
图5-4-2 图5-4-3
a.用力的分解法求解:
将F=mg沿F1和F2的反方向分解,得到
F′=mgtanθ;F″=mg/cosθ,
得到F1=mg/cosθ;F2=mgtanθ
b.用正交分解合成法求解:
建立平面直角坐标系
由Fx合=0及Fy合=0得到:
解得:F1=mg/cosθ F2=mgtanθ
2.结合例题总结求解共点力作用下平衡问题的解题步骤:
(1)确定研究对象;
(2)对研究对象进行受力分析,并画受力图;
(3)据物体的受力和已知条件,采用力的合成、分解、图解、正交分解法,确定解题方法;
(4)解方程,进行讨论和计算.
3.学生用上述方法求解下面例题,并抽查部分同学的答案在投影仪上进行评析.
[例题剖析2]如图5-4-4所示,两物体重分别为G1、G2,两弹簧劲度系数分别为k1、k2,弹簧两端与物体和地面相连.用竖直向上的力缓慢向上拉G2,最后平衡时拉力F=G1+2G2.求该过程系统重力势能的增量.
图5-4-4
解:关键是搞清两个物体高度的增量Δh1和Δh2跟初、末状态两根弹簧的形变量Δx1、Δx2、Δx1′、Δx2′间的关系.
无拉力F时:Δx1=(G1+G2)/k1,Δx2=G2/k2,(Δx1、Δx2为压缩量)
加拉力F时:Δx1′=G2/k1,Δx2′=(G1+G2)/k2,(Δx1′、Δx2′为伸长量)
而Δh1=Δx1+Δx1′,Δh2=(Δx1′+Δx2′)+(Δx1+Δx2)
系统重力势能的增量ΔEp=G1·Δh1+G2·Δh2
整理后可得:ΔEp=(G1+2G2)()
4.讲解有关斜面问题的处理方法
[例题剖析3]如图5-4-5所示,将重力为G的物体A放在倾角θ的斜面上,物体与斜面间的动摩擦因数为μ,那么对A施加一个多大的水平力F1,可使物体沿斜面匀速上滑?
分析本题:
图5-4-5
a.定物体A为研究对象
b.对物体A进行受力分析:
物体A共受四个力的作用:竖直向下的重力G、水平向右的力F1、垂直于斜面斜向上方的支持力F2、平行于斜面向下的滑动摩擦力F3,其中G和F1是已知的.由滑动摩擦定律F3=μF2可求得F2和F3,就可以求出μ.
c.画出物体的受力图如图5-4-6.
d.本题采用正交分解法:
图5-4-6
对于斜面,常取平行于斜面的方向为x轴,垂直于斜面的方向为y轴,将力沿这两个方向分解,应用平衡条件求解:
e.用投影片展示本题的解题过程:
解:取平行于斜面的方向为x轴,垂直于斜面的方向为y轴,分别在这两个方向上应用平衡条件求解,由平衡条件可知,在这两个方向上的合力Fx合和Fy合应分别等于零,即
Fx合=F3-F1cosθ+Gsinθ=0
Fy合=F2-F1sinθ-Gcosθ=0
并且F3=F2·μ
解得:F1=.
5.巩固训练
如图5-4-7所示,重为G=10 N的小球在竖直挡板作用下静止在倾角为θ=30°的光滑斜面上,已知挡板也是光滑的,求:
图5-4-7
(1)挡板对小球弹力的大小;
(2)斜面对小球弹力的大小.
课堂小结
本节课我们主要学习了以下几点:
1.应用共点力平衡条件解题时常用的方法——力的合成法、力的分解法、正交分解法.
2.解共点力作用下物体平衡问题的一般步骤:
(1)确定研究对象;
(2)对所选研究对象进行受力分析,并画出受力示意图;
(3)分析研究对象是否处于平衡状态;
(4)运用平衡条件,选用适当方法,列出平衡方程求解.
布置作业
练习1.如图5-4-8所示,一个半球形的碗放在桌面上,碗口水平,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°.两小球的质量比为(A)
图5-4-8
A. B. C. D.
练习2.如图5-4-9所示,人重600 N,木板重400 N,人与木板、木板与地面间的动摩擦因数皆为0.2.现在人用水平力拉绳,使他与木块一起向右匀速运动,则(BC)
图5-4-9
A.人拉绳的力是200 N B.人拉绳的力是100 N
C.人的脚给木块摩擦力向右 D.人的脚给木块摩擦力向左
练习3.如图5-4-10所示,两个完全相同的小球,重力大小为G,两物体与地面间的动摩擦因数均为μ,一根轻绳的两端固定在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳的夹角为θ.求当F至少为多大时,两球将会发生相对滑动?(F=)
图5-4-10
练习4.如图5-4-11所示,两个固定的光滑硬杆OA与OB,夹角为θ,各套一轻环C、D,且C、D用细绳相连.现在用一水平恒力F沿OB方向拉环D,当两环平衡时,绳子的拉力是多大 (F/sinθ)
图5-4-11 图5-4-12
练习5.如图5-4-12所示,均匀杆AB重为G,A端用细绳吊在O点,在B端加一水平力F,使AB静止,此时杆与水平方向夹角为α,细绳与竖直方向成θ角.则(B)
A.拉力F一定大于G B.绳子拉力T一定大于G
C.AB杆与水平夹角α必小于θ D.F足够大时细绳可在水平方向上
板书设计
共点力平衡条件的应用
活动与探究
观察高压电线的塔架有何特点.
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
第四节 平衡条件的应用
从容说课
力的平衡要有正确的思路:首先确定研究对象,
其次是正确分析物体的受力,然后根据平衡条件列方程求解.对于比较简单的问题,可以用直角三角形的知识求解,对于不成直角的受力问题可以用正交分解方法求解.
三维目标
知识与技能
1.知道共点力作用下物体的平衡概念.
2.掌握在共点力作用下物体的平衡条件.
3.知道如何用实验验证共点力作用下的物体的平衡条件.
4.应用共点力的平衡条件解决具体问题.
过程与方法
1.正确判断物体的运动状态,培养学生的观察和鉴别能力.
2.进一步培养学生分析物体受力的能力.
3.应用平衡条件解决实际问题的能力.
情感态度与价值观
1.了解运动和静止的相对性,培养学生的辩证唯物主义观点.
2.通过对周围处于静止状态的物体的观察和实验,总结出力的平衡条件,再用这个理论来解决和处理实际问题,使学生树立正确的认识观.
通过对物体受力分析图的绘画,使学生了解到物理学中的对称美.
教学设计
教学重点 1.共点力的平衡条件.
2.熟练运用共点力的平衡条件,解决平衡状态下有关力的计算.
3.进一步熟练受力分析的方法.
教学难点 1.物体的受力分析.
2.物体在什么条件下,可以认为是受到共点力作用?
3.物体受到三个不在一条直线上的力作用而处于平衡状态时,这三个力一定共点.
教具准备 投影仪、投影片.
课时安排 1课时
教学过程
导入新课式
1.用投影片出示复合题:
(1)如果一个物体能够保持_________或_________,我们就说物体处于平衡状态.
(2)当物体处于平衡状态时:
a.物体所受各个力的合力等于_________,这就是物体在共点力作用下的平衡条件.
b.它所受的某一个力与它所受的其余外力的合力关系是_________.
2.学生回答问题后,教师进行评价和纠正.
3.引入:本节课我们来运用共点力的平衡条件求解一些实际问题.
推进新课
1.共点力作用下物体的平衡条件的应用举例:
用投影片出示例题1:
[例题剖析1]如图5-4-1所示.细线的一端固定于A点,线的中点挂一质量为m的物体,另一端B用手拉住,当AO与竖直方向成θ角,OB沿水平方向时,AO及BO对O点的拉力分别是多大?
图5-4-1
解:先以物体m为研究对象,它受到两个力,即重力和悬线的拉力,因为物体处于平衡状态,所以悬线中的拉力大小为F=mg.
再取O点为研究对象,该点受三个力的作用,即AO对O点的拉力F1、BO对O点的拉力F2、悬线对O点的拉力F,如图5-4-2所示:
图5-4-2 图5-4-3
a.用力的分解法求解:
将F=mg沿F1和F2的反方向分解,得到
F′=mgtanθ;F″=mg/cosθ,
得到F1=mg/cosθ;F2=mgtanθ
b.用正交分解合成法求解:
建立平面直角坐标系
由Fx合=0及Fy合=0得到:
解得:F1=mg/cosθ F2=mgtanθ
2.结合例题总结求解共点力作用下平衡问题的解题步骤:
(1)确定研究对象;
(2)对研究对象进行受力分析,并画受力图;
(3)据物体的受力和已知条件,采用力的合成、分解、图解、正交分解法,确定解题方法;
(4)解方程,进行讨论和计算.
3.学生用上述方法求解下面例题,并抽查部分同学的答案在投影仪上进行评析.
[例题剖析2]如图5-4-4所示,两物体重分别为G1、G2,两弹簧劲度系数分别为k1、k2,弹簧两端与物体和地面相连.用竖直向上的力缓慢向上拉G2,最后平衡时拉力F=G1+2G2.求该过程系统重力势能的增量.
图5-4-4
解:关键是搞清两个物体高度的增量Δh1和Δh2跟初、末状态两根弹簧的形变量Δx1、Δx2、Δx1′、Δx2′间的关系.
无拉力F时:Δx1=(G1+G2)/k1,Δx2=G2/k2,(Δx1、Δx2为压缩量)
加拉力F时:Δx1′=G2/k1,Δx2′=(G1+G2)/k2,(Δx1′、Δx2′为伸长量)
而Δh1=Δx1+Δx1′,Δh2=(Δx1′+Δx2′)+(Δx1+Δx2)
系统重力势能的增量ΔEp=G1·Δh1+G2·Δh2
整理后可得:ΔEp=(G1+2G2)()
4.讲解有关斜面问题的处理方法
[例题剖析3]如图5-4-5所示,将重力为G的物体A放在倾角θ的斜面上,物体与斜面间的动摩擦因数为μ,那么对A施加一个多大的水平力F1,可使物体沿斜面匀速上滑?
分析本题:
图5-4-5
a.定物体A为研究对象
b.对物体A进行受力分析:
物体A共受四个力的作用:竖直向下的重力G、水平向右的力F1、垂直于斜面斜向上方的支持力F2、平行于斜面向下的滑动摩擦力F3,其中G和F1是已知的.由滑动摩擦定律F3=μF2可求得F2和F3,就可以求出μ.
c.画出物体的受力图如图5-4-6.
d.本题采用正交分解法:
图5-4-6
对于斜面,常取平行于斜面的方向为x轴,垂直于斜面的方向为y轴,将力沿这两个方向分解,应用平衡条件求解:
e.用投影片展示本题的解题过程:
解:取平行于斜面的方向为x轴,垂直于斜面的方向为y轴,分别在这两个方向上应用平衡条件求解,由平衡条件可知,在这两个方向上的合力Fx合和Fy合应分别等于零,即
Fx合=F3-F1cosθ+Gsinθ=0
Fy合=F2-F1sinθ-Gcosθ=0
并且F3=F2·μ
解得:F1=.
5.巩固训练
如图5-4-7所示,重为G=10 N的小球在竖直挡板作用下静止在倾角为θ=30°的光滑斜面上,已知挡板也是光滑的,求:
图5-4-7
(1)挡板对小球弹力的大小;
(2)斜面对小球弹力的大小.
课堂小结
本节课我们主要学习了以下几点:
1.应用共点力平衡条件解题时常用的方法——力的合成法、力的分解法、正交分解法.
2.解共点力作用下物体平衡问题的一般步骤:
(1)确定研究对象;
(2)对所选研究对象进行受力分析,并画出受力示意图;
(3)分析研究对象是否处于平衡状态;
(4)运用平衡条件,选用适当方法,列出平衡方程求解.
布置作业
练习1.如图5-4-8所示,一个半球形的碗放在桌面上,碗口水平,碗的内表面及碗口是光滑的.一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°.两小球的质量比为(A)
图5-4-8
A. B. C. D.
练习2.如图5-4-9所示,人重600 N,木板重400 N,人与木板、木板与地面间的动摩擦因数皆为0.2.现在人用水平力拉绳,使他与木块一起向右匀速运动,则(BC)
图5-4-9
A.人拉绳的力是200 N B.人拉绳的力是100 N
C.人的脚给木块摩擦力向右 D.人的脚给木块摩擦力向左
练习3.如图5-4-10所示,两个完全相同的小球,重力大小为G,两物体与地面间的动摩擦因数均为μ,一根轻绳的两端固定在两个球上,在绳的中点施加一个竖直向上的拉力,当绳被拉直后,两段绳的夹角为θ.求当F至少为多大时,两球将会发生相对滑动?(F=)
图5-4-10
练习4.如图5-4-11所示,两个固定的光滑硬杆OA与OB,夹角为θ,各套一轻环C、D,且C、D用细绳相连.现在用一水平恒力F沿OB方向拉环D,当两环平衡时,绳子的拉力是多大 (F/sinθ)
图5-4-11 图5-4-12
练习5.如图5-4-12所示,均匀杆AB重为G,A端用细绳吊在O点,在B端加一水平力F,使AB静止,此时杆与水平方向夹角为α,细绳与竖直方向成θ角.则(B)
A.拉力F一定大于G B.绳子拉力T一定大于G
C.AB杆与水平夹角α必小于θ D.F足够大时细绳可在水平方向上
板书设计
共点力平衡条件的应用
活动与探究
观察高压电线的塔架有何特点.
w.w.w.k.s.5.u.c.o.m
www.
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
- 第1章 绪论
- 物理学与自然规律
- 物理学与社会发展
- 怎样学习物理学
- 高中物理教材特点
- 第2章 运动的描述
- 导入 认识运动
- 第1节 运动、空间和时间
- 第2节 质点和位移
- 第3节 速度和加速度
- 第3章 匀变速直线运动的研究
- 导入 速度的变化
- 第1节 匀变速直线运动的规律
- 第2节 匀变速直线运动的实验探究
- 第3节 匀变速直线运动实例-自由落体运动
- 第4章 相互作用
- 导入 奇特的力现象
- 第1节 重力与重心
- 第2节 形变与弹力
- 第3节 摩擦力
- 第5章 力与平衡
- 导入 感悟平衡之美
- 第1节 力的合成
- 第2节 力的分解
- 第3节 力的平衡
- 第4节 平衡条件的应用
- 第6章 力与运动
- 导入 跨越时空的对话
- 第1节 牛顿第一定律
- 第2节 牛顿第二定律
- 第3节 牛顿第三定律
- 第4节 超重与失重
- 本章复习与测试
