陕西省西安市2017-2018学年高一下学期期末考试仿真卷(A卷)数学试卷(学生版)(必修三、必修四) Word版含答案
文档属性
| 名称 | 陕西省西安市2017-2018学年高一下学期期末考试仿真卷(A卷)数学试卷(学生版)(必修三、必修四) Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 331.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-23 21:23:26 | ||
图片预览



文档简介
2017-2018学年下学期高一期末考试仿真卷
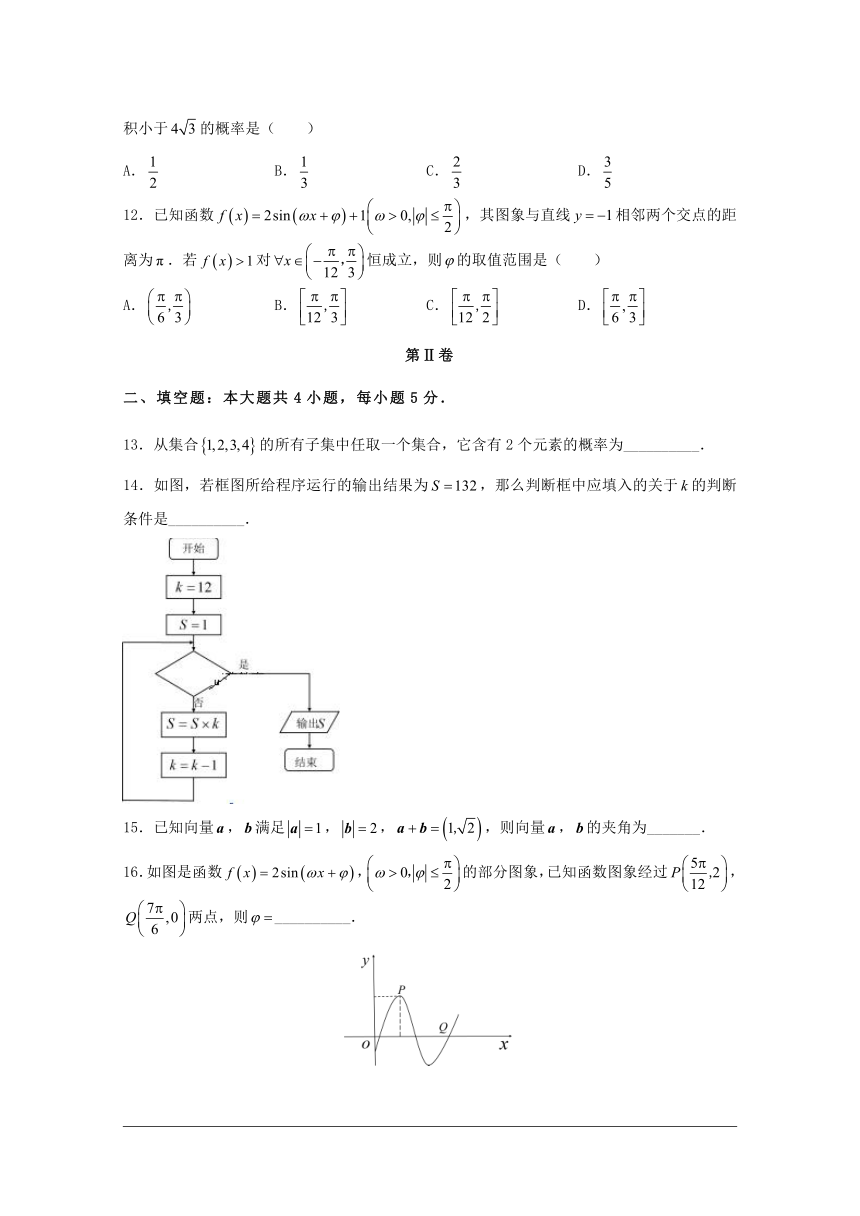
数学(A)
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某企业有职工人,其中高级职称人,中级职称人,一般职员人,现抽取人进行分层抽样,则各职称人数分别为( )
A.,, B.,, C.,, D.,,
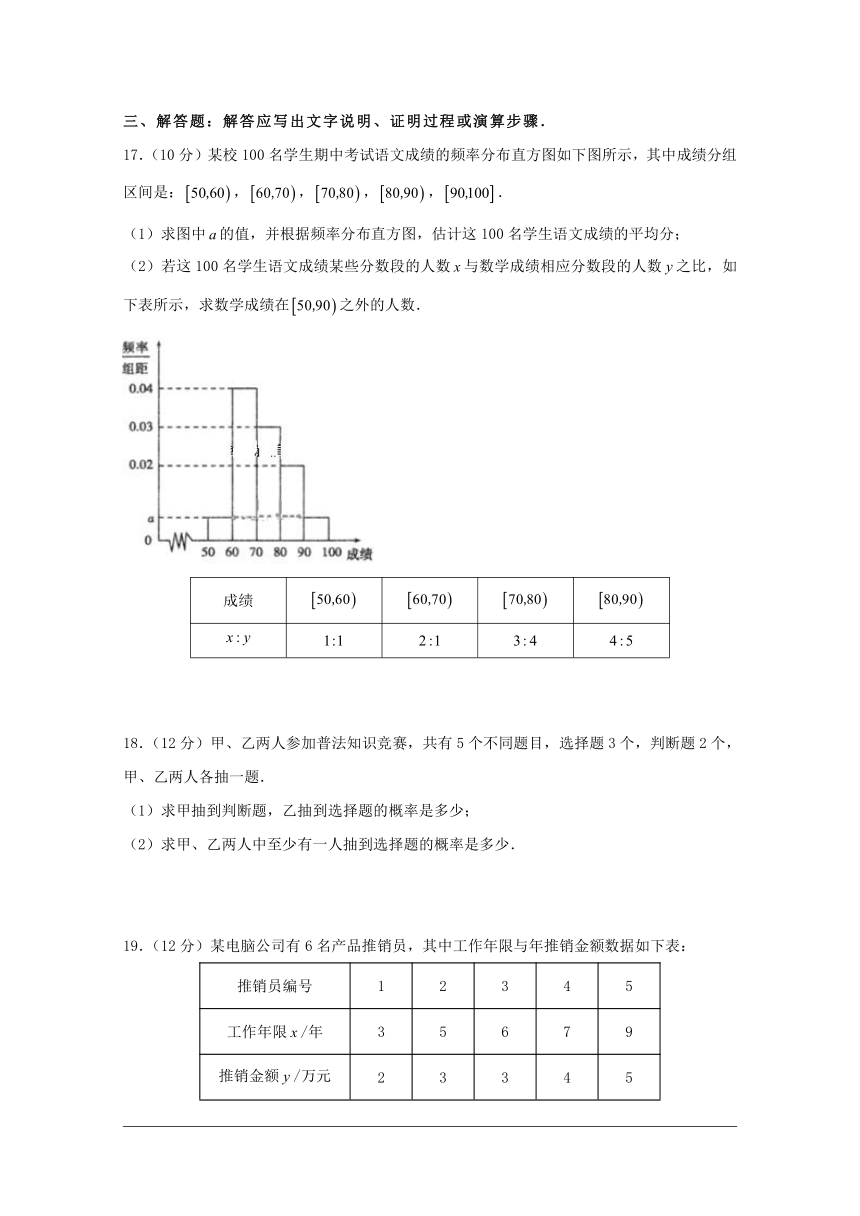
2.已知,则的值为( )
A. B. C. D.
3.已知向量,,且,则( )
A. B. C. D.5
4.( )
A. B. C. D.
5.五四青年节活动中,高三(1)、(2)班都进行了3场知识辩论赛,比赛得分情况的茎叶图如图所示(单位:分),其中高三(2)班得分有一个数字被污损,无法确认,假设这个数字具有随机性,那么高三(2)班的平均得分大于高三(1)班的平均得分的概率为( )
A. B. C. D.
6.执行完如图的程序框图后,与应满足的关系为( )
A. B. C. D.
7.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,……,699,700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第6个样本编号是( )
32211834297864540732524206443812234356773578905642
84421253313457860736253007328623457889072368960804
32567808436789535577348994837522535578324577892345
A.623 B.328 C.253 D.007
8.将函数的图像向右平移个单位长度,得到函数的图像,若在上为增函数,则的最大值为( )
A.3 B.2 C. D.
9.设,为正三角形中边上的两个三等分点,且,则( )
A. B. C. D.
10.若,,,,则等于( )
A. B. C. D.
11. 中,,,,在线段上任取一点,则的面积小于的概率是( )
A. B. C. D.
12.已知函数,其图象与直线相邻两个交点的距离为.若对恒成立,则的取值范围是( )
A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分.
13.从集合的所有子集中任取一个集合,它含有2个元素的概率为__________.
14.如图,若框图所给程序运行的输出结果为,那么判断框中应填入的关于的判断条件是__________.
15.已知向量,满足,,,则向量,的夹角为_______.
16.如图是函数,的部分图象,已知函数图象经过,两点,则__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(10分)某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是:,,,,.
(1)求图中的值,并根据频率分布直方图,估计这100名学生语文成绩的平均分;
(2)若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数之比,如下表所示,求数学成绩在之外的人数.
成绩
18.(12分)甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)求甲抽到判断题,乙抽到选择题的概率是多少;
(2)求甲、乙两人中至少有一人抽到选择题的概率是多少.
19.(12分)某电脑公司有6名产品推销员,其中工作年限与年推销金额数据如下表:
推销员编号
1
2
3
4
5
工作年限/年
3
5
6
7
9
推销金额/万元
2
3
3
4
5
(1)请画出上表数据的散点图;
(2)求年推销金额关于工作年限的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
,.
20.(12分)设,,满足,及.
(1)求与的夹角;
(2)求的值.
21.(12分)已知,.
(1)若,且,求的值;
(2)设,,若方程恰有两个不同的解,求实数的取值范围.
22.(12分)已知函数,.
(1)求函数的最小正周期;
(2)若,求函数的最大值及其相应的值.
2017-2018学年下学期高一期末考试仿真卷
数学(A)答案
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】由题意可得抽样比为,所以高级职称人,
中级职称人,一般职员人,故选B.
2.【答案】D
【解析】由诱导公式可得,
则.故选D.
3.【答案】B
【解析】根据题意可得,可得,
所以,从而可求得,故选B.
4.【答案】A
【解析】
,故选A.
5.【答案】D
【解析】由径叶图可得高三(1)班的平均分为,高三(2)的平均分为,由,得,又,所以可取6,7,8,9,概率为,故选D.
6.【答案】B
【解析】根据题中所给的程序框图,在执行完后,不难算出输出的,的值分别是,,将两个量分别对各个选项逐一验证,可以发现,故选B.
7.【答案】A
【解析】从第5行第6列开始向右读取数据,第一个数为253,第二个数是313,第三个数是457,下一个数是860,不符合要求,下一个数是736,不符合要求,下一个是253,重复,
第四个是007,第五个是328,第六个是623,故选A.
8.【答案】B
【解析】由题意可得,
当时,,由于,故函数在上不是增函数,
当时,,由于,故函数在上是增函数.
故选B.
9.【答案】C
【解析】
,,,是边的两个三等分点,
,
.故选C.
10.【答案】C
【解析】由题意得,故,
因为,所以,所以,
所以
.故选C.
11.【答案】C
【解析】由,,可得,
,,,
的面积小于的概率为.故选C.
12.【答案】D
【解析】函数,其图象与直线相邻两个交点的距离为,故函数的周期为,,,
若对恒成立,即当时,恒成立, 故有,,求得,,
又,.故选D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】由题意得,集合有个子集,含有2个元素的集合共有种,
故含有2个元素的概率为.
14.【答案】或
【解析】按照程序框图执行如下:,;,;,,
因为输出132,故此时判断条件应为或.
15.【答案】
【解析】由题意,,,可得,所以,又因为,且,所以,
所以向量,的夹角为.
16.【答案】
【解析】由图象可得,,,.
根据题意得,解得.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1),平均分73;(2)10.
【解析】(1)依题意,得,解得,
这100名学生语文成绩的平均分为分.
(2)数学成绩在的人数为,
数学成绩在的人数为,
数学成绩在的人数为,
数学成绩在的人数为,
所以数学成绩在之外的人数为.
18.【答案】(1);(2).
【解析】5个不同题目,甲、乙两人各抽一题,共有20种情况,把3个选择题记为、、,2个判断题记为、.“甲抽到选择题,乙抽到判断题”的情况有:,,,,,,共6种;“甲抽到判断题,乙抽到选择题”的情况有:,,,,,,共6种;“甲、乙都抽到选择题”的情况有:,,,,,,共6种;“甲、乙都抽到判断题”的情况有:,,共2种.
(1)“甲抽到选择题,乙轴到判断题”的概率为,
(2)“甲、乙两人都抽到判断题”的概率为,故“甲、乙两人至少有一人抽到选择题”的概率为.
19.【答案】(1)散点图见解析;(2);(3)万元.
【解析】(1)散点图如图所示:
(2)由(1)知与具有线性相关关系.,,
,,,.
年推销金额关于工作年限的线性回归方程为.
(3)由(2)知,当时,.可以估计第6名推销员的年推销金额为万元.
20.【答案】(1);(2).
【解析】(1)平方得,,
,.
(2).
21.【答案】(1);(2).
【解析】(1),,
即,,
,,
,.
(2),当时,,
结合函数的图象可看出有两个交点,实数的取值范围是.
22.【答案】(1);(2),.
【解析】(1),
所以.
(2),,
当即时,函数取到最大值为.
数学(A)
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.某企业有职工人,其中高级职称人,中级职称人,一般职员人,现抽取人进行分层抽样,则各职称人数分别为( )
A.,, B.,, C.,, D.,,
2.已知,则的值为( )
A. B. C. D.
3.已知向量,,且,则( )
A. B. C. D.5
4.( )
A. B. C. D.
5.五四青年节活动中,高三(1)、(2)班都进行了3场知识辩论赛,比赛得分情况的茎叶图如图所示(单位:分),其中高三(2)班得分有一个数字被污损,无法确认,假设这个数字具有随机性,那么高三(2)班的平均得分大于高三(1)班的平均得分的概率为( )
A. B. C. D.
6.执行完如图的程序框图后,与应满足的关系为( )
A. B. C. D.
7.某工厂利用随机数表对生产的700个零件进行抽样测试,先将700个零件进行编号,001,002,……,699,700.从中抽取70个样本,下图提供随机数表的第4行到第6行,若从表中第5行第6列开始向右读取数据,则得到的第6个样本编号是( )
32211834297864540732524206443812234356773578905642
84421253313457860736253007328623457889072368960804
32567808436789535577348994837522535578324577892345
A.623 B.328 C.253 D.007
8.将函数的图像向右平移个单位长度,得到函数的图像,若在上为增函数,则的最大值为( )
A.3 B.2 C. D.
9.设,为正三角形中边上的两个三等分点,且,则( )
A. B. C. D.
10.若,,,,则等于( )
A. B. C. D.
11. 中,,,,在线段上任取一点,则的面积小于的概率是( )
A. B. C. D.
12.已知函数,其图象与直线相邻两个交点的距离为.若对恒成立,则的取值范围是( )
A. B. C. D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分.
13.从集合的所有子集中任取一个集合,它含有2个元素的概率为__________.
14.如图,若框图所给程序运行的输出结果为,那么判断框中应填入的关于的判断条件是__________.
15.已知向量,满足,,,则向量,的夹角为_______.
16.如图是函数,的部分图象,已知函数图象经过,两点,则__________.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.(10分)某校100名学生期中考试语文成绩的频率分布直方图如下图所示,其中成绩分组区间是:,,,,.
(1)求图中的值,并根据频率分布直方图,估计这100名学生语文成绩的平均分;
(2)若这100名学生语文成绩某些分数段的人数与数学成绩相应分数段的人数之比,如下表所示,求数学成绩在之外的人数.
成绩
18.(12分)甲、乙两人参加普法知识竞赛,共有5个不同题目,选择题3个,判断题2个,甲、乙两人各抽一题.
(1)求甲抽到判断题,乙抽到选择题的概率是多少;
(2)求甲、乙两人中至少有一人抽到选择题的概率是多少.
19.(12分)某电脑公司有6名产品推销员,其中工作年限与年推销金额数据如下表:
推销员编号
1
2
3
4
5
工作年限/年
3
5
6
7
9
推销金额/万元
2
3
3
4
5
(1)请画出上表数据的散点图;
(2)求年推销金额关于工作年限的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
,.
20.(12分)设,,满足,及.
(1)求与的夹角;
(2)求的值.
21.(12分)已知,.
(1)若,且,求的值;
(2)设,,若方程恰有两个不同的解,求实数的取值范围.
22.(12分)已知函数,.
(1)求函数的最小正周期;
(2)若,求函数的最大值及其相应的值.
2017-2018学年下学期高一期末考试仿真卷
数学(A)答案
第Ⅰ卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】由题意可得抽样比为,所以高级职称人,
中级职称人,一般职员人,故选B.
2.【答案】D
【解析】由诱导公式可得,
则.故选D.
3.【答案】B
【解析】根据题意可得,可得,
所以,从而可求得,故选B.
4.【答案】A
【解析】
,故选A.
5.【答案】D
【解析】由径叶图可得高三(1)班的平均分为,高三(2)的平均分为,由,得,又,所以可取6,7,8,9,概率为,故选D.
6.【答案】B
【解析】根据题中所给的程序框图,在执行完后,不难算出输出的,的值分别是,,将两个量分别对各个选项逐一验证,可以发现,故选B.
7.【答案】A
【解析】从第5行第6列开始向右读取数据,第一个数为253,第二个数是313,第三个数是457,下一个数是860,不符合要求,下一个数是736,不符合要求,下一个是253,重复,
第四个是007,第五个是328,第六个是623,故选A.
8.【答案】B
【解析】由题意可得,
当时,,由于,故函数在上不是增函数,
当时,,由于,故函数在上是增函数.
故选B.
9.【答案】C
【解析】
,,,是边的两个三等分点,
,
.故选C.
10.【答案】C
【解析】由题意得,故,
因为,所以,所以,
所以
.故选C.
11.【答案】C
【解析】由,,可得,
,,,
的面积小于的概率为.故选C.
12.【答案】D
【解析】函数,其图象与直线相邻两个交点的距离为,故函数的周期为,,,
若对恒成立,即当时,恒成立, 故有,,求得,,
又,.故选D.
第Ⅱ卷
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】由题意得,集合有个子集,含有2个元素的集合共有种,
故含有2个元素的概率为.
14.【答案】或
【解析】按照程序框图执行如下:,;,;,,
因为输出132,故此时判断条件应为或.
15.【答案】
【解析】由题意,,,可得,所以,又因为,且,所以,
所以向量,的夹角为.
16.【答案】
【解析】由图象可得,,,.
根据题意得,解得.
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.【答案】(1),平均分73;(2)10.
【解析】(1)依题意,得,解得,
这100名学生语文成绩的平均分为分.
(2)数学成绩在的人数为,
数学成绩在的人数为,
数学成绩在的人数为,
数学成绩在的人数为,
所以数学成绩在之外的人数为.
18.【答案】(1);(2).
【解析】5个不同题目,甲、乙两人各抽一题,共有20种情况,把3个选择题记为、、,2个判断题记为、.“甲抽到选择题,乙抽到判断题”的情况有:,,,,,,共6种;“甲抽到判断题,乙抽到选择题”的情况有:,,,,,,共6种;“甲、乙都抽到选择题”的情况有:,,,,,,共6种;“甲、乙都抽到判断题”的情况有:,,共2种.
(1)“甲抽到选择题,乙轴到判断题”的概率为,
(2)“甲、乙两人都抽到判断题”的概率为,故“甲、乙两人至少有一人抽到选择题”的概率为.
19.【答案】(1)散点图见解析;(2);(3)万元.
【解析】(1)散点图如图所示:
(2)由(1)知与具有线性相关关系.,,
,,,.
年推销金额关于工作年限的线性回归方程为.
(3)由(2)知,当时,.可以估计第6名推销员的年推销金额为万元.
20.【答案】(1);(2).
【解析】(1)平方得,,
,.
(2).
21.【答案】(1);(2).
【解析】(1),,
即,,
,,
,.
(2),当时,,
结合函数的图象可看出有两个交点,实数的取值范围是.
22.【答案】(1);(2),.
【解析】(1),
所以.
(2),,
当即时,函数取到最大值为.
同课章节目录
