21.2 二次函数的图象和性质(1)同步作业
文档属性
| 名称 | 21.2 二次函数的图象和性质(1)同步作业 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-23 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
21.2 二次函数的图象和性质(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.已知点(-1,2)在二次函数y=ax2的图象上,那么a的值是( )
A. 1 B. 2 C. EMBED Equation.DSMT4 D. -
2.函数y=ax2(a≠0)的图象经过点(a,8),则a的值为( )
A. ±2 B. -2 C. 2 D. 3
3.抛物线y= EMBED Equation.DSMT4 x2,y=4x2,y=-2x2的图像中,开口最大的是( )
A. y=x2 B. y=4x2 C. y=-2x2 D. 无法确定
4.如图,四个二次函数的图象中,分别对应的是:①;②;③;④,则的大小关系为( )
A. B. C. D.
5.抛物线y=3x 2 的顶点坐标是( )
A. (3,0) B. (0,3) C. (0,0) D. (1,3)
6.若抛物线经过点P(1,-3),则此抛物线也经过点( )
A. P B. P C. P (1,3) D. P
7.在同一坐标系中,抛物线, , 的共同特点是( )
A. 关于y轴对称,开口向上 B. 关于y轴对称,y随x增大而减小
C. 关于y轴对称,y随x增大而增大 D. 关于y轴对称,顶点在原点
8.已知点(-2,),(0,),(1,)都在函数的图象上,则( )
A. >> B. >> C. >> D. >>
9.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A. y110.下列说法中错误的是( )
A. 在函数中,当时有最大值
B. 在函数中,当时随的增大而增大
C. 抛物线,,中,抛物线的开口最小,抛物线的开口最大
D. 不论是正数还是负数,抛物线的顶点都是坐标原点
11.如图,在平面直角坐标系中,A(1,2),B(1,-1),C(2,2),抛物线y=ax2(a≠0)经过△ABC区域(包括边界),则a的取值范围是( )
A. a≤-1或a≥2 B. ≤a≤2 C. -1≤a<0或1<a≤ D. -1≤a<0或0<a≤2
二、填空题
12.已知二次函数的图象开口向下,则m的取值范围是______ .
13.写出一个开口向上,顶点是坐标原点的二次函数的解析式:___________.
14.某抛物线有以下性质:①开口向下;②对称轴是y轴;③与x轴不相交;④最高点是原点.其中y=﹣2x2具有的性质是_____.(填序号)
15.抛物线y=2x2的顶点,坐标为______,对称轴是______.当x______时,y随x增大而减小;当x______时,y随x增大而增大;当x=______时,y有最______值是______.
16.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y= EMBED Equation.DSMT4 x2与y=–x2的图象,则阴影部分的面积是__________.
17.若抛物线y=ax2经过点A (,-9),则其解析式为_______________。
18.已知二次函数y甲=mx2和y乙=nx2,对任意给定一个x值都有y甲≥y乙,关于m,n的关系正确的是_____(填序号).①m0,n<0 ③m<0,n>0 ④m>n>0
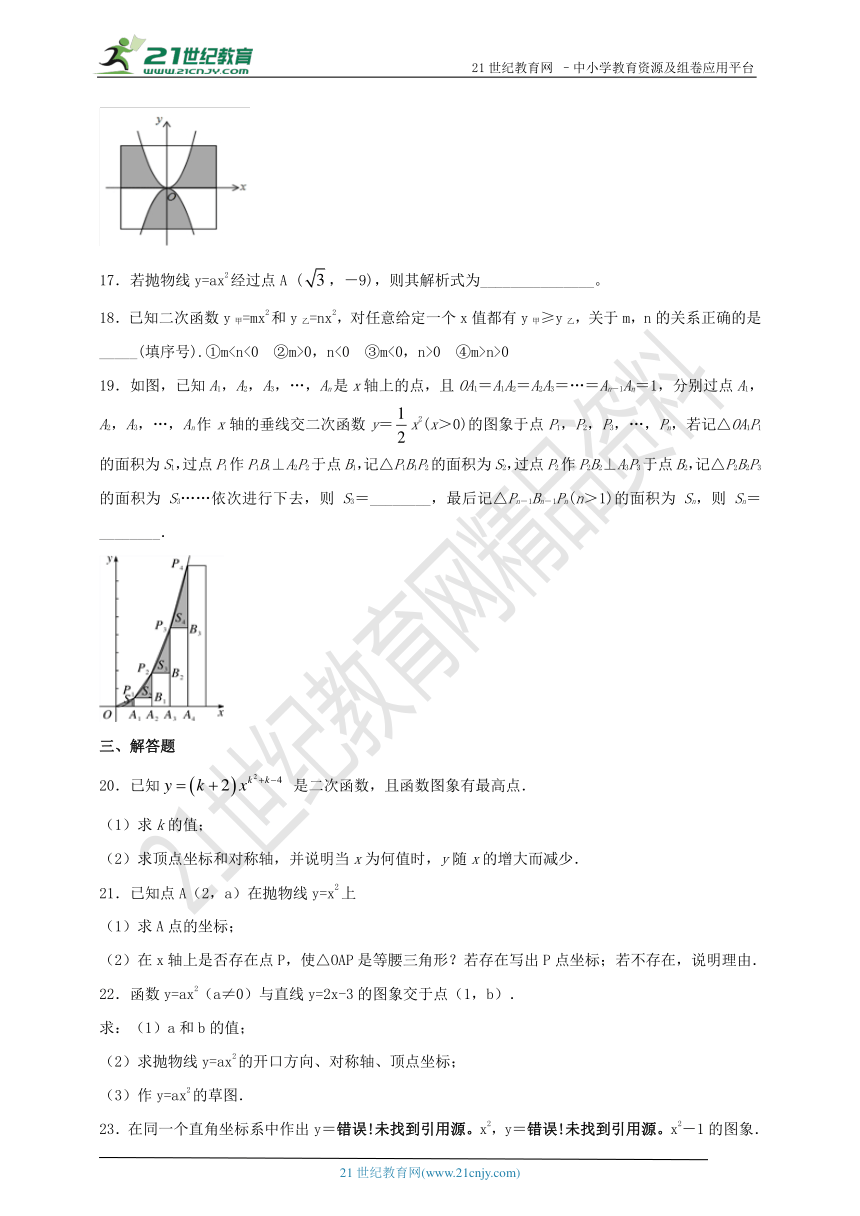
19.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
三、解答题
20.已知 是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减少.
21.已知点A(2,a)在抛物线y=x2上
(1)求A点的坐标;
(2)在x轴上是否存在点P,使△OAP是等腰三角形?若存在写出P点坐标;若不存在,说明理由.
22.函数y=ax2(a≠0)与直线y=2x-3的图象交于点(1,b).
求:(1)a和b的值;
(2)求抛物线y=ax2的开口方向、对称轴、顶点坐标;
(3)作y=ax2的草图.
23.在同一个直角坐标系中作出y=x2,y=x2-1的图象.
(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=x2-1与抛物线y=x2有什么关系?
24.已知抛物线y=ax2经过点(1,3).
(1)求a的值;
(2)当x=3时,求y的值;
(3)说出此二次函数的三条性质.
25.如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB.
参考答案
1.B
【解析】∵点(-1,2)在二次函数的图象上,
∴,解得: .
故选B.
2.C
【解析】把点(a,8)代入:y=ax2得:a3=8,解得:a=2.
故选C.
3.A
【解析】分别写出二次项系数的绝对值并比较大小.||<|2|<|4|,根据性质可知开口大小.
解:当x=1时,三条抛物线的对应点是(1, )(1,4),(1,-2),
因为||<|-2|<|4|,
所以抛物线y=x2开口最大.
故选A.
4.A
【解析】由二次函数中,“当二次项系数为正时,图象开口向上,当二次项系数为负时,图象开口向下”结合“二次项系数的绝对值越大,图象的开口越大”分析可得:
.
故选A.
点睛:(1)二次函数的图象的开口方向由“的符号”确定,当时,图象的开口向上,当时,图象的开口向下;(2)二次函数的图象的开口大小由的大小确定,当越大时,图象的开口越小.
5.C
【解析】试题解析:∵抛物线y=3x2,
∴抛物线y=3x2的顶点坐标是:(0,0),
故选C.
6.D
【解析】
试题解析:∵将点P(1,-3)代入y=ax2得a=-3,
∴y=-3x2,
将四个点坐标分别代入解析式可知,当x=-1时,y=-3,即D选项正确,其他三个选项均不成立.
故选D.
7.D
【解析】解:∵函数y=2x2,y=x2,y=x2中,a取值范围分别为:a>0,a>0,a<0,∴抛物线的开口方向分别为:向上、向上、向下,即开口方向不同;
由函数y=2x2,y=x2,y=x2的解析式可知:顶点坐标都为(0,0);
∴他们共同的特点是都关于y轴对称,抛物线的顶点都是原点.
故选D.
8.A
【解析】函数的图象的对称轴是y轴,顶点是原点,开口向上,所以离原点越远,函数值就越大.
因为|-2|>1>0,所以y1>y3>y2.
故选A.
9.C
【解析】由a<-1可得a-1<a<a+1<0,又因点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,在对称轴的左侧,y随x的增大而减小,所以 y310.C
【解析】A.在函数y=-x2中,当x=0时y有最大值0,正确,
因为:此抛物线顶点坐标在原点,开口方向向下,故当x=0时y有最大值0;
B.在函数y=2x2中,当x>0时y随x的增大而增大,正确;
因为此抛物线对称轴为y轴,开口方向向上,则x>0时y随x的增大而增大;
C.抛物线y=2x2,y=-x2,y=-x2中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大;错误;
根据绝对值越大开口越小,可得抛物线y=2x2的开口最小,抛物线y=-x2的开口最大;
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点,正确,
因为y=ax2(a≠0)的顶点始终为原点.
【点睛】本题主要考查了二次函数的性质,解题的关键是熟练掌握顶点坐标,对称轴以及开口方向等知识,此题难度不大.
11.D
【解析】分析:分a<0和a>0两种情况,确定开口最小经过的点,代入解析式求出a的取值范围即可.
详解:若a<0,则抛物线开口向下,开口最小过点B(1,-1)
∴-1=a×12
∴a=-1
∴-1≤a<0
若a>0,则抛物线开口向上,开口最小过点A(1,2)
∴2=a×12
∴a=2
∴0∴a的取值范围是-1≤a<0或0故选B.
点睛:本题考查了二次函数的图象,有一定难度,进行分类讨论是解题的关键.
12.m<2
【解析】∵二次函数的图象开口向下,
∴m-2<0,解得:m<2.
故答案为:m<2.
13.y=2x2
【解析】图象的顶点在原点,开口向上的二次函数很多,如: .
14.①②④.
【解析】y=-2x2开口向下,对称轴是y轴,与x轴有一个交点,最高点是原点.
故答案为①②④.
点睛:掌握二次函数的图像及性质.
15. (0,0) y轴 ≤0 >0 0 小 0.
【解析】解:抛物线y=2x2的顶点,坐标为(0,0),对称轴是y轴.当x≤0时,y随x增大而减小;当x>0时,y随x增大而增大;当x=0时,y有最小值是0.
故答案为: (0,0) ; y轴 ; ≤0 ;>0 ; 0 ; 小; 0.
16.8
【解析】函数y=x2与y=–x2的图象关于x轴对称,又因正方形的边长为4,以正方形中心为原点建立平面直角坐标系,所以阴影部分的面积为正方形面积的一半,即4×4×=8.
点睛:本题考查了抛物线的性质,熟知与的图象关于x轴对称是解决问题的关键.
17.y=-3x2
【解析】把点A代入: 得, ,解得: ,
∴该抛物线的解析式为: .
18.②④
【解析】∵x2一定不小于0,则由条件“对应任意给定的x的值,都有y甲 y乙”可知:存在以下3种情况:
(1)若y甲和y乙都为正数,则m>0,n>0且m>n,即m>n>0;
(2)若y甲为正数,y乙为负数,则m>0,n<0;
(3)若都为负数时,则n<m<0;
∴关于m,n的关系正确的是② 、④ .
19.
【解析】当x=1时,y=x2=,则P1(1, ),所以S1=×1×=;
当x=2时,y=x2=2,则P2(2,2),所以S2=×1×(2-)= ;
当x=3时,y=x2=,则P3(3, ),所以S3=×1×(-2)=,
同样方法可得S4=,
所以Sn=.
故答案是: , .
【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了三角形面积公式.
20.(1)k=﹣3;(2)当k=﹣3时,y=﹣x2顶点坐标(0,0),对称轴为y轴,当x>0时,y随x的增大而减少.
【解析】试题分析:(1)根据二次函数的定义得出k2+k﹣4=2,再利用函数图象有最高点,得出k+2<0,即可得出k的值;
(2)利用(1)中k的值得出二次函数的解析式,利用形如y=ax2(a≠0)的二次函数顶点坐标为(0,0),对称轴是y轴即可得出答案.
试题解析:解:(1)∵是二次函数,∴k2+k﹣4=2且k+2≠0,解得k=﹣3或k=2.∵函数有最高点,∴抛物线的开口向下,∴k+2<0,解得k<﹣2,∴k=﹣3;
(2)当k=﹣3时,二次函数为y=﹣x2,顶点坐标为(0,0),对称轴为y轴,当x>0时,y随x的增大而减少.
21.(1)A点的坐标为:(2,4);(2)(2,0),(﹣2,0),(4,0),(5,0).
【解析】试题分析:(1)直接将A点代入解析式求出即可A点坐标即可;
(2)分别根据以O为顶点时,以A为顶点时,以P为顶点时求出符合题意的点的坐标即可.
试题解析:(1)∵点A(2,a)在抛物线y=x2上,∴a=22=4,
∴A点的坐标为:(2,4);
(2)如图所示:以O为顶点时,AO=P1O=2或AO=AP2=2
∴点P坐标:(2,0),(﹣2,0),以A为顶点时,AO=OP,
∴点P坐标:(4,0);以P为顶点时,OP′=AP′,
∴AE2+P′E2=P′A2,设AP′=x则42+(x﹣2)2=x2,解得:x=5,
∴点P坐标:(5,0),
综上所述使△OAP是等腰三角形则P点坐标为:(2,0),(﹣2,0),(4,0),(5,0).
22.(1)a=-1(2)y轴,(0,0)(3)图像见解析
【解析】试题分析:
(1)把点(1,b)代入y=2x-3中解得b的值,再把(1,b)代入y=ax2,中可解得a的值;
(2)由(1)中所求得的a的值,可得y=ax2的解析式,从而可确定抛物线y=ax2的开口方向,对称轴和顶点坐标;
(3)根据(2)中求得的抛物线y=ax2的开口方向、对称轴和顶点坐标可画出其草图.
试题解析:
(1)把(1,b)代入直线y=2x-3中,得b=2-3=-1,
把点(1,-1)代入y=ax2中,得a=-1;
(2)∵在y=-x2中,a=-1<0,
∴抛物线开口向下;
抛物线y=ax2的对称轴为y轴,顶点坐标为(0,0);
(3)作函数y=ax2的草图如下:
视频 ( http: / / qbm. / console / / media / Eav5S7TOlADNNq_QNVJsJ8azAU8bCp1TYsIBEk3JtT95_z9LGst1Vy9zKNNicDiideT_EHL6dJgUcbysgicX88dr8zlTjoBCtwREOpVZWepBuuU34LehdRLK01928wssd4PzhMfR9yrGqYq9wLNHJg )
23.见解析
【解析】试题分析:观察图像结合函数表达式可以得到两个函数开口向上,对称轴也都是y轴,顶点坐标分别是(0,0),(0,-1);根据二次函数的性质及图像知道抛物线y=x2-1与抛物线y=x2形状相同,对称轴相同,但是位置不同,开口方向也相同,所以可以得到抛物线y=x2-1可由抛物线y=x2向下平移1个单位长度得到的。
解:如图所示:
(1)抛物线y=x2开口向上,对称轴为y轴,顶点坐标(0,0);
抛物线y=x2-1开口向上,对称轴为y轴,顶点坐标(0,-1).
(2)抛物线y=x2-1可由抛物线y=x2向下平移1个单位长度得到.
24.(1) 3;(2) 27;(3)答案不唯一,
【解析】试题分析:抛物线y=ax2经过点(1,3),将点代入即可求得a=3,将x=3代入函数中求得y=27.二次函数的性质可以通过从开口方向,对称轴,顶点坐标,增减性等方面进行分析.
解:(1)∵抛物线y=ax2经过点(1,3),
∴a·1=3.∴a=3.
(2)把x=3代入抛物线y=3x2,得y=3×32=27.
(3)答案不唯一,如:抛物线的开口向上;坐标原点是抛物线的顶点;当x>0时,y随着x的增大而增大;抛物线的图象有最低点,当x=0时,y有最小值,是y=0等.
25.(1)y=﹣x+2,y=x2;(2)点C坐标为(﹣2,4);(3)3.
【解析】试题分析:(1)已知直线AB经过A(2,0),B(1,1),设直线表达式为y=kx+b,可求直线解析式;将B(1,1)代入抛物线y=ax2可求抛物线解析式;
(2)将(1)中所求的直线AB的解析式与抛物线y=ax2的解析式联立,得到方程组,解方程即可求出点C的坐标;
(3)已知A,B,C三点坐标,根据S△COB=S△AOC﹣S△OAB即可求△COB的面积.
试题解析:
(1)设直线表达式为y=kx+b.
∵A(2,0),B(1,1)都在y=kx+b的图象上,
∴,解得 ,,
∴直线AB的表达式为y=﹣x+2;
∵点B(1,1)在y=ax2的图象上,
∴a=1,其表达式为y=x2;
(2)由 ,解得 或,
∴点C坐标为(﹣2,4);
(3)S△COB=S△AOC﹣S△OAB=×2×4﹣×2×1=3.
【点睛】本题考查了二次函数的性质,利用待定系数法求一次函数、二次函数的解析式,三角形的面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
21.2 二次函数的图象和性质(1)同步作业
姓名:___________班级:___________考号:___________
一、选择题
1.已知点(-1,2)在二次函数y=ax2的图象上,那么a的值是( )
A. 1 B. 2 C. EMBED Equation.DSMT4 D. -
2.函数y=ax2(a≠0)的图象经过点(a,8),则a的值为( )
A. ±2 B. -2 C. 2 D. 3
3.抛物线y= EMBED Equation.DSMT4 x2,y=4x2,y=-2x2的图像中,开口最大的是( )
A. y=x2 B. y=4x2 C. y=-2x2 D. 无法确定
4.如图,四个二次函数的图象中,分别对应的是:①;②;③;④,则的大小关系为( )
A. B. C. D.
5.抛物线y=3x 2 的顶点坐标是( )
A. (3,0) B. (0,3) C. (0,0) D. (1,3)
6.若抛物线经过点P(1,-3),则此抛物线也经过点( )
A. P B. P C. P (1,3) D. P
7.在同一坐标系中,抛物线, , 的共同特点是( )
A. 关于y轴对称,开口向上 B. 关于y轴对称,y随x增大而减小
C. 关于y轴对称,y随x增大而增大 D. 关于y轴对称,顶点在原点
8.已知点(-2,),(0,),(1,)都在函数的图象上,则( )
A. >> B. >> C. >> D. >>
9.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,则( )
A. y1
A. 在函数中,当时有最大值
B. 在函数中,当时随的增大而增大
C. 抛物线,,中,抛物线的开口最小,抛物线的开口最大
D. 不论是正数还是负数,抛物线的顶点都是坐标原点
11.如图,在平面直角坐标系中,A(1,2),B(1,-1),C(2,2),抛物线y=ax2(a≠0)经过△ABC区域(包括边界),则a的取值范围是( )
A. a≤-1或a≥2 B. ≤a≤2 C. -1≤a<0或1<a≤ D. -1≤a<0或0<a≤2
二、填空题
12.已知二次函数的图象开口向下,则m的取值范围是______ .
13.写出一个开口向上,顶点是坐标原点的二次函数的解析式:___________.
14.某抛物线有以下性质:①开口向下;②对称轴是y轴;③与x轴不相交;④最高点是原点.其中y=﹣2x2具有的性质是_____.(填序号)
15.抛物线y=2x2的顶点,坐标为______,对称轴是______.当x______时,y随x增大而减小;当x______时,y随x增大而增大;当x=______时,y有最______值是______.
16.如图,正方形的边长为4,以正方形中心为原点建立平面直角坐标系,作出函数y= EMBED Equation.DSMT4 x2与y=–x2的图象,则阴影部分的面积是__________.
17.若抛物线y=ax2经过点A (,-9),则其解析式为_______________。
18.已知二次函数y甲=mx2和y乙=nx2,对任意给定一个x值都有y甲≥y乙,关于m,n的关系正确的是_____(填序号).①m
19.如图,已知A1,A2,A3,…,An是x轴上的点,且OA1=A1A2=A2A3=…=An-1An=1,分别过点A1,A2,A3,…,An作x轴的垂线交二次函数y=x2(x>0)的图象于点P1,P2,P3,…,Pn,若记△OA1P1的面积为S1,过点P1作P1B1⊥A2P2于点B1,记△P1B1P2的面积为S2,过点P2作P2B2⊥A3P3于点B2,记△P2B2P3的面积为S3……依次进行下去,则S3=________,最后记△Pn-1Bn-1Pn(n>1)的面积为Sn,则Sn=________.
三、解答题
20.已知 是二次函数,且函数图象有最高点.
(1)求k的值;
(2)求顶点坐标和对称轴,并说明当x为何值时,y随x的增大而减少.
21.已知点A(2,a)在抛物线y=x2上
(1)求A点的坐标;
(2)在x轴上是否存在点P,使△OAP是等腰三角形?若存在写出P点坐标;若不存在,说明理由.
22.函数y=ax2(a≠0)与直线y=2x-3的图象交于点(1,b).
求:(1)a和b的值;
(2)求抛物线y=ax2的开口方向、对称轴、顶点坐标;
(3)作y=ax2的草图.
23.在同一个直角坐标系中作出y=x2,y=x2-1的图象.
(1)分别指出它们的开口方向、对称轴以及顶点坐标;
(2)抛物线y=x2-1与抛物线y=x2有什么关系?
24.已知抛物线y=ax2经过点(1,3).
(1)求a的值;
(2)当x=3时,求y的值;
(3)说出此二次函数的三条性质.
25.如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).
(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB.
参考答案
1.B
【解析】∵点(-1,2)在二次函数的图象上,
∴,解得: .
故选B.
2.C
【解析】把点(a,8)代入:y=ax2得:a3=8,解得:a=2.
故选C.
3.A
【解析】分别写出二次项系数的绝对值并比较大小.||<|2|<|4|,根据性质可知开口大小.
解:当x=1时,三条抛物线的对应点是(1, )(1,4),(1,-2),
因为||<|-2|<|4|,
所以抛物线y=x2开口最大.
故选A.
4.A
【解析】由二次函数中,“当二次项系数为正时,图象开口向上,当二次项系数为负时,图象开口向下”结合“二次项系数的绝对值越大,图象的开口越大”分析可得:
.
故选A.
点睛:(1)二次函数的图象的开口方向由“的符号”确定,当时,图象的开口向上,当时,图象的开口向下;(2)二次函数的图象的开口大小由的大小确定,当越大时,图象的开口越小.
5.C
【解析】试题解析:∵抛物线y=3x2,
∴抛物线y=3x2的顶点坐标是:(0,0),
故选C.
6.D
【解析】
试题解析:∵将点P(1,-3)代入y=ax2得a=-3,
∴y=-3x2,
将四个点坐标分别代入解析式可知,当x=-1时,y=-3,即D选项正确,其他三个选项均不成立.
故选D.
7.D
【解析】解:∵函数y=2x2,y=x2,y=x2中,a取值范围分别为:a>0,a>0,a<0,∴抛物线的开口方向分别为:向上、向上、向下,即开口方向不同;
由函数y=2x2,y=x2,y=x2的解析式可知:顶点坐标都为(0,0);
∴他们共同的特点是都关于y轴对称,抛物线的顶点都是原点.
故选D.
8.A
【解析】函数的图象的对称轴是y轴,顶点是原点,开口向上,所以离原点越远,函数值就越大.
因为|-2|>1>0,所以y1>y3>y2.
故选A.
9.C
【解析】由a<-1可得a-1<a<a+1<0,又因点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2的图象上,在对称轴的左侧,y随x的增大而减小,所以 y3
【解析】A.在函数y=-x2中,当x=0时y有最大值0,正确,
因为:此抛物线顶点坐标在原点,开口方向向下,故当x=0时y有最大值0;
B.在函数y=2x2中,当x>0时y随x的增大而增大,正确;
因为此抛物线对称轴为y轴,开口方向向上,则x>0时y随x的增大而增大;
C.抛物线y=2x2,y=-x2,y=-x2中,抛物线y=2x2的开口最小,抛物线y=-x2的开口最大;错误;
根据绝对值越大开口越小,可得抛物线y=2x2的开口最小,抛物线y=-x2的开口最大;
D.不论a是正数还是负数,抛物线y=ax2的顶点都是坐标原点,正确,
因为y=ax2(a≠0)的顶点始终为原点.
【点睛】本题主要考查了二次函数的性质,解题的关键是熟练掌握顶点坐标,对称轴以及开口方向等知识,此题难度不大.
11.D
【解析】分析:分a<0和a>0两种情况,确定开口最小经过的点,代入解析式求出a的取值范围即可.
详解:若a<0,则抛物线开口向下,开口最小过点B(1,-1)
∴-1=a×12
∴a=-1
∴-1≤a<0
若a>0,则抛物线开口向上,开口最小过点A(1,2)
∴2=a×12
∴a=2
∴0
点睛:本题考查了二次函数的图象,有一定难度,进行分类讨论是解题的关键.
12.m<2
【解析】∵二次函数的图象开口向下,
∴m-2<0,解得:m<2.
故答案为:m<2.
13.y=2x2
【解析】图象的顶点在原点,开口向上的二次函数很多,如: .
14.①②④.
【解析】y=-2x2开口向下,对称轴是y轴,与x轴有一个交点,最高点是原点.
故答案为①②④.
点睛:掌握二次函数的图像及性质.
15. (0,0) y轴 ≤0 >0 0 小 0.
【解析】解:抛物线y=2x2的顶点,坐标为(0,0),对称轴是y轴.当x≤0时,y随x增大而减小;当x>0时,y随x增大而增大;当x=0时,y有最小值是0.
故答案为: (0,0) ; y轴 ; ≤0 ;>0 ; 0 ; 小; 0.
16.8
【解析】函数y=x2与y=–x2的图象关于x轴对称,又因正方形的边长为4,以正方形中心为原点建立平面直角坐标系,所以阴影部分的面积为正方形面积的一半,即4×4×=8.
点睛:本题考查了抛物线的性质,熟知与的图象关于x轴对称是解决问题的关键.
17.y=-3x2
【解析】把点A代入: 得, ,解得: ,
∴该抛物线的解析式为: .
18.②④
【解析】∵x2一定不小于0,则由条件“对应任意给定的x的值,都有y甲 y乙”可知:存在以下3种情况:
(1)若y甲和y乙都为正数,则m>0,n>0且m>n,即m>n>0;
(2)若y甲为正数,y乙为负数,则m>0,n<0;
(3)若都为负数时,则n<m<0;
∴关于m,n的关系正确的是② 、④ .
19.
【解析】当x=1时,y=x2=,则P1(1, ),所以S1=×1×=;
当x=2时,y=x2=2,则P2(2,2),所以S2=×1×(2-)= ;
当x=3时,y=x2=,则P3(3, ),所以S3=×1×(-2)=,
同样方法可得S4=,
所以Sn=.
故答案是: , .
【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了三角形面积公式.
20.(1)k=﹣3;(2)当k=﹣3时,y=﹣x2顶点坐标(0,0),对称轴为y轴,当x>0时,y随x的增大而减少.
【解析】试题分析:(1)根据二次函数的定义得出k2+k﹣4=2,再利用函数图象有最高点,得出k+2<0,即可得出k的值;
(2)利用(1)中k的值得出二次函数的解析式,利用形如y=ax2(a≠0)的二次函数顶点坐标为(0,0),对称轴是y轴即可得出答案.
试题解析:解:(1)∵是二次函数,∴k2+k﹣4=2且k+2≠0,解得k=﹣3或k=2.∵函数有最高点,∴抛物线的开口向下,∴k+2<0,解得k<﹣2,∴k=﹣3;
(2)当k=﹣3时,二次函数为y=﹣x2,顶点坐标为(0,0),对称轴为y轴,当x>0时,y随x的增大而减少.
21.(1)A点的坐标为:(2,4);(2)(2,0),(﹣2,0),(4,0),(5,0).
【解析】试题分析:(1)直接将A点代入解析式求出即可A点坐标即可;
(2)分别根据以O为顶点时,以A为顶点时,以P为顶点时求出符合题意的点的坐标即可.
试题解析:(1)∵点A(2,a)在抛物线y=x2上,∴a=22=4,
∴A点的坐标为:(2,4);
(2)如图所示:以O为顶点时,AO=P1O=2或AO=AP2=2
∴点P坐标:(2,0),(﹣2,0),以A为顶点时,AO=OP,
∴点P坐标:(4,0);以P为顶点时,OP′=AP′,
∴AE2+P′E2=P′A2,设AP′=x则42+(x﹣2)2=x2,解得:x=5,
∴点P坐标:(5,0),
综上所述使△OAP是等腰三角形则P点坐标为:(2,0),(﹣2,0),(4,0),(5,0).
22.(1)a=-1(2)y轴,(0,0)(3)图像见解析
【解析】试题分析:
(1)把点(1,b)代入y=2x-3中解得b的值,再把(1,b)代入y=ax2,中可解得a的值;
(2)由(1)中所求得的a的值,可得y=ax2的解析式,从而可确定抛物线y=ax2的开口方向,对称轴和顶点坐标;
(3)根据(2)中求得的抛物线y=ax2的开口方向、对称轴和顶点坐标可画出其草图.
试题解析:
(1)把(1,b)代入直线y=2x-3中,得b=2-3=-1,
把点(1,-1)代入y=ax2中,得a=-1;
(2)∵在y=-x2中,a=-1<0,
∴抛物线开口向下;
抛物线y=ax2的对称轴为y轴,顶点坐标为(0,0);
(3)作函数y=ax2的草图如下:
视频 ( http: / / qbm. / console / / media / Eav5S7TOlADNNq_QNVJsJ8azAU8bCp1TYsIBEk3JtT95_z9LGst1Vy9zKNNicDiideT_EHL6dJgUcbysgicX88dr8zlTjoBCtwREOpVZWepBuuU34LehdRLK01928wssd4PzhMfR9yrGqYq9wLNHJg )
23.见解析
【解析】试题分析:观察图像结合函数表达式可以得到两个函数开口向上,对称轴也都是y轴,顶点坐标分别是(0,0),(0,-1);根据二次函数的性质及图像知道抛物线y=x2-1与抛物线y=x2形状相同,对称轴相同,但是位置不同,开口方向也相同,所以可以得到抛物线y=x2-1可由抛物线y=x2向下平移1个单位长度得到的。
解:如图所示:
(1)抛物线y=x2开口向上,对称轴为y轴,顶点坐标(0,0);
抛物线y=x2-1开口向上,对称轴为y轴,顶点坐标(0,-1).
(2)抛物线y=x2-1可由抛物线y=x2向下平移1个单位长度得到.
24.(1) 3;(2) 27;(3)答案不唯一,
【解析】试题分析:抛物线y=ax2经过点(1,3),将点代入即可求得a=3,将x=3代入函数中求得y=27.二次函数的性质可以通过从开口方向,对称轴,顶点坐标,增减性等方面进行分析.
解:(1)∵抛物线y=ax2经过点(1,3),
∴a·1=3.∴a=3.
(2)把x=3代入抛物线y=3x2,得y=3×32=27.
(3)答案不唯一,如:抛物线的开口向上;坐标原点是抛物线的顶点;当x>0时,y随着x的增大而增大;抛物线的图象有最低点,当x=0时,y有最小值,是y=0等.
25.(1)y=﹣x+2,y=x2;(2)点C坐标为(﹣2,4);(3)3.
【解析】试题分析:(1)已知直线AB经过A(2,0),B(1,1),设直线表达式为y=kx+b,可求直线解析式;将B(1,1)代入抛物线y=ax2可求抛物线解析式;
(2)将(1)中所求的直线AB的解析式与抛物线y=ax2的解析式联立,得到方程组,解方程即可求出点C的坐标;
(3)已知A,B,C三点坐标,根据S△COB=S△AOC﹣S△OAB即可求△COB的面积.
试题解析:
(1)设直线表达式为y=kx+b.
∵A(2,0),B(1,1)都在y=kx+b的图象上,
∴,解得 ,,
∴直线AB的表达式为y=﹣x+2;
∵点B(1,1)在y=ax2的图象上,
∴a=1,其表达式为y=x2;
(2)由 ,解得 或,
∴点C坐标为(﹣2,4);
(3)S△COB=S△AOC﹣S△OAB=×2×4﹣×2×1=3.
【点睛】本题考查了二次函数的性质,利用待定系数法求一次函数、二次函数的解析式,三角形的面积.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
