第20章 数据的分析单元测试试题(含解析)
文档属性
| 名称 | 第20章 数据的分析单元测试试题(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 838.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-06-25 00:00:00 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
【人教版八年级数学(下)单元测试】
第二十章 数据的分析单元测试
(题数:28道 测试时间:90分钟 总分:120分)
班级:________ 姓名:________ 得分:________
一、单选题(每小题3分,共30分)
1.某市6月份某周气温(单位:℃)为23,25,28,25,28,31,28,这给数据的众数和中位数分别是( )
A.25,25 B.28,28 C.25,28 D.28,31
2.在统计中,样本的方差可以反映这组数据的( )
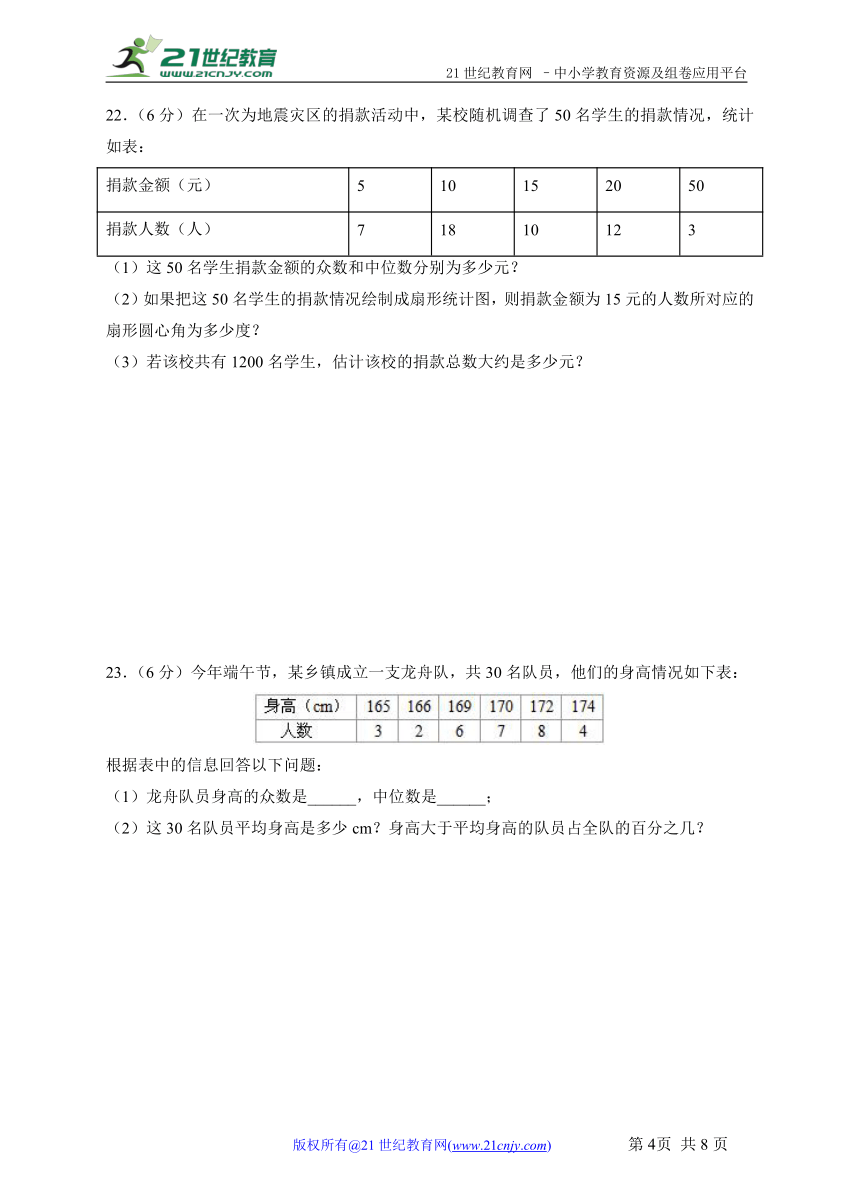
A.平均状态 B.分布规律 C.离散程度 D.数值大小
3.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这名同学成绩的( )
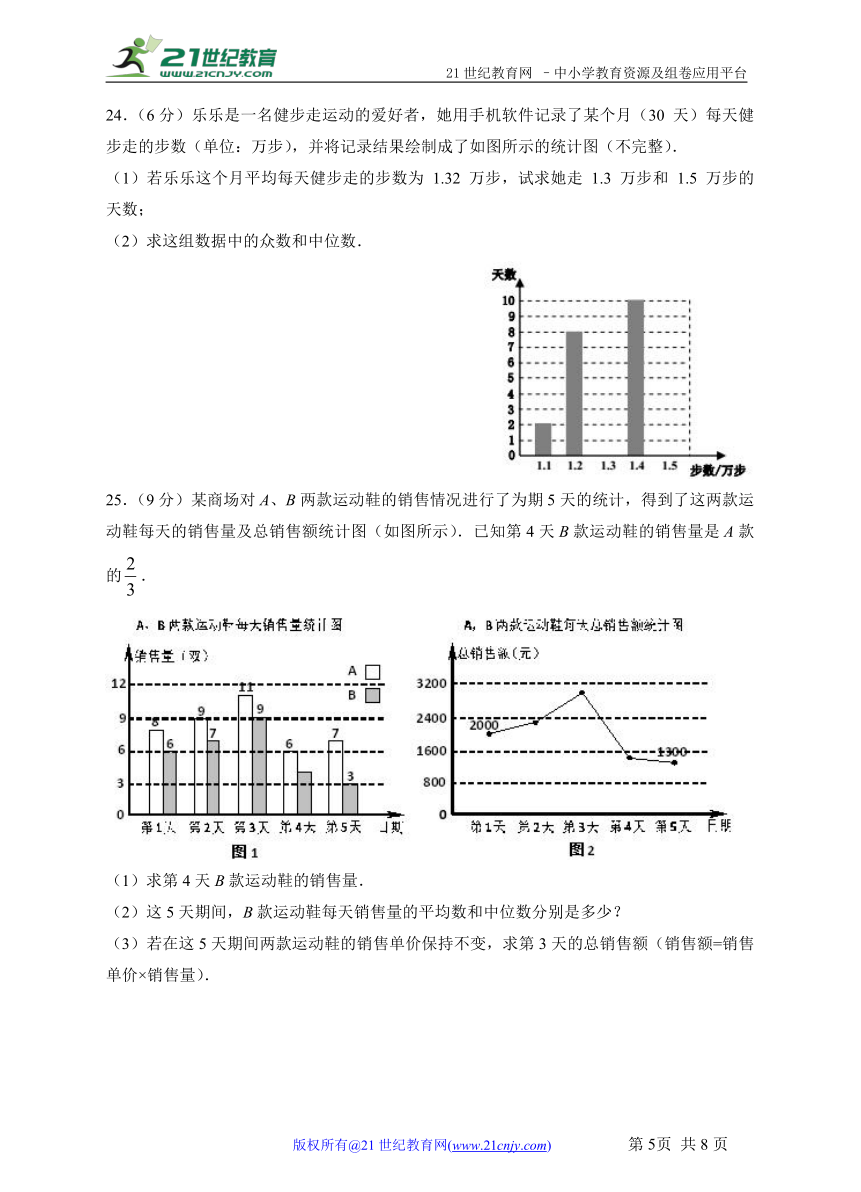
A. 众数 B. 中位数 C. 平均数 D. 方差
4.一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是( )
A. 6 B. 5 C. 4.5 D. 3.5
5.某班七个合作学习小组人数如下:4、5、5、x、6、7、8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.5 B.5.5 C.6 D.7
6.随着社会的进步,农村生活水平有了很大的提高,很多村寨都通上了自来水.为了解某组村民用水情况,随机抽取了八户家庭的月用水量,结果是(单位:吨):6,3,4,6,6,3,5,6.那么这组数据的众数是( )
A.3 B.4 C.5 D.6
7.商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如下表所示:
型号 22 22.5 23 23.5 24 24.5 25
数量(双) 2 6 11 15 7 3 4
经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
8.对于一组数据3,3,2,3,6,3,10,3,6,3,2:①众数是3;②众数与中位数的数值不等;③中位数与平均数的数值相等;④平均数与众数的数值相等,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
9.如果一组数据a1,a2,a3…,an方差是9,那么一组新数据a1+1,a2+1,a3+1…,an+1的方差是( )
A. 3 B. 9 C. 10 D. 81
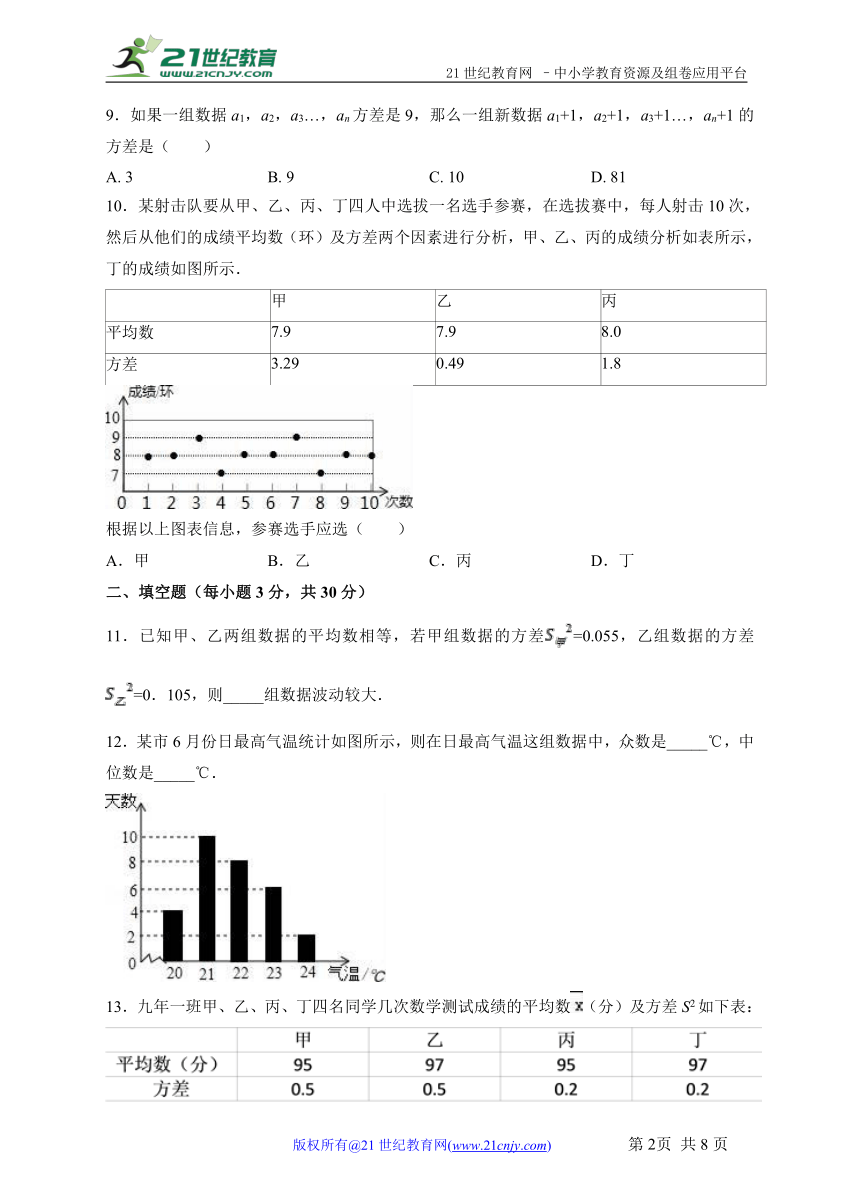
10.某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题3分,共30分)
11.已知甲、乙两组数据的平均数相等,若甲组数据的方差=0.055,乙组数据的方差=0.105,则_____组数据波动较大.
12.某市6月份日最高气温统计如图所示,则在日最高气温这组数据中,众数是_____℃,中位数是_____℃.
13.九年一班甲、乙、丙、丁四名同学几次数学测试成绩的平均数(分)及方差S2如下表:
老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选_____.
14.为了了解某小区居民的用水情况,随机抽查了该小区20户家庭的月用水量,数据见下表:
月用水量(m3) 8 9 10 11 12
户 数(个) 3 4 6 4 3
这20户家庭平均月用水量是 m3.
15.给出一组数据1,3,2,2,a,b,c,已知这组数据的众数为3,平均数为2,那么这组数据的方差为________.
16.一个样本的方差是,则这个样本的容量为___________,平均数为___________.
17.六个正整数的中位数是4.5,众数是7,极差是6,这六个正整数的和为________.
18.在一次学校的演讲比赛中,从演讲内容、演讲能力、演讲效果三个方面按照5:3:2计算选手的最终演讲成绩。已知选手甲演讲内容成绩为85、演讲能力成绩为90、演讲效果成绩
为95,那么选手甲的最终演讲成绩为 .
19.小明在一次考试中七科总分为638分,其中有两科的平均分是89分,那么另外五科的平均分是分_________.
20.甲、乙、丙三人的射击成绩如下图:三人中,________的射击成绩差,________更稳定.
三、解答题(共60分)
21.(6分)学生的平时作业、期中考试、期末考试三项成绩分别按2:3:5的比例计入学期总评成绩.小明、小亮、小红的平时作业、期中考试、期末考试的数学成绩如下表,计算这学期谁的数学总评成绩最高?
22.(6分)在一次为地震灾区的捐款活动中,某校随机调查了50名学生的捐款情况,统计如表:
捐款金额(元) 5 10 15 20 50
捐款人数(人) 7 18 10 12 3
(1)这50名学生捐款金额的众数和中位数分别为多少元?
(2)如果把这50名学生的捐款情况绘制成扇形统计图,则捐款金额为15元的人数所对应的扇形圆心角为多少度?
(3)若该校共有1200名学生,估计该校的捐款总数大约是多少元?
23.(6分)今年端午节,某乡镇成立一支龙舟队,共30名队员,他们的身高情况如下表:
根据表中的信息回答以下问题:
(1)龙舟队员身高的众数是______,中位数是______;
(2)这30名队员平均身高是多少cm?身高大于平均身高的队员占全队的百分之几?
24.(6分)乐乐是一名健步走运动的爱好者,她用手机软件记录了某个月(30 天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为 1.32 万步,试求她走 1.3 万步和 1.5 万步的天数;
(2)求这组数据中的众数和中位数.
25.(9分)某商场对A、B两款运动鞋的销售情况进行了为期5天的统计,得到了这两款运动鞋每天的销售量及总销售额统计图(如图所示).已知第4天B款运动鞋的销售量是A款的.
(1)求第4天B款运动鞋的销售量.
(2)这5天期间,B款运动鞋每天销售量的平均数和中位数分别是多少?
(3)若在这5天期间两款运动鞋的销售单价保持不变,求第3天的总销售额(销售额=销售单价×销售量).
26.(9分)某中学为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计(设每天的诵读时间为分钟),将调查统计的结果分为四个等级:Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
()请补全上面的条形图.
()所抽查学生“诵读经典”时间的中位数落在__________级.
()如果该校共有名学生,请你估计该校平均每天“诵读经典”的时间不低于分钟的学生约有多少人?
27.(9分)甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.
(1)请你根据图中的数据填写表格:
姓名 平均数 众数 方差
甲 8
乙 8 2.8
(2)从平均数和方差相结合看,分析谁的成绩好些?从发展趋势来看,谁的成绩好些.
28.(9分)某学校要成立一支由6名女生组成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:
平均数 标准差 中位数
甲队 1.72 0.038
乙队 0.025 1.70
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队中哪一队将被录取?请说明理由.
参考答案
1.B.
【解析】将这组数据从小到大的顺序排列23,25,25,28,28,28,31,
在这一组数据中28是出现次数最多的,故众数是28℃.
处于中间位置的那个数是28,那么由中位数的定义可知,这组数据的中位数是28℃;
故选B.
2.C
【解析】解:一般地设n个数据,x1,x2,…xn的平均数为,
则方差S2=[(x1-)2+(x2-)2+…+(xn-)2,
它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.而标准差是方差的算术平方根,
同样也反映了数据的波动情况.
故选C.
3.B
【解析】由于总共有7个人,且他们的分数互不相同,第4的成绩是中位数,要判断是否进入前4名,知道中位数即可判定.故选B.
4.C
【解析】若众数为1,则数据为1、1、5、7,此时中位数为3,不符合题意;
若众数为5,则数据为1、5、5、7,中位数为5,符合题意,
此时平均数为= 4.5;
若众数为7,则数据为1、5、7、7,中位数为6,不符合题意;
故选C.
5.C。
【解析】∵4、5、5、x、6、7、8的平均数是6,∴(4+5+5+x+6+7+8)÷7=6,解得:x=7。
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)。由此将这组数据重新排序为4、5、5、6、7、7、8,∴中位数是按从小到大排列后第4个数为:6。故选C。
6.D
【解析】本题考查统计的有关知识,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
解:在这一组数据中6是出现次数最多的,故众数是6.
故选D.
7.B
【解析】根据题意知:对商场经理来说,最有意义的是各种型号的运动鞋的销售数量,即众数.
故选B.
8.A
【解析】先把数据按大小排列,然后根据定义分别求出众数、中位数和平均数,最后逐一判断.
解:从小到大排列此数据为:2,2,3,3,3,3,3,3,6,6,10.
数据3出现了6次,最多,为众数;
第6位是3,3是中位数;
平均数为(2+2+3+3+3+3+3+3+6+6+10)÷11=4.
故选A.
9.B
【解析】解:设一组数据a1,a2,a3…,an平均数为a,∴一组新数据a1+1,a2+1,a3+1…,an+1的平均数为a+1,∵一组数据a1,a2,a3…,an方差是9,
∴ [(a1-a)2+(a2-a)2+(a3-a)2+…(an-a)2)]=9,
∴ [(a1+1-a-1)2+(a2+1-a-1)2+(a3+1-a-1)2+…(an+1-a-1)2)]
= [(a1-a)2+(a2-a)2+(a3-a)2+…(an-a)2)]
=9
故选B.
10.D.
【解析】观察图象可得丁射击10次的成绩为8、8、9、7、8、8、9、7、8、8,则丁的成绩的平均数为×(8+8+9+7+8+8+9+7+8+8)=8,方差为×[(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2]=0.4,比较可得丁的成绩的方差最小,即丁的成绩最稳定,所以参赛选手应选丁,故答案选D.
11.乙
【解析】∵S甲2<S乙2,
∴乙组数据波动较大.
故答案是:乙.
12. 21 22
【解析】由统计图可得出,该市6月份日最高气温为21℃的天数最多,
故这组数据中,众数为21℃,
将这组数据按照从小到大的顺序排列,可得出第15天和第16天的日最高气温均为22℃,
可得出中位数为: =22(℃).
故答案为:21,22.
13.丁.
【解析】由于乙的平均数较大且方差较小,故选丁.
故答案为丁.
14.10.
【解析】此题考查了加权平均数,掌握加权平均数的计算公式是解题的关键,是一道基础题.根据加权平均数的计算公式进行计算即可,把所有户的用水量加起来,再除以20,就得到这20户家庭的平均月用水量.
这20户家庭的平均月用水量是(8×3+9×4+10×6+11×4+12×3)÷20=10(m3).
故答案为10.
15.
【解析】因为众数为3,可设a=3,b=3,c未知,
平均数=(1+3+2+2+3+3+c)=2,
解得c=0,
将这组数据按从小到大的顺序排列:0、1、2、2、3、3、3,
∴
=
16.20;10
【解析】根据方差公式S2= [(x1-)2+(x2-)2+…+(xn-)2]中n表示样本容量,表示数据的平均数,故可知数据样本容量为20,平均数为10.
故答案为:20;10.
17.25或26或27
【解析】∵六个正整数,中位数是4.5,
∴第三个数与第四个数的和为9,且2 第三个数 4,
又∵众数是7,极差是6,
∴这六个正整数是:1、1、2、7、7、7,1、2、2、7、7、7,1、2、3、6、7、7,1、2、4、5、7、7,1、3、4、5、7、7,
∴这六个正整数的和为1+1+2+7+7+7=25,1+2+2+7+7+7=26,1+2+3+6+7+7=26,1+2+4+5+7+7=26,1+3+4+5+7+7=27.
故答案为25或26或27.
18.88.5
【解析】代入加权平均数公式计算即可得出结论.
解:该选手的综合成绩为:
85×5+90×3+95×2
5+3+2
=88.5.
故答案为:88.5.
19.92.
【解析】首先根据题意,用其中两科的平均分乘以2,求出它们的总分是多少,进而求出另外五科的总分是多少;然后根据平均数的求法,用另外五科的总分除以5,求出另外五科的平均分是多少即可.
(638﹣89×2)÷5=(638﹣178)÷5=460÷5=92(分)
∴另外五科的平均分是92分.
20.乙,丙.
【解析】根据图形可得:丙的成绩最差,乙的成绩波动最小,数据最稳定,
则三人中成绩最稳定的是乙,最差的是丙.
21.小亮成绩最高.
【解析】根据三项成绩比算出三个人的成绩,比较大小即可得出结果.
解:小明数学总评成绩:96×+94×+90×=92.4,
小亮数学总评成绩:90×+96×+93×=93.3,
小红数学总评成绩:90×+90×+96×=93.
∵93.3>93>92.4,∴小亮成绩最高.
答:这学期小亮的数学总评成绩最高.
22.(1)众数为10元,中位数为12.5元;(2)72°;(3)18120元
【解析】(1)由中位数、众数的定义即可得出答案;
(2)先求出捐款金额为15元的人数占50名学生的分率,再乘以360度即可;
(3)先求出样本平均数,再乘以1200即可估计出该校的捐款总数大约是多少元.
解:(1)根据表格可知这50名学生捐款金额的众数为10元,
又∵第25个数为10,第26个数为15,
∴中位数为=12.5元.
(2)由题意捐款金额为15元的人数所对应的扇形圆心角为360°×=72°.
(3)平均每人的捐款金额==15.1,
∴若该校共有1200名学生,估计该校的捐款总数大约是:15.1×1200=18120元.
23.(1)172cm;170cm;(2)170.1,40%.
【解析】(1)用众数和中位数的定义解答;
(2)用平均数的定义解答.
解:(1)172出现了6次,出现的次数最多,故众数是172(cm);
这组数据共30个,正中间两个是第15,16个,∴中位数为(170+170)÷2=170(cm);
(2)=170.1(cm),由表可知,身高大于平均身高的队员共有12人,占全队的百分比为=40%.
24.(1)6天,4天;(2)众数是1.4万步,中位数为1.3万步
【解析】(1)设乐乐有天每天走1.3万步,有天每天走1.5万步,
则
解得
即乐乐有6天每天走1.3万步,有4天每天走1.5万步.
(2)众数是1.4万步,中位数为1.3万步.
25.(1)4双;(2)6双;(3)2900元.
【解析】(1)由统计图可知第4天A款运动鞋销量是6双且B款运动鞋的销售量是A款的可得;
(2)根据平均数与中位数定义求解可得;
(3)设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为x元/双,根据第1天和第5天的总销售额列方程组求出A、B款运动鞋单价,即可得解.
解:(1)6×(双 )
∴第4天B款运动鞋的销售量是4双;
(2)B款运动鞋每天销售量的平均数为(双 ),
中位数为6 (双 )
(3)设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为y元/双.
由题意得: ,解得 ,
∴第3天的总销售额为(元)
26.()补全的条形图见解析()Ⅱ级.().
【解析】(1)根据Ⅱ级的人数和所占的百分比即可求出总数,从而求出三级人数,进而补全图形;
(2)把所有同类数据按照从小到大的顺序排列,中间的数据是中位数,则该数在Ⅱ级.;
(3)由样本估计总体,由于时间不低于的人数占,故该类学生约有408人.
解:(1)本次随机抽查的人数为:20÷40%=50(人).三级人数为:50-13-20-7=10.
补图如下:
(2)把所有同类数据按照从小到大的顺序排列,中间的数据是中位数,则该数在Ⅱ级.
(3)由样本估计总体,由于时间不低于的人数占,所以该类学生约有.
27.乙的成绩好些.
【解析】(1)直接结合图中数据结合平均数以及方差求法分别得出答案;
(2)利用方差反映数据稳定性平均数是反映整体的平均水平进而分析得出答案.
解:(1)如图所示:甲的平均数为:(7+8+9+8+8)=8,
= [(7﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2+(8﹣8)2]
=0.4;
由图中数据可得:乙组数据为8,
姓名 平均数 众数 方差
甲 8 8 0.4
乙 8 8 2.8
(2)从平均数和方差相结合看,甲的成绩好些,从发展趋势来看,乙的成绩好些.
28.(1)1.73米;(2)1.69, (3)乙队,理由:标准差小,数据波动小
【解析】(1)根据中位数的定义,把甲队队员身高从高到矮排列,找出位置处于中间的数即可;
(2)根据条形图可得到乙队队员每个人的身高,再用总身高÷队员人数=平均数身高;身高不小于1.70米的频率=身高不小于1.70米的人数÷乙队队员总数;
(3)根据标准差的意义可以得到答案;标准差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
解:(1)把甲队队员身高从高到矮排列:1.76,1.75,1.75,1.71,1.70,1.65,
位置处于中间的两数为:1.75,1.71,
故甲队身高的中位数是=1.73米;
(2)x乙=×(1.70+1.68+1.72+1.70+1.64+1.70)=1.69米,
故乙队身高的平均数是1.69米,
身高不低于1.70米的频率为 ;
(3)∵S乙<S甲,∴乙队的身高比较整齐,乙队将被录取.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com) 第2页 共8页
【人教版八年级数学(下)单元测试】
第二十章 数据的分析单元测试
(题数:28道 测试时间:90分钟 总分:120分)
班级:________ 姓名:________ 得分:________
一、单选题(每小题3分,共30分)
1.某市6月份某周气温(单位:℃)为23,25,28,25,28,31,28,这给数据的众数和中位数分别是( )
A.25,25 B.28,28 C.25,28 D.28,31
2.在统计中,样本的方差可以反映这组数据的( )
A.平均状态 B.分布规律 C.离散程度 D.数值大小
3.我市某中学举办了一次以“我的中国梦”为主题的演讲比赛,最后确定7名同学参加决赛,他们的决赛成绩各不相同,其中李华已经知道自己的成绩,但能否进前四名,他还必须清楚这名同学成绩的( )
A. 众数 B. 中位数 C. 平均数 D. 方差
4.一组数据1,5,7,x的众数与中位数相等,则这组数据的平均数是( )
A. 6 B. 5 C. 4.5 D. 3.5
5.某班七个合作学习小组人数如下:4、5、5、x、6、7、8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.5 B.5.5 C.6 D.7
6.随着社会的进步,农村生活水平有了很大的提高,很多村寨都通上了自来水.为了解某组村民用水情况,随机抽取了八户家庭的月用水量,结果是(单位:吨):6,3,4,6,6,3,5,6.那么这组数据的众数是( )
A.3 B.4 C.5 D.6
7.商厦信誉楼女鞋专柜试销一种新款女鞋,一个月内销售情况如下表所示:
型号 22 22.5 23 23.5 24 24.5 25
数量(双) 2 6 11 15 7 3 4
经理最关心的是,哪种型号的鞋销量最大.对他来说,下列统计量中最重要的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
8.对于一组数据3,3,2,3,6,3,10,3,6,3,2:①众数是3;②众数与中位数的数值不等;③中位数与平均数的数值相等;④平均数与众数的数值相等,其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
9.如果一组数据a1,a2,a3…,an方差是9,那么一组新数据a1+1,a2+1,a3+1…,an+1的方差是( )
A. 3 B. 9 C. 10 D. 81
10.某射击队要从甲、乙、丙、丁四人中选拔一名选手参赛,在选拔赛中,每人射击10次,然后从他们的成绩平均数(环)及方差两个因素进行分析,甲、乙、丙的成绩分析如表所示,丁的成绩如图所示.
甲 乙 丙
平均数 7.9 7.9 8.0
方差 3.29 0.49 1.8
根据以上图表信息,参赛选手应选( )
A.甲 B.乙 C.丙 D.丁
二、填空题(每小题3分,共30分)
11.已知甲、乙两组数据的平均数相等,若甲组数据的方差=0.055,乙组数据的方差=0.105,则_____组数据波动较大.
12.某市6月份日最高气温统计如图所示,则在日最高气温这组数据中,众数是_____℃,中位数是_____℃.
13.九年一班甲、乙、丙、丁四名同学几次数学测试成绩的平均数(分)及方差S2如下表:
老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选_____.
14.为了了解某小区居民的用水情况,随机抽查了该小区20户家庭的月用水量,数据见下表:
月用水量(m3) 8 9 10 11 12
户 数(个) 3 4 6 4 3
这20户家庭平均月用水量是 m3.
15.给出一组数据1,3,2,2,a,b,c,已知这组数据的众数为3,平均数为2,那么这组数据的方差为________.
16.一个样本的方差是,则这个样本的容量为___________,平均数为___________.
17.六个正整数的中位数是4.5,众数是7,极差是6,这六个正整数的和为________.
18.在一次学校的演讲比赛中,从演讲内容、演讲能力、演讲效果三个方面按照5:3:2计算选手的最终演讲成绩。已知选手甲演讲内容成绩为85、演讲能力成绩为90、演讲效果成绩
为95,那么选手甲的最终演讲成绩为 .
19.小明在一次考试中七科总分为638分,其中有两科的平均分是89分,那么另外五科的平均分是分_________.
20.甲、乙、丙三人的射击成绩如下图:三人中,________的射击成绩差,________更稳定.
三、解答题(共60分)
21.(6分)学生的平时作业、期中考试、期末考试三项成绩分别按2:3:5的比例计入学期总评成绩.小明、小亮、小红的平时作业、期中考试、期末考试的数学成绩如下表,计算这学期谁的数学总评成绩最高?
22.(6分)在一次为地震灾区的捐款活动中,某校随机调查了50名学生的捐款情况,统计如表:
捐款金额(元) 5 10 15 20 50
捐款人数(人) 7 18 10 12 3
(1)这50名学生捐款金额的众数和中位数分别为多少元?
(2)如果把这50名学生的捐款情况绘制成扇形统计图,则捐款金额为15元的人数所对应的扇形圆心角为多少度?
(3)若该校共有1200名学生,估计该校的捐款总数大约是多少元?
23.(6分)今年端午节,某乡镇成立一支龙舟队,共30名队员,他们的身高情况如下表:
根据表中的信息回答以下问题:
(1)龙舟队员身高的众数是______,中位数是______;
(2)这30名队员平均身高是多少cm?身高大于平均身高的队员占全队的百分之几?
24.(6分)乐乐是一名健步走运动的爱好者,她用手机软件记录了某个月(30 天)每天健步走的步数(单位:万步),并将记录结果绘制成了如图所示的统计图(不完整).
(1)若乐乐这个月平均每天健步走的步数为 1.32 万步,试求她走 1.3 万步和 1.5 万步的天数;
(2)求这组数据中的众数和中位数.
25.(9分)某商场对A、B两款运动鞋的销售情况进行了为期5天的统计,得到了这两款运动鞋每天的销售量及总销售额统计图(如图所示).已知第4天B款运动鞋的销售量是A款的.
(1)求第4天B款运动鞋的销售量.
(2)这5天期间,B款运动鞋每天销售量的平均数和中位数分别是多少?
(3)若在这5天期间两款运动鞋的销售单价保持不变,求第3天的总销售额(销售额=销售单价×销售量).
26.(9分)某中学为了解学生平均每天“诵读经典”的时间,在全校范围内随机抽查了部分学生进行调查统计(设每天的诵读时间为分钟),将调查统计的结果分为四个等级:Ⅰ级、Ⅱ级、Ⅲ级、Ⅳ级.将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
()请补全上面的条形图.
()所抽查学生“诵读经典”时间的中位数落在__________级.
()如果该校共有名学生,请你估计该校平均每天“诵读经典”的时间不低于分钟的学生约有多少人?
27.(9分)甲、乙两人参加学校组织的理化实验操作测试,近期的5次测试成绩如图所示.
(1)请你根据图中的数据填写表格:
姓名 平均数 众数 方差
甲 8
乙 8 2.8
(2)从平均数和方差相结合看,分析谁的成绩好些?从发展趋势来看,谁的成绩好些.
28.(9分)某学校要成立一支由6名女生组成的礼仪队,八年级两个班各选6名女生,分别组成甲队和乙队参加选拔.每位女生的身高统计如图,部分统计量如下表:
平均数 标准差 中位数
甲队 1.72 0.038
乙队 0.025 1.70
(1)求甲队身高的中位数;
(2)求乙队身高的平均数及身高不小于1.70米的频率;
(3)如果选拔的标准是身高越整齐越好,那么甲、乙两队中哪一队将被录取?请说明理由.
参考答案
1.B.
【解析】将这组数据从小到大的顺序排列23,25,25,28,28,28,31,
在这一组数据中28是出现次数最多的,故众数是28℃.
处于中间位置的那个数是28,那么由中位数的定义可知,这组数据的中位数是28℃;
故选B.
2.C
【解析】解:一般地设n个数据,x1,x2,…xn的平均数为,
则方差S2=[(x1-)2+(x2-)2+…+(xn-)2,
它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.而标准差是方差的算术平方根,
同样也反映了数据的波动情况.
故选C.
3.B
【解析】由于总共有7个人,且他们的分数互不相同,第4的成绩是中位数,要判断是否进入前4名,知道中位数即可判定.故选B.
4.C
【解析】若众数为1,则数据为1、1、5、7,此时中位数为3,不符合题意;
若众数为5,则数据为1、5、5、7,中位数为5,符合题意,
此时平均数为= 4.5;
若众数为7,则数据为1、5、7、7,中位数为6,不符合题意;
故选C.
5.C。
【解析】∵4、5、5、x、6、7、8的平均数是6,∴(4+5+5+x+6+7+8)÷7=6,解得:x=7。
中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数)。由此将这组数据重新排序为4、5、5、6、7、7、8,∴中位数是按从小到大排列后第4个数为:6。故选C。
6.D
【解析】本题考查统计的有关知识,众数是一组数据中出现次数最多的数据,注意众数可以不止一个.
解:在这一组数据中6是出现次数最多的,故众数是6.
故选D.
7.B
【解析】根据题意知:对商场经理来说,最有意义的是各种型号的运动鞋的销售数量,即众数.
故选B.
8.A
【解析】先把数据按大小排列,然后根据定义分别求出众数、中位数和平均数,最后逐一判断.
解:从小到大排列此数据为:2,2,3,3,3,3,3,3,6,6,10.
数据3出现了6次,最多,为众数;
第6位是3,3是中位数;
平均数为(2+2+3+3+3+3+3+3+6+6+10)÷11=4.
故选A.
9.B
【解析】解:设一组数据a1,a2,a3…,an平均数为a,∴一组新数据a1+1,a2+1,a3+1…,an+1的平均数为a+1,∵一组数据a1,a2,a3…,an方差是9,
∴ [(a1-a)2+(a2-a)2+(a3-a)2+…(an-a)2)]=9,
∴ [(a1+1-a-1)2+(a2+1-a-1)2+(a3+1-a-1)2+…(an+1-a-1)2)]
= [(a1-a)2+(a2-a)2+(a3-a)2+…(an-a)2)]
=9
故选B.
10.D.
【解析】观察图象可得丁射击10次的成绩为8、8、9、7、8、8、9、7、8、8,则丁的成绩的平均数为×(8+8+9+7+8+8+9+7+8+8)=8,方差为×[(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2+(8﹣9)2+(8﹣7)2+(8﹣8)2+(8﹣8)2]=0.4,比较可得丁的成绩的方差最小,即丁的成绩最稳定,所以参赛选手应选丁,故答案选D.
11.乙
【解析】∵S甲2<S乙2,
∴乙组数据波动较大.
故答案是:乙.
12. 21 22
【解析】由统计图可得出,该市6月份日最高气温为21℃的天数最多,
故这组数据中,众数为21℃,
将这组数据按照从小到大的顺序排列,可得出第15天和第16天的日最高气温均为22℃,
可得出中位数为: =22(℃).
故答案为:21,22.
13.丁.
【解析】由于乙的平均数较大且方差较小,故选丁.
故答案为丁.
14.10.
【解析】此题考查了加权平均数,掌握加权平均数的计算公式是解题的关键,是一道基础题.根据加权平均数的计算公式进行计算即可,把所有户的用水量加起来,再除以20,就得到这20户家庭的平均月用水量.
这20户家庭的平均月用水量是(8×3+9×4+10×6+11×4+12×3)÷20=10(m3).
故答案为10.
15.
【解析】因为众数为3,可设a=3,b=3,c未知,
平均数=(1+3+2+2+3+3+c)=2,
解得c=0,
将这组数据按从小到大的顺序排列:0、1、2、2、3、3、3,
∴
=
16.20;10
【解析】根据方差公式S2= [(x1-)2+(x2-)2+…+(xn-)2]中n表示样本容量,表示数据的平均数,故可知数据样本容量为20,平均数为10.
故答案为:20;10.
17.25或26或27
【解析】∵六个正整数,中位数是4.5,
∴第三个数与第四个数的和为9,且2 第三个数 4,
又∵众数是7,极差是6,
∴这六个正整数是:1、1、2、7、7、7,1、2、2、7、7、7,1、2、3、6、7、7,1、2、4、5、7、7,1、3、4、5、7、7,
∴这六个正整数的和为1+1+2+7+7+7=25,1+2+2+7+7+7=26,1+2+3+6+7+7=26,1+2+4+5+7+7=26,1+3+4+5+7+7=27.
故答案为25或26或27.
18.88.5
【解析】代入加权平均数公式计算即可得出结论.
解:该选手的综合成绩为:
85×5+90×3+95×2
5+3+2
=88.5.
故答案为:88.5.
19.92.
【解析】首先根据题意,用其中两科的平均分乘以2,求出它们的总分是多少,进而求出另外五科的总分是多少;然后根据平均数的求法,用另外五科的总分除以5,求出另外五科的平均分是多少即可.
(638﹣89×2)÷5=(638﹣178)÷5=460÷5=92(分)
∴另外五科的平均分是92分.
20.乙,丙.
【解析】根据图形可得:丙的成绩最差,乙的成绩波动最小,数据最稳定,
则三人中成绩最稳定的是乙,最差的是丙.
21.小亮成绩最高.
【解析】根据三项成绩比算出三个人的成绩,比较大小即可得出结果.
解:小明数学总评成绩:96×+94×+90×=92.4,
小亮数学总评成绩:90×+96×+93×=93.3,
小红数学总评成绩:90×+90×+96×=93.
∵93.3>93>92.4,∴小亮成绩最高.
答:这学期小亮的数学总评成绩最高.
22.(1)众数为10元,中位数为12.5元;(2)72°;(3)18120元
【解析】(1)由中位数、众数的定义即可得出答案;
(2)先求出捐款金额为15元的人数占50名学生的分率,再乘以360度即可;
(3)先求出样本平均数,再乘以1200即可估计出该校的捐款总数大约是多少元.
解:(1)根据表格可知这50名学生捐款金额的众数为10元,
又∵第25个数为10,第26个数为15,
∴中位数为=12.5元.
(2)由题意捐款金额为15元的人数所对应的扇形圆心角为360°×=72°.
(3)平均每人的捐款金额==15.1,
∴若该校共有1200名学生,估计该校的捐款总数大约是:15.1×1200=18120元.
23.(1)172cm;170cm;(2)170.1,40%.
【解析】(1)用众数和中位数的定义解答;
(2)用平均数的定义解答.
解:(1)172出现了6次,出现的次数最多,故众数是172(cm);
这组数据共30个,正中间两个是第15,16个,∴中位数为(170+170)÷2=170(cm);
(2)=170.1(cm),由表可知,身高大于平均身高的队员共有12人,占全队的百分比为=40%.
24.(1)6天,4天;(2)众数是1.4万步,中位数为1.3万步
【解析】(1)设乐乐有天每天走1.3万步,有天每天走1.5万步,
则
解得
即乐乐有6天每天走1.3万步,有4天每天走1.5万步.
(2)众数是1.4万步,中位数为1.3万步.
25.(1)4双;(2)6双;(3)2900元.
【解析】(1)由统计图可知第4天A款运动鞋销量是6双且B款运动鞋的销售量是A款的可得;
(2)根据平均数与中位数定义求解可得;
(3)设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为x元/双,根据第1天和第5天的总销售额列方程组求出A、B款运动鞋单价,即可得解.
解:(1)6×(双 )
∴第4天B款运动鞋的销售量是4双;
(2)B款运动鞋每天销售量的平均数为(双 ),
中位数为6 (双 )
(3)设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为y元/双.
由题意得: ,解得 ,
∴第3天的总销售额为(元)
26.()补全的条形图见解析()Ⅱ级.().
【解析】(1)根据Ⅱ级的人数和所占的百分比即可求出总数,从而求出三级人数,进而补全图形;
(2)把所有同类数据按照从小到大的顺序排列,中间的数据是中位数,则该数在Ⅱ级.;
(3)由样本估计总体,由于时间不低于的人数占,故该类学生约有408人.
解:(1)本次随机抽查的人数为:20÷40%=50(人).三级人数为:50-13-20-7=10.
补图如下:
(2)把所有同类数据按照从小到大的顺序排列,中间的数据是中位数,则该数在Ⅱ级.
(3)由样本估计总体,由于时间不低于的人数占,所以该类学生约有.
27.乙的成绩好些.
【解析】(1)直接结合图中数据结合平均数以及方差求法分别得出答案;
(2)利用方差反映数据稳定性平均数是反映整体的平均水平进而分析得出答案.
解:(1)如图所示:甲的平均数为:(7+8+9+8+8)=8,
= [(7﹣8)2+(8﹣8)2+(8﹣8)2+(9﹣8)2+(8﹣8)2]
=0.4;
由图中数据可得:乙组数据为8,
姓名 平均数 众数 方差
甲 8 8 0.4
乙 8 8 2.8
(2)从平均数和方差相结合看,甲的成绩好些,从发展趋势来看,乙的成绩好些.
28.(1)1.73米;(2)1.69, (3)乙队,理由:标准差小,数据波动小
【解析】(1)根据中位数的定义,把甲队队员身高从高到矮排列,找出位置处于中间的数即可;
(2)根据条形图可得到乙队队员每个人的身高,再用总身高÷队员人数=平均数身高;身高不小于1.70米的频率=身高不小于1.70米的人数÷乙队队员总数;
(3)根据标准差的意义可以得到答案;标准差越大,则平均值的离散程度越大,稳定性也越小;反之,则它与其平均值的离散程度越小,稳定性越好.
解:(1)把甲队队员身高从高到矮排列:1.76,1.75,1.75,1.71,1.70,1.65,
位置处于中间的两数为:1.75,1.71,
故甲队身高的中位数是=1.73米;
(2)x乙=×(1.70+1.68+1.72+1.70+1.64+1.70)=1.69米,
故乙队身高的平均数是1.69米,
身高不低于1.70米的频率为 ;
(3)∵S乙<S甲,∴乙队的身高比较整齐,乙队将被录取.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
版权所有@21世纪教育网(www.21cnjy.com) 第2页 共8页
